范文一:多边形的内角公式和多边形外角和的简单证明方法
多边形内角和定理证明
证法一:
在n边形内任取一点O,连结O与各个顶点,把n边形分成n个三角形.
因为这n个三角形的内角的和等于n·180°,以O为公共顶点的n个角的和是360°
所以n边形的内角和是n·180°-2×180°=(n-2)·180°.
即n边形的内角和等于(n-2)×180°.
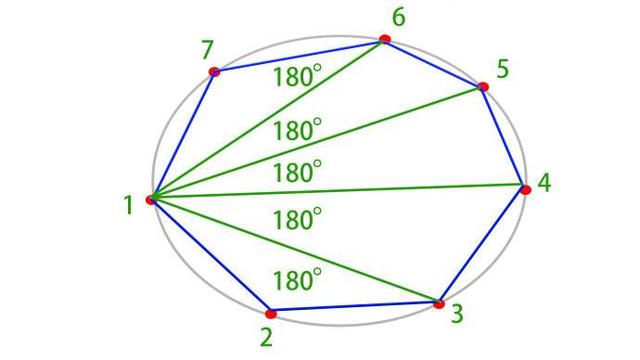
证法二:
连结多边形的任一顶点A1与其他各个顶点的线段,把n边形分成(n-2)个三角形.
因为这(n-2)个三角形的内角和都等于(n-2)·180°
所以n边形的内角和是(n-2)×180°.
证法三:
在n边形的任意一边上任取一点P,连结P点与其它各顶点的线段可以把n边形分成(n-1)个三角形,
这(n-1)个三角形的内角和等于(n-1)·180°
以P为公共顶点的(n-1)个角的和是180°
所以n边形的内角和是(n-1)·180°-180°=(n-2)·180°
多边形外角和证明
在多边形中每一个内角和与之相邻的外角都构成一个平角(180°),
那么:
n边形内角和+n边形外角和=n×180°
又∵多边形的内角和=(n-2)×180°
∴.n边形外角和= n×180°-(n-2)×180°
=360°
由此可见:任意多边形的外角之和都为360°
如三角形的外角和为360°、四边形的外角和也为360°,
即n边形的外角和与它的边的条数无关。
范文二:多边形的内角和
11.3.2 多边形的内角和
学习目标:
1.探索多边形的内角和公式及外角和。
2.会利用多边形的内角和公式解决问题。
学习重点:掌握多边形的内角和公式。
学习难点:探索多边形的内角和公式。
学习用具:三角尺
导学过程:
一:温故知新
1.多边形:。
2.三角形的内角和等于外角和等于。
3.长方形的内角和等于外角和等于。
4.从六边形的一个顶点出发可以画条对角线,这些对角线将六边
形分成 个三角形。
二:探究新知
1.任意四边形的内角和等于多少度?你是怎样得到的?
学习方法:独立思考1分钟后小组内交流答案。
2.探索同一种方法分别求出任意五边形、六边形的内角和等于多少
度?
学习方法:先独立思考2分钟,再小组进行讨论2分钟;看哪个
小组即对又快。
思考:通过上面的探索想一想,多边形的边数每增加一条,那么它的内角和就增加。
归纳总结一:多(n)边形的内角和公式: 。
3.把一个多边形分成几个三角形,还有其他分法吗?如果有,能得出多边形的内角和公式吗?以五边形为例证一证。
学习方法:先独立思考3分钟后,再小组长进行交流2分钟,最后进行小组讨论4分钟,然后展示交流自己的学习成果。
练习①你能说出七边形的内角和吗?十边形呢?
练习② 一个多边形的内角和等于1260°,那么它是几边形?
三:学以致用
1.在四边形ABCD中,∠A+∠C=180°,那么∠B+∠D等于多少
度?
2.根据前面三角形的有关知识,探索在每个五边形顶点处各取一
个外角,这些外角的和叫做五边形的外角和,请探究:
(1)五边形的外角和等于多少度?
(2)类似六边形的外角和是多少度?
归纳总结二:多(n)边形的外角和是: 。
四:总结与反思
请梳理一下,本节课你学到了哪些新知识?还有什么疑问需要交流?
五:展示平台
〈1〉基础巩固
①求下列图形中的x值
②一个多边形的内角和等于1800°,则它的边数为 条。
③已知四边形ABCD中,∠A∶∠B∶∠C ∶∠D=1∶2∶3∶4,则∠C= 。
④一个多边形的每个内角都等于150°,则它的边数为 条。
⑤正10边形的每个内角都等于 。
⑥如图,四边形ABCD中,∠A=∠C, ∠B=∠D,AB与CD有什么关系?请说明理由。
〈2〉创新思维
楠楠同学想设计一个内角和是2010°的多边形图案,他的想法能实现吗?试说明理由。
〈3〉中考链接
①若正多边形的一个外角是30°,则这是 边形。
②如图所示,小亮从A点出发前进10m,向右转15°,再前进10m,又向右转15°,……,这样一直走下去,他第一次回到出发点A时,一共走了 m。
范文三:《多边形的内角和
《多边形的内角和》教学设计郭礼 2011/9/23 15:07:40 石嘴山市第五中学 245 2
一、教材分析:
本节课是人教版《义务教育课程标准实验教科书》七年级《数学》下册第七章第三节《多边形的内角和》的第2课时,教材内容的安排先特殊后一般、由浅入深,渗透了转化的数学思想方法,符合学生认知规律,有利于培养学生的猜想、归纳能力及推理意识。具体来讲,在前一节学生已经学习了多边形及其对角线、内角、外角等概念,他们也熟知三角形和特殊四边形(如长方形、正方形)的内角和,所以这节课可以引导学生“将多边形分割成若干个三角形”来研究,体会转化思想在几何中的应用,感受从特殊到一般的认识问题的方法,体验解决问题策略的多样性,从而激发学生的学习兴趣,提高学生分析问题、解决问题的能力。 二、教学目标:
1.探索多边形内角和公式,并能应用之进行有关计算。
2.经历实验、猜想、推理、归纳等过程, 体会转化思想在几何中的运用,感受从特殊到一般的认识问题的方法。
3.通过探索多边形的内角和公式,尝试从不同角度解决问题的方法,从而提高学生分析、解决问题的能力。
三、教学重点、难点:
1.重点:探索多边形的内角和公式。 2.难点:如何将多边形转化成三角形。 四、学情分析及教学方法的选择
班级学生绝大部分数学基础和数学能力较差,教学中注重利用学生已有的知识经验,激励他们主动探究,在合作交流中逐步完善自己的想法并改进其做法,理解多边形内角和公式的由来。
五、教(学)具:三角尺、量角器等。 六、教学过程:
(一)新旧关联,导入新课
问题:三角形的内角和是多少度?长方形的内角和等于多少度?正方形的内角和等于多少度?
引出课题:想知道任意一个多边形的内角和吗?今天我们就来进一步探讨多边形的内角和。
(建立与学生的已有知识的联系,促使学生对新问题进行思考与猜想。) (二)新知探究与归纳
(从四边形到五边形、六边形至边形,增强图形的复杂性,经历转化的过程,让学生体会由简单到复杂、由特殊到一般的思想方法;同时在分组交流的过程中,感受合作的重要性。)
1.尝试探索特殊多边形的内角和
(1)任意四边形的内角和是多少度?用怎样的方法来说明?哪种方法最有说服力? (学生可能找到以下几种方法:量——即先测量四边形四个内角的度数,然后求四个内角的和;拼——即把四边形的四个内角剪下来,拼在一起,得到一个周角;分——即通过添加辅助线的方法,把四边形分割成三角形,此方法作为研究重点。)
(从四边形入手,让学生亲自操作、寻求结论,易于引起学习兴趣。鼓励学生寻求不同的方法,体验数学活动的乐趣及解决问题策略的多样性。)
(2)选一种你喜欢的“分割的方法”,求五边形、六边形的内角和。 2.探索多边形的内角和与边数间的关系
(1)可以要求学生完成以下表格:
(2)利用分割的方法,学生归纳总结得出
;
;
边形的内角和可能是以下不同形式:
。
(鼓励学生积极参与,合作交流, 尝试多种分割方式,领会转化的本质。通过多边形内角和的探索,体会数形间的联系,感受从特殊到一般的数学推理过程和数学思考方法。) (三)应用新知,尝试练习
(安排阶梯式的问题,通过练习来巩固新知识。备选题的目的是培养思维的灵活性,把握所学知识间的相互联系,让学生再次体会转化的思想方法。)
1.求课本83页练习1图(2)中的值。 2.已知一个多边形的每一个内角都等于150°,求这个多边形的内角和。(列方程求出边数,巩固多边形的内角和公式) 3.你能设计一个内角和是2010°的多边形图案吗? (引导学生利用多边形的内角和公式解释这种设想能否实现。)
4.(备选题)一个长方形截去一个角后,剩余部分的所有内角的和是多少度? (引导学生分析所有可能截取情况,根据不同截法得出不同结论。) (四)归纳总结
(鼓励学生畅所欲言,总结对本节课的收获和体会,培养归纳、总结的习惯和能力,自主建构知识体系。) (五)布置作业
(通过基础题目与课后练习来巩固知识、获得技能) 1.课本83页练习1、2;84——85页习题2、5。 2.“全品”练习册相应“课时作业”。
3.我们探索四边形的内角和时,曾使一个点在四边形的内部和边上运动,这个点能否冲破“禁区”运动到四边形的外部?请试一试。 附:板书设计
7.3.2多边形的内角和
四(五、六)边形的图形及其内角和度数 表格 —————— ———— 练习题—————————— 课后小记:
1.学生对“分割”的方法比较重视,能结合图形说理。课堂上把探索的主动权交给了学生,通过类比迁移,调动了学生认知的最近发展区。
2.学生对“备选题”非常感兴趣,他们动手尝试,观察、计算,产生了对数学知识的亲近感。
3. 有些学生解方程不够细心,应利用辅导课补习。
范文四:多边形的内角和
多边形的内角和
1. 计算:(1)10边形的内角和是多少?(2)2015边形的内角和与外角和各是多少?
巩固:一个多边形的内角和与外角和相加之后的结果为2520°,求这个多边形的边数。
2. 在四边形ABCD 中,∠A+∠C=216°,∠D=2∠B ,试求∠B 的度数和∠B 对应外角的度数。
B
巩固:在下面的五边形中,∠A=50°,∠B=125°,∠C=115°,∠D=150°,求∠DEA 的度数和与∠DEA 对应外角的度数。
D
A
3. 如图所示,已知∠A=25°,∠B=65°,∠D=30°,求∠1的度数。
D
巩固:求图中∠A 的度数。
4. 如图所示,求∠1+∠2+∠3+∠4+∠5+∠6。
巩固:求∠1+∠2+∠3的度数。
5. 如图,在四边形ABCD 中,DP ,CP 分别平分∠ADC 和∠BCD ,若∠A=110°,∠B=130°,那么∠P 的度数是
多少?
D
巩固:已知∠1=∠2,∠3=∠4,∠5=100°,求∠A 的度数。
B
6. 如图所示,已知ABCD 是正方形,三角形CDE 是等边三角形,求∠1的度数。
E
拓展
1. 如图,求∠1+∠2+∠3+∠4+∠5
2. 锐角△ABC 中,AD 和CE 分别是BC 和AB 边上的高,若AD 与CE 所夹的锐角是58°,则∠BAC+∠BCA 的大
小是多少?
3. 已知∠1=∠2=∠3,∠BAC=70°,求∠DEF 的度数。
B
C
4. 如图所示的六边形中,每个内角都是120°,其中四条边的长度分别是1,9,9,8厘米。这个六边形的周长
是多少厘米?
E
B
+
5. 九个同样的直角三角形卡片,拼成了如图所示的平面图形。这种三角形卡片中的两个锐角较小的一个是多
少度?
6. 如图,∠1+∠4=∠2+∠3,当∠AOB 是多少度时,图中所有角的内角和等于180°?
O
7. 如图,EF 是正方形ABCD 的对折线,将∠A 和∠B 的顶点重合于EF ,此时∠x 是多少度?
A
H E F
B
8. 圆周上有7个点A 1,A 2,?,A 7,以一笔画的方式将这7个点顺次连接成一个七角星的形状,则七角
星的七个“角”(是指圆周角)之和A 1+A 2+ +A 7是多少度?
范文五:多边形的内角和
. 7.3.2 多边形的内角和
西街中学 郭国伟 修改人:城北学校 马艳丽
学习目标:
1、通过多边形内角和与外角和计算公式的推导,培养自
己探索与归纳的能力。
2、会应用内角和与外角和公式进行有关计算。
学习重点难点:
重点:
多边形的内角和与外角和定理
难点:
多边形内角和以及外角和公式的推导
学法指导
能把多边形问题转化成三角形问题来解决。
考点剖析
本节内容在考试中多以计算题为主。
学习过程:
一. 知识链接,引入问题
我们知道三角形的内角和等于 , 正方形, 长方形的内角
和都等于 , 那么其他四边形的内角和等于多少?任意多边形的内角和又是多少?相信在本节课结束时, 会有一个满意的答案, 因此, 这节课我们一起探究多边形的内角和。
二 自主探究:(我会做下面的问题)
(一) 温故知新
1、n 边形的一个顶点可以引_____对角线。
将n 形分成了________个三角形
2、n 边形的对角线一共有______ 条。
(二) 探索新知:
(1) 自己任意画一个四边形, 量出它的4个内角, 计算他们
的和?再画几个四边形, 量一量, 算一算, 能得出什么结论?
(2)提出问题:
能否利用三角形内角和定理得出上述结论呢?
(3)画出任意一个四边形的一条对角线, 并观察这条对角线
能将这个四边形分成几个三角形?
(4)这样, 得出任意一个四边形的内角和都等于两个三角形
的内角和, 即等于 。
(5)归纳小结
从上面的问题, 我还能推出五边形内角和等于__
______,六边形的内角和等于。
(6)由此可以发现, 多边形的内角和与边数有关系.
一般地, 从n 边形的一个顶点出发, 可以引_________条对角
线, 它们将n 边形分成________个三角形, 则n 边形的内角和
等于____________。
定理:n边形内角和等于____________。
三 自主学习, 应用新知
例1 :如果一个四边形的一组对角互补, 那么另一组对角有什
么关系?
C
D
B
例2:如图, 在六边形的每个顶点处各取一个外角, 这些外角的和叫做六边形的外角和, 那么六边形的外角和等于多少?
结论:多边形的外角和等于____________。正n 边形每个外角度数为________________.
四 实践应用
1 十边形的内角和是___________。外角和是 2 如果一个多边形的内角和为540°,则这个多边形为
_________边形
3 一个多边形的内角和与它的一个外角的和为570°那么
这个多边形的边数为___________
4 过m 边形的一个顶点有7条对角线,n 边形没有对角线,则m+n= 。
5一个多边形的各个内角都等于120°那么这个多边形是 _______边形。
五 归纳梳理
1.这节课所学的内容:
2.我有何收获和疑问?
六 检查反馈
(一) 、选择题:
1.一个多边形的外角中, 钝角的个数不可能是( )
A.1个 B.2个 C.3个 D.4个
2.一个多边形的内角中, 锐角的个数最多有( )
A.3个 B.4个 C.5个 D.6个
3.四边形中, 如果有一组对角都是直角, 那么另一组对角可
能( )
A.都是钝角; B.都是锐角
C.是一个锐角、一个钝角 D.是一个锐角、一个直角
4.若从一个多边形的一个顶点出发, 最多可以引10条对角
线, 则它是( )
A.十三边形 B.十二边形 C.十一边形 D.十边形
5.若一个多边形共有十四条对角线, 则它是( )
A.六边形 B.七边形 C.八边形 D.九边形
(二) 、 判断题:
(1)当多边形的边数增加时,它的外角和也随着增加。 ( )
(2)正六边形的每个外角都等于60度。 ( ) (三 )、 填空
(1)正九边形的每一个外角都等于 度.
(2 )n 边形的每个内角都等于135°
则这个多边形是 边形.
(3)如果一个多边形 的内角和等于外角和
那么这个多边形是 边形。
七 巩固提高
1 、亮亮在求多边形的内角和时少算了一个角的度数,结果算出其余各内角和为2570°,请你帮助他计算出少算的这个角 的度数,并求这个多边形的边数?
八 课外作业(写到导学案)
课本:P85 习题7.3(5、 6, )
转载请注明出处范文大全网 » 多边形的内角公式和多边形外角



 夹了比嗨盗
夹了比嗨盗

