范文一:平面机构自由度计算
平面机构虚约束的分析
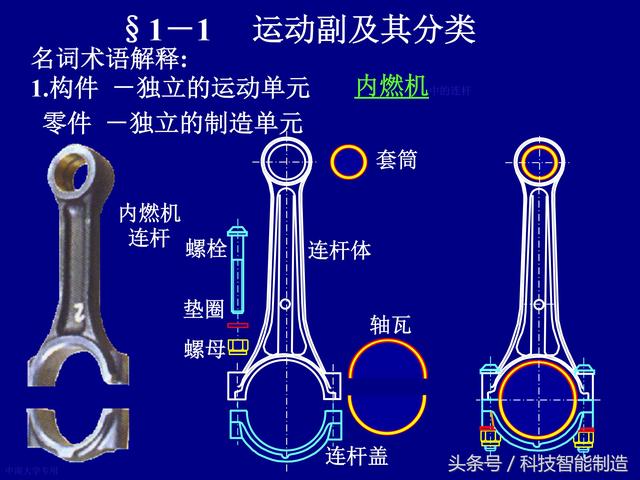
机构是由若干构件组成的,是实现机械预期运动的装置,这些“预期运动”都是在原动件的驱动下实现的,而其原动件的数目必须等于它的自由度。由此可见,准确计算机构的自由度对于正确分析和设计机构至关重要。在各种实际机构中,为了改善构件的受力情况,增
(1)加机构的刚度,或保证机构运动的顺利,往往要多增加一些构件与运动副这些运动副中往往包括虚约束。
(2)在计算平面机构自由度时,最常用的公式是契贝舍夫公式,简称契氏公式:
W=3n-2P-P LH
现计算下图所示机构的自由度:
可知,n=4, P=6, P=0, 所以W=3*4-2*6=0 LH
显然答案是错误的,原动件个数是1。这是因为该机构中出现了虚约束。所谓虚约束,笔者认为就是指不产生约束的约束,也即是所引入的构件由于几何尺寸满足一定的规律,不会对所在机构产生约束。
(3)在机构自由度计算中(产生虚约束的情况有4种情况:
(1)如果将机构的某个运动副拆开,机构被拆开的两部分在原联接点的运动轨迹仍相互重合,则产生虚约束。
(2)在机构运动过程中,如果某两构件上两点之间的距离始终保持不变(那么,若将此两点以构件相连,则因此而引入的约束必为虚约束。
(3)如果两构件在几处接触而构成移动副,且各接触处两构件的相对运动方向一致;或者两构件在几处配合而构成转动副,且各配合处的轴线重合,则只应考患一处运动副引入的约束,其他各处为虚约束。
(4)机构中对运动不起作用的对称部分亦是虚约束。
笔者认为,在分析机构是否含有虚约束时,最好的方法是先分析该构件的功能,特别是“可疑”构件的作用,然后试着去掉该构件,看该机构还能否实现所期待的功能,因为引入虚约束的目的是为了改善构件的受力情况,增加机构的刚度,或保证机构运动的顺利,且不影响机构的运动规律。例如以上机构的虚约束的作用是约束下面的导杆在水平方向运动,如
,,果去掉E,该机构的运动规律并没有发生改变,就可以断定E是虚约束。
在机械设计中,虚约束往往是“点睛之笔”,它能够使机械变得更加科学、实用。学会分析虚约束的最终目的是在自己设计机械机构的时候能够“因地适宜”、灵活地运用虚约束。
能否熟练实用虚约束是判断机械设计者是否合格的重要标准。
—————————————————————————————————————— 参考文献
(1)徐锦康(机械原理[M](北京:机械工业出版社
(2)李学荣(四连杆机构综合概论(第一册)[M](北京:机械工业出版 社。1985(
(3)孙桓,陈作模机械原理(第5版)[MJ北京:高等教育出
版社,1996(
电气工程及自动学院
胡佳男
范文二:平面机构自由度的计算
第九讲 平面机构自由度的计算
如 2— 18图所示, 作平面运动的刚体在空间的位置需要
三个独立的参数(x , y, θ)才能唯一确定。
1、单个自由构件的自由度为 3
2、构成运动副构件的自由度
如图 2— 19所示:
2— 18
图 2— 19运动副自由度 运动副 自由度数 约束数
回转副 1(θ) + 2(x , y ) =3
移动副 1(x ) + 2(y , θ) =3
高 副 2(x, θ) + 1(y ) =3
结论:构件自由度=3-约束数
3、机构的自由度
一个机构由 N 个构件组成,则活动构件有 n=N-1个
活动构件数 构件总自由度 低副约束数 高副约束数 n 3×n 2 × P L 1 × P h (低副数 ) (高副数 ) 计算公式: F=3n-(2PL +Ph )
计算图 2— 20中 1) 曲柄滑块机构的自由
度。
解:活动构件数 n=3
低副数 PL=4
高副数 PH=0
F=3n - 2PL - PH 图 2— 20曲柄滑块机构 =3×3 - 2×4
=1
2)计算图 2— 21中五杆铰链机构的自由度。
解:活动构件数 n=4
低副数 PL=5
高副数 PH=0
F=3n - 2PL - PH 图 2— 21五杆铰链机构
=3×4 -2×4
=2
3)计算图 2— 22中凸轮机构的自由度
解:活动构件数 n=2
低副数 PL=2
高副数 PH=1
F=3n -2PL -PH
=3×2 -2×2-1
=1 图 2— 22凸轮机构
范文三:平面机构自由度计算举例
平面机构自由度计算举例
例1计算如图所示机构的自由度,并判断它们是否具有确定的运动。(标有箭头的为原动件)
解:此轮系有两个行星轮2,其中一个为“对运动不起作用的对称部分”,则此行星轮及与其有关的一个回转副、两个高副引入一个虚约束。另外,轮5(系杆H)与机架在B和C处均构成回转副,可将B处的回转副视为虚约束;也可将C处的回转副视为虚约束,则B处为复合铰链。
活动构件数 n=5
低副数 P=5 L
高副数 P=4 H
故机构自由度为:
F=3n-2P-P=3×5-2×5-4,1 LH
由于自由度数F等于原动件数,故该机构有确定的运动。
例2 计算如图所示机构的自由度,并判断它们是否有确定的运动。
解 此机构A处为复合铰链。
活动构件数 n,10
低副数 P,14 L
高副数 P,0 H
故机构自由度为:
F,3n,2P,P,3×10,2×14,2 LH
由于自由度数F大于原动件数1,该机构没有确定的运动。如使之成为有确定的运动,需再有一个构件为原动件。
特例说明:如下图所示,不适用F,3n,2P,P公式。 LH
范文四:平面机构自由度的计算
平面机构自由度的计算
1、单个自由构件的自由度为 3
如所示,作平面运动的刚体在空间的位置需要三个独立的参
数(x,y, θ)才能唯一确定。
2、构成运动副构件的自由度
图2—19运动副自由度
运动副 自由度数 约束数
1(θ) + 2(x,y) =3 回转副
移动副 1(x) + 2(y,θ) =3
高 副 2(x,θ) + 1(y) =3
回转副
约束数为2 低副(面接触)
运
移动副 动 副 约束数为1 高副(点或线接触)
结论:构件自由度,3,约束数
3、平面机构的自由度
1)机构的自由度:机构中活动构件相对于机架所具有的独立运动的数目。
F,3n- 2P,P2).机构自由度计算公式 LH
式中: n-------活动构件数目(不包含机架)
P -----低副数目(回转副、移动副) L
P ------高副数目(点或线接触的) H
例题1: 计算曲柄滑块机构的自由度。
解:活动构件数n=3
低副数 PL=4
高副数 PH=0
F,3n- 2P,P 图 曲柄滑块机构 LH
=3×3 , 2×4
=1
例题2:计算五杆铰链机构的自由度。
解:活动构件数n=4
低副数 PL=5
高副数 PH=0
F,3n- 2P,P 图 五杆铰链机构 LH
=3×4 , 2×4
=2
例题3: 计算凸轮机构的自由度
解:活动构件数n=2
低副数 PL=2
高副数 PH=1
F,3n- 2P,P LH
=3×2 ,2×2,1
=1 图 凸轮机构
4(机构具有确定运动的条件
原动件的数目,机构的自由度数F(F,0或F?1)。
若 原动件数,自由度数,机构无确定运动;
原动件数,自由度数,机构在薄弱处损坏。
(a)两个自由度 (b)一个自由度 (c)0个自由度
图3-11 不同自由度机构的运动
5( 计算机构自由度时应注意的事项
1)复合铰链:两个以上个构件在同一条轴线上形成的转动副。
由m个构件组成的复合铰链,共有(m-1)个转动副。
Fnpp,3,2,lh
,3,5,2,7,0
,1
2)局部自由度:在某些机构中,不影响其他构件运动的自由度称为局部自由度
局部自由度处理:将滚子看成与从动杆焊死为一体。
注意:在去除滚子的同时,回转副也应同时去除,这就相当于使
机构的自由度数减少了一个,即消除了局部自由度。
3)虚约束:重复而不起独立限制作用的约束称为虚约束
计算机构的自由度时,虚约束应除去不计。
几种常见虚约束可以归纳为三类:
第一类虚约束:两构件之间形成多个运动副,它们可以是移动副(图2-17)或转动副(图2-18),这类虚约束的几何条件比较明显,计算自由度的处
理也较简单,两个构件之间只按形成一个运动副计算即可。
图3-14 导路重合的虚约束 图3-15 轴线重合的虚约束
第二类虚约束:机构中两构件上某两点的距离始终保持不变。如用一个附加杆件把这两点铰接,即形成虚约束。这两个点可以是某动点对某固定点的关系(如2-15
),也可以是两个动点之间的关系。这类虚约束常见于平行四边形机构,计中的E、F
算自由度时应撤去附加杆及其回转副。
第三类虚约束:机构中对运动不起作用的对称部分可产生虚约束(图2-19)。这类虚约束常见于多个行星齿轮的周转轮系,计算自由度时应只保留一个行星轮而撤去所有多余的行星轮及其有关运动副。
最后必须说明,虚约束是人们在工程实际中为改善机构或构件
受力状况,在一定条件下所采取的措施。在计算机构自由度时,
必须鉴别机构是否存在虚约束。为此,需要对机构的运动进行
分析,去除掉虚约束再进行计算。
例4 试计算图3-18a所示的大筛机构的自由度,并判断它是否有确定的运动。
a) b)
图3-18 大筛机构
解:机构中的滚子有一个局部自由度。顶杆与机架在E和E’组成两个导路平行的移动
副,其中之一为虚约束。C处是复合铰链。今将滚子与顶杆焊成一体,去掉移动
副E’,并在C点注明回转副的个数,如图3-18b)所示,由此得,n=7,P=9,L
P=1。其自由度为: H
F=3n-2P-P=3,7-2,9-1=2 LH
此机构自由度数等于2, 与原动件数相等,即W=F,机构具有确定的相对运动。
例5: 计算图3-17中,发动机配气机构的自由度。
解:此机构中,G,F为导路重合的两移动副,其中一个是虚约束;P处的滚子为
局部自由度。除去虚约束及局部自由度后,该机构则有n=6;P=8;P=1。LH
其自由度为:
F=3n-2P-P=3,6-2,8-1=1 LH
图3-17 发电机配气机构
例6:
练习:指出图3-20中运动机构的复合铰链、局部自由度和虚约束,并计算这些机构自由度,并判
断它们是否具有确定的运动(其中箭头所示的为原动件)。
范文五:第九讲 平面机构自由度的计算
如2—18图所示,作平面运动的刚体在空间的位置需要
三个独立的参数(x,y, θ)才能唯一确定。
1 3
2
如图2—19所示:
2—18
图2—19运动副自由度
运动副 自由度数 约束数
回转副 1(θ) + 2(x,y) =3
移动副 1(x) + 2(y,θ) =3
高 副 2(x,θ) + 1(y) =3
构件自由度=3-约束数
3
一个机构由N个构件组成,则活动构件有n=N-1个
活动构件数 构件总自由度 低副约束数 高副约束数
n 3×n 2 × P1× PL h
(低副数) (高副数)
F=3n(2P +P ) Lh
计算图2—20中1)曲柄滑块机构的自由
度。
解:活动构件数n=3
低副数 PL=4
高副数 PH=0
F=3n - 2PL - PH 图2—20曲柄滑块机构
=3×3 - 2×4
=1
2)计算图2—21中五杆铰链机构的自由度。
解:活动构件数n=4
低副数 PL=5
高副数 PH=0
F=3n - 2PL - PH 图2—21五杆铰链机构
3)计算图2—22中凸轮机构的自由度 =3×4 - 2×4
解:活动构件数n=2 =2
低副数 PL=2
高副数 PH=1
F=3n - 2PL - PH
=3×2 -2×2-1
=1 图2—22凸轮机构



 角落loser
角落loser

