范文一:3立体几何体积表面积公式
、考点梳理
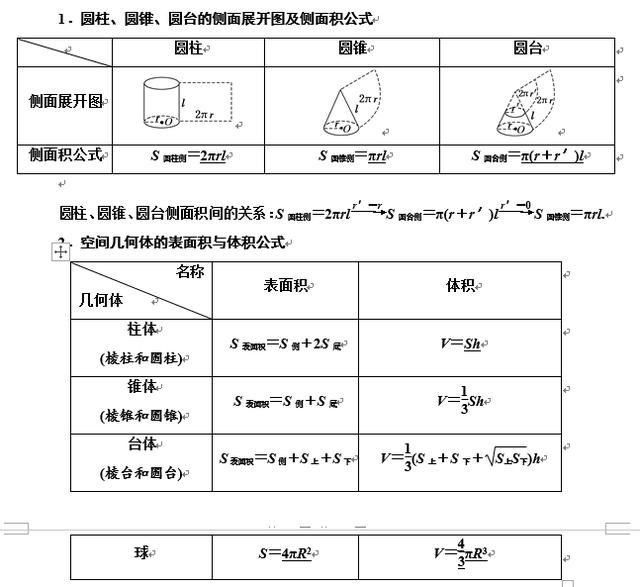
1(柱体、锥体、台体的侧面积就是各侧面面积之和,表面积是各个面的面积之和,即侧面积与底面积之和(
2r2(如果圆柱的底面半径是,母线长为,那么圆柱的底面积是, Sr,,l柱底
2Srl,2,Srrlrrl,,,,222(),,,圆柱的侧面积公式是,表面积是 ( 柱侧
r3(圆锥的侧面展开图是一个扇形(如果圆锥的底面半径是,母线长为,那么它的表l
2Srrlrrl,,,,,,,()面积是 (
4(圆台的侧面展开图是一个扇环,它的表面积等于上、下两个底面的面积和加上侧面
'22'Srrrlrl,,,,,()的面积,即(
5(棱柱和圆柱的体积公式为VShSh,()为底面面积,为高(
16(棱锥和圆锥的体积公式为( VShSh,()为底面面积,为高3
1'''SS,7(圆台和棱台的体积公式为,其中分别为上下底面面积,VSSSSh,,,()3
为圆台(棱台)的高( h
8(球的体积及球的表面积公式
43(1)如果球的半径为,那么它的体积为( ,,VRR3
2(2)如果球的半径为,那么它的表面积为( SR,4,R
三、知识精点讲解
1(多面体的面积和体积公式
名称 侧面积(S) 全面积(S) 体 积(V) 侧全
棱柱 直截面周长×l ?h=S?h S底直截面棱 S+2S 侧底柱 直棱柱 ch S?h 底
棱锥 各侧面积之和 1棱 S?h 1底S+S 侧底ch′ 锥 正棱锥 32
1棱台 各侧面面积之和 h(S+S上底下底S+S+S侧上底下棱 31台 (c+c′)h′ 正棱台 +) S,S 2底下底下底
表中S表示面积,c′、c分别表示上、下底面周长,h表斜高,h′表示斜高,l表示侧棱长。
2(旋转体的面积和体积公式
名称 圆柱 圆锥 圆台 球
2πrl πrl π(r+r)l S 12侧
22+r)l+π(r+r) π(r121222πr(l+r) πr(l+r) 4πR S 全
114222322πrh πh(r+rr+r) πR V πrh(即πrl) 1122333表中l、h分别表示母线、高,r表示圆柱、圆锥与球冠的底半径,r、r分别表示圆台 上、12下底面半径,R表示半径。
范文二:立体几何表面积公式总结
立体几何表面积公式总结
1 每份数×份数=总数
总数÷每份数=份数
总数÷份数=每份数
2 1倍数×倍数=几倍数
几倍数÷1倍数=倍数
几倍数÷倍数=1倍数
3 速度×时间=路程
路程÷速度=时间
路程÷时间=速度
4 单价×数量=总价
总价÷单价=数量
总价÷数量=单价
5 工作效率×工作时间=工作总量
工作总量÷工作效率=工作时间
工作总量÷工作时间=工作效率
6 加数+加数=和
和-一个加数=另一个加数
7 被减数-减数=差
被减数-差=减数
差+减数=被减数
8 因数×因数=积
积÷一个因数=另一个因数
9 被除数÷除数=商
被除数÷商=除数
商×除数=被除数
小学数学图形计算公式
1 正方形
C 周长 S 面积 a 边长
周长=边长×4
C=4a
面积=边长×边长
S=a×a
2 正方体
V:体积 a:棱长
表面积=棱长×棱长×6
S 表=a×a×6
体积=棱长×棱长×棱长
V=a×a×a
3 长方形
C 周长 S 面积 a 边长
周长=(长+宽)×2
C=2(a+b)
面积=长×宽
S=ab
4 长方体
V:体积 s:面积 a:长 b: 宽 h:高
(1)表面积(长×宽+长×高+宽×高)×2
S=2(ab+ah+bh)
(2)体积=长×宽×高
V=abh
5 三角形
s 面积 a 底 h 高
面积=底×高÷2
s=ah÷2
三角形高=面积 ×2÷底
三角形底=面积 ×2÷高
6 平行四边形
s 面积 a 底 h 高
面积=底×高
s=ah
7 梯形
s 面积 a 上底 b 下底 h 高
面积=(上底+下底)×高÷2
s=(a+b)× h÷2
8 圆形
S 面积 C 周长 ∏ d=直径 r=半径
(1)周长=直径×∏=2×∏×半径
C=∏d=2∏r
(2)面积=半径×半径×∏
9 圆柱体
v:体积 h:高 s; 底面积 r:底面半径 c:底面周长
(1)侧面积=底面周长×高
(2)表面积=侧面积+底面积×2
(3)体积=底面积×高
(4)体积=侧面积÷2×半径
10 圆锥体
v:体积 h:高 s; 底面积 r:底面半径
体积=底面积×高÷3
总数÷总份数=平均数
和差问题的公式
(和+差)÷2=大数
(和-差)÷2=小数
和倍问题
和÷(倍数-1) =小数
小数×倍数=大数
(或者 和-小数=大数)
差倍问题
差÷(倍数-1) =小数
小数×倍数=大数
(或 小数+差=大数)
植树问题
1 非封闭线路上的植树问题主要可分为以下三种情形: ⑴如果在非封闭线路的两端都要植树, 那么:
株数=段数+1=全长÷株距-1
全长=株距×(株数-1)
株距=全长÷(株数-1)
⑵如果在非封闭线路的一端要植树, 另一端不要植树, 那么: 株数=段数=全长÷株距
全长=株距×株数
株距=全长÷株数
⑶如果在非封闭线路的两端都不要植树, 那么:
株数=段数-1=全长÷株距-1
全长=株距×(株数+1)
株距=全长÷(株数+1)
2 封闭线路上的植树问题的数量关系如下
株数=段数=全长÷株距
全长=株距×株数
株距=全长÷株数
盈亏问题
(盈+亏)÷两次分配量之差=参加分配的份数
(大盈-小盈)÷两次分配量之差=参加分配的份数 (大亏-小亏)÷两次分配量之差=参加分配的份数 相遇问题
相遇路程=速度和×相遇时间
相遇时间=相遇路程÷速度和
速度和=相遇路程÷相遇时间
追及问题
追及距离=速度差×追及时间
追及时间=追及距离÷速度差
速度差=追及距离÷追及时间
流水问题
顺流速度=静水速度+水流速度
逆流速度=静水速度-水流速度
静水速度=(顺流速度+逆流速度)÷2
水流速度=(顺流速度-逆流速度)÷2
浓度问题
溶质的重量+溶剂的重量=溶液的重量
溶质的重量÷溶液的重量×100%=浓度
溶液的重量×浓度=溶质的重量
溶质的重量÷浓度=溶液的重量
利润与折扣问题
利润=售出价-成本
利润率=利润÷成本×100%=(售出价÷成本-1)×100% 涨跌金额=本金×涨跌百分比
折扣=实际售价÷原售价×100%(折扣<1)
利息=本金×利率×时间
税后利息=本金×利率×时间×(1-20%)
范文三:立体几何体积,表面积
立体几何表面积与体积
1、如图已知四棱锥P -ABCD 中的底面是边长为6的正方形,侧棱PA 的长为8,且垂直于底面,点M 、N 分别是DC 、AB 的中点.求
(1)异面直线PM 与CN 所成角的大小(结果用反三角函数值表示); (2)四棱锥P -ABCD 的表面积.
2、如图,四面体ABCD 中,O 、E 分别是BD 、BC 的中点,AO ⊥平面BCD ,
CA =CB =CD =BD =2.
(1)求三棱锥A -BCD 的体积;
(2)求异面直线AE 与CD 所成角的大小.
D
B
E
C
3、在正四棱锥P -ABCD 中,侧棱PA 的长为25,PA 与CD 所成的角的大小等于
. 5
D
(1)求正四棱锥P -ABCD 的体积;
(2)若正四棱锥P -ABCD 的五个顶点都在球O 的表面上,求此球O
的半径.
A
C
4、如图,直三棱柱ABC -A 1B 1C 1的体积为8,且AB =AC =2,∠BAC =90,E 是AA 1
的中点,O 是C 1B 1的中点. 求异面直线C 1E 与BO 所成角的大小.(结果用反三角函数值表示)
C1
B1
C1
B1
B
B
C
A
C
5、如图,△ABC 中,∠ACB =90,∠ABC =30 ,BC =
00
,在三角形内挖去一个
半圆(圆心O 在边BC 上,半圆与AC 、AB 分别相切于点C 、M ,与BC 交于点N ),将△ABC 绕直线BC 旋转一周得到一个旋转体。 (1)求该几何体中间一个空心球的表面积的大小; (2)求图中阴影部分绕直线BC 旋转一周所得旋转体的体积.
6、如图所示,在棱长为2的正方体ABCD -A 1B 1C 1D 1中,E , F 分别为线段DD 1, BD 的 中点.
(1)求三棱锥E -ADF 的体积; (2)求异面直线EF 与BC 所成的角.
A
F
C
A 1
E D 1
1
C 1
7、如图,在三棱锥P -ABC 中,PA ⊥底面ABC ,AC ⊥BC ,AC =BC =PA =2.
(1)求三棱锥P -ABC 的体积V ;
(2)求异面直线AB 与PC 所成角的大小. B
C
?
8、如图,直三棱柱ABC -A 1B 1C 1中,AB =AC =AA 1=2, ∠ABC =45.
(1)求直三棱柱ABC -A 1B 1C 1的体积;
(2)若D 是AC 的中点,求异面直线BD 与A 1C 所成的角.
C
B A 1
B
9、 如图,在三棱锥P -ABC 中,PA ⊥平面ABC ,AC ⊥AB ,AP =BC =4,
∠ABC =30?,
D 、E 分别是BC 、AP 的中点,
(1)求三棱锥P -ABC 的体积;
(2)若异面直线AB 与ED 所成角的大小为θ,求tan θ的值.
A
B
D
10、如图:已知AB ⊥平面BCD ,BC ⊥CD ,AD 与平面BCD 所成的角为30?,且
AB =BC =2.
(1)求AD 与平面ABC 所成角的大小; (2)求点B 到平面ACD 的距离.
C
11、长方体ABCD -A 1B 1C 1D 1中,底面ABCD 是正方形,AA 1=2, AB =1,E 是DD 1上的一点.
⑴求异面直线AC 与B 1D 所成的角;
⑵若B 1D ⊥平面ACE ,求三棱锥A -CDE 的体积;
A
D
12、如图,PA ⊥平面ABCD ,矩形ABCD 的边长AB =1,BC =2,E 为BC 的中点. (1)证明:PE ⊥DE ;
(2)如果PA =2,求异面直线AE 与PD 所成的角的大小. 解:(1)连AE ,由AB =BE =1,得AE =
2,同
D
13、 已知正四棱柱ABCD -A
1B 1C 1D 1的底面边长为2,A 1D =. (1)求该四棱柱的侧面积与体积;
(2)若E 为线段A 1D 的中点,求BE 与平面ABCD 所成角的大小.
C 1
A B 1
C
A B
14、在棱长为2的正方体ABCD -A 1B 1C 1D 1中,E , F 分别为A 1B 1, CD 的中点. (1)求直线EC 与平面B 1BCC 1所成角的大小; (2)求二面角E -AF -B 的大小.
15、如图,在直三棱柱ABC -A 1B 1C 1中,∠BAC =
π
2
,AB =AC =2,
C 1
AA 1=6,点E 、F 分别在棱AA 1、CC 1上,且AE =C 1F =2.
(1)求四棱锥B -AEFC 的体积;
(2)求?BEF 所在半平面与?ABC 所在半平面所成二面角θ的余弦值.
B
16、如图,已知正四棱柱ABCD -A 1B 1C 1D 1的底面边长是2,体积是16,M , N 分别是棱
BB 1、B 1C 1的中点.
(1)求直线MN 与平面ACC 1A 1所成的角(结果用反三角函数表示);
(2)求过A 1, B , C 1的平面与该正四棱柱所截得的多面体AC 11D 1-ABCD 的体积.
17、如图,正方体ABCD -A 1B 1C 1D 1的棱长为 (1)求直线DB 与平面A 1BCD 1所成角的大小; (2)求四棱锥D -BCD 1A 1的体积.
A
B
A A 1
18、如图,已知ABC -A 1B 1C 1是正三棱柱,它的底面边长和侧棱长都是2,D 为侧棱CC 1的中点.
BC 所成角的大小(结果用反三角函数值表示)(1)求异面直线A ; 1D 与
(2)求直线A 1B 1到平面DAB 的距离.
C 1
D
C
1
B
A 1
A
第21题图
19、已知正方体ABCD -A 1B 1C 1D 1,AA 1=2,E 为棱CC 1的中点.
(1)求异面直线AE 与DD 1所成角的大小(结果用反三角表示);
(2)求四面体AED 1D 的体积.
1
20、已知:四棱锥P -ABCD ,底面ABCD 是边长为2的菱形,PA ⊥平面ABCD ,且PA =2,∠ABC =60?,E ,F 分别是BC ,PC 的中点. (1)求四棱锥P -ABCD 的体积; P (2)求直线EF 与平面ABCD 所成角的大小.
F
A
C B E
21、如图,用半径为2cm ,面积为
D
2cm 2的扇形 铁皮制作一个无盖的圆锥形容器(衔接部分忽略不计),
该容器最多盛水多少?(结果精确到0.1 cm )
3
范文四:立体几何三视图体积表面积(学生)
立体几何三视图体积表面积
一、选择题
1.一个棱锥的三视图如图,则该棱锥的表面积为( )
(A
)48+(B
)48+(C
)72+(D
)72+2.某几何体的三视图如图所示,则该几何体的体积为( )
正视图 侧视图
俯视图
(A
)(B )4
3 (C )8
3 (D )4
3.一个几何体的三视图如图,则其体积为( )
A .20
3 B.6 C.16
3 D.5
4.一个四棱锥的三视图如图所示,其侧视图是等边三角形.该四棱锥的体积等于 (
)
A .3 B.23 C.3 D.63
5.某四面体的三视图如图所示,正视图、侧视图、俯视图都是边长为1的正方形,则此四面体的外接球的体积为 ( )
正视图 侧视图
俯视图
A .4ππ B. C .π D .3π 32
6.某三棱锥的三视图如图所示,该三棱锥的体积是为( )
A .80 B.40 C.8040 D. 33
7.某几何体的三视图如下图所示, 则该几何体的体积为
(A )200+9π
(B )200+18π
(C )140+9π
(D )140+18π
8.若某几何体的三视图如图所示,则此几何体的直观图是( )
侧(左)视图正视图
俯视图
A B C
9.某几何体的三视图如图所示,则该几何体的体积为
D
A .2π B.22π C.2ππ D. 33
10.如图所示是一个几何体的三视图,则这个几何体外接球的表面积为( )
A .8π B.16π C.32π D.64π
二、填空题
11.一个四棱柱的三视图如图所示,则其体积为_______.
12.若某几何体的三视图如右图所示,则此几何体的体积是______.
13.若某多面体的三视图如右图所示,则此多面体的体积为 ,外接球的表面积为 .
14.用18m 长的钢条围成一个长方体形状的框架,要求长方体的长与宽之比为2:1,则该长方体的最大体积是_____m .
15.一个球的内接圆锥的最大体积与这个球的体积之比为__________. 3
E 是BC 的16.如图,在正四棱柱(底面是正方形的直棱柱)ABCD A 1BC 11D 1中,
中点,F 是C 1D 的中点,P 是棱CC 1所在直线上的动点.则下列四个命题:
①CD ⊥PE
②EF //平面ABC 1
③V P -A 1DD 1=V D 1-ADE
④过P 可做直线与正四棱柱的各个面都成等角.
其中正确命题的序号是 (写出所有正确命题的序号).
三、解答题
17.如图所示,一圆柱内挖去一个圆锥,圆锥的顶点是圆柱底面的圆心,圆锥的底面是圆柱的另一个底面.圆锥的母线长为6,底面半径为2,求该几何体的表面积.
18.(本小题满分12分)已知某几何体的直观图和三视图如图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形.
(Ⅰ)若M 为CB 中点,证明:MA //平面CNB 1;
(Ⅱ)求这个几何体的体积.
19.(12分)如图,?
P 'AB
1的等边三角形,P 'C =P 'D =1现将?P 'CD 沿边CD 折起至PCD 得四棱锥P -ABCD , 且PC ⊥BC
P /
D C
A B A B
(1)证明:BD ⊥平面PAC ;
(2)求四棱锥P -ABCD 的体积.
20.(本小题满分12分)如图,在四棱锥P -ABCD 中,底面ABCD 为矩形,PA ⊥平面ABCD ,E 为PD 的中点. P
(1)求证:PB //平面AEC ;
(2)设PA =1, AB AD =2, 求三棱锥B -PCD 的体积。
21.(本小题满分12分)如图:三棱柱ABC -A 1B 1C 1中, 侧棱垂直底面, ∠ACB =90°,AC =BC=1AA 1,D 是侧棱AA 1的中点. 2
(Ⅰ)证明:平面BDC 1⊥平面BDC ;
(Ⅱ)平面BDC 1分此棱柱为两部分, 求这两部分体积的比.
22.(本小题满分13分)《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑. 在如图所示的阳马P -ABCD 中,侧棱PD ⊥底面ABC D ,且PD =CD ,点E 是PC 的中点,连接DE , BD , BE .
(Ⅰ)证明:DE ⊥平面PBC . 试判断四面体EBCD 是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,请说明理由;
V (Ⅱ)记阳马P -ABCD 的体积为V 1,四面体EBCD 的体积为V 2,求1的值. V 2
范文五:立体几何初步(表面积与体积)
立体几何初步(表面积与体积)
1、柱体、锥体、台体的表面积
注意:⑴几何体的表面积为几何体各个面的面积的和。
⑵特殊几何体表面积公式(c 为底面周长,h 为高,h 为斜高,l 为母线) ⑴S 直棱柱侧面积⑵S 圆柱侧
/
=ch
1ch ' 2
=2πrh
⑶S 正棱锥侧面积=⑷S 圆锥侧面积⑸S 正棱台侧面积=⑹S 圆台侧面积
=πrl
1
(c 1+c 2) h ' 2
=(r +R ) πl
⑺S 圆柱表=2πr (r +l ) ⑻S 圆锥表=πr (r +l ) ⑼S 圆台表=πr +rl +Rl +R ⑴V 柱=Sh
(
22
)
2、柱体、锥体、台体的体积公式
1
⑵V 锥=Sh
3
⑶V 台=(S ' S ) h
⑷V 圆台=
13
1' 1
(S +S ) h =π(r 2+rR +R 2) h 33
3、球体的表面积和体积公式 ⑴S 球=4πR ⑵V 球=
2
43 πR 3
巩固练习
1、一个圆柱的母线长为5,底面半径为2,则圆柱的轴截面的面积为( )
A 、10 B 、20 C 、40 D 、15
2、一个圆柱的轴截面面积为Q ,则它的侧面面积是 圆锥的侧面展开图扇形的圆心角为
3、球的体积与其表面积的数值相等,则球的半径等于( )
A .
1
B .1 C .2 D .3 2
1
B .1 2
C .2 D .3
4、两个球体积之和为12π,且这两个球大圆周长之和为6π,那么这两球半径之差是( )
A .
5、长方体ABCD -A 1B 1C 1D 1中,AB =3,AD =4,AA 1=5,则其外接球的体积为6、直径为10cm 的一个大金属球,熔化后铸成若干个直径为2cm 的削球,如果不计损耗,可铸成这样的
小球的个数为( )
A .5 B .15 C .25 D .125 7、与正方体各面都相切的球,它的表面积与正方体的表面积之比为( )
A .
ππππ
B . C . D . 2643
1
,求截面面积。 6
8、圆锥底面半径是6,轴截面顶角是直角,过两条母线的截面截去底面圆周的9、若正棱锥的底面边长与侧棱长相等,则该棱锥一定不是( ) A 、 三棱锥 B 、 四棱锥 C 、 五棱锥 D 、 六棱锥
10、球的表面积扩大为原来的4倍,则它的体积扩大为原来的___________倍
11、长方体的三个相邻面的面积分别为2,3,6,这个长方体的顶点都在同一个球面上,
则这个球的面积为 ( )
A.
7
π B.56π C.14π D.64π 2
12、求棱长为1的正四面体的外接球、内切球的表面积.
13、若圆锥的侧面面积是其底面面积的2倍,则这个圆锥的母线与底面所成的角为
14、一个球与它的外切圆柱、外切等边圆锥(圆锥的轴截面为正三角形)的体积之比( )
A .2:3:5 B .2:3:4 C .3:5:8 D .4:6:9
15、长方体AC 1的长、宽、高分别为3、2、1,从A 到C 1沿长方体的表面的最短距离为( ) A . 1+ B . 2+ C . 32 D . 23
16、在正三棱柱P -ABC 中,侧面为顶角为40,腰长为2的等腰三角形,已知点M 、N 分别在线段PB 、
PC 上运动,求AM+MN+NA的最小值
17、设正三棱锥P -ABC 的侧棱长为l ,∠APB=
周长的最小值
18、中心角为135°的扇形,其面积为B ,其围成的圆锥的全面积为A ,则A :B 为( ) A .11:8 B .3:8 C .8:3 D .13:8 19、正六棱锥的高为4cm ,最长的对角线为43cm ,则它的侧面积为_________
π
,且E 、F 分别是BP ,CP 上的点,求△AEF 6
20、已知正三棱锥的侧面积为183cm ,高为3cm 。求它的体积 21、一个与球心距离为1的平面截球体所得的圆面面积为π,则球的体积为 ( )
82π8π32πA . B . C . D .8π
333
22、圆锥的全面积为15π cm 2,侧面展开图的圆心角为60°,则该圆锥的体积为________cm3
6
23、若一个底面边长为6的正六棱柱的所有顶点都在一个球面上,求该球的体积和表面积.
2
24、以三棱锥各面重心为顶点,得到一个新三棱锥,它的表面积是原三棱锥表面积的( )
2
1111 B. C. D. 3491625、有棱长为6的正四面体S-ABC ,A 1、B 1,SB ,SC 上,且SA SB 1=3,SC 1=4,C 1分别在棱SA ,1=2,则截面A 'B 'C '将此正四面体分成的两部分体积之比为( ) 1111 A. B. C. D.
9843
A.
26、长方体的全面积是11,十二条棱长的和是24,则它的一条对角线长是( )
A .23 B . C . 5 D . 6
27、已知正四面体A-BCD 的表面积为S ,其四个面的中心分别为E 、F 、G 、H ,设四面体E-FGH 的表面积为
T
等于( ) S 1411 A . B . C . D .
9394
28、把直径分别为6cm , 8cm , 10cm 的三个铁球熔成一个大铁球,这个大铁球的半径是( ) A .3cm B . 6cm C . 8cm D . 12cm
T ,则
29、棱台的上、下底面面积分别为4和9,则这个棱台的高和截得棱台的原棱锥的高的比是( ) A .
1123 B . C . D .
3234
30、一个四面体的所有棱长都为2,四个顶点在同一个球面上,则此球的表面积为31、一个圆锥的侧面积是底面积的2倍,则圆锥侧面展开图扇形的圆心角度数为( )
A . 120? B . 180? C . 240? D . 300?
32、一个圆锥的高是10cm ,侧面展开图是半圆,求圆锥的侧面积
33、若圆锥的侧面展开图是圆心角为120?、半径为l 的扇形,则这个圆锥的表面积与侧面积的比是( )
A . 3:2 B . 2:1 C . 4:3 D . 5:3
34、如图:直三棱柱ABC —A 1B 1C 1的体积为V ,点P 、Q 分别在侧棱AA 1和CC 1上,AP=C1Q ,则四棱锥B —APQC
的体积为 ( )
V V
A. B. P
23
A'
C'
Q C V V
C. D. 45
A
35
、个长方体的某3
则这个长方体的体积是
36、设等边三角形△ABC 的边长为a ,P 是△ABC 内的任意一点,且P 到三边AB ,BC ,CA 的距离分别;由以上平面图形的特性类比空间图形:设正四面体ABCD 的棱长为a ,P 是正四面体ABCD 内的任意一点,且P 到四个面的距离分别为d 1,d 2,d 3,d 4,则有d 1+d 2+d 3+d 4为定值是 、
为d 1,d 2,d 3,则有d 1+d 2+
d 3
37、如左下图,在长方体ABCD -A 1B 1C 1D 1中,如果分别过BC 、A 1D 1的2个平行平面将长方体分成体积相等的3部分,那么
1
C 1N
=ND 1
C 1
D a A M
b
D C A B
38、如右上图,已知底面半径为r 的圆柱被一个平面所截,剩下部分母线长的最大值为a ,最小值为b ,那么圆柱被截后剩下部分的体积是 .
39、三个球的半径R 1, R 2, R 3,满足R 1+2R 2=3R 3,则它们的表面积S 1, S 2, S 3,满足的关系是40、已知半径是13的球面上有A 、B 、C 三点,AB=6 ,BC=8, AC=10;则球心O 到截面ABC 的距离为( )
A .12 B .8 C .6 D .5 41、如图,在多面体ABCDEF 中,已知ABCD 是边长为1的正方形,且?ADE 、?BCF 均为正三角形,EF ∥AB ,EF=2,则该多面体的体积为
23 B . 3343 C . D .
32
A .
42、如图,一个底面半径为R 的圆柱形量杯中装有适量的水, 若放入一个半径为r 的实心铁球,水面高度
恰好升高r ,则
R
r
43、已知过球面上A , B , C 三点的截面和球心的距离为球半径的一半,且AB =BC =CA =2,求球的表面积。
44、如图所示,球面上有四个点P 、A 、B 、C ,如果PA ,PB ,PC 两两互相垂直,且PA=PB=PC=a ,求这
个球的表面积。
45、⑴我国首都靠近径大约为6370km )
⑵在半径为13cm 的球面上有A , B , C 三点,AB =BC =AC =12cm ,求球心到经过这三点的截面的距离。
46、在北纬45圈上有A , B 两点,设该纬度圈上A , B
两点的劣弧长为
北纬60纬线,求北纬60纬线的长度等于多少km ?(地球半
00
,求A , B R (R 为地球半径)
4
两点间的球面距离。
47、已知:一个圆锥的底面半径为R ,高为H ,在其中有一个高为x 的内接圆柱. ⑴求圆柱的侧面积;
⑵x 为何值时,圆柱的侧面积最大.
48、如图,一个倒圆锥形容器,它的轴截面是正三角形,在容器内放一个半径为r 的铁球,并向容器内注
水,使水面恰在此时好与铁球相切,将球取出后,容器内的水深是多少?
转载请注明出处范文大全网 » 3立体几何体积表面积公式



 跋涉千里向你道别
跋涉千里向你道别

