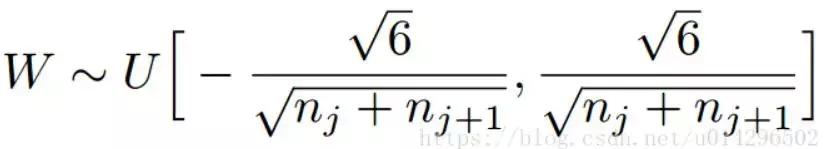
范文一:几种常见的概率分布
几种常见的概率分布 一、 离散型概率分布
1. 二项分布
n次独立的贝努利实验,其实验结果的分布(一种结果出现x次的概率是多少的分布)即为二项分布
应用二项分布的重要条件是:每一种实验结果在每次实验中都有恒定的概率,各实验之间是重复独立的
平均数: ,,,E(Y)npX
2,,,np(1p),,,npP(1)方差与标准差: ; XX
特例:(0-1)分布
若随机变量X的分布律为
kk1,p(xk)p(1p),,, k=0,1;0<><1, 则称x服从参数p的(0-1)分布="">
2. 泊松分布
泊松分布是一种用来描述一定的空间和时间里稀有事件发生次数的概率分布
泊松分布变量x只取零和正整数:0、1、2…..其概率函数为:
x,,,pe(x),
x!
泊松分布的平均数: ,,,,E(x)
2,,,,,,泊松分布的方差和标准差: 、
3. 超几何分布
knk,CCMNM,P(X=k)= 记X~(N,M,n) nCN
MP= N
期望:E(X)=np
Nn,方差:D(X)=np(1-p) N,1
适用范围:多次完全相同并且相互独立的重复试验,如果在有限总体中不重
复抽样,抽样成功的次数X的概率分布服从超几何分布,如福利彩票 二、 连续型概率分布
1. 均匀分布
若随机变量X具有概率密度函数
1,,;axb,, ,f(x),ba,,
,0,其他 ,
则称X在区间(a,b)上服从均匀分布,记为X U(a,b) ~在区间(a,b)上服从均匀分布的随机变量X的分布函数为
0,xa,,xa,, F(x),,,,axb,ba,,bx,1,,
2指数分布
,,x,,ex,0,
f(x),,,0若随机变量X具有概率密度函数 其中 是常数, ,0,0x,,
,则称X服从以 为参数的指数分布,记作 ,X的分布函数为 XE~(),
,,x,1,0,,ex
F(x), ,0,0x,,
3.正态分布
正态随机变量X的概率密度函数的形式如下:
2(x),,,122, ,,,,,,fex(x),
,,2
2,,式中, 为随机变量X的均值; 为随机变量X的方差。
22,,,,通常对具有均值,方差为的正态概率分布,记为N(,)。于是有正态
2,,随机变量X~N(,)。
24. 分布 ,
如果从标准正态分布N(0,1)的总体中得到n个随机变量分别为 XXX,....,,12n
222时,则由 得到的分布叫做自由度为n的 分布,记为 X,X~n,(),i
2 。 X~n,()
2分布的数学期望和方差分别为: ,
E(X)= n,D(X)=2n
2关于分布的加法定理。设,是相互独立的随机变量,且XXX,....,,12k
2 Xk~(n),i1,2,....,,,则ii
k2 X~(nn...n),,,,12ik
,1i
2分布与N(0,1)分布有如下关系: ,
是相互独立的随机变量,并且 ~(0,1),i=1,2,…n,则 设XXX,....,X12nin22X~(n), ,i
,1i
5.t分布
2设X~N(0,1), ,X与Y相互独立,则随机变量 Y~(n),
Xt,
Yn/
X遵从n个自由度的t分布,记为。 tt,~(n)
Yn/t分布的数学期望和方差如下:
n当n>2时,E(t)=0,D(t)= n,2
t分布的图形是对称的。当n<>
n,,密度函数曲线比较平缓,随着n的增大,t分布逐渐逼近标准正态分布。当
时,t分布渐近标准正态分布。
6.F分布
22X~(n),Y~(n),设随机变量 ,,且X与Y相互独立,则称随机变量 12
Xn/1 F,
Yn/2
遵从自由度为 的F分布,记作F~F (n,n)(n,n)1212
F分布的形状为正偏态分布状,但随着的增大,其概率密度曲线的偏n,n12
斜度虽有所缓减却仍保持偏态分布,并不以正态分布为其极限分布形式。
2如果 ,则 tt~(n)tF~(1,n)
1如果 。 F~F(n,n),~F则(n,n)1221F
范文二:几种常见的概率分布
几种常见的概率分布
几种常见的概率分布
1.概述
2.概率计算
3.实例分析
本章小结
概述
统计推断的理论基础是概率与概率分布。
概率分布是由随机变量的各数值和其概率组成。
概率
概率是对随机事件发生可能性大小的测定。频率与概率都是介于,与,之间的分数,当被研究对象是总体的全部单位时,频率就是概率;当被研究对象是总体的部分单位时,频率就只是试验概率;当试验次数或抽样次数非常大时,频率逼近概率。
概率分布
概率分布是由随机变量的各数值和其概率所组成,次数分布是由各组变量值和各组变量出现的次数所组成。次数分布是把某个试验中确实发生的全部结果的观察次数加以排列,而概率分布则是把全部可能试验的全部可能结果的概率加以排列;次数分布随样本不同而不同,概率分布却是唯一的。所以概率分布是理论上的次数分布,是对随机变量分布规律的描述。
随机变量及分布
离散、连续随机变量
如果随机变量X的可能取值都能一一列举出来,则称X为离散型随机变量。
如果随机变量X的所有可能取值不能一一列举出来,则称X为非离散型随机
变量,其中最常遇到的非离散型随机变量是连续型随机变量。
常见分布
常见的离散变量概率分布:0—1分布、二项分布、超几何分布、几何分布、
普阿松分布
常见的连续变量概率分布:均匀分布、正态分布、指数分布 概率计算
Transform
??compute 出现对话框
离散型随机变量
连续型随机变量
对话框
常见离散变量概率分布
二项分布
泊松分布
超几何分布
例子:二项分布
连续变量概率分布
均匀分布
正态分布
指数分布
例子:正态分布
实例分析
1.击中目标次数的概率分布
2.不合格产品的概率分布
3.交通事故的发生概率
4.金属棒长度的概率分布
例题,
在相同条件下,对目标独立地进行,次射击,如果每次射击的命中率为0.7,求:
(,)击中目标,次的概率;
(,)击中目标不少于,次的概率;
(,)击中目标次数少于,的概率。
函数
例题,函数
CDF.BINOM(quant, n, prob) Numeric. Returns the cumulative
probability that the number of successes in n trials, with probability
prob of success in each, will be less than or equal to quant. When n is
1, this is the same as CDF.BERNOULLI.
例题,
在企业生产管理中,检查产品是否合格是不可缺少的一项工作,从而需要了
解合格品和不合格品的概率分布。
假若有1000件产品,其合格率为90%,现从中随机抽出5件,其中有2件
或3件是不合格品的概率为多少,
函数
例题,函数
CDF.HYPER(quant, total, sample, hits) Numeric. Returns the cumulative probability that the number of objects with a specified characteristic, when sample objects are randomly selected from a universe of size total in which hits have the specified characteristic, will be less than or equal to quant.
例题,
某保险公司根据过去发生交通事故的记录估计出1位投保的学生
在一年内遭遇交通事故的概率是0.03。如果随机选取300位学生投保人,试计
算在过去一年里,有4 位或少于4位学生遭遇交通事故的概率。
函数
例题,函数
CDF.POISSON(quant, mean) Numeric. Returns the cumulative probability that a value from the Poisson distribution, with the specified mean or rate parameter, will be less than or equal to quant.
例题,
某工厂生产的金属棒的长度服从均值为40厘米,标准差为0.45厘米的
正态分布,问:随机选取的一个金属棒的长度介于39.8厘米和40.6厘米之间的
概率是多少,(,)一个金属棒的长度超过某长度的概率是0.82,该长度是多
少,
函数,、,
例题,函数
CDF.NORMAL(quant, mean, stddev) Numeric. Returns the cumulative probability that a value from the normal distribution, with specified mean and standard deviation, will be less than quant.
例题,函数
IDF.NORMAL(prob, mean, stddev) Numeric. Returns the value from the normal distribution, with the specified mean and standard deviation, for which the cumulative probability is prob.
本章小结
随机变量所有可能的取值及其相应的概率,称为概率分布,它可分为离散型
和连续型两类。二项分布是最常见的离散型分布,正态分布是最常见的连续型分
布。
在SPSS中,运用Transform菜单中的Compute过程完成概率分布的计算。
概率P(x=k)一般用pdf表示,分布函数P(x?k)一般用cdf表示。输入的参数均
是各分布的特征值。对连续型,只需计算cdf,对离散型,需要计算pdf和cdf。
范文三:第4章 几种常见的概率分布
第四章 几种常见的概率分布
第一节 二项分布 一、二项总体 1. 定义
由非此即彼事件构成的总体,叫做二项总体(binomial population) 孵n 枚种蛋的出雏数、n 头病畜治疗后的治愈数、n 尾鱼苗的成活数等 2. 表示方法
通常给“此”事件以变量“1”,具概率φ ,给“彼”事件以变量“0”,具概率1- φ 。二项总体又称0、1总体。
● 在n 重贝努利试验中,事件A 可能发生0,1,2,?,n 次,现在我们来求事件A 恰
好发生k(0≤k ≤n) 次的概率Pn(k)。 ● 先取n=4,k=2来讨论。在4次试验中,事件A 发生2次的方式有 C
4
2
● 其中Ak(k=1,2,3,4)表示事件A 在第k 次试验发生;
k (k=1,2,3,4)表示事件A 在
第k 次试验不发生。由于试验是独立的,按概率的乘法法则,于是有
● 由于以上各种方式中,任何二种方式都是互不相容的,按概率的加法法则,在4 次试
验中,事件A 恰好发生2次的概率为
● 一般,在n 重贝努利试验中,事件A 恰好发生k(0≤k ≤n) 次的概率为
k k n -k
P (k)=C k =0, 1, 2, , n n n p q
二、二项分布
如果我们每次独立抽取二项总体的n 个个体,则所得变量X 将可能有0,1,…n ,共n+1种变量有它各自的概率而组成一个分布。这个分布就叫做二项概率分布,或简称二项分布(binomial distribution) 由此得到计算二项分布任何一项概率的通式为:p(x) =Cnx φ x(1- φ)n-x
二项分布是一种离散型随机变量的概率分布
性质
x x n -x C ?(1-?) =1∑n x =0
m
n
x P (x ≤m ) =∑C n ?x (1-?) n -x
x =0
P (x ≥m ) =
x x n -x C ?(1-?) ∑n x =m
n
x
n
P (m 1≤x ≤m 2) =p n (m 1≤k ≤m 2) =
x =m 1
∑C
m 2
p x q n -x
● 例1:若研究施用某种农药后蚜虫的死亡数,设死虫子为0,其概率为0.3;其活的为
1,概率为0.7。如每次观察5只,结果将有0(5只全死)、1(4死1活)、2(3死2活)、3(2死3活)、4(1死4活)、5(5全活),共6种变量。由这6种变量的相应概率组成的分布,就是n=5时活虫数的二项分布。
二项式分布的形状 二项概率分布图
三、服从二项分布的随机变量的特征数
总和数 比率 幻灯片11
1. 二项式分布的参数 ● 平均数
● 以总和数表示时μ=n φ ● 以比率表示时 μ= φ
● 方差
● 以总和数表示时σ2=n φ(1- φ) ● 以比率表示时 σ2= φ(1- φ)/n
2. 证明平均数、方差
3. 实例 总和数
比率
4. 二项总体分布及二项分布参数比较
5. 二项分布偏斜度和峭度
四、二项分布应用实例
● 小鼠毛型受一对等位基因控制,Wv 正常直毛对wv 波浪毛为显性。以杂合基因型Wvwv
的小鼠为父本,与纯合基因型wvwv 的小鼠为母本杂交。杂交后代毛型分布符合二项分布。实验只选每窝8只的,多于或少于8
只的都淘汰,预期每窝小鼠毛型表现。
第二节 泊松分布
● 描述在一指定时间范围内或在指定的面积或体积内某一事件出现的个体数的分布 ● 泊松分布是一种离散型随机变量的概率分布
实例
调查某种猪场闭锁育种群仔猪畸形数,共记录200窝, 畸形仔猪数的分布情况如下表所示。试判断畸形仔猪数是否服从泊松分布。 畸形仔猪数统计分布
解:根据泊松分布的平均数与方差相等这一特征,若畸形仔猪数服从泊松分布,则由观察数据计算的平均数和方差就近于相等。样本均数和方差S2计算结果如下:
可以认为畸形仔猪数服从泊松分布。 幻灯片24
麦田内,平均每10 m2有1株杂草,现在要问每100m2麦田中,有0株杂草,有1株
杂草,有2株杂草,?的概率是多少?
第三节 正态分布
两头少,中间多,两侧对称
一、正态分布的定义
若连续型随机变量x 的概率分布密度函数为
f (x ) =
1
σ2π
e
-
(x -μ) 22σ2
-∞<><∞, σ=""> 0
其中μ为平均数,σ2为方差,则称随机变量x 服从正态分布(normal distribution), 记为x ~N(μ, σ2) 。
随机变量X 的落入任意区间(a ,b )概率:
相应的概率分布函数为
(x -μ) 22σ2
F (x ) =
1
σ2?
x
-∞
e
-
dx
二、正态分布曲线
1.正态分布密度函数的图像
以x=μ为对称轴作对称分布,曲线有个最高点,以此点的横坐标为中心,向两边单调下降。
连续型随机变量的概率分布 2. 正态分布的特征
(1)
正态分布密度曲线是单峰、对称的悬钟形曲线,对称轴为x=μ;
(2) f(x)在x=μ处达到极大,极大值 ; (3) f(x)是非负函数,以x 轴为渐近线,分布从-∞至+∞;
(4) 曲线在x=μ±σ处各有一个拐点,即曲线在(-∞, μ-σ) 和(μ+σ,+∞) 区间上是下凸的,在[μ-σ, μ+σ]区间内是上凸的;
(5) 正态分布有两个参数,即平均数μ和标准差σ。μ是位置参数。 当σ恒定时,μ愈大,则曲线沿x 轴愈向右移动;反之,μ愈小,曲线沿x 轴愈向左移动。σ是变异度参数,如下图所示。当μ恒定时,σ愈大,表示x 的取值愈分散, 曲线愈“胖”;σ愈小,x 的取值愈集中在μ附近,曲线愈“瘦”。
(6) 分布密度曲线与横轴所夹的面积为1,即:
-1
P (-∞
+∞
(x -μ) 22σdx =1
三、标准正态分布
1. 标准正态分布定义
μ=0,σ2=1的正态分布为标准正态分布(standard normal distribution)。标准正态分布的概率密度函数及分布函数分别记作φ (u)和Φ(u)
?(u ) =
φ(u ) =
12u 2-e 2
u
-12u 2
12e ?-∞
du
随机变量u 服从标准正态分布,记作u ~N(0,1)
2. 标准正态分布曲线
标准正态分布密度函数曲线 分布函数曲线
● x=0时,φ(x) 达到最大值 (1) 关于点(0,0.5)对称,该点也 ●
是它的拐点 ● (2)x取值离原点越远,φ (x) (2) 曲线以y = 0和y = 1为渐近线; ● (3)关于y 轴对称,即φ(x)= φ (- x) (3) Ф(1.960)-Ф(-1.960) = 0.95
● (4)在x=1有两个拐点 (4) Ф(2.576)-Ф(-2.576) = 0.99 (5)曲线与x 轴间所夹面积为1 ● 由于正态分布的重要性,它的密度函数及分布函数的数值都已被编成表格备查(附表2) 。 ● 注意的是多数表中只给出x ≥0的φ (x)和Ф(x)值,这是因为由它们的对称性,有:
?(-x ) =?(x ), Φ(-x ) =1-Φ(x )
● 因此可容易地算出x 任意取值时φ (x)和Ф(x)的值。 3. 标准正态分布的概率计算
设u 服从标准正态分布,则u 在[u1,u2]内取值的概率为:
1
P (u 1≤u
2π
?
u 2
u 1
e
1-u 22
1du =
2π
?
u 2
-∞
e
1-u 22
1du -
2π
?
u 1
-∞
e
1-u 22
du
=Φ(u2)-Φ(u1)
常用关系式:
P(0≤u ≤ u1) =Φ(u1)-0.5 P(u≥u1) =Φ(-u1) P(|u |≥u1)=2Φ(-u1)
P(|u |≤ u1)=1-2Φ(-u1) P(u1≤u ≤ u2) =Φ(u2)-Φ(u1) 幻灯片35
例:已知u ~N(0,1) ,试求:
(1) P(uμ+1.960σ)=0.025
● 例如:x 落在(μ-2.576σ, μ+2.576σ) 之外的α为0.01,而α/2为0.005,即
P(xμ+2.576σ)=0.005
例三,求α=0. 05和α=0. 01的上侧临界值、下侧临界值和双侧临界值。
解:
(1) α=0. 05时,上侧临界值u 查表3
0. 05=1. 645;
双侧临界值 u 查表3
0. 05(双侧) =u 0. 025=1. 96
查表(2) α=0. 01时,上侧临界值u 3
0. 01=2. 326;
所以,下侧临界值-u 0. 01=-2. 326;
双侧临界值 u 查表0. 01(双侧) =u 0. 005=3
2. 576
例如,已知u ~N(0,1)试求:
(1) P(u<-u α)+P(u≥ u α)=0.10的 u α
(2) P(-
u α≤u <u α﹚=0.86的u α
解:
(1) P(u<-
u α )= P(u≥ u α )=0.10/2=0.05=α
由附表3查得:
u 0. 05=1.645
(2) P (- u α ≤u < u α )=0.86 ,α=(1- P (- u α ≤u < u α(1-0.86)/2=0.14/2=0.07 由附表3查得:
u 0. 07 =1.476
例如:已知猪血红蛋白含量x 服从正态分布
))/2=
X~ N(12.86,1.332) ,
若P(x<L1) =0.03, P(x≥L2)=0.03,求L1, L2 解:由题意可知
P (x
x -12. 86L -12. 86
<1) =p="" (u=""><-u α)="0.">
1. 331. 33
P (x ≥L 2) =
由附表3查得:
x -12. 86L 2-12. 86P (≥) =P (u ≥u α) =0. 03
1. 331. 33
u 0. 03 =1.881,所以
(L1-12.86)/1.33=-1.881,
(L2-12.86)/1.33=1.881 即 L1 ≈10.36,L2 ≈15.36。 7. 中心极限定理(独立同分布)
● 研究随机变量和的极限分布是正态分布的一类定理,称为中心极限定理。
● 假设被研究的随机变量X ,可以表示为许多相互独立的随机变量Xi 的和。如果Xi 的数
量很大,而且每一个Xi 对于X 所起的作用又很小,则X 可以被认为服从或近似地服从正态分布。 设随机变量序列
X 1, X 2, , X n ,
独立于一分布内, 且有期望和方差:
E (X k ) =μ, D (X k ) =σ2>0, k =1, 2,
则对于任意实数 x,
Y n =
n
∑
k =1
X k -n μ记
则 Y n 为k =1
∑X k
n
的标准化随机变量。
lim P (Y n ≤x )=Φ(x )
n →∞
近似
即 n 足够大时,Y n 的分布函数近似于标准正态随机变量的分布函数
Y n ~N (0, 1)
∑X k =
k =1
n
Y n +n μ
近似服从
N (n μ, n σ2)
?n X -n μ? ∑k ?1k =1 ?lim P ≤x =n →∞ ? ?
??
已知μ、σ,不论总体是否呈正态分布,
n 充分大,其平均数X 服从N(μ, σ2/n)
?-∞e
x
t 2-2
dt
=Φ(x )
U =
1n
X i -μ∑n i =1
例:炮火轰击敌方防御工事 100 次, 每次轰击命中的炮弹数服从同一分布, 其数学期望为 2 , 方差为1.52. 若各次轰击命中的炮弹数是相互独立的, 求100 次轰击: (1) 至少命中180发炮弹的概率;
(2) 命中的炮弹数不到200发的概率。 幻灯片54
n
解 设 X k 表示第 k 次轰击命中的炮弹数
E (X k ) =2, D (X k ) =1. 52, k =1, 2, , 100
X 1, X 2, , X 100
100
相互独立,
设 X 表示100次轰击命中的炮弹数, 则
X =∑X k , E (X ) =200, D (X ) =225,
k =1
由中心极限定理, 有
X
近似
~N (200, 225)
180-200??P (X ≥180) ≈1-Φ ?
15??
(1)
=1-Φ(-1. 3) =Φ(1. 3) =0. 91
200-200??0-200??P (0≤X <200) ≈φ="" ?-φ="">
(2)
=Φ(0) -Φ(-13. 33) =0. 5
范文四:第3章 几种常见的概率分布律
第三章 几种常见的概率分布律
3.1 有4对相互独立的等位基因自由组合,问有3个显性基因和5个隐性基因的组合有多少种?每种的概率是多少?这一类型总的概率是多少?
答:代入二项分布概率函数,这里φ=1/2。
8! ?1??1?56?1?
p (3)==0. 21875 ? ?=56 ?=
3! 5! ?2??2?256?2?
结论:共有56种,每种的概率为0.003 906 25(1/256 ) ,这一类型总的概率为
5
3
8
0.218 75。
3.2 5对相互独立的等位基因间自由组合,表型共有多少种?它们的比如何? 答:(1)
?31?
+??44?
5
5
?3??3??1??3??1??3??1??3??1??1?= ?+5 ? ?+10 ? ?+10 ? ?+5 ? ?+ ?
?4??4??4??4??4??4??4??4??4? ?4?
4322345
表型共有1+5+10+10+5+1 = 32种。
5
(2)
243?3?P (5显)= ?==0. 2373
1024?4?
?3??1?5?81
P (4显1隐)=5 ? ?==0. 3955
?4??4?102410?27?3??1?
P (3显2隐)=10 ? ?==0. 2637
1024?4??4?10?9?3??1?
P (2显3隐)=10 ? ?==0. 08789
1024?4??4?5?3?3??1?
P (1显4隐)=5 ? ?==0. 01465
1024?4??4?
1?1?
P (5隐)= ?==0. 0009766
41024??
5
42
3
3
2
4
它们的比为:243∶81(×5) ∶27(×10) ∶9(×10) ∶3(×5) ∶1 。
3.3 在辐射育种实验中,已知经过处理的单株至少发生一个有利突变的概率是φ,群体中至少出现一株有利突变单株的概率为P a ,问为了至少得到一株有利突变的单株,群体n 应多大?
答: 已知φ为单株至少发生一个有利突变的概率,则1―φ为单株不发生一个有利突变的概率为:
(1-φ)n =1-P a
n lg (1-φ)=lg (1-P a )
lg (1-P a )n =
lg (1-φ)
3.4 根据以往的经验,用一般的方法治疗某疾病,其死亡率为40%,治愈率为60%。今用一种新药治疗染上该病的5名患者,这5人均治愈了,问该项新药是否显著地优于一般疗法?(提示:计算一般疗法5人均治愈的概率,习惯上当P (5人均治愈)> 0.05时,则认为差异不显著;当P (5人均治愈)
<>
答:设P (治愈)=φ= 0.60,则5人均治愈的概率为: P = p = (0.60) = 0.077 76
P >0.05
所以该药物并不优于一般疗法。
3.5 给一组雌雄等量的实验动物服用一种药物,然后对存活的动物分成5只为一组,进行抽样试验。试验结果表明,5只均为雄性的频率为1 / 243,问该药物对雌雄的致死作用是否一致?
答:设p 为处理后雄性动物存活的概率,则
p =
5
55
1
24333
因此,对雄性动物的致死率高于对雌性动物的致死率。
=
1
5
p =
1
3.6 把成年椿象放在?8.5℃下冷冻15分钟,然后在100个各含10只椿象的样本中计算死虫数,得到以下结果:
死虫数 样本数
0 4
1 21
2 28
3 22
4 14
5 8
6 2
7 1
8 0
9 0
10 0
合计 100
计算理论频数,并与实际频数做一比较。
答:先计算死虫数C :
C = 0×4+1×21+2×28+3×22+4×14+5×8+6×2+7×1 = 258 死虫率 φ= 258 / 1 000 = 0.258 活虫率 1 –φ= 0.742
展开二项式(0.742 + 0.258)10 得到以下结果:
0.050 59+0.175 90+0.275 22+0.255 19+0.155 28+0.064 79+0.018 774
-3-4-5-6
+3.730 2×10+4.863 8×10+3.758 2×10+1.307×10
将以上各频率乘以100得到理论频数,并将实际数与理论数列成下表。
死虫数 0 1 2 3 4 5 6 7 8 9 10
3.7 人类染色体一半来自父亲,一半来自母亲。在减数分裂时,46条染色体随机分配到两极,若不考虑染色体内重组,父亲的22条常染色体重新聚集在一极的概率是多少?12条父亲染色体和11条母亲染色体被分配到同一极的概率又是多少?常染色体的组合共有多少种?从上述的计算可以看出变异的广泛性,若再考虑染色体内重组,新组合染色体的数目就更惊人了。
?1? ?
答:(1)P (父亲22条常染色体重新聚集于同一极) = ?2?
22
实际数
4 21 28 22 14 8 2 1 0 0 0 理论数 5.1 17.2 27.5 25.5 15.5 6.5 1.9 0.4 0 0 0 偏差 -1.1 3.8 0.5 -3.5 -1.5 1.5 0.1 0.6 0 0 0
=2. 38?10
-7
(2)P (12条父亲染色体和11条母亲染色体被分配到同一极)
23! ?1??1?1352078
==0. 1612 ? ?
8388608 = 11! 12! ?2??2?
22
(3)共有2 = 4 194 304种。
1112
3.8 生男生女的概率各为1/2,问在一个医院中,连续出生30名男孩及30名性别交错的新生儿的概率各为多少?
?1? ?
答:P (连续出生30名男孩)=?2?
30
=
30
11073741824=
1536870912
=9. 3132?10
-10
=1. 8626?10
-9
?1?2 ?
P (30名性别交错不同者)=?2?
3.9 在显性基因频率很低时,出现显性性状的个体一般为杂合子。一名女子是蓬发者(显性性状),在她的全部六名孩子中,(1)其中第一名孩子,(2)其中第一和第二名孩子,(3)全部六名孩子,(4)任何一名曾孙(或曾孙女)中,发生蓬发的概率是多少?
答: 设:P (子女蓬发)= φ= 1/2 P (子女非蓬发)= 1 – φ= 1/2
则(1)P (其中第一名子女蓬发)=(1/2)(1/2)5 = 0.015 625 (2)P (只有第一和第二名孩子蓬发)= (1/2)2(1/2)4 = 0.015 625 (3)P (全部六名子女)= (1/2) = 0.015 625
(4)P (任何一名曾孙蓬发)= P (任何一名儿子蓬发)P (任何一名孙子蓬发|蓬发的儿子)P (任何一名曾孙蓬发|蓬发的孙子)
=(1/2×1/2) (1/2×1/2) (1/2×1/2) = 0.015 625
3.10 在数量性状遗传中,F 1的性状介于双亲之间,F 2的性状向双亲方向分离。这是一个二项分布问题,根据二项展开式,计算控制某性状的基因个数,假设出现亲本性状的频率为a 。
答:设:P (正效应基因频率)= p
p =a n lg p =lg a n =
lg a lg p
n
6
则
3.11 计算μ = 0.1,0.2,1,2,5时,泊松分布的γ1和γ2,绘制概率分布图并做比较。
p (y )=
μ
y
答:泊松分布的概率函数:
y ! E
μ
(1)μ =0.1时
y 0 1 2 3 4
将μ = 0.1,0.2,1,2,5分别代入上式。
p (y )
0.904 8 0.090 48 0.004 524 0.000 150 8 0.000 003 77
γ1=γ2=
1
μ
1
=10. 1
10. 1
=3. 1623
μ
==10
(2)μ =0.2时
y 0 1 2 3 4
γ1=γ2=
1
p (y )
0.818 7 0.163 7 0.016 39 0.001 092 0.000 054 58
10. 2
=2. 2361
μ
1
=10. 2
μ
==5
(3)μ = 1时
y 0 1 2 3 4 5 6 7
γ1=γ=1
p (y )
0.367 9 0.367 9 0.183 9 0.061 31 0.015 33 0.003 066 0.000 510 9 0.000 072 99
μ1
=11
1=1
=
11
=1
(4)μ = 2时
2
μ
=
p (y ) y 0.135 3 6 0.270 7 7 0.270 7 8 0.180 4 9 0.090 22 10 0.036 09
γ1=γ2=
1μ1μ=12=
12=0. 5
=
11. 4142
y 0 1 2 3 4 5
p (y ) 0.012 03 0.003 437 0.000 859 3 0.000 190 9 0.000 038 19 y 9 10 11 12 13 14 15 16
p (y ) 0.036 27 0.018 13 0.008 424 0.003 434 0.001 321 0.000 471 7 0.000 157 2 0.000 049 14
=0. 7071
(5)μ = 5时 y p (y ) 0 0.006 738 1 0.033 69 2 0.084 22 3 0.140 4 4 0.175 5 5 0.175 5 6 0.146 2 7 0.104 4 8 0.065 28
γ1=γ2=
1
=1515=
12. 2361
=0. 4427
μ1
μ
==0. 2
可见,随着μ的增大泊松分布越来越接近于“正态”
的。
3.12 随机变量Y 服从正态分布N (5,42) ,求P (Y ≤0) ,P (Y ≤10) ,P (0≤Y ≤15) ,P (Y ≥5) ,P (Y ≥15) 的值。
答:
?10-5?
P (Y ≤10)=φ ?=φ(1. 25)=0. 89435
?4??0-5?
P (Y ≤0)=φ ?=φ(-1. 25)=0. 10565
?4?
?15-5??0-5?
P (0≤Y ≤15)=φ ?-φ ?=φ(2. 5)-φ(-1. 25)=0. 99379-0. 10565=0. 88814
44?????5-5?
P (Y ≥5)=1-φ ?=1-φ(0)=1-0. 5=0. 5
?4??15-5?
P (Y ≥15)=φ -?=φ(-2. 5)=0. 00621
4??
或者使用SAS 程序计算,结果见下表:
OBS MU SIGMA Y1 LOWERP Y2 UPPERP MIDP 1 5 4 10 0.89435 . . .
2 5 4 0 0.10565 . . .
3 5 4 0 0.10565 15 0.00621 0.88814 4 5 4 . . 5 0.50000 . 5 5 4 . . 15 0.00621 .
3.13 已知随机变量Y 服从正态分布N (0,52) ,求y 0 分别使得P (Y ≤y 0)=0.025, P (Y ≤y 0)=0.01, P (Y ≤y 0)=0.95及 P (Y ≥y 0)=0.90。
答:
P (Y ≤y 0)=0. 025P (Y ≤y 0)=0. 01P (Y ≤y 0)=0. 95P (Y ≥y 0)=0. 90
?y 0-0?
?=0. 0255???y 0-0?
?=0. 015??
y 0-05y 0-05y 0-055
φ =-1. 96
y 0=-9. 8
φ φ
=-2. 326y 0=-11. 63=1. 645=-1. 283
y 0=8. 225y 0=-6. 415
?y 0-0?
?=0. 955??
?y -0?1-φ 0?=0. 90
5??
y 0-0
3.14 细菌突变率是指单位时间(细菌分裂次数)内,突变事件出现的频率。然而根据以上定义直接计算突变率是很困难的。例如,向一试管中接种一定量的细菌,振荡培养后铺平板。在平板上发现8个突变菌落。这8个突变细菌究竟是8个独立的突变事件呢,还是一个突变细胞的8
个子细胞是很难确
定的。但是有一点是可以肯定的,即,没有发现突变细胞的平皿一定没有突变事件出现。
向20支试管中分别接种2×10个大肠杆菌,振荡培养后铺平板,同时接种T 1噬菌体。结果在9个平皿中出现数量不等的抗T 1噬菌体菌落。11个平皿上没有出现。已知平皿上突变菌落数服从泊松分布并且细胞分裂次数近似等于铺平板时的细胞数。利用泊松分布概率函数计算抗T 1突变率。
答:已知接种细胞数为n ,n 即可认为是细胞分裂次数。若每一次细胞分裂的突变率为u ,那么每一试管中平均有un 次突变事件发生(μ)。从泊松分布概率函数可知,无突变发生的概率f (0)=E -un 。实验结果无突变的平皿数为11个,即f (0)=11/20=0.55。解下式
-un
E =0. 55
7
即可求出突变率u 。已知n =0.2×108,代入上式得到u =3×10-8。
3.15 一种新的血栓溶解药t -pA ,据说它能消除心脏病发作。在一次检测中的7名检测对象,年龄都在50岁以上,并有心脏病发作史。他们以这种新药治疗后,6人的血栓得到溶解,1人血栓没有溶解。
假设t -pA 溶解血栓是无效的,并假设,不用药物在短时间内心脏患者血栓自己溶解的概率φ是很小的,如φ=0.1。设y 为7名心脏患者中血栓在短时间内可以自动溶解的患者数。问:(1)若药物是无效的,7名心脏患者中的6名血栓自动溶解的概率是多少? (2)Y ≥6是否为一稀有事件,你认为药物是否有效? 答:(1) ф= 0.1 1-ф=0.9 n=7 y =6,
p (6)=C 7(0. 1)(0. 9)=
6
6
1
7
7
7
7! 6! 1!
(0. 1)6(0. 9)1
=0. 0000063
(2) p (7)=C (0. 1)=0. 0000001
-6
P (Y ≥6) = 0.000 006 3+0.000 000 1 = 6.4×10。
结论:在不用药的情况下,7名病人中6名患者的血栓自动溶解的事件是一个小概率事件,因此药物有效。
3.16 一农药商声称,用他的农药喷洒玉米后,90%的玉米植株中不再有活的玉米螟。为了验证这种说法,喷药后随机抽出25株玉米,发现7株中仍有活的玉米螟。
(1)若农药商的说法是正确的,在25株玉米中包含7株和7株以上有活玉米螟的概率是多少? (2)在25株玉米中有7株有活玉米螟,你是否认为农药有效率达不到90%? 答:(1)
P (Y ≥7)=1-P (Y ≤6)
025242233220123
?C 25(0. 1)(0. 9)+C 25(0. 1)(0. 9)+C 25(0. 1)(0. 9)+C 25(0. 1)(0. 9)=1-
+C 4(0. 1)4(0. 9)21+C 5(0. 1)5(0. 9)20+C 6(0. 1)6(0. 9)19
252525?
?
???
=0. 009
(2) 是
3.17 设计一实验用来检验号称心灵感应者是否有特异功能(ESP)。将5张卡片洗匀随机抽出一张,不准心灵感应者看,让他判断是哪一张。实验共重复20次,记录正确判断次数(假设20次重复间是随机的)。假设心灵感应者是猜的,没有ESP ,那么
(1)每次得到正确结果的概率是什么? (2)在20次重复中,期望正确判断数是多少? (3)正确判断6次和6次上的概率是多少?
(4)假设心灵感应者在20次重复中判断正确6次,是否可以证明心灵感应者不是猜的,而是真正的ESP ?
答:(1)p = 1/5。
(2)E (Y ) = np = 20×1/5 = 4。
?1??4?
P (Y ≥6)=C ? ?
?5??5?(3)
620
6
14
+???+C
(4)不能。因为在猜想的情况下,20次重复中判断正确6次的概率为0.196,将近20%,已不是小概率事件,非心灵感应者有可能得到这样的结果。
3.18 据一个生化制药厂报告,在流水线上每8小时的一个班中,破碎的安瓿瓶数服从泊松分布,μ=1.5。问:
(1)夜班破碎2个瓶子的概率是多少 ? (2)在夜班打碎2个以下的概率是多少? (3)在早班破碎2个以上的概率是多少?
(4)在一天连续三班都没有破碎的概率(假设三班间是独立的)?
p (2)=
1. 52! E
21. 5
2020
?1??4? ? ??5??5?
020
=0. 196
答:(1)
=0. 251
11. 5
(2)
p (0)+p (1)=
1. 50! E
1. 5
+
1. 51! E
=0. 223+0. 335=0. 558
(3)P (x >2)=1-p (2)-p (1)-p (0)=0. 191 (4)记A 为每个班没有破碎的事件,则
3
P (AAA )=[p (0)]=0. 223=0. 011
3
范文五:常见的概率分布
1.017/1.010 第10课
常见的概率分布
常见的连续分布的概率密度函数和累积分布度函数
每个分布函数都取决于几个分布参数。
1、均匀分布(分布参数a,b):
2、指数分布(分布参数a):
3、单变量正态分布(高斯分布)
(分布参数
):
无封闭的形式,以表列出
4、对数正态分布(分布参数
):
无封闭形式,以表列出
练习:求取数据的最优分布
访问英国地理调查网站,站点在:
选择“Village survey(59k)”,下载孟加拉国供水井的砷数据。
当你选择“Village survey (59k)”这个连接时,一张EXCEL表格将出现在你的浏览器中。我们关心的是第O栏中砷数据的“As arsenator”值(“arsenator” 指特定领域测定总砷的方法)。不是让你用MATLAB命令来下载数据,而仅仅是选择O栏的数值、复制、然后粘贴到MATLAB程序中。你可以用下述表达式将数据粘贴到程序中:
arsenic_data = [
当数据出现在你的程序中之后,再输入 ] 结束。结果应该是一个名为 arsenic_data 的长列向量,它包含了从电子表格中获得的数值。你可以直接在将这一表达式插入到你的程序中(还有其它的方法来导入数据的-如果你愿意,可以自由地用其它方法)。
在你程序的余下部分画出样本的CDF图和砷数据的直方图。
构造一个MATLAB函数cdffit(data, ndist, p1, p2),使样本砷的CDF函数与上面介绍的几个常用的CDF函数中的一个相拟合, 以 ndist=1, 2, 3, or 4 作为索引,输入量p1和p2是分布参数。调节这些参数以获得最佳拟合。
把样本和假定的分布函数画在同一坐标轴上(用MATLAB的 hold 函数)。
提供你选出的比较满意的假定分布函数图的复本,并简单地说明你为什么要选它。对AA栏中铁的数据重复整个过程。确保删除任何非数字量(如“<”)。并且,用你选择的最优分布函数计算砷水平超过最新美国标准(最高上限)10μg/L的概率。
相关的MATLAB函数:cdfplot,hold,unifcdf,expcdf,normcdf,logcdf
MATLAB函数文件:cdffit.m
版权属于麻省理工学院 2003年
最后修改日期 2003年10月8日



 你说无所谓的有所谓
你说无所谓的有所谓

