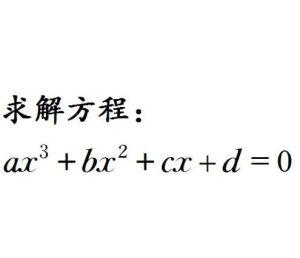
范文一：一元三次方程的根的探究

关于一元三次方程的根的探究

1. 因式分解法

因式分解法不是对所有的三次方程都适用，只对一些三次方程适用．对于大多数的三次方程，只有先求出它的根，才能作因式分解．当然，因式分解的解法很简便，直接把三次方程降次．例如：解方程x^3-x=0

对左边作因式分解，得x(x+1)(x-1)=0,得方程的三个根：x1=0,x2=1,x3=-1.

2. 另一种换元法

对于一般形式的三次方程，先用上文中提到的配方和换元，将方程化为x+px+q=0的特殊型．令x=z-p/3z,代入并化简，得：z-p/27z+q=0.再令z=w,代入，得：w+p/27w+q=0．这实际上是关于w 的二次方程．解出w, 再顺次解出z,x.

3. 盛金公式解题法

三次方程应用广泛。用根号解一元三次方程，虽然有著名的卡尔丹公式，并有相应的判别法，但使用卡尔丹公式解题比较复杂，缺乏直观性。范盛金推导出一套直接用a 、b 、c 、d 表达的较简明形式的一元三次方程的一般式新求根公式，并建立了新判别法．

盛金公式

一元三次方程aX^3＋bX^2＋c X ＋d=0，（a ，b ，c ，d ∈R ，且a≠0）。 重根判别式：A=b^2－3ac ；B=bc－9ad ；C=c^2－3bd ， 总判别式：Δ=B^2－4AC 。 当A=B=0时，盛金公式①： X1=X2=X3=－b/(3a)=－c/b=－3d/c。 当Δ=B^2－4AC>0时，盛金公式②： X1=(－b －(Y1)^(1/3)－(Y2)^(1/3))/(3a)；

X2，3=(－2b ＋(Y1)^(1/3)＋(Y2)^(1/3))/(6a)±i3^(1/2)((Y1)^(1/3)－(Y2)^(1/3))/(6a)， 其中Y1，2=Ab＋3a(－B±(B^2－4AC)^(1/2))/2，i^2=－1。 当Δ=B^2－4AC=0时，盛金公式③： X1=－b/a＋K ； X2=X3=－K/2， 其中K=B/A，(A≠0)。

当Δ=B^2－4AC<0时，盛金公式④： x1="(－b">

X2，3=(－b ＋A^(1/2)(cos(θ/3)±3^(1/2)sin(θ/3)))/(3a)，

其中θ=arccosT，T=(2Ab－3aB)/(2A^(3/2))，(A>0，－1<><>

盛金判别法

①：当A=B=0时，方程有一个三重实根；

②：当Δ=B^2－4AC>0时，方程有一个实根和一对共轭虚根； ③：当Δ=B^2－4AC=0时，方程有三个实根，其中有一个两重根； ④：当Δ=B^2－4AC<>

盛金定理

当b=0，c=0时，盛金公式①无意义；当A=0时，盛金公式③无意义；当A≤0时，盛金公式④无意义；当T 1时，盛金公式④无意义。

当b=0，c =0时，盛金公式①是否成立？盛金公式③与盛金公式④是否存在A≤0的值？盛金公式④是否存在T 1的值？盛金定理给出如下回答： 盛金定理1：当A=B=0时，若b=0，则必定有c=d=0（此时，方程有一个三重实根0，盛金公式①仍成立）。

盛金定理2：当A=B=0时，若b≠0，则必定有c≠0（此时, 适用盛金公式①解题）。 盛金定理3：当A=B=0时，则必定有C=0（此时, 适用盛金公式①解题）。 盛金定理4：当A=0时，若B≠0，则必定有Δ＞0（此时，适用盛金公式②解题）。 盛金定理5：当A 0（此时，适用盛金公式②解题）。 盛金定理6：当Δ=0时，若B=0，则必定有A=0（此时，适用盛金公式①解题）。 盛金定理7：当Δ=0时，若B≠0，盛金公式③一定不存在A≤0的值（此时，适用盛金公式③解题）。

盛金定理8：当Δ0时，不一定有A ０时，

（ｘ）＝３ｘ２＋ｐ≥０（等号至多在个别点成立），ｇ′

所以ｇ（ｘ）在（－∞，＋∞）内严格递增且连续，又

ｇ（－∞）＝－∞，ｇ（＋∞）＝＋∞，故ｇ（ｘ）只有一个零点，即方程（２）有一个实根．

＝２ｂ－９ｂｃ＋２７ｄ＋３ｃ－ｂ（ｘ＋ｂ）＋（ｘ＋ｂ）３

令ｘ′＝ｘ＋ｂ，ｐ＝３ｃ－ｂ，ｑ＝２ｂ－９ｂｃ＋２７ｄ，收稿日期：２００５－０３－２１

作者简介：李密（１９６５－），女，辽宁阜新人，讲师，

主要从事数学及计算机的教学研究。

２

３

３２

图１

图（１）中的三条曲线分别为ｇ（ｘ）当ｑ＞０、ｑ＝０、

６６

金华职业技术学院学报２００６年

ｑ０时，方程（２）有一个负实根；

）＝－２ｐ＋ｑ）! 上下平移曲线ｇ（ｘ），可知方程（２）的实根分布情况

ｍ＝ｇ（

!

②当ｑ＝０时，方程（２）有一个零根；③当ｑ０时，

若ｍ＞０，方程（２）仅有一个负实根；

若ｍ＝０，方程（２）有一个负实根和一个正实

根（二重）；

若ｍ０，方程（２）有两个负实根和一个正实根；

图２

若Ｍ＝０，方程（２）有一个负实根（二重）和一个正实根；

若Ｍ０

方程ｘ３＋ｐｘ＋ｑ＝０一个负实根一个零根一个正实根一个负实根

一个负实根和一个正（二重）实根一个负实根和两个正实根一个负根、一个零根、一个正根两个负实根和一个正实根一个负（二重）实根和一个正实根一个正实根

ｐ＞０ｑ＝０ｑ０ｑ＞０ｍ＝０ｍ０Ｍ＝０Ｍ＜０

参考文献：

［１］刘玉琏，傅沛仁．数学分析讲义［Ｍ］．北京：高等教育出版社，１９８５．［２］华东师范大学数学系．数学分析（上册）［Ｍ］．北京：人民教育出版社，１９８０．［３］同济大学应用数学系．高等数学［Ｍ］．北京：高等教育出版社

，１９７８．

转载请注明出处范文大全网 » 一元三次方程的根的探究