范文一：拉伸常用计算公式

常用计算公式:

1、钢板拉伸:

原始截面积=长×宽

原始标距=原始截面积的根号×5.65 LS0=K0

k为5.65 S为原始截面积 0

断后标距-原始标距

断后伸长率= ×100%

原始标距

原始截面积—断后截面积 断面收缩率= ×100%

原始截面积

Z=[(AA)/A]100% 0—10

2、圆材拉伸:

2

原始截面积= 4

(=3.1416 D=直径)标距算法同钢板

3、光圆钢筋和带肋钢筋的截面积以公称直径为准， 标距=5×钢筋的直径。断后伸长同钢板算法。

4、 屈服力=屈服强度×原始截面积

最大拉力=抗拉强度×原始截面积

抗拉强度=最大拉力?原始截面积

屈服强度=屈服力?原始截面积

1

5、钢管整体拉伸:

原始截面积=(钢管外径—壁厚)×壁厚×(=3.1416)

标距与断后伸长率算法同钢板一样。

6、抗滑移系数公式:

N=截荷 KN V

P=预拉力平均值之和 1

nf=2

预拉力(KN) 预拉力之和 滑移荷载Nv(KN)

第一组 171.4 342.8 425

第二组 172.5 345 428

第三组 171.5 343 424

2

7、螺栓扭矩系数计算公式:K=

P?d

T=施工扭矩值(机上实测)

P=预拉力

d=螺栓直径

已测得K值(扭矩系数)但不知T值是多少,可用下列

公式算出:T=k*p*d T为在机上做出实际施拧扭矩。K

为扭矩系数，P为螺栓平均预拉力。D为螺栓的公称直

径。

n

2()KK,8、螺栓标准偏差公式: ,i

i,1 ,,

n,1

2K=扭矩系数 K=扭矩系数平均值 用每一组的扭矩系i

数减去平均扭矩系数值再开平方，八组相加之和，再除于7。再开根号就是标准偏差。

例:随机从施工现场抽取8 套进行扭矩系数复验，经检测: 螺栓直径为22

螺栓预拉力分别为:186kN，179kN，192kN，179kN，200kN，205kN，195kN，188kN;

相应的扭矩分别为:

530N?m，520N?m，560N?m，550N?m，589N?m，620N?m， 626N?m，559N?m

K=T/(P*D) T—旋拧扭矩 P—螺栓预拉力 D—螺栓直径(第一步先算K值，如186*22=4092

再用530/4092=0.129，共算出8组的K值，再算出这8组的平均K值，第二步用每组的K值减去平均K值，得出的数求出它的平方，第三步把8组平方数相加之和，除于7再开根号。得出标准差。

解:根据规范得扭矩系数:

3

扭矩系数平均值:

0.110,0.136,0.150 判定扭矩系数为合格 标准偏差:

n

2()KK,,i i,1,,

n,1

4

8组相加=0.000183?7=0.000026142857

判定标准偏差为合格 扭剪型螺栓连接副预拉力、紧固轴力P和标准偏差计算公试:

一组扭剪型螺栓M20×70预拉力分别为186.1、184.6、155.3、161.7、152.5、160.7、153.9、162.7

解:紧固轴力平均值为:

8组预拉力相加?8=164.7

标准偏差:

5

8组相加=1236.81?7=176.687142857143

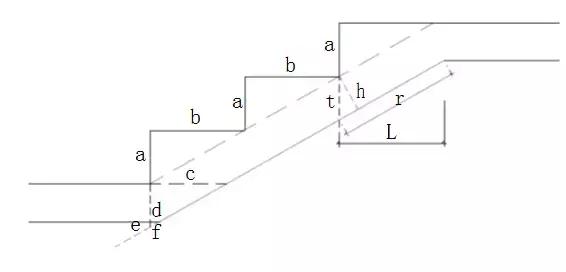
现有一多层钢结构建筑，用设计标高控制安装结束后，发现整体建筑物发生倾斜，对该建筑物用经纬仪检测倾斜量如图所示，α =65?

已知H1=1.5m, ,L=62m, AB之间的距离a=30cm, 11

问:(1)计算整幢建筑物的倾斜量,

(2)整幢建筑物的倾斜是否满足规范要求,

6

A B1 a A1 a A1 B1 B

H 2

A1 B1

H1

H1 α L

i=a/H= 1

9、采用K=2的探头，对外径为500mm的钢管作接触法周向探伤，能扫查到的最大壁厚为多少,

Tm=D/2[1—(K/?1+K?)]=

500/2[1—(2/?1+2?)]=26.5mm

10、超声波的当量Δ=20lgH/H0 (dB) 例:显示屏上显示一波高为80mm,另一波高为20mm，问前者比后者高多少dB,

解:Δ=20lgH/H0 =20lg80/20=20lg4=2×20lg2=12(dB) 注:20lg2=6 20lg4=12 20lg8=18

超声波的当量Δ=20lgH/H0 (dB) 例:显示屏上显示一波高为80mm,另一波高为20mm，问前者比后者高多少dB? 解:Δ=20lgH/H0 =20lg80/20

7

=20lg4

(=2×20lg2)=12(dB)

注:20lg2=6 20lg4=12 20lg8=18(先按lg再按8再×20

计算器不同，有的是先按8再按log再×20)

二次波:二倍板厚,显示深度,实际深度

一次波:水平,显示深度×K值

某一工字钢梁(作为楼盖主梁使用，如图 1 所示)进行使用性能试验(试验荷载控制在弹性范围以内)，为测钢梁在荷载作用下的挠度， 在支座 A、B 以及跨中分别布置了三只百分表，分别为表 1、表 2 和表3，三只百分表在正式试验加载前读数如图 2所示，加载结束时的

-4读数如图 3 所示，实测跨中工字钢下翼缘平均拉应变为 0.41×10 (q)， 试问:(1)根据图中百分表读数推测，该梁刚度是否满足规范要求, (2)根据实测应变值推算荷载 P为多少,(钢材的弹性模量为E=2.06

523×10 N/mm ，工字钢的的截面模量 W=877.6cm ，忽略钢梁自重)(5分)

根据最大挠度控制1/400，荷载条件25kn/m,看能满足的上部荷载要求?

P P Φ? Φ?

A B Φ?

2400 2400 2400

3600 3600

图一: ?0.18 ?0.02 ?5.65

图二: ?0.29 ?0.00 ?5.29

解:? f1=5.65-5.29=0.36 f2=0.29-0.18=0.11 f3=0.02-0.00=0.02

8

f= f1-[( f2+ f3)?2]=0.36-[(0.11=0.02)?2]=0.295

?

(0.41×0.0001×2.06×10000×877.6×1000)

则荷载P为4.1KN/m

11、防火涂料涂粘结(抗拉)强度计算:

?=F/A ?—粘结强度 Mpa F—最大拉伸载荷， A—bb

粘结面积 mm?

22 面积为40mm×40mm

12、防火涂料涂抗压强度计算:

R=P/ A R--抗压强度 P--最大压力载荷量 A—受压

22 面积 mm? 面积为40mm×40mm

某钢结构室外工程施工中，采用了某工程生产的薄型防火涂料，经抽样送到××检测公司进行抗拉强度测试，测试原始记录数据如下:F180N,F270N,F3100N,F475N,F581N。试计算出该防火涂料的抗拉强度值，并判定是否合格。(WH 型防火涂料 fb ?0.04MPa)

解:根据公式:

9

则:

去掉最大和最小值，取三个平均值:

0.050.04 判定为合格

圆的周长公式,,,π r (2×3.14×圆的半径) 或3.14×圆的直径(3.14×Φ,)

圆的面积公式,,π r?

13、超声波焊缝探伤中，用K2的探头探测T=30mm的对接焊缝，仪器按深度1:1调节扫描速度，探伤中在示波屏水平刻度20和40处出现两个缺陷波，求此两个缺陷在焊缝中的位置,

答案:由已知可知，Tn=20,T=30,F1是一次波发现的，F1的水平距f1

离和深度分别为:d=20mm 水平l=kd=2×20=40mm f1f1 f1

又由已知可知，T=30,T=40,2T=60，F2是二次波发现的，F2是水平f2

10

=2T-nT=2×30-1*40=20 mm 距离和深度分别为:df2f2

水平:l= knT=2×1*40=80 mm f2f2

(水平刻度为20的，深度是20mm,水平距离是40 mm)

(水平刻度为40的，深度是20mm,水平距离是80 mm)

14、

延伸率是相对引申计原始标距而言，如引申计原始标距为200mm，拉伸时该部分长度为220mm，则延伸率为10%。

伸长率是对钢材原始标距而言，国际上通常取5倍的钢筋直径为原始标距，如直径为18mm的钢筋，原始标距取90mm，拉伸后该部分长度为120mm，则伸长率为33%。 延伸率

延伸率( δ ):材料在拉伸断裂后，总伸长与原始标距长度的百分比。延伸率按照测量方式的不同分为定倍数A5、A10和定标距A50、A80、A100等。A5是比例试样原始标距与直径的比为5, A10是比例试样原始标距与直径的比为10;A50是非比例试样，原始标距为50mm，A80、A100与之同理。工程上常将δ?5%的材料称为塑性材料，如常温静载的低碳钢、铝、铜等;而把δ?5%的材料称为脆性材料，如常温静载下的铸铁、玻璃、陶瓷等。

断后伸长率

应该称作断裂后伸长率(σh)

最终标距长度(L0):在试件变形前的标距长度。

最终标距长度(Lh):在试件断裂后并且将断裂部分仔细地对合在一起使之处于一直线上的标距长度。

断裂后伸长率的计算公式为:σh=(Lh-L0)/L0*100%

11

范文二：弹性模量计算公式

文档可能在WAP 端浏览体验不佳。建议您优先选择TXT ，或下载源文件到本机查看。 第三章 压弯构件的失稳 轴力偏心作用的构件或同时受轴力和横向荷载作用的构件称为压弯构件. 由于压弯构件兼有 受压和受弯的功能, 又普遍出现在框架结构中, 因此又称为梁柱. 钢结构中的压弯构件多数是截面至少有一个对称轴, 且偏心弯矩作用在对称平面的单向偏心 情况. 对单向偏心的压弯构件, 有可能在弯矩平面内失稳, 即发生弯曲失稳; 也有可能在弯矩作 用平面外失稳, 即弯扭失稳. 其弯曲失稳为第二类稳定问题, 即极值点失稳; 其弯扭失稳对理想 的无缺陷的压弯构件属于第一类稳定问题, 即分支点失稳, 但对实际构件则是极值点失稳. 对理想的两端简支的双轴对称工形截面压弯构件, 在两端作用有轴线压力 P 和使构件产生 同向曲率变形的弯矩 M, 如果在其侧向有足够的支撑 (如图 3.1(b)),构件将发生平面内的弯 曲失稳, 其荷载― 挠度曲线如图 3.2(a)中曲线 a, 失稳的极限荷载为 Pu, 属于极值点失稳. 图 3.1 两端简支理想压弯构件 图 3.2 压弯构件荷载变形曲线 如果在侧向没有设置支撑(如图 3.1(c),则构件在荷载 P 未达到平面内极限荷载 Pu 时, ) 可能发生弯扭失稳, 即在弯矩作用平面内产生挠度 v, 在平面外剪心产生位移u, 并绕纵轴产生 扭转角 (如图 3.1(d),其荷载-变形曲线如图 3.2(b)中曲线 b, 属于分支点失稳, 失稳 ) 的分荷载为 Pyw, ,且 Pyw 3. 1 压弯构件平面内失稳 对压弯构件, 当弯矩作用平面外有足够多支撑可以避免发生弯扭失稳时, 若失稳则只可能发 生平面内弯曲失稳. 当用弹性理论分析理想压弯构件的荷载挠度关系, 可以得到图 3. 3 中的二阶弹性曲线 b, 它 以轴心受压弯构件的分岔点荷载 PE 处引出的水平线 a 为渐近线. 实际压弯构件存在初始缺陷(残余应力、几何缺陷), 材料为弹塑性体. 如按弹塑性理论分析, 荷载挠度曲线将是图中曲线 OABC. 曲线上 A 点标志着杆件中点截面边缘开始屈服, 对应的荷 载为 Pe, 随后塑性向截面内部发展, 构件变形快速增加, 形成 OAB 上升段, 构件处于稳定平衡 状态;B 点为曲线的极值点, 对应的荷载 Pu 为构件在弯矩作用平面内失稳的极限荷载; 到达 B 点以后, 由于弹性区缩小到导致构件抵抗力矩的增加小于外力矩的增加程度, 出现下降段 BC, 52 构件处于不稳定平衡状态. 由失稳全过程可以看出实际压弯构件在弯矩作用平面内的弯曲失稳属 于二阶弹塑性分析的极值点失稳, 不能用弹性理论和平衡微分方程求解极限荷载 Pu, 而可用数 值积分法通过得出荷载挠度曲线后求得极限荷载. 压弯构件平面内弯曲失稳的

弹性分析虽然不能求出极限荷载, 但它是弹塑性分析的基础, 因 此有必要先研究压弯构件平面内弹性失稳. 图 3 .3 压弯构件荷载挠度曲线 3.1.1 压弯构件平面内弹性弯曲性能 在第二章讨论初始几何缺陷对轴心受压构件稳定性能的影响时, 对图 2.13 所示有偏心的轴 心受压杆已作过分析, 即当作偏心压弯构件得出了荷载 P 与构件中点挠度δ 之间的关系曲线. 从式(2.48)中可以看出, 若假设材料是无限弹性体, 则当δ →∞时,P→PE,即临界荷载 P 以欧 拉荷载 PE 为极值. 然而实际材料都是有限弹性的, 由于压弯构件平面内弯曲失稳时, 构件为弹 塑性工作状态, 因此弹性分析只有理论意义. 下面仅讨论两端铰接受轴向压力和平面内横向荷载共同作用的弹性压弯构件的内力与变形 性能. 1. 横向均布荷载作用的压弯构件 横向均布荷载作用的压弯构件 图 3.4(a)所示 为在均布荷载 q 作用下两端铰接的压弯构件. 假定材料完全弹性, 取图 3. 4(c) 所示隔离体, 在距左端 x 处截面的内力矩 M f = EIy ′′ ,外力矩 M e = Py + qx (l x ) 2 ,平衡方程 为 令 k = P EI ,则 2 EIy ′′ + Py = qx(l x ) 2 qx( x l ) 2 EI 2 方程 (3. 1)的特解可写作 y = c1 x + c 2 x + c 3 ,代入方程( 3. 1 ) ,有 y ′′ + k 2 y = (3.1) (Pc1 q 2)x 2 + (Pc 2 + ql 2)x + Pc3 + 2 EIc1 = 0 上式是恒等式, 故 53 c1=q∕(2P) ,c2= -q l ∕(2P) 2 ,c3= -EIq∕P 2 方程( 3. 1 )对应的齐次线性方程 y 〃+k y =0 的通解可写作 y =Asin kχ +Bcos kχ , 则方程 ( 3. 1 ) 的通解为 2 2 y= Asin kχ +Bcos kχ + qχ ∕(2P)-q l χ ∕(2P)-EIq/ P (3.2) 由边界条件 y(0) =0 , y( l )=0 得 A= EIq∕P tg (κ l ∕2) , 2 B=EIq∕P 2 则 q kl qx tg sin kx + cos kx 1 2 (l x ) k EI 2 2k EI 构件在 x = l 2 处有最大挠度 y max , 令 u = kl 2 ,可得 y= 4 (3.3) y max = ql 4 1 cos u ql 4 16 EIu 4 cos u 32 EIu 2 12(2 sec u u 2 2) = y0 5u 4 (3.4) 式中: y 0 = 5ql 4 (384 EI ) 是均布荷载作用下简支梁的最大挠度, 即当 P=0 时, 由式 ( 3. 4 ) 求得 的最大挠度. 式( 3. 4 ) 中括号内的值为考虑轴线压力后最大挠度的放大系数. 图 3.4 均布荷载作用的压弯构件 将 sec u 展开成幂级数, 有 sec u = 1 + 式中 1 2 5 4 61 6 277 8 u + u + u + u + 2 24 720 8064 u= kl l = 2 2 P π = EI 2 P PE 则式( 3. 4 )可写成 y max = y 0 1 + 1.034(P PE ) + 1.0038(P PE ) + ≈ y 0 2 [ ] 1 1 P PE (3.5) 式中 Am = 1 / (1 P / PE ) 是最大挠度的放大系数. 构件中点的最大弯矩为 = Am y0 54 1.028 P PE M max = ql 2 8 + Py max = M 0 1+ 1 P PE β mM = 1 P P = Am M 0 E (3.6) 式中 M 0 = ql 2 8 是均布荷载作用下简支梁跨中的最大弯矩; β m 为等效弯矩系数; Am 为弯矩放大 系数,

用以考虑轴压力 P 产生的二阶效应. 2. 横向集中荷载作用的压弯构件 由图

3.5(c)知, 当 0< x="" ≤="" l="" 2="" 时,="" 平衡方程为="" eiy="" ′′="" +="" py="Qx" 2="" 令="" k="" 2="P" (="" ei="" )="" ,="" 则="" 通解为="" y="" ′′="" +="" k="" 2="" y="Qx" (2="" ei="" )="" (3.7)="" 3="" ql="" (tgu="" u="" )="Ql" 33="" (tgu="" u="" )="y0" 3(tgu3="" u="" )="" (3.9)="" 4="" pu="" 48ei="" u="" u="" 式中="" y="" 0="Ql" 3="" (48="" ei="" )="" 是集中荷载="" q="" 作用在跨中时简支梁的最大挠度,3(tgu="" u="" )="" u="" 3="" 是有轴压力作="" 用时最大挠度放大系数.="" 将="" tgu="" 展成幂级数="" y="A" sin="" kx="" +="" b="" cos="" kx="" qx="" (2="" p="" )="" q="" 引入边界条件="" y="" (0="" )="0" ,="" y="" ′(l="" 2)="0," 得="" b="">

A = sec (kl 2), 则通解 2 Pk Q kl y= sec sec kx kx 2 Pk 2 令 u = kl 2, 当 x = l 2 时, 跨中最大挠度为 ymax = (3.8) tgu = u + u 3 3 + 2u 5 15 +17u 7 315 + 将 u = kl 2 = π 2 P PE 代入, 则式( 3. 9 )可改写为 y max = y 0 1 + 0.987(P PE ) + 0.986(P PE ) + ≈ y 0 2 [ 图 3.5 跨中集中荷载作用的压弯构件 ] 式中 1 (1 P / PE ) 为最大挠度放大系数. 跨中最大弯矩为 1 1 P PE (3.10) M max = Ql 4 + Py max = Ql Pl 2 1 + 4 12 EI (1 P PE ) 55 1 0.178 P PE β m M 0 = =M0 (3.11) 1 P P 1 P P = Am M 0 E E 式中 M 0 = Ql 4 是集中荷载作用下简支梁最大弯矩; β m 为等效弯矩系数; 弯矩放大系 数 1 0.2 P PE . Am ≈ 1 P PE 对于弹性压弯构件, 根据各种荷载作用和支撑情况, 可以计算出跨中弯矩 M max 的表达通式 β mM (3.12) M max = 1 P PE 再考虑初始缺陷的影响, 假定各种缺陷的等效初弯曲呈跨中挠度为ν 0 的正弦曲线, 则在任意横 向荷载或端弯矩作用下跨中总弯矩应为 β M + Pν 0 (3.13) M max = m 1 P PE 当压弯构件长度中点截面边缘纤维达到屈服时, 其应满足 P β m M + Pν 0 + = fy A (1 P PE )W 令( 3. 14)中 M = 0 ,则得到有初始缺陷的轴心压杆边缘纤维屈服时的表达式 P0 P0ν 0 + = fy A (1 P0 PE )W 因为 P0 = Af y ( 为轴心压杆稳定系数) ,则由式( 3. 15 )得 (3.14) (3.15) ν 0 = 11 PE A 将式( 3. 16 )代入( 3. 14 ),整理得由边缘纤维屈服导出的相关公式 β mM P + = fy A W (1 P PE ) 其中等效弯矩系数 β m 取值见表 3.1. 3.1.2 压弯构件平面内弹塑性弯曲失稳 从图

3.3 可以看出, 当压弯构件截面边缘纤维开 始屈服, 构件进入弹塑性阶段后, 随着外荷载的增加, 截面弹性区越来越小, 构件抗弯刚度降低, 变形加快, 以至构件抗弯能力增加小于外力作用效应的增加, 达 到极限状态时(图 3.3 极值点 B) ,内外力开始无法 平衡, 构件发生平面内弹塑性整体失稳. 由于压弯构件的截面形状, 尺寸和外力作用方式 等不同, 弯曲失稳时构件塑性发展的范围可能只出现 在图 3.6 (a) 所示的阴影区, 即弯曲凹面受压的一侧; 也可能如图 3.6(b)所示,

在受压凹面和受拉凸面同 时出现塑性区; 对单轴对称截面压弯构件, 塑性区也 可能只出现在受拉凸面的一侧, 图 3.6(c)所示. 1 Af y W (3.16) (3.17) 图 3.6 压弯构件弯曲失稳的塑性区分布 压弯构件的极限荷载求解比较困难, 一般情况下可用数值积分法得到数值解, 但如果截面形 状比较简单, 不考虑初弯曲和较复杂的残余应力分布影响时, 经简化后也可用解析法得到近似解. 56 表 3.1 等效弯矩系数 β m 值 1. 解析法 对于轴压力 P 和两端相同弯矩 M 共同作用的两端简支压弯构件 (图 3.7) 用 Jezek 解析法[18] , 求解可以求出精确度比较高的极限荷载. 其假设为: (1) 材料为理想的弹塑性体; (2) 构件的变形曲线为正弦曲线的一个半波. 图 3.7a 是矩形截面的压弯构件, 在轴力 P 和端弯矩 M 共同作用下, 平面内弹塑性弯曲失稳 时构件截面的塑性有两种类型: 只出现在受压区, 如图

3.7b 阴影部分所示, 截面弹性区高度为 he , 细长构件常属此类; 另一类为受压, 受拉区均出现塑性区, 图 3.7e 所示, 短粗构件常属此类. 下面分别加以讨论: 1) 第一种情况:塑性区仅出现在受压区(图 3.7b) 图 3.7c 、图 3.7d 分别为第 1 种情况截面的应变和应力图. 由应力图可以分别得出轴线方向 力和力矩的平衡方程: 2 Py P 1 P = δ y A δ y + δ t bhe 或 δ y + δ t = (3.18) 2 bhe ( ) ( ) 57 图 3.7 矩形截面压弯构件中央截面的应变和应力 M + Pv = 由上式可解出弹性区高度 1 (δ y + δ t )bhe h he 2 2 3 3h 3(M + Pν ) 2 Py P (3.19) he = (3.20) 式中, Py = Aδ y ,表示轴心受压时全截面屈服压力. 由应变图知曲率 Φ= ε y + ε t he = δ y +δ t Ehe = 2(Py P ) Ebhe2 (3.21) 根据变形曲线假定, 挠曲线为 y = ν sin (π x l ) 中央截面处的曲率为 由式(3.21)式( 3. 22 )知 (3.22) (3.23) Φ = y ′′(l 2 ) = vπ 2 / l 2 l Ebhe2 将( 3. 20 )代入( 3. 22 )后, 得到构件压力 P 与挠度 v 的函数关系 h P ν 1 2 Py 由极值条件 ν π 2 2 = 2(Py P ) (3.24) M + Pν 2l 2 Py 1 P = 2 Py 9bπ E Py 2 3 (3.25) dP dν = 0 ,得 ν = 将式( 3. 26 )代入( 3. 25)后, 得 1 Py h P M 1 3 P 2 Py Py (3.26) 58 1 2M P = 2 × bh 3 1 (3.27) 12 l hPy (1 P Py ) 1 1 由于 P = 0 时, 截面边缘纤维开始屈服时的弯矩 M y = bh 2δ y = Py h ,且全截面的惯性矩 6 6 1 I x = bh 3 ,则构件在平面内弯曲失稳的弹塑性极值荷载 12 π 2E 3 M (3.28) Pu = 1 l 2 3M y (1 Pu Py ) 将式( 3. 26 )代入( 3. 20),得情况 1 的弹性区高度 M he = h 1 (3.29) 3M y (1 Pu Py ) 则( 3. 28 )可以写成 3 π 2 EI x he π 2 EI ex (3.30) Pu = = l2 h l2 式中, I ex 是弹性区截面惯性矩, 说明塑性发展使构件抗弯刚度下降至 EI ex , 极限荷载与以弹性 区

为截面的轴心受压构件的欧拉临界力相当. 塑性区出现第一种情况的条件是图

3.7 d 中截面受拉侧的应力 δ t ≤δ y , 由式( 3. 18 )可以得出 π 2 EI x 3 he ≥ (1 Pu Py )h (3.31) 也可写作 Pu Py ≥ M 3M y 1 Pu Py ( ) (3.32) 2) 第 2 种情况:塑性区同时出现在受压, 受拉区(图 3.7 e) 出现第 2 种情况的条件为 M Pu Py < 3m="" y="" 1="" pu="" py="" (="" )="" (3.33)="" 根据图="" 3.7g="" 所示的应力分布,="" 可以分别列出轴线压力和力矩平衡方程="" p="Py" bhe="" δ="" y="" 2bcδ="" y="" 由应变图="" 3.7f="" 知曲率="" (3.34)="" (3.35)="" m="" +="" pν="bheδ" y="" (h="" 2="" he="" 3="" c="" )="" +="" 2bcδ="" y="" (h="" 2="" c="" 2="" )="" he="" ehe="" l2="" 联立式(="" 3.="" 34)="" 、(="" 3.="" 35="" )="" 、(="" 3.36="" )可得到="" p="" 与="" ν="" 之关系="" 2="" p="" 2="" m="" +="" pν="" l="" 4δ="" y="" 2="" h="" ν="" {="" 1="" }="4" py="" py="" 3hπ="" 4="" e="" dv="" 由极值条件="0" ,得="" dp="" py="" h="" p="" ν="1" 3p="" 2="" py="" 2="" φ="2ε" y="2δ" y="ν" π="" 2="" (3.36)="" (3.37)="" 2m="" py="" (3.38)="" 将式(="" 3.="" 38="" )代入式(="" 3.="" 37="" ),整理后得="" 59="" p="" [1="" u="" pu="P" l2="" y="" 由式(="" 3.="" 36="" )="" 、(="" 3.="" 38="" )="" 、(="" 3.="" 39="" )得到="" π="" 2="" ei="" x="" 2m="" ]3="" 3m="" y="" 2="" 2="" (3.39)="" he="h" 1="" pu="" py="" (="" )="" 3="" 2m="" 3m="" y="" (3.40)="" 则式(="" 3.="" 39="" )可以写作="" pu="π" 2="" ei="" x="" he="" l2="h" π="" 2="" ei="" ex="" l2="" (3.41)="" 式(="" 3.="" 41="" )与式(="" 3.="" 30="" )="" 的表达形式一致.="" 关于压弯构件的平面内弹塑性稳定分析,="" 除了简明的="" jezek="" 方法外,="" 还有较精确的数值积分="" 法.="" 2.="" 数值积分法="" 上述="" jezek="" 方法由于先假定压弯构件的变形曲线,="" 此曲线与实际的变形曲线有误差,="" 因此不="" 可能建立各个截面的力平衡方程,="" 而只能建立弯矩最大截面处的内外力平衡方程.="" 在分析中也没="" 有考虑残余应力等初始缺陷的影响.="" 由于计算中简化较多,="" 解析解的精度有待提高,="" 可以用数值="" 法确定压弯构件的极限荷载.="" 数值法有多种,="" 数值积分法是常用的一种.="" 数值积分法可分为二步计算:="" 首先根据截面的内力平衡条件建立弯矩="" m="" ,="" 压力="" p="" 和曲率="" φ="" 之="" 间的关系;="" 然后根据构件的变形曲线建立挠度,="" 转角和曲率之间的关系,="" 由于曲率与外力矩相对="" 应,="" 故可通过同一截面的曲率建立压力与挠度的关系,="" 通过分级加载得到压力="" p="" 与构件中点挠度="" ν="" m="" 的对应函数关系,="" 利用极值条件即可得到压弯构件的极限荷载.="" 以图="" 3.8(a)为例,="" 说明数值积分法的计算过程.="" 已知截面尺寸、构件长度、荷载作用条件="" m="" p="e" ,残余应力分布如图="" 3.8(b)="" 所示,="" 残余="" 压应力、拉应力峰值分别为="" δ="" rc="" 和="" δ="" rt="" ,材料为理想弹塑性体.="" 图="" 3.8="" 压弯构件数值积分法示例="" 1)="" 建立截面的="" m="" p="" φ="" 关系="">

3.9(a)表示划分为很多单元的工形截面, 单元的面积为 Ai , 截面任一点的应变 ε i 是轴 向应变 ε 0 、弯曲应变 Φz i 和残余应变 ε ri = δ ri E 三部分的代数和(如图 3.9(b)、(c)所示) , 即 ε i = ε 0 + Φz i + ε ri (a) 60 图 3.9 截面的应变 当截面处

于弹性状态时, 应力 δ i = Eε i ,根据内力平衡条件 M = ∫A δ i z i dA = ∫A E (ε 0 + Φz i + ε ri )z i dA = EΦ ∫A z i2 dA = EI x y ′′ P = ∫A δ i dA = ∫A E (ε 0 + Φz i + ε ri )dA = Eε 0 A (b) (c) 由式(c)可知, 当截面处于弹性状态时, 压弯构件和受弯构件一样, 弯矩 M 与曲率 Φ 成正比, 而与轴线压力 P 无关. 但在弹塑性状态, 因各截面塑性发展程度不同, M P Φ 相关. 在弹塑性状态时, 若以 ε y = δ y E 表示屈服应变, 任一单元面积 Ai 上的应力均取平均值, 则有 δ i = Eε i δ i =δ y δ i = δ y 当 ε y ≤ ε i ≤ ε y 时 当 当 ε i >ε y 时 ε i < ε="" y="" 时="" (d)="" 截面的轴向压力="" p="" 和弯矩="" m="" 分别为="" p="∑" δ="" i="" ai="" a="" m="∑" δ="" i="" ai="" z="" i="" a="" (e)="" 联合(a)、(d)="" ,通过对式(e)数值积分即可得到构件在弹塑性状态的="" m="" p="" φ="" 关系.="" 具="" 体算法见如下框图="" 图="" 3.10="" 电算框图="" 61="" 2)求解压弯构件的极限荷载="" pu="" 以图="" 3.11="" 所示两端铰接,="" 几何条件和荷载作用均对称的压弯构件为例,="" 具体求解过程见框="" 图="" 3.12.="" 图="" 3.11="" 两端铰接压弯构件="" 图="" 3.11(a)中所示压弯构件在给定一个轴力="" p1="" 情况下,="" 端部挠度="" y="" 0="0,而转角" 0="" 未知,="" 使其满足构件中点的转角="" m="0" 即可,="" 若给定的="" 0="" 不能使="" m="" 足="" 不过可以先给定一个="" 0="" 的初始值,="" 够小(如="" m=""><10 5="" )="" ,则调整="" 0="" 重新迭代,="" 直至="" m="" 足够小,="" 满足计算精度要求.="" 这样就可以得="" 到与给定轴力="" p1="" 对应的构件中点的挠度="" v="" m1="" 值,="" 如图="" 3.11(b)所示.="" 同理,="" 可以得到不同的轴力="" p="" 对应的构件中点的挠度="" ν="" m="" 值,="">

3.11(b)所示 的 P ν m 曲线, 其极限点 B 对应的 P 即为极限荷载 Pu . 对不同的荷载作用, 数值积分的思路相同, 但具体计算细节有所不同. 通过理论求解和试验 分析压弯构件在平面内的极限荷载, 才可以推演出压弯构件的稳定设计公式. 62 图 3.12 压弯构件极限荷载电算框图 3.1.3 压弯构件弯矩作用平面内的稳定理论在设计中的应用 压弯构件在弯矩作用平面内的整体稳定计算通常采用两个计算准则, 即边缘纤维屈服准则和 极限承载力准则. 1. 边缘纤维屈服准则 边缘纤维屈服准则以弹性分析为基础, 以弯矩最大截面边缘纤维屈服作为计算准则. 这一准 63 则比较适用于冷弯薄壁型钢压弯构件, 因为这类构件的边缘纤维屈服荷载非常接近于构件的极限 荷载; 该准则也用于格构式压弯构件绕虚轴弯曲的稳定计算. 参照式(3.17) , 给合压弯构件弯矩作用平面内的稳定概念, 可以得到按边缘纤维屈服准则 导出的相关公式 β mx M x P + = fy (3.42) x A P W1x 1 x

PEx 式中 x 为弯矩作用平面内轴心受压构件的整体稳定系数; W1x 为受压最大纤维的毛截面抵抗矩; β mx 为等效弯矩系数, 参见表 3.1. 将式(3.42)写成设计公式, 即 β mx M x P + ≤f (3.43) x A P W x 1 x PEx 式中 f 为钢材屈服强度设计值.

2. 极限承载力准则 一般钢结构中的压弯构件当截面最大纤维刚开始屈服时尚有较大的强度储备, 即可以容许截 面塑性有一定发展, 因此应该以 弹塑性稳定理论为基础, 以失稳时的极限荷载为计算准则. 压弯构件的初偏心和初弯曲对构件的影响性质上相同, 因此在制定规范时考虑构件存在 l 1000 的初弯曲(即初弯曲的矢高为构件长度 l 的 1/1000) , 考虑实测的残余应力分布, 用数值方 法计算出近 200 条压弯构件的极限承载力曲线. 将用数值方法得到的压弯构件极限承载力 Pu 与 用边缘纤维屈服准则导出的相关公式(3.42)中的轴心压力 P 比较后发现, 对于短粗实腹杆, 式 (3.42)偏于安全; 而对细长实腹杆, 式(3.42)偏于不安全. 因此, 规范借用了弹性压弯构件 边缘纤维屈服准则计算公式的形式, 同时考虑截面塑性发展和二阶弯矩, 最后提出了一近似相关 公式, 即规范所采用的实腹式压弯构件弯矩作用平面内的稳定计算公式 β mx M x P + ≤ f (3.44) xA γ RP γ xW1x 1 0.8 PEx 式中 P ——所计算构件段范围内的轴向压力; M x ——所计算构件段范围内的最大弯矩; x ——弯矩作用平面内的轴心受压构件的稳定系数; W1x ——弯矩作用平面内较大受压纤维的毛截面抵抗矩; PEx——欧拉临界力; γ R — —抗力分项系数, 对 Q235 钢,γ R = 1.087 ,对 Q345,Q390,Q420 钢,γ R = 1.111 ; β mx ——等效弯矩系数, 参见表 3.1. 对于 T 型钢, 双角钢 T 形等单轴对称截面压弯构件, 当弯矩作用于对称轴平面且使较大翼 缘受压时, 构件失稳时出现的塑性区除存在受压区屈服和受压, 受拉区同时屈服两种情况外, 还 可能在受拉区首先屈服而导致构件失去承载能力, 因此除了按式(3.44)计算外, 还应按下式计 算: 64 P A 式中 β mx M x γ P γ xW2 x 1 1.25 R PEx ≤ f (3.45) W2 x ——受拉侧最外纤维的毛截面抵抗矩; γ x ——与 W2 x 相应的截面塑性发展系数. 其余符号同式(3.44) , 上式第二项分母中的 1.25 也是经过与理论计算结果比较后引进的修 正系数. 3.2 压弯构件平面外失稳 如图 3.1(c)所示, 当压弯构件没有设置侧向支撑时, 在外荷载 P 尚未达到平面内弯曲失稳的 临界荷载 Pu 之前, 就可能导致压弯构件发生空间的弯扭失稳, 也称平面外弯扭屈曲. 当构件长 细比较大时, 有可能在弹性阶段失稳; 在长细比较小等情况下也有可能在弹塑性阶段失稳. 对于外力

作用和端部支撑条件较简单的压弯构件, 可以用平衡法求解弯扭屈曲荷载的精确 解; 如果外力作用或端部支撑条件较复杂, 可以用能量法求解. 在弹塑性阶段发生弯扭屈曲的压 弯构件, 采用数值法可以获得较高的求解精度. 3.2.1 压弯构件的弹性弯扭失稳 压弯构件的弹性弯扭失稳 1. 平衡法求解单轴对称截面压弯构件的弹性弯扭屈曲荷载 以两端简支单轴对称截面压弯构件(图 3.13) 为例, 说明平衡法求解弹性弯扭屈曲荷载的过 程. 图 3.13 压弯构件弯扭变形及受力 65 分析中采用两个坐标系, 即截面的固定坐标系 oxyz 和移动坐标系 o ′ ξ (图

3.13) , 且 采用如下假设: ① 构件为弹性体; ② 发生弯曲与扭转变形时, 截面的形状不变; ③ 弯曲与扭转变形微小; ④ 构件是无缺陷的等截面直杆; ⑤ 在弯矩作用平面内抗弯刚度很大, 屈曲前平面内的弯曲变形对弯扭屈曲的影响可以忽略. 参考第二章 2.4 节中单轴对称截面轴心受压构件弹性弯扭失稳建立平衡微分方程的过程, 可 以分别得到绕ξ 轴和 轴 的弯矩平衡方程. EI xν ′′ + Pν + M x = 0 (3.46) EI y u ′′ + Pu + (M x + Py 0 ) = 0 (3.47) 由图 3.13a 所示受力条件和坐标系, 如以压应力为正值, 则构件截面上任一点的正应力 P M y (3.48) δ = x A Ix Wagner 效应系数为 M P 2 2 K = ∫A (δ + δ r )ρ 2 dA = ∫A x 2 + ( y y 0 ) dA x ∫A y x 2 + ( y y 0 ) dA + ∫A δ r x 2 + y 2 dA A Ix [ ] [ ] ( ) = 式中 : M P 2 I x + I y + Ay 0 x A Ix ( ) [∫ y(x A 2 + y 2 )dA 2 I x y 0 + ∫A δ r (x 2 + y 2 )dA = ρ i 0 2 β y M x + R 2 ] 2I x 是截面的几何性质参数, β y 为不对称截面常数, 对于单轴对称工形截面, β y 中前一项数值常比 y 0 小得多, 对图 3.13c 所示坐标系, 剪心矩 y 0 是正值, 则 β y 将是负值. 外弯矩 M x 在纵轴 方向的分量为 i0 2 = (I x + Iy ) A+ y , 2 0 β y ∫ y (x = A 2 + y 2 )dA y 0 , R = ∫A δ r (x 2 + y 2 )dA . i 0 和 β y 都 M x sin ≈ M x = M x u ′ 切力 Pu ′ 产生的扭矩从图 3.13c 知为 则在 方向总的非均匀扭矩 扭矩平衡方程为 Pu ′ y 0 cos ≈ Py 0 u ′ 2 M = Pi 0 2 β y M x + R ′ + M x u ′ + Py 0 u ′ EI w ′′′ + Pi0 2 β y M x GI t + R ′ + (M x + Py 0 )u ′ = 0 2 ( ) (3.49) (3.50) ( ) 联立方程(3.46)(3.47)和(3.50) , ,得到适合任何边界条件的压弯构件微分方程组 EI x ν IV + Pν ′′ = 0 (3.51) EI w IV + Pi0 2 β y M x GI t + R ′′ + (M x + Py 0 )u′′ = 0 2 ( EI y u IV + Pu′′ + (M x + Py0 ) ′′ = 0 ) (3.52) (3.53) 由于忽略了屈曲前

平面内弯曲变形对弯扭屈曲的影响, 因此方程(3.51)与后面两方程解耦, 只能用于描述平面内荷载—挠度弹性曲线. 后两个方程是耦联的, 引入边界条件, 可联立求解得 到构件的弹性弯扭屈曲荷载 Pyw . 对两端简支的压弯构件, 满足边界条件的变形函数为 π z π z = c 2 sin u = c1 sin , l l 66 将它们代入方程(3.52)(3.53) , ,得 (M x + Py 0 )c 2 = 0 Py P c1 2 2 (M x + Py 0 )c1 + i0 Pw i0 P 2 β y M x c 2 = 0 ( )

[ ( )] (3.54) 式中: p y = π 2 EI y l 2 , Pw = 2 1 π EI w + GI t R . 2 2 i0 l 由 c1 和 c 2 有非零解的条件为系数行列式为零, 可以得到屈曲方程 (P y P ) i 02 Pw (i 02 P 2 β y M x ) (M x + Py 0 ) = 0 2 [ ] (3.55) 方程(3.55)中的 M x 以弯矩使形心以上的负方向受压时为正, 受拉时为负; 而偏心矩 e y 符号与 y 轴正负一致, 由图

3.13a 知 M x = Pe y ,代入方程(3.55) ,则有 (P y P ) i02 Pw P (i02 + 2 β y e y ) ( y 0 e y ) P 2 = 0 2 [ ] (3.56) 2 解之得弹性弯扭屈曲荷载 Pyw = i 02 (Py + Pw ) + 2 β y e y Py [i (P 2 0 2 i02 + 2 β y e y ( y 0 e y ) y [ + Pw ) + 2 β y e y Py ] 2 4i02 Py Pw i 02 + 2 β y e y ( y 0 e y ) 2 ] [ ] (3.57) 相应的弯扭屈曲应力 δ yw = Pyw A = π 2E λ 2 yw (3.58) 式中 λ yw 为计算弯扭屈曲应力的换算长细化 λ yw = λ y 其中 w = 2 2 w 2 + i0 + 2β y e y 2w 2 2 w 2 + i0 + 2β y e y + 2w 2 i 2 + 2β y e y y 0 e y 0 w2 2

( ) ( 2 ) 2 (3.59) A l2 对双轴对称截面压弯构件, 因 y 0 = 0, β y = 0, i02 = (I x + I y )

A ,则方程(3.55)为 λ 2y I ω + GI t R . π 2E (P y P )(Pw P ) M x2 i02 = 0 (3.60) 解出弯扭屈曲荷载 1 Pyw = Py + Pw 2 (P y + Pw ) 2 2 2 4 Py Pw M x l 0 ( ) (3.61) 对无对称轴截面压弯构件, 开始施加压力 P, 构件就产生双向弯曲变形和扭转, 因此属于极 值点失稳问题. 对此类问题用平衡法求解析解较困难, 一般采用能量法[19]或数值法求解其极限 荷载. 【例题 3.1】 已知两端简支的单轴对称 T 形截面压弯构件的长度 例题 为 4m, 构件的两端作用有弯矩 M x = 10kN m , 截面尺寸如图 3.14 . 钢 材 δ y = 23.5 kN cm 2 , E = 2.06 × 10 4 kN / cm 2 , G = 7.9 × 10 3 kN / cm 2 , 按理想弹塑性体计算, 不计残余应力. 构 件在弯矩作用平面内的极限荷载 Pu = 735kN .求此压弯构件的屈 曲荷载. 图 3.14 T 形截面压弯构件 67 [解]: 1) 计算截面的几何性质 截面积 A=2 × 1 × 20=40cm 2 1 × 20(10 + 0.5) y0 = =

5.25cm 剪心矩 2 × 20 1 惯性矩 I x = 1 × 20 × 5.25 2 + × 1 × 20 3 + 1 × 20 × 5.25 2 = 1769.2cm 4 12 1 3 I y = × 1 × 20 = 666.7cm 4 12 1 I k = 2 × × 20 × 13 = 13.33cm 4 , Iw = 0 3 Ix 对翼缘边缘抵抗矩 W1x = = 307.07cm 3 5.25 + 0.5 I W2 x = x =

116cm 3 对腹板边缘抵抗矩 15.25 Ix + Iy 2 i02 = + y 0 = 88.46cm 2 A ∫ y (x A 2 7000 ( 5.25) = 1.98 + 5.25 = 7.23cm 2I x 2 × 1769.2 2) 计算 M x = 10kN m 时构件的弯扭屈曲荷载 Pyw β y = ∫ y (x A + y 2 )dA = t ∫ 4.75 y 3 dy + 2t ∫0 ( 5.25)(x 2 +

5.25 2 )dx = 7000cm 5 15.25 10 2 + y 2 )dA y0 = Py = π 2 EI y l 2 = π 2 × 2.06 × 10 4 × 666.7 / 400 2 = 847.2kN Px = π 2 EI x / l 2 = π 2 × 2.06 × 10 4 × 1769.2 / 400 2 = 2248.2kN 3 1 2 Pw = 2 (π 2 EI w l w + GI k ) = GI k i02 = 7.9 × 10 × 13.33 = 1190.4kN 88.46 i0 由式(3.55)得 60.9 P 2 184206 P + 100463044 = 0 解出 (847.2 P )[88.46 × 1190.4 (88.46 P 2 × 7.23 × 10 × 10 2 )] [10 × 10 2 + ( 5.25P )]2 = 0 Pyw = 713.86kN 3) 确定屈曲荷载 由于翼缘边缘纤维的压应力 713.86 10 × 10 2 1 + 0.234 × 713.86 2248.2 δ 1 = + =17.85+5.12= 22.97 kN cm 2 < δ="" y="23.5" kn="" cm="" 2="" 713.86="" 40="" 307.71="">

范文三：　弹性模量计算公式

文档可能在WAP 端浏览体验不佳。建议您优先选择TXT，或下载源文件到本机查看。 第三章 压弯构件的失稳 轴力偏心作用的构件或同时受轴力和横向荷载作用的构件称为压弯构件. 由于压弯构件兼有 受压和受弯的功能,又普遍出现在框架结构中,因此又称为梁柱. 钢结构中的压弯构件多数是截面至少有一个对称轴, 且偏心弯矩作用在对称平面的单向偏心 情况.对单向偏心的压弯构件,有可能在弯矩平面内失稳,即发生弯曲失稳;也有可能在弯矩作 用平面外失稳,即弯扭失稳.其弯曲失稳为第二类稳定问题,即极值点失稳;其弯扭失稳对理想 的无缺陷的压弯构件属于第一类稳定问题,即分支点失稳,但对实际构件则是极值点失稳. 对理想的两端简支的双轴对称工形截面压弯构件,在两端作用有轴线压力 P 和使构件产生 同向曲率变形的弯矩 M,如果在其侧向有足够的支撑 (如图 3.1(b)),构件将发生平面内的弯 曲失稳,其荷载― 挠度曲线如图 3.2(a)中曲线 a,失稳的极限荷载为 Pu,属于极值点失稳. 图 3.1 两端简支理想压弯构件 图 3.2 压弯构件荷载变形曲线 如果在侧向没有设置支撑(如图 3.1(c),则构件在荷载 P 未达到平面内极限荷载 Pu 时, ) 可能发生弯扭失稳,即在弯矩作用平面内产生挠度 v,在平面外剪心产生位移u,并绕纵轴产生 扭转角 (如图 3.1(d),其荷载-变形曲线如图 3.2(b)中曲线 b,属于分支点失稳,失稳 ) 的分荷载为 Pyw, ,且 Pyw 3. 1 压弯构件平面内失稳 对压弯构件, 当弯矩作用平面外有足够多支撑可以避免发生弯扭失稳时, 若失稳则只可能发 生平面内弯曲失稳. 当用弹性理论分析理想压弯构件的荷载挠度关系,可以得到图 3. 3 中的二阶弹性曲线 b,它 以轴心受压弯构件的分岔点荷载 PE 处引出的水平线 a 为渐近线. 实际压弯构件存在初始缺陷(残余应力、几何缺陷), 材料为弹塑性体. 如按弹塑性理论分析, 荷载挠度曲线将是图中曲线 OABC.曲线上 A 点标志着杆件中点截面边缘开始屈服,对应的荷 载为 Pe,随后塑性向截面内部发展,构件变形快速增加,形成 OAB 上升段,构件处于稳定平衡 状态;B 点为曲线的极值点,对应的荷载 Pu 为构件在弯矩作用平面内失稳的极限荷载;到达 B 点以后,由于弹性区缩小到导致构件抵抗力矩的增加小于外力矩的增加程度,出现下降段 BC, 52 构件处于不稳定平衡状态. 由失稳全过程可以看出实际压弯构件在弯矩作用平面内的弯曲失稳属 于二阶弹塑性分析的极值点失稳,不能用弹性理论和平衡微分方程求解极限荷载 Pu,而可用数 值积分法通过得出荷载挠度曲线后求得极限荷载. 压弯构件平面内弯曲失稳的

弹性分析虽然不能求出极限荷载, 但它是弹塑性分析的基础, 因 此有必要先研

究压弯构件平面内弹性失稳. 图 3 .3 压弯构件荷载挠度曲线 3.1.1 压弯构件平

面内弹性弯曲性能 在第二章讨论初始几何缺陷对轴心受压构件稳定性能的影响

时,对图 2.13 所示有偏心的轴 心受压杆已作过分析,即当作偏心压弯构件得出

了荷载 P 与构件中点挠度δ 之间的关系曲线. 从式(2.48)中可以看出,若假设材

料是无限弹性体,则当δ ??时,P?PE,即临界荷载 P 以欧 拉荷载 PE 为极值.然

而实际材料都是有限弹性的,由于压弯构件平面内弯曲失稳时,构件为弹 塑性工

作状态,因此弹性分析只有理论意义. 下面仅讨论两端铰接受轴向压力和平面内

. 1. 横向均布荷载作用的横向荷载共同作用的弹性压弯构件的内力与变形 性能

压弯构件 横向均布荷载作用的压弯构件 图 3.4(a)所示 为在均布荷载 q 作用

下两端铰接的压弯构件.假定材料完全弹性,取图 3. 4(c) 所示隔离体, 在距左端

x 处截面的内力矩 M f = EIy ′′ ,外力矩 M e = Py + qx (l x ) 2 ,平衡方程 为 令 k

= P EI ,则 2 EIy ′′ + Py = qx(l x ) 2 qx( x l ) 2 EI 2 方程 (3. 1)的特解可写作 y = c1

x + c 2 x + c 3 ,代入方程( 3. 1 ) ,有 y ′′ + k 2 y = (3.1) (Pc1 q 2)x 2 + (Pc 2 + ql 2)x

+ Pc3 + 2 EIc1 = 0 上式是恒等式,故 53 c1=q?(2P) ,c2= -q l ?(2P) 2 ,c3= -EIq?P 2 方

程( 3. 1 )对应的齐次线性方程 y〃+k y =0 的通解可写作 y =Asin kχ +Bcos kχ , 则方程 ( 3. 1 ) 的通解为 2 2 y= Asin kχ +Bcos kχ + qχ ?(2P)-q l χ ?(2P)-EIq/ P (3.2) 由边界条件 y(0) =0 , y( l )=0 得 A= EIq?P tg (κ l ?2) , 2 B=EIq?P 2 则 q kl qx tg sin kx + cos kx 1 2 (l x ) k EI 2 2k EI 构件在 x = l 2 处有最大挠度 y max , 令 u

= kl 2 ,可得 y= 4 (3.3) y max = ql 4 1 cos u ql 4 16 EIu 4 cos u 32 EIu 2 12(2 sec u u

2 2) = y0 5u 4 (3.4) 式中: y 0 = 5ql 4 (384 EI ) 是均布荷载作用下简支梁的最大挠

度,即当 P=0 时,由式 ( 3. 4 ) 求得 的最大挠度.式( 3. 4 ) 中括号内的值为考虑

轴线压力后最大挠度的放大系数. 图 3.4 均布荷载作用的压弯构件 将 sec u 展

开成幂级数,有 sec u = 1 + 式中 1 2 5 4 61 6 277 8 u + u + u + u + 2 24 720 8064

u= kl l = 2 2 P π = EI 2 P PE 则式( 3. 4 )可写成 y max = y 0 1 + 1.034(P PE ) + 1.0038(P PE ) + ? y 0 2 [ ] 1 1 P PE (3.5) 式中 Am = 1 / (1 P / PE ) 是最大挠度的

放大系数. 构件中点的最大弯矩为 = Am y0 54 1.028 P PE M max = ql 2 8 + Py max = M 0 1+ 1 P PE β mM = 1 P P = Am M 0 E (3.6) 式中 M 0 = ql 2 8 是均布荷

载作用下简支梁跨中的最大弯矩; β m 为等效弯矩系数; Am 为弯矩放大 系数,

用以考虑轴压力 P 产生的二阶效应. 2. 横向集中荷载作用的压弯构件 由图

3.5(c)知,当 0< x="" l="" 2="" 时,平衡方程为="" eiy="" ′′="" +="" py="Qx" 2="" 令="" k="" 2="P" (="" ei="" )="" ,="" 则="">

解为 y ′′ + k 2 y = Qx (2 EI ) (3.7) 3 Ql (tgu u ) = Ql 33 (tgu u ) = y0 3(tgu3 u ) (3.9)

4 Pu 48EI u u 式中 y 0 = Ql 3 (48 EI ) 是集中荷载 Q 作用在跨中时简支梁的最

大挠度,3(tgu u ) u 3 是有轴压力作 用时最大挠度放大系数. 将 tgu 展成幂级数

y = A sin kx + B cos kx Qx (2 P ) Q 引入边界条件 y (0 ) = 0 , y ′(l 2) = 0, 得 B = 0, A = sec (kl 2), 则通解 2 Pk Q kl y= sec sec kx kx 2 Pk 2 令 u = kl 2, 当 x = l 2 时,跨中最大挠度为 ymax = (3.8) tgu = u + u 3 3 + 2u 5 15 +17u 7 315 + 将 u = kl 2 = π 2 P PE 代入,则式( 3. 9 )可改写为 y max = y 0 1 + 0.987(P PE ) + 0.986(P PE )

+ ? y 0 2 [ 图 3.5 跨中集中荷载作用的压弯构件 ] 式中 1 (1 P / PE ) 为最大挠

度放大系数. 跨中最大弯矩为 1 1 P PE (3.10) M max = Ql 4 + Py max = Ql Pl 2 1

+ 4 12 EI (1 P PE ) 55 1 0.178 P PE β m M 0 = =M0 (3.11) 1 P P 1 P P = Am M 0 E E

式中 M 0 = Ql 4 是集中荷载作用下简支梁最大弯矩; β m 为等效弯矩系数;弯矩

放大系 数 1 0.2 P PE . Am ? 1 P PE 对于弹性压弯构件,根据各种荷载作用和支

撑情况,可以计算出跨中弯矩 M max 的表达通式 β mM (3.12) M max = 1 P PE 再考虑初始缺陷的影响,假定各种缺陷的等效初弯曲呈跨中挠度为ν 0 的正弦曲

线,则在任意横 向荷载或端弯矩作用下跨中总弯矩应为 β M + Pν 0 (3.13) M max = m 1 P PE 当压弯构件长度中点截面边缘纤维达到屈服时,其应满足 P β m M + Pν 0 + = fy A (1 P PE )W 令( 3. 14)中 M = 0 ,则得到有初始缺陷的轴心压杆边缘

纤维屈服时的表达式 P0 P0ν 0 + = fy A (1 P0 PE )W 因为 P0 = Af y ( 为轴心压

杆稳定系数) ,则由式( 3. 15 )得 (3.14) (3.15) ν 0 = 11 PE A 将式( 3. 16 )代入( 3.

14 ),整理得由边缘纤维屈服导出的相关公式 β mM P + = fy A W (1 P PE ) 其中

等效弯矩系数 β m 取值见表 3.1. 3.1.2 压弯构件平面内弹塑性弯曲失稳 从图

3.3 可以看出,当压弯构件截面边缘纤维开 始屈服, 构件进入弹塑性阶段后, 随

着外荷载的增加, 截面弹性区越来越小, 构件抗弯刚度降低, 变形加快, 以至构

件抗弯能力增加小于外力作用效应的增加, 达 到极限状态时(图 3.3 极值点 B) ,

内外力开始无法 平衡, 构件发生平面内弹塑性整体失稳. 由于压弯构件的截面

形状, 尺寸和外力作用方式 等不同, 弯曲失稳时构件塑性发展的范围可能只出

现 在图 3.6 (a) 所示的阴影区, 即弯曲凹面受压的一侧; 也可能如图 3.6(b)所示,

在受压凹面和受拉凸面同 时出现塑性区;对单轴对称截面压弯构件,塑性区也 可能只出现在受拉凸面的一侧,图 3.6(c)所示. 1 Af y W (3.16) (3.17) 图 3.6 压弯构件弯曲失稳的塑性区分布 压弯构件的极限荷载求解比较困难, 一般情况下可用数值积分法得到数值解, 但如果截面形 状比较简单, 不考虑初弯曲和较复杂的残余应力分布影响时, 经简化后也可用解析法得到近似解. 56 表 3.1 等效弯矩系数 β m 值 1. 解析法 对于轴压力 P 和两端相同弯矩 M 共同作用的两端简支压弯构件 (图 3.7) 用 Jezek 解析法[18] , 求解可以求出精确度比较高的极限荷载.其假设为: (1) 材料为理想的弹塑性体; (2) 构件的变形曲线为正弦曲线的一个半波. 图 3.7a 是矩形截面的压弯构件, 在轴力 P 和端弯矩 M 共同作用下,平面内弹塑性弯曲失稳 时构件截面的塑性有两种类型: 只出现在受压区, 如图 3.7b 阴影部分所示, 截面弹性区高度为 he , 细长构件常属此类; 另一类为受压,受拉区均出现塑性区,图 3.7e 所示,短粗构件常属此类. 下面分别加以讨论: 1)第一种情况:塑性区仅出现在受压区(图 3.7b) 图 3.7c、图 3.7d 分别为第 1 种情况截面的应变和应力图.由应力图可以分别得出轴线方向 力和力矩的平衡方程: 2 Py P 1 P = , y A , y + , t bhe 或 , y + , t = (3.18) 2 bhe ( ) ( ) 57 图 3.7 矩形截面压弯构件中央截面的应变和应力 M + Pv = 由上式可解出弹性区高度 1 (, y + , t )bhe h he 2 2 3 3h 3(M + Pν ) 2 Py P (3.19) he = (3.20) 式中, Py = A, y ,表示轴心受压时全截面屈服压力. 由应变图知曲率 Φ= ε y + ε t he = , y +, t Ehe = 2(Py

P ) Ebhe2 (3.21) 根据变形曲线假定,挠曲线为 y = ν sin (π x l ) 中央截面处的曲率为 由式(3.21)式( 3. 22 )知 (3.22) (3.23) Φ = y ′′(l 2 ) = vπ 2 / l 2 l Ebhe2 将( 3. 20 )代入( 3. 22 )后,得到构件压力 P 与挠度 v 的函数关系 h P ν 1 2 Py 由极值条件 ν π 2 2 = 2(Py P ) (3.24) M + Pν 2l 2 Py 1 P = 2 Py 9bπ E Py 2 3 (3.25) dP dν =

0 ,得 ν = 将式( 3. 26 )代入( 3. 25)后,得 1 Py h P M 1 3 P 2 Py Py (3.26) 58 1 2M P

= 2 × bh 3 1 (3.27) 12 l hPy (1 P Py ) 1 1 由于 P = 0 时,截面边缘纤维开始屈服时的弯矩 M y = bh 2, y = Py h ,且全截面的惯性矩 6 6 1 I x = bh 3 ,则构件在平面内弯曲失稳的弹塑性极值荷载 12 π 2E 3 M (3.28) Pu = 1 l 2 3M y (1 Pu Py ) 将式( 3. 26 )代入( 3. 20),得情况 1 的弹性区高度 M he = h 1 (3.29) 3M y (1 Pu Py ) 则( 3. 28 )可以写成 3 π 2 EI x he π 2 EI ex (3.30) Pu = = l2 h l2 式中, I ex 是弹性区截面惯性矩,说明塑性发展使构件抗弯刚度下降至 EI ex ,极限荷载与以弹性 区

为截面的轴心受压构件的欧拉临界力相当. 塑性区出现第一种情况的条件是图 3.7 d 中截面受拉侧的应力 , t ?, y , 由式( 3. 18 )可以得出 π 2 EI x 3 he ? (1 Pu Py )h (3.31) 也可写作 Pu Py ? M 3M y 1 Pu Py ( ) (3.32) 2) 第 2 种情况:塑性区同时出现在受压,受拉区(图 3.7 e) 出现第 2 种情况的条件为 M Pu Py < 3m="" y="" 1="" pu="" py="" (="" )="" (3.33)="" 根据图="" 3.7g="" 所示的应力分布,可以分别列出轴线压力和力矩平衡方程="" p="Py" bhe="" ,="" y="" 2bc,="" y="" 由应变图="" 3.7f="" 知曲率="" (3.34)="" (3.35)="" m="" +="" pν="bhe,">

y (h 2 he 3 c ) + 2bc, y (h 2 c 2 ) he Ehe l2 联立式( 3. 34) 、( 3. 35 ) 、( 3.36 )可得到 P 与 ν 之关系 2 P 2 M + Pν l 4, y 2 h ν { 1 }= 4 Py Py 3hπ 4 E dv 由极值条件 = 0 ,得 dP Py h P ν = 1 3P 2 Py 2 Φ= 2ε y = 2, y =ν π 2 (3.36) (3.37) 2M Py (3.38)

将式( 3. 38 )代入式( 3. 37 ),整理后得 59 P [1 u Pu = P l2 y 由式( 3. 36 ) 、( 3. 38 ) 、( 3. 39 )得到 π 2 EI x 2M ]3 3M y 2 2 (3.39) he = h 1 Pu Py ( ) 3 2M 3M y (3.40) 则式( 3. 39 )可以写作 Pu = π 2 EI x he l2 = h π 2 EI ex l2 (3.41) 式( 3. 41 )与式( 3. 30 ) 的表达形式一致. 关于压弯构件的平面内弹塑性稳定分析, 除了简明的 Jezek 方法外,还有较精确的数值积分 法. 2. 数值积分法 上述 Jezek 方法由于先假定压弯构件的变形曲线,此曲线与实际的变形曲线有误差,因此不 可能建立各个截面的力平衡方程, 而只能建立弯矩最大截面处的内外力平衡方程. 在分析中也没 有考虑残余应力等初始缺陷的影响.由于计算中简化较多,解析解的精度有待提高,可以用数值 法确定压弯构件的极限荷载.数值法有多种,数值积分法是常用的一种. 数值积分法可分为二步计算: 首先根据截面的内力平衡条件建立弯矩 M , 压力 P 和曲率 Φ 之 间的关系;然后根据构件的变形曲线建立挠度,转角和曲率之间的关系,由于曲率与外力矩相对 应, 故可通过同一截面的曲率建立压力与挠度的关系, 通过分级加载得到压力 P 与构件中点挠度 ν m 的对应函数关系,利用极值条件即可得到压弯构件的极限荷载. 以图 3.8(a)为例,说明数值积分法的计算过程. 已知截面尺寸、构件长度、荷载作用条件 M P = e ,残余应力分布如图 3.8(b) 所示,残余 压应力、拉应力峰值分别为 , rc 和 , rt ,材料为理想弹塑性体. 图 3.8 压弯构件数值积分法示例 1) 建立截面的 M P Φ 关系 图 3.9(a)表示划分为很多单元的工形截面,单元的面积为 Ai ,截面任一点的应变 ε i 是轴 向应变 ε 0 、弯曲应变 Φz i 和残余应变 ε ri = , ri E 三部分的代数和(如图 3.9(b)、(c)所示) , 即 ε i = ε 0 + Φz i + ε ri (a) 60 图 3.9 截面的应变 当截面处

于弹性状态时,应力 , i = Eε i ,根据内力平衡条件 M = ?A , i z i dA = ?A E (ε 0 +

Φz i + ε ri )z i dA = EΦ ?A z i2 dA = EI x y ′′ P = ?A , i dA = ?A E (ε 0 + Φz i + ε

ri )dA = Eε 0 A (b) (c) 由式(c)可知,当截面处于弹性状态时,压弯构件和受弯构件一样,弯矩 M 与曲率 Φ 成正比, 而与轴线压力 P 无关.但在弹塑性状态,因各截面塑性发展程度不同, M P Φ 相关. 在弹塑性状态时,若以 ε y = , y E 表示屈服应变,任一单元面积 Ai 上的应力均取平均值, 则有 , i = Eε i , i =, y , i = , y

当 ε y ? ε i ? ε y 时 当 当 ε i >ε y 时 ε i < ε="" y="" 时="" (d)="" 截面的轴向压力="" p="" 和弯矩="" m="" 分别为="" p="?" ,="" i="" ai="" a="" m="?" ,="" i="" ai="" z="" i="" a="" (e)="" 联合(a)、(d)="" ,通过对式(e)数值积分即可得到构件在弹塑性状态的="" m="" p="" φ="" 关系.具="" 体算法见如下框图="" 图="" 3.10="" 电算框图="" 61="" 2)求解压弯构件的极限荷载="" pu="" 以图="" 3.11="" 所示两端铰接,几何条件和荷载作用均对称的压弯构件为例,具体求解过程见框="" 图="" 3.12.="" 图="" 3.11="" 两端铰接压弯构件="" 图="" 3.11(a)中所示压弯构件在给定一个轴力="" p1="" 情况下,端部挠度="" y="" 0="0,而转角" 0="" 未知,="" 使其满足构件中点的转角="" m="0" 即可,="" 若给定的="" 0="" 不能使="" m="" 足="" 不过可以先给定一个="" 0="" 的初始值,="" 够小(如="" m=""><10 5="" )="" ,则调整="" 0="" 重新迭代,直至="" m="" 足够小,满足计算精度要求.这样就可以得="" 到与给定轴力="" p1="" 对应的构件中点的挠度="" v="" m1="" 值,="" 如图="" 3.11(b)所示.="" 同理,可以得到不同的轴力="" p="" 对应的构件中点的挠度="" ν="" m="" 值,最终可以画出图="" 3.11(b)所示="" 的="" p="" ν="" m="" 曲线,其极限点="" b="" 对应的="" p="" 即为极限荷载="" pu="" .="" 对不同的荷载作用,数值积分的思路相同,但具体计算细节有所不同.通过理论求解和试验="" 分析压弯构件在平面内的极限荷载,才可以推演出压弯构件的稳定设计公式.="" 62="" 图="" 3.12="" 压弯构件极限荷载电算框图="" 3.1.3="" 压弯构件弯矩作用平面内的稳定理论在设计中的应用="" 压弯构件在弯矩作用平面内的整体稳定计算通常采用两个计算准则,="" 即边缘纤维屈服准则和="" 极限承载力准则.="" 1.="" 边缘纤维屈服准则="" 边缘纤维屈服准则以弹性分析为基础,="" 以弯矩最大截面边缘纤维屈服作为计算准则.="" 这一准="" 63="" 则比较适用于冷弯薄壁型钢压弯构件,="" 因为这类构件的边缘纤维屈服荷载非常接近于构件的极限="" 荷载;该准则也用于格构式压弯构件绕虚轴弯曲的稳定计算.="" 参照式(3.17)="" ,给合压弯构件弯矩作用平面内的稳定概念,可以得到按边缘纤维屈服准则="" 导出的相关公式="" β="" mx="" m="" x="" p="" +="fy" (3.42)="" x="" a="" p="" w1x="" 1="" x="" pex="" 式中="">

为弯矩作用平面内轴心受压构件的整体稳定系数; W1x 为受压最大纤维的毛截面抵抗矩; β mx 为等效弯矩系数,参见表 3.1. 将式(3.42)写成设计公式,即 β mx M x P + ?f (3.43) x A P W x 1 x PEx 式中 f 为钢材屈服强度设计值. 2. 极限承载力准则 一般钢结构中的压弯构件当截面最大纤维刚开始屈服时尚有较大的强度储备, 即可以容许截 面塑性有一定发展,因此应该以 弹塑性稳定理论为基础,以失稳时的极限荷载为计算准则. 压弯构件的初偏心和初弯曲对构件的影响性质上相同,因此在制定规范时考虑构件存在 l 1000 的初弯曲(即初弯曲的矢高为构件长度 l 的 1/1000) ,考虑实测的残余应力分布,用数值方 法计算出近 200 条压弯构件的极限承载力曲线.将用数值方法得到的压弯构件极限承载力 Pu 与 用边缘纤维屈服准则导出的相关公式(3.42)中的轴心压力 P 比较后发现,对于短粗实腹杆,式 (3.42)偏于安全;而对细长实腹杆,式(3.42)偏于不安全.因此,规范借用了弹性压弯构件 边缘纤维屈服准则计算公式的形式, 同时考虑截面塑性发展和二阶弯矩, 最后提出了一近似相关 公式,即规范所采用的实腹式压弯构件弯矩作用平面内的稳定计算公式 β mx M x P + ? f (3.44) xA γ RP γ xW1x 1 0.8 PEx

式中 P ——所计算构件段范围内的轴向压力; M x ——所计算构件段范围内的最大弯矩; x ——弯矩作用平面内的轴心受压构件的稳定系数; W1x ——弯矩作用平面内较大受压纤维的毛截面抵抗矩; PEx——欧拉临界力; γ R — —抗力分项系数,对 Q235 钢,γ R = 1.087 ,对 Q345,Q390,Q420 钢,γ R = 1.111 ; β mx ——等效弯矩系数,参见表 3.1. 对于 T 型钢,双角钢 T 形等单轴对称截面压弯构件,当弯矩作用于对称轴平面且使较大翼 缘受压时,构件失稳时出现的塑性区除存在受压区屈服和受压,受拉区同时屈服两种情况外,还 可能在受拉区首先屈服而导致构件失去承载能力,因此除了按式(3.44)计算外,还应按下式计 算: 64 P A 式中 β mx M x γ P γ xW2 x 1 1.25 R PEx ? f (3.45) W2 x ——受拉侧最外纤维的毛截面抵抗矩; γ x ——与 W2 x 相应的截面塑性发展系数. 其余符号同式(3.44) ,上式第二项分母中的 1.25 也是经过与理论计算结果比较后引进的修 正系数. 3.2 压弯构件平面外失稳 如图 3.1(c)所示,当压弯构件没有设置侧向支撑时,在外荷载 P 尚未达到平面内弯曲失稳的 临界荷载 Pu 之前,就可能导致压弯构件发生空间的弯扭失稳,也称平面外弯扭屈曲.当构件长 细比较大时,有可能在弹性阶段失稳;在长细比较小等情况下也有可能在弹塑性阶段失稳. 对于外力作用和端部支

撑条件较简单的压弯构件,可以用平衡法求解弯扭屈曲荷载的精确 解;如果外力

作用或端部支撑条件较复杂,可以用能量法求解.在弹塑性阶段发生弯扭屈曲的压

弯构件,采用数值法可以获得较高的求解精度. 3.2.1 压弯构件的弹性弯扭失稳

压弯构件的弹性弯扭失稳 1. 平衡法求解单轴对称截面压弯构件的弹性弯扭屈

曲荷载 以两端简支单轴对称截面压弯构件(图 3.13)为例,说明平衡法求解弹性

弯扭屈曲荷载的过 程. 图 3.13 压弯构件弯扭变形及受力 65 分析中采用两个

坐标系,即截面的固定坐标系 oxyz 和移动坐标系 o ′ ξ (图 3.13) ,且 采用

如下假设: ? 构件为弹性体; ? 发生弯曲与扭转变形时,截面的形状不变; ?

弯曲与扭转变形微小; ? 构件是无缺陷的等截面直杆; ? 在弯矩作用平面内抗

弯刚度很大, 屈曲前平面内的弯曲变形对弯扭屈曲的影响可以忽略. 参考第二章

2.4 节中单轴对称截面轴心受压构件弹性弯扭失稳建立平衡微分方程的过程, 可

以分别得到绕ξ 轴和 轴 的弯矩平衡方程. EI xν ′′ + Pν + M x = 0 (3.46) EI y u ′′ + Pu + (M x + Py 0 ) = 0 (3.47) 由图 3.13a 所示受力条件和坐标系,如以压应

力为正值,则构件截面上任一点的正应力 P M y (3.48) , = x A Ix Wagner 效应系

数为 M P 2 2 K = ?A (, + , r )ρ 2 dA = ?A x 2 + ( y y 0 ) dA x ?A y x 2 + ( y y 0 ) dA

+ ?A , r x 2 + y 2 dA A Ix [ ] [ ] ( ) = 式中 : M P 2 I x + I y + Ay 0 x A Ix ( ) [? y(x A 2 + y 2 )dA 2 I x y 0 + ?A , r (x 2 + y 2 )dA = ρ i 0 2 β y M x + R 2 ] 2I x 是截面的

几何性质参数, β y 为不对称截面常数,对于单轴对称工形截面, β y 中前一项数

值常比 y 0 小得多,对图 3.13c 所示坐标系,剪心矩 y 0 是正值,则 β y 将是负

值. 外弯矩 M x 在纵轴 方向的分量为 i0 2 = (I x + Iy ) A+ y , 2 0 β y ? y (x = A 2 + y 2 )dA y 0 , R = ?A , r (x 2 + y 2 )dA . i 0 和 β y 都 M x sin ? M x = M

x u ′ 切力 Pu ′ 产生的扭矩从图 3.13c 知为 则在 方向总的非均匀扭矩 扭矩

平衡方程为 Pu ′ y 0 cos ? Py 0 u ′ 2 M = Pi 0 2 β y M x + R ′ + M x u ′ + Py 0 u ′ EI w ′′′ + Pi0 2 β y M x GI t + R ′ + (M x + Py 0 )u ′ = 0 2 ( ) (3.49) (3.50) ( ) 联立方

程(3.46)(3.47)和(3.50) , ,得到适合任何边界条件的压弯构件微分方程组 EI x ν IV

+ Pν ′′ = 0 (3.51) EI w IV + Pi0 2 β y M x GI t + R ′′ + (M x + Py 0 )u′′ = 0 2 ( EI y u

IV + Pu′′ + (M x + Py0 ) ′′ = 0 ) (3.52) (3.53) 由于忽略了屈曲前平面内弯曲变形对

弯扭屈曲的影响,因此方程(3.51)与后面两方程解耦, 只能用于描述平面内荷载—

挠度弹性曲线.后两个方程是耦联的,引入边界条件,可联立求解得 到构件的弹性

弯扭屈曲荷载 Pyw . 对两端简支的压弯构件,满足边界条件的变形函数为 π z π

z = c 2 sin u = c1 sin , l l 66 将它们代入方程(3.52)(3.53) , ,得 (M x + Py 0 )c 2 = 0

Py P c1 2 2 (M x + Py 0 )c1 + i0 Pw i0 P 2 β y M x c 2 = 0 ( ) [ ( )] (3.54) 式中: p y =

π 2 EI y l 2 , Pw = 2 1 π EI w + GI t R . 2 2 i0 l 由 c1 和 c 2 有非零解的条件为系

数行列式为零, 可以得到屈曲方程 (P y P ) i 02 Pw (i 02 P 2 β y M x ) (M x + Py 0 ) = 0 2 [ ] (3.55) 方程(3.55)中的 M x 以弯矩使形心以上的负方向受压时为正,受

拉时为负;而偏心矩 e y 符号与 y 轴正负一致,由图 3.13a 知 M x = Pe y ,代入

方程(3.55) ,则有 (P y P ) i02 Pw P (i02 + 2 β y e y ) ( y 0 e y ) P 2 = 0 2 [ ] (3.56) 2 解之得弹性弯扭屈曲荷载 Pyw = i 02 (Py + Pw ) + 2 β y e y Py [i (P 2 0 2 i02 + 2 β y e y ( y 0 e y ) y [ + Pw ) + 2 β y e y Py ] 2 4i02 Py Pw i 02 + 2 β y e y ( y 0 e y ) 2 ] [ ] (3.57) 相应的弯扭屈曲应力 , yw = Pyw A = π 2E λ 2 yw (3.58) 式中 λ yw 为

计算弯扭屈曲应力的换算长细化 λ yw = λ y 其中 w = 2 2 w 2 + i0 + 2β y e y 2w

2 2 w 2 + i0 + 2β y e y + 2w 2 i 2 + 2β y e y y 0 e y 0 w2 2 ( ) ( 2 ) 2 (3.59) A l2 对双

轴对称截面压弯构件,因 y 0 = 0, β y = 0, i02 = (I x + I y ) A ,则方程(3.55)为 λ 2y I

ω + GI t R . π 2E (P y P )(Pw P ) M x2 i02 = 0 (3.60) 解出弯扭屈曲荷载 1 Pyw =

Py + Pw 2 (P y + Pw ) 2 2 2 4 Py Pw M x l 0 ( ) (3.61) 对无对称轴截面压弯构件,开

始施加压力 P,构件就产生双向弯曲变形和扭转,因此属于极 值点失稳问题.对此

类问题用平衡法求解析解较困难,一般采用能量法[19]或数值法求解其极限 荷载.

【例题 3.1】 已知两端简支的单轴对称 T 形截面压弯构件的长度 例题 为 4m,

构件的两端作用有弯矩 M x = 10kN m ,截面尺寸如图 3.14 . 钢 材 , y = 23.5

kN cm 2 , E = 2.06 × 10 4 kN / cm 2 , G = 7.9 × 10 3 kN / cm 2 ,按理想弹塑性体计

算,不计残余应力.构 件在弯矩作用平面内的极限荷载 Pu = 735kN .求此压弯构

件的屈 曲荷载. 图 3.14 T 形截面压弯构件 67 [解]: 1) 计算截面的几何性质 截

面积 A=2 × 1 × 20=40cm 2 1 × 20(10 + 0.5) y0 = = 5.25cm 剪心矩 2 × 20 1 惯性

矩 I x = 1 × 20 × 5.25 2 + × 1 × 20 3 + 1 × 20 × 5.25 2 = 1769.2cm 4 12 1 3 I y = × 1

× 20 = 666.7cm 4 12 1 I k = 2 × × 20 × 13 = 13.33cm 4 , Iw = 0 3 Ix 对翼缘边缘抵

抗矩 W1x = = 307.07cm 3 5.25 + 0.5 I W2 x = x = 116cm 3 对腹板边缘抵抗矩

15.25 Ix + Iy 2 i02 = + y 0 = 88.46cm 2 A ? y (x A 2 7000 ( 5.25) = 1.98 + 5.25 =

7.23cm 2I x 2 × 1769.2 2) 计算 M x = 10kN m 时构件的弯扭屈曲荷载 Pyw β y =

? y (x A + y 2 )dA = t ? 4.75 y 3 dy + 2t ?0 ( 5.25)(x 2 + 5.25 2 )dx = 7000cm 5 15.25 10 2 + y 2 )dA y0 = Py = π 2 EI y l 2 = π 2 × 2.06 × 10 4 × 666.7 / 400 2 = 847.2kN Px = π 2 EI x / l 2 = π 2 × 2.06 × 10 4 × 1769.2 / 400 2 = 2248.2kN 3 1 2 Pw = 2 (π 2 EI w l w + GI k ) = GI k i02 = 7.9 × 10 × 13.33 = 1190.4kN 88.46 i0 由式(3.55)得

60.9 P 2 184206 P + 100463044 = 0 解出 (847.2 P )[88.46 × 1190.4 (88.46 P 2 ×

7.23 × 10 × 10 2 )] [10 × 10 2 + ( 5.25P )]2 = 0 Pyw = 713.86kN 3) 确定屈曲荷载

由于翼缘边缘纤维的压应力 713.86 10 × 10 2 1 + 0.234 × 713.86 2248.2 , 1 = +

=17.85+5.12= 22.97 kN cm 2 < ,="" y="23.5" kn="" cm="" 2="" 713.86="" 40="" 307.71="">

范文四：拉伸展开直径计算公式

各形状下的毛坯直径

的计算各形状下的毛坯直径D的计算d

555h 50D 647.3214

d1

35d250h 51D 98.1835

d

120l 50h 45D 183.303

d1

175d2137d3175h123h246D 2682033268.2033

l d1d2d3h1h2D

l d1d2h D

l d1d2D

l d1d2d3D

l d1d2h D

d1

98r 86.1D 349.1405

d1d2d3r

D

d1

计算公式一：d2h r D

d2

计算公式二：Ｈr D

d1d2d3h r D

l d1d2d3r D

d1

当r1≠r时,公式为d2h r

r1D

0d1

当r1=r时,公式为d2h r D

d1d2r D

d2

当r1=r时,公式为d4H r D

当r1≠r

时,公式d1d2d3d4h r r1D 0

h

16

或h

30s 100R 80D 104.9952D 138.5641

d2h D

0d D

d1d2D

l d1d2h1h2D

d h1h2D

d1d2h1h2D

l d1d2h D 0l d1d2D

d d1h D

d

或H D

d1d2h D

l d1d2h D

d1

22.3d280h127.8h29.2D 76.94836

设arc sin (x/R)的值为P,则有:

P

25b 56d 45h125h225R 10X 14r 45D 58.48077说明:

1.其中青色的部分,是我们根据实际情况要填写的部分,填好后起毛坯的直径计算结果会在对应的每套公式的最后格找到计算结果会在对应的每套公式的最后一格找到

2.请勿更改黄色和天蓝色部分中的内容.

范文五：【doc】关于压缩模量的计算公式

关于压缩模量的计算公式

土.釜偏髓.式

48l996年6月大坝观测与土工测试 ((3()

关于压缩模量的计算公式

(水利部天津勘测设计研兖院)

在SDS0179《土工试验规程?中压缩摸 量的公式是:

善…

1000

:一

i-~一e一

,

(2j一一一'

在SD128—81t士工试验规程》中压缩模 量的公式是:

一三?

::一cI)"一j】

在(;BJ123—88《土工试验方法标准?中压 缩摸晕的公式是:

一一?

一

F?)

以上几个公式中朽符号的含义是一样的. 即:

某压力范围内的压缩模量【kPa); 一

某压力范围内舶体积压缩系数 f

尉图

l^n'l-J

压缩模祭定义示图

F示图及演绎

如按匕I上(3)式则有:

E…:0二I,P:_一一(7)n- ?

一lIl,_

:i[0.^l《8)

一?^.

(kPa):

"——压缩系数(kPa.): .试样的初始孔隙比:

,,一一

各级压力下试样固结稳定后的孔隙比:

s——单位沉降量(I11rt1./'E1]);

,).一某级压力值(kPaj .

然上公式':,I之问列压缩模量的由【8)式可

定义是有矛盾的为什么会有矛盾呢?请看匕I

P,_

…

^

^

,'.,,h.一^+h

HL

h一h.

h

:—

,

:?

一J"一..J'

,._】

得:

^P—

一

l0j

埔

第

卷

9

.

第

橡树^关于压缩模量的计算公式49

其中EI…Ahl,

_..…:墨堂=

lipc,

如按以上(2)式则有: 陷量的,但却不符合压缩模量原来既定的定义.

AP,一这里再看一下弹性模量的情况.通常是定

(11)义"弹性模量是应力与应变之比",即:

I

—

+=cl2)

一

+等一

一?:五一一j一

?尸...+^

-

?P…1一^,(13)

一

拿(14)…+1

…

^.

由(13)式可得:

Ah…+一)

从上演绎中看(7)式显然是符合原来既 定的"压缩模量是压力增量与应变增量之比"的 定义的.而从【14)式看则只能得到"压缩模量 是压力增量与相应应变之比"这样的定义. 但从应用的角度看.常常是在某土层发生 一

个应力增量(附加应力)后要求其沉陷量.若 按(i0)式计算沉陷量.则式中的^.不能从i状 态及+l状态中直接得到,只能按(?)式去求 得.而从(11)式看^.的求得要追溯到?,.+. 发生前的部分或全部应力历史中发生的与 AP…一或Ap,相应的E和Ah,这只能在 压缩试验的应力历史中可以找到依据.若用 (15)式求沉陷量,其中的^却只是应变增量发 生前土层的厚度,这是很容易测得的. 所以若(7)式为依据来定义压缩模量就 应用t1o)式来计算沉陷量.这将给沉陷量计算 带来很多的不便,但这是符合原来既定的压缩 模量的定义的若以(14)式为依据来定义压缩

模量就应用(15)式来计算沉陷量.这可使沉陷

量的计算变得十分简捷,在许多土力学书中都

是使用压缩模量的这个定义指标来计算土层沉

F=二—L

'.Ah.+l

若使?尸…】==立,,. 限度内有:

一.l-=Ahl,.= 成为:

E一?…i)一A—P ("1)

,一__,—一

??P

?Ah…+

n

--?==

AP.

(16)

则在弹性

一

Ah,则(I6)式就

AP

:—

A

l,J

P

—

,~

一

i+i(17)

??^…一

T

?一??Ah?

一一—】_一…—L—

hh.

(18)

从(18)式看.若定义"弹性模量是应力增量与 应变增量之比"也是与通常定义的弹性模量相 等同的,并都等于应力应变曲线上直线段斜率 的倒数乘原始高度,所以在弹性范围内弹性模 量是常量.事实上弹性模量虽然通常是l6) 式来定义的,但在应用时却都是按18)式的定 义来使用的

如果仿照【l11)式定义"弹性模量是应力增 量与应变之比",则:

一=

畿?也一叫l.二

—^I一

此(19)式中?尸._./ih一._.为应力应变曲线斜 率的倒数,是常数,而^为变数,所以此时弹 性模量在弹性限度内也是变化的.当然这种定 义会使问题复杂化,因而是不可取的.但在土 的压缩变形中,若按(14)式来定义压缩模量却 可以使土体沉降量的计算简捷,因而是可取的. 所以笔者建议应重新定义"土的压缩模量是应 力增量与相应应变之比,这样会便于应用

转载请注明出处范文大全网 » 拉伸常用计算公式