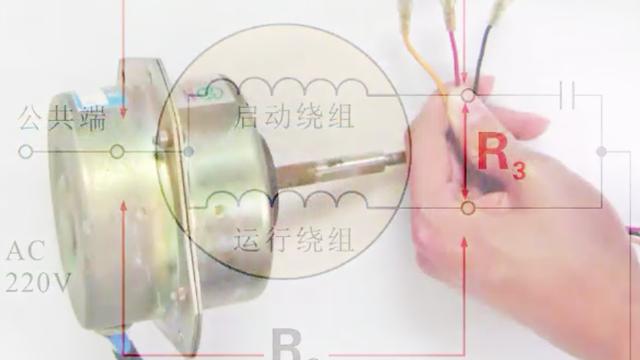
范文一:判断三相电机绕组电路
判断三相电机绕组及其首尾的方法很多,如用发光二极管来判断,简便易行,安全迅速。判断连接电路如图1所示。
(1)同相绕组判断:将两节电池串接,再按极性和发光二极管的一极相接,另一极和电机的任一抽头相接,其余抽头分别和电池的另极触碰,发光二极管亮者为同相绕组。
(2)绕组首尾判断:先把电机任意两相绕组的一端相接,另两端和发光二极管的两极相接,剩下一相绕组的一端和电池的负极相接,另端和电池的另极触碰。接 通瞬间,若发光二极管亮,则电池正极、发光二极管的负极和发光二极管正极所接绕组的另端,同时绕组的首或尾,一次判清。若不亮,可改换电池的电极或绕组接 头再试,若怎么改接发光二极管都不亮,应检查电池、发光二极管和各个接头到亮为止。
图1:一款电机绕组判断电路
范文二:三相交流电机的绕组讲义
第一讲 三相交流电机的绕组
一、三相交流电机及其绕组 1.三相交流电机的种类和结构
三相异步电机 鼠笼式 绕线式 三相同步电机 凸极式 隐极式
(定子均为三相交流绕组)
2.三相交流电机的工作原理 交流励磁磁场和直流励磁磁场 同步电动机的起动 3.三相交流绕组
(一)三相交流绕组的作用
三相交流绕组的作用
(二)三相交流绕组的要求
电磁方面
① 在绕组中通过三相对称电流时,气隙中有旋转磁场; ② 气隙中有旋转磁场时,绕组中感应产生对称的三相电势; ③ 交流绕组的电势和磁势应为按正弦规律变化的时间波和空间波,
即其谐波分量尽可能小;
结构方面
④ 三相交流绕组在空间作对称分布(即其轴线互差2π/3 电角度); ⑤ 各相绕组的匝数应相相同。
(三)三相交流绕组的的基本概念
(1)极对数
a )一对极的三相交流绕组 b ) 一对极磁场的磁力线 c )二对极的三相交流绕组 d ) 二对极磁场的磁力线
(2)电角度
每对磁极对应360°电角度 ; 整个圆周上,360°机械角度。
一对极的 电角度为 360° 二对极的 电角度为 720°
p 对磁极的 电角度 = 机械角度 × p (3-1)
二对极的 电角度为 720°
p 对磁极的 电角度 = 机械角度 × p
↑ 12槽 ↑
二对极的 电角度为 720°
p 对磁极的 电角度 = 机械角度 × p
↑ 24槽 ↑ (3)相带
每极每相交流绕组在电枢圆周上连续占据的电角度称相带。
三相交流绕组通常为60° 相带。
(4)每极每相槽数
为使三相绕组感应电势对称,每相在每极下应占有相等的槽数, 该槽数称每极每相槽数,用q 表示。
↑ q = 2 ↑
(3-2)
式中,m - 相数;
Z - 电枢圆周总槽数。
(5)整数槽与分数槽
(6)节距
一个线圈的两个线圈边之间沿电枢气隙圆周上的跨距称为节距, 用y 1表示。
节距可用长度单位表示,也可用槽数表示。
● 一般三相60相带双层绕组,取y 1≈(5/6)τ,以削弱5、7次谐波。
(7)单层绕组
一个线圈有二个线圈边。
单层绕组在每槽内只安放一个线圈边。
● 单层绕组排列与串、并联
串联
(8)双层绕组
并联
习惯上,线圈的编号同其上层边所在的槽号。
(9)槽间角、极距
相邻两槽之间所间隔的电角度称为槽间角,以α1表示。
(3-3)
(10)三相绕组的排列
① 每一相绕组的有效边都 是由放置在相同槽号 中的导体组成; ② 导体中电流规定的正方
向不变;
③ 电磁作用相同。所不同 的是绕组端部的连接 方式。
(a)排列次序;(b)链式;(c)同心式;(d)交叉式
(11)三相绕组
⑴ 一对极、集中、整距
槽数:Z = 6; 极对数:p = 1 极距:τ = Z /(2p ) = 6/2 = 3;
每极每相槽数:q = Z /(2pm ) = 6/(2×3) = 1
节距:y 1 = Z /(2p ) ± ε = 6/2±0 = 3 (整距,ε = 0,y 1 = τ) A 相线圈:1—4 B 相线圈:3—6 C 相线圈:5—2
⑵ 一对极、分布、整距 链式
槽数:Z = 12; 极对数:p = 1 极距:τ = Z /(2p ) = 12/2 = 6;
每极每相槽数:q = Z /(2pm ) = 12/(2×3) = 2
节距:y 1 = Z /(2p ) ± ε = 12/2±0 = 6 (整距,ε = 0,y 1 = τ) A 相线圈(2个):1—7、2—8; A 相线圈组(1个):1—7—2—8; B 相线圈(2个):5—11、6—12; B 相线圈组(1个):5—11—6—12; C 相线圈(2个):9—3、10—4; C 相线圈组(2个):9—3—10—4;
同心式
槽数:Z = 12; 极对数:p = 1 极距:τ = Z /(2p ) = 12/2 = 6;
每极每相槽数:q = Z /(2pm ) = 12/(2×3) = 2
A 相线圈(2个):1—8、2—7; A 相线圈组(1个):1—8—2—7; B 相线圈(2个):5—12、6—11; B 相线圈组(1个):5—12—6—11; C 相线圈(2个):9—4、10—3; C 相线圈组(2个):9—4—10—3;
交叉式
槽数:Z = 12; 极对数:p = 1 极距:τ = Z /(2p ) = 12/2 = 6;
每极每相槽数:q = Z /(2pm ) = 12/(2×3) = 2
A 相线圈(2个):2—7、8—1; A 相线圈组(1个):2—7—1—8; B 相线圈(2个):6—11、12—5; B 相线圈组(1个):6—11—5—12; C 相线圈(2个):4—9、10—3; C 相线圈组(1个):9—4—3—10;
⑶ 四、二对极、分布、整距
槽数:Z = 36; 极对数:p = 2 极距:τ = Z /(2p ) = 36/4 = 9(槽); 每极每相槽数:q = Z /(2pm ) = 36/(4×3) = 3
A 相线圈(6个):1—10、2—11、3—12、19—28、20—29、21—30; A 相线圈组(2个):1—10—2—11—3—12;19—28—20—29—21—30; B 相线圈(6个):7—16、8—17、9—18;25—34、26—35、27—36; B 相线圈组(2个):7—16—8—17—9—18;25—34—26—35—27—36; C 相线圈(6个):13—22、14—23、15—24;31—4、32—5、33—6; C 相线圈组(2个):13—22—14—23—15—24;31—4—32—5—33—6;
槽间角:α1 = 2p π/ Z = 4×180°/36=20°;
基波分布系数:k q1 =[Sin(q α1/2) ]/[q Sin(α1/2) ]
=[Sin(3×20°/2) ]/[3×Sin(20°/2) ]= 0.96
基波绕系数:k N1 = kq1 ky1= 0.96×1= 0.96
三次谐波分布系数:k q3 =[Sin(q να1/2) ]/[q Sin(να1/2) ]
=[Sin(3×3×20°/2) ]/[3×Sin(3×20°/2) ]= 0.67
三次谐波绕系数:k N3 = kq3 ky3= 0.67×1= 0.67
五次谐波分布系数:k q5 =[Sin(q να1/2) ]/[q Sin(να1/2) ]
=[Sin(3×5×20°/2) ]/[3×Sin(5×20°/2) ]= 0.22
五次谐波绕系数:k N5 = kq5 ky5= 0.22×1= 0.22
⑷ 二对极、分布、短距 (不完整)
(比较)
节距:y 1 = 7(槽); (A 相完整,B 、C 不完整)
槽数:Z = 36; 极对数:p = 2 极距:τ = Z /(2p ) = 36/4 = 9(槽); 每极每相槽数:q = Z /(2pm ) = 36/(4×3) = 3
A 相线圈(12个):1—8、2—9、3—10、 19—12、18—11、17—10、 19—26、20—27、21—28、1—30、36—29、35—28。 A 相线圈组(4个):1—8—2—9—3—10; 19—12—18—11—17—10; 19—26—20—27—21—28;1—30—36—29—35—28。 (A 、B 相完整, C 不完整)
B 相线圈(12个):7—14、8—15、9—16、 25—18、24—17、23—16; 25—32、26—33、27—34、 7—36、 6—35、 5—34。 B 相线圈组(4个):7—14—8—15—9—16;25—18—24—17—23—16; 25—32—26—33—27—34、 7—36—6—35—5—34。
(完整)
C 相线圈(12个):13—20、14—21、15—22、31—24、30—23、29—22、 31—2、 32—3、 33—4、 13—6、 12—5、 11—4。 C 相线圈组(4个):13—20—14—21—15—22;31—24—30—23—29—22;
基波短距系数:k y1 = Sin[πy 1/(2τ) ]= Sin[180°×7/(2×9) ]= 0.94 基波绕系数:k N1 = kq1 ky1= 0.96×0.94 = 0.90
三次谐波短距系数:k y3 = Sin[νπy 1/(2τ) ]= Sin[3×180°×7/(2×9) ]= -0.5 三次谐波绕系数:k N3 = kq3 ky3= 0.67×(-0.5) = -0.335
五次谐波短距系数:k y5 = Sin[νπy 1/(2τ) ]= Sin[5×180°×7/(2×9) ]= -0.17 五次谐波绕系数:k N5 = kq5 ky5= 0.22×(-0.17)= -0.04
⑸ 二对极、分布、短距(又例)
2p =4,Z =48,y 1=9,a = 2,每极每相槽数q = Z /(2pm ) = 48/(4×3) = 4, 极距:τ = Z /(2p ) = 48/4 = 12(槽);
A 相线圈(16个):1—10、2—11、3—12、4—13、 25—16、24—15、23—14、22—13、 25—34、26—35、27—36、28—37、 1—40、48—39、47—38、46—37。 A 相线圈组(4个):1—10—2—11—3—12—4—13; 25—16—24—15—23—14—22—13; 25—34—26—35—27—36—28—37;
A 相支路数(2个):1—10—2—11—3—12—4—13—25—16—24—15—23—14—22—13;
25—34—26—35—27—36—28—37—1—40—48—39—47—38—46—37;
B 相线圈(16个):9—18、10—19、11—20、12—21、 33—24、32—23、31—22、30—21、 33—42、34—43、35—44、36—44 9—48、8—47、7—46、6—45。 B 相线圈组(4个):9—18—10—19—11—20—12—21; 33—24—32—23—31—22—30—21、 33—42—34—43—35—44—36—44
B 相支路数(2个):9—18—10—19—11—20—12—21—33—24—32—23—31—22—30—21;
33—42—34—43—35—44—36—44—9—48—8—47—7—46—6—45
。
C 相线圈(16个):17—26、18—27、19—28、20—29、 41—32、40—31、39—30、38—29、 41—2、42—3、43—4、44—5、 17—8、16—7、15—6、14—5。 C 相线圈组(4个):17—26—18—27—19—28—20—29、 41—32—40—31—39—30—38—29、 41—2—42—3—43—4—44—5、
C 相芝路数(2个):17—26—18—27—19—28—20—29—41—32—40—31—39—30—38—29、 41—2—42—3—43—4—44—5—17—8—16—7—15—6—14—5。
二、三相交流绕组的磁势
↓ ↓
* 一相集中整距绕组的磁势
单个整距线圈磁势的波形
将此矩形波用傅氏级数进行分解,得基波和各次谐波的幅值为
F c ν=
1
π
2
∫
νπ
2π0
f c (x ) cos νxdx I c N
c
=
sin
νπ
2
式中,v =1,3,5,7, ...。当v =1时,F c 1为基波磁势的幅值;此外,值。
若把空间坐标
F c ν
为v 次谐波磁势的幅
x (机械弧度)也改用对基波的电角度α表示,则由一个整距线圈构成相绕
f c (t , α) =
22
111??
I c N c ?cos α?cos 3α+cos 5α?cos 7α+....... ?sin ωt (7-1) π357??
其中,基波磁势为
f c 1(t , α) =
其最大值为
F c 1=
22
π
I c N c cos αsin ωt (7-2)
2π
I c N c =0. 9I c N c (7-3)
v 次谐波磁势为
f c ν(t , α) =
其最大值为
1?22νπ?I N sin c c
2ν??π?
??cos να?sin ωt (7-4) ??
F c ν
?1?22
?I c N c ?=?? (7-5) ν?π?
可见,分解后的磁势基波和各次谐波既是时间角ωt 的函数,又是空间角α的函数。
* 线圈的分布和短距对磁势的影响
实际交流电机的交流绕组为了充分利用铁芯通常采用沿定子圆周分布排列的。本节将讨论绕组的分布和短距对绕组磁势的影响。
一、线圈分布的影响
在交流电机中,无论单层绕组或双层绕组,每相绕组都是由若干个线圈串联或并联组成。就产生磁势的效应而言,不论具体的线圈结构如何,都可等效地认为每个线圈组由若干个节距相等、匝数相同、依次沿定子圆周错开一个角度(通常为一个槽距角)的线圈串联而成。
图7-5所示为三个线圈串联的线圈组。各线圈沿定子,圆周依次位移一个槽,对基波来说为α1电角度,如图7-5(a)所示。则各线圈磁势的v 次谐波依次在空间上位移v α1电角度。
r
用空间矢量表示时,各线圈的v 次谐波磁势矢量F c ν依次有一空间相位差v α1,如图7-5(b)
r
所示。于是用矢量相加可求得该线圈组磁势的v 次波幅值F q ν如图
7-5 (c)所示。
图7-5 由三个线圈串联的线圈组磁势的ν次波
(a)多线圈的空间位置;(b) 多线圈的ν次波磁势矢量;(c) 线圈组的ν次波磁势矢量
显然,F < q="" f="" 。这一减小可用一个分布系数k="">
k ν
q q
=
F ν q ν
q c c
q
为交流绕组磁势空间v 次波的分布系数。即
F ν=q F νk ν (7-6)
式中,k q ν可由图7-5(c)中的矢量的几何关系求得
k ν=
q
sin
q ν1
q sin
ν1
2
(7-7)
当v =1时,
k
即为基波的分布系数。 当q 相当多时,
sin
q 1
2 (7-8)
=q 1
q sin 1
2
k ν=
q
sin
νπ
6
6
v =1, k q 1 = 3/π = 0.955 v =3, k q 3 = 2/π = 0.637 v =5, k q 5 = 3/(5π) = 0.191
......
以此类推,可见当v 不太大时,k q ν随v 的次数增加而明显衰减。因此说,利用绕组的分布排列可有效地削弱谐波磁势,改善交流绕组磁势波形,使之接近正弦波。
二、线圈短距的影响
如前所述,y 1为线圈的两线圈边之间的节距,τ为极距,当y 1<τ时称短距。通常在>
定义
β=
称为相对节距。
短距线圈缩短的距离为
y
τ
1
τ-y 1,缩短距离的相对值为
τ?τ
y
1
=1?β=ε或
π?y
1
=1?β=ε 。 比较两个整距和短距线圈的磁势,见图7-6所示
图7-6 两个线圈的磁势
(a) 两个整距线圈的磁势;(b) 两个短距线圈的磁势
r r
图7―6 (a) 中两个整距线圈11 和22的磁势分别为F c 1和F c 2,两矢量大小相等、方向
r
’’
相同,其合成磁势为F y ,即F y =2F c 1=2F c 2。图7-6( b)中两个短距线圈11 和22产生的磁
r r
’’
势可等效为由两个整距线圈12和12所各自产生的磁势F c 1和F c 2。这两个矢量不同向,其合
’
’
成磁势为y ε。显然,F y ε<F y 。同样,这一减小的折扣可用一个短距系数k y ν来体现。
定义:
k ν
y
=
F ε y y
为交流绕组磁势空间v 次波的短距系数。
由图7-6 (b)的几何关系可得
F
则
y ε
=2F c 1COS
νεπ
2
F ε=COS νεπ
k ν=
2F
y
y
y
=sin
νπ
y
1
2τ
(7-9)
式中 v =1,3,5,7 ...。
当v =1时,
k y 1=COS
επ
2
=sin
π
y
1
2τ
(7-10)
称为基波短距系数。
利用绕组的短距可以有效地削弱谐波磁势,使之接近正弦波。通常取
y 1≈5τ/ 6
分布系数和短距系数的乘积为绕组数系数,即
k N ν= k q ν·k y ν (7-11) 式中,k N ν
── 交流绕组磁势空间v 次谐波的绕组系数。
当v =1时,
称为基波绕组系数。
* 单相绕组的磁势
一、单相脉振磁势
对于p 对极的整数槽绕组,设每相绕组总匝数为N φ,则每相每对极串联匝数为N φ绕组的导体内电流有效值为I c ,根据前面分析的结果可得每相每极基波磁势为
/p 。
f φ(t , α)=
1
22
π
I
N
C
φ
p
k
N 1
COS α?sin ωt
每相电流有效值为I ,每相有a 条支路,每相每条支路的串联匝数为N ,则I c =I /a , N φ=
a N 。于是,每相每极基波磁势为
2()t , α=f φ1
πIN p
k
N 1
COS α?sin ωt
(7-13)
每相每极基波磁势的最大值为
F φf
1
=
2
2IN πp
k
(
N 1
=0. 9
IN
p
k
N 1
(安/极) (7-14)
每相每极v 次谐波磁势为
φν
(t , α)=
2
2IN πνp
k
N ν
sin
νπ
2
COS να?sin ωt
(7-15)
每相每极v 次谐波磁势的最大值为
F φν
=
2
IN πνp
k
N ν
=0. 9
IN νp
k
N ν
=
1
ν
N νN 1
F φ
1
(安/极)
(7-16)
综合以上分析可得出如下结论:
一相交流绕组产生的磁势为一个脉振磁势。该磁势脉振频率与绕组内正弦波电流频率相同,为f 1。该磁势沿气隙圆周近似地按梯形分布,它可按空间角分解为基波和一系列谐波。基波和每个谐波空间位置不变,而波幅以同一频率f 1按正弦规律交变。当绕组内电流为非正弦波时,可按时间角将它分解为基波和一系列谐波。这些波各自对应有以空间角分解的基波和各次谐波的磁势。
为了改善电机性能,应设法削弱磁势中的谐波,常采用短矩和分布绕组来实现。 二、脉振的相绕组磁势分解为两个旋转磁势
对于脉振的基波磁势可分为两个幅值相等、速度相同但方向相反的旋转磁势:
f φ(t , α)=F φCOS α?sin ωt
1
1
1
=F φ1[sin (ωt ?α)+sin (ωt +α)]=2
f
+
+
f
?
式中,
f +=
1
F φ1 sin (ωt -α) 2
1
F φ1 sin (ωt +α) 2
是一个正转的旋转磁势,即其幅值不变,其幅值的位置随时间不断沿α增大的方向移动;而
f ?=
是一个反转的旋转磁势,即其幅值位置随时间不断沿α减小的方向移动。
旋转磁势f +、f ?的幅值均为
F φ
2
1
;其转速由绕组内电流角频率ω及绕组的极对数p 决定,
为
60f
(r/min)。 p
正、反转的旋转磁势f +、f -的物理意义可解释为:在ωt –α =
π
2
情况下,f + =
1
F φ1为2
其幅值;在ωt + α =
π
2
情况下,f - =
1
F φ1为其幅值。也就是说,对应不同的时刻t ,这二2
个旋转磁势的幅值位置(α)也不同。正转的旋转磁势f + 随时间推移沿顺相序方向移动,故谓正转;反转的旋转磁势f - 随时间推移沿逆相序方向移动,故谓反转。表7-1、表7-2和图7-7给出正、反转的旋转磁势f +、f -在几个时刻对应的幅值位置。
表7-1 正转的旋转磁势f
的几个幅值位置
表7-2 反转的旋转磁势f –的几个幅值位置
(a ) (b ) (c )
(d ) (e )
图7-7 正、反转旋转磁势f + 、f –的几个幅值位置
(a )ωt = 0时;(b )ωt =
π
2
时;(c )ωt = π时;(d )ωt =
3
π时;(e )ωt = 2π时; 2
同理,对于每次谐波脉振磁势也可以各自分解为两个幅值相等、速度相同但方向相反的旋转磁势:
f
φν
(t , α)=(F φνsin νπ
2
) COS να?sin ωt
1=2
F φνsin
νπ
2
[sin (ωt ?να)+sin (ωt +να)]
第四节 三相交流绕组的合成磁势
一. 基波磁势
设三相交流绕组内通过的三相电流如图7-8所示,分别为
i i
A
==
222
I I I
C
sin ωt sin(ωt ?120sin(ωt ?
240
o
B C
) )
i C =
o
C
图7-8 三相电流
三相交流绕组在空间分布互差120°电角度,则三相交流绕组的其波磁势分别为
f f f
A 1
===
22
2IN πp
k k k
N 1
sin ωt cos α
B 1
IN πp 2IN πp
sin ωt ?120N 1
sin ωt ?N 1
(
o
)cos (α)cos (α
)]
??
?120?
o
)
o
2
C 1
(
240
o
240
)
(7-17)
将各相脉振磁势分解为二个旋转磁势
f f f
A 1
=
B 1
C 1
1
21=21=2
F F F
φ1
[sin (ω
t ?αt ?αt ?α
)+)+)+
sin sin sin
(ω
t +α
φ1
φ1
[sin [sin
(ω(ω
(ωt +α(ωt +α
240120
o
o
)])]
(7-18)
三相交流绕组合成磁势的基波为 f 1(t , α) = f A 1+ f B 1+ f C 1 =
3 2
F φ1 sin (ωt -α)
=F 1sin (ωt -α) (7-19) 这是一个波幅值恒定圆形的旋转磁势,如图7-9所示。 式中
3?22IN 3
? F 1 = F φ1 = ?
2?2πp ?
=1. 35
?32IN
k N 1??=π?p
?
k
N 1
IN p
k (安/极) (7-20)
N 1
为三相交流绕组合成磁势基波的最大值。其值为每相脉振磁势波波幅的
3
倍。其转向为正相序,2
即幅值位置从A 相绕组轴线(图7-9中的A 轴)转向相位滞后120的B 相绕组轴线(图7-9中的B 轴),再转向C 相绕组轴线(图7-9中的C 轴)。合成磁势波的转速为
n 1=
60f
(r /min ) (7-21) p
称同步速。
由图7-9显见:当某相绕组内的电流达到最大值时,三相合成磁势基波幅值位置恰在该相绕组的轴线上。
二、谐波磁势
三相交流绕组v 次谐波磁势
νπ?
?F φνsin ?sin ωt cos ναf ν(t , α)=?
2??
A
νπ?
ν(α?120)] ?F φνsin ?sin (ωt ?120)cos [f ν(t , α)=?
2??
o
o
B
νπ?o o ?
()()[(t , α=sin sin ωt ?cos να???f C ν240240)]F φν
?
2?
各相脉振磁势分解为二个旋转磁势
f A ν= f B ν=
1νπF φν sin[sin(ωt -v α)+sin(ωt +v α)] 221νπF φνsin 22
?sin ωt ?
120?
??+sin ωt ?120
(
o
(
?να
o
+ν
+να
120
?ν120
?
o
)
o o
)
o
?? ???? ??
1νπ
f C ν=F φνsin
22
对于三次谐波
?sin ωt ?
240?
??+sin ωt ?240
(
o
(
?να
o
+ν
+να
240
ν240
)
)
1
[ sin(ωt- 3α)+ sin(ωt+3α)] 2F φ31
fB3(t,α)=-F φ3[ sin(ωt-3α-1200)+ sin(ωt+3α-1200)]
21
fC3(t,α)=-F φ3[ sin(ωt-3α-2400)+ sin(ωt+3α-2400)]
2
fA3(t,α)=-
三相交流绕组合成磁势的三次谐波为
f 3(t,α)= fA3 + fB3 + fC3 = 0
由此可分得出如下结论:三相交流绕组的三次及三的整数倍次谐波合成磁势均为零。
对于五次谐波
1
[sin(ωt-5α)+ sin(ωt+5α)] 2F φ51
fB5(t,α)=F φ5[sin(ωt-5α+1200)+ sin(ωt+5α)]
21
fC5(t,α)=F φ5[sin(ωt-5α+2400)+ sin(ωt+5α)]
2
fA5(t,α)=
三相交流绕组合成磁势的五次谐势为
f 5(t,α)=fA5 +fB5 +fC5 =
3
sin(ωt+5α) 2F φ5
= F5 sin(ωt+5α) (7-22)
其最大值为
F5 =
332IN
?= k F φ5N 5
2π5p
IN
(安/极) (7-23) k N 5
5p
=1.35
由此可见,三相交流绕组的五次谐波合成磁势是一个波幅恒定、逆基波磁势转向的旋转磁势,即与基波转向相反,其转速为
n 5=
5
1
=
60f
(r/min) (7-24) 5p
旋转波的波长为基波的
对于七次谐波
1
,全圆周共有5对极。 5
1
[ sin(ωt-7α)+sin(ωt+7α)] F φ7
210
fB7(t,α)=-F φ7[ sin(ωt-7α)+ sin(ωt+7α-240)]
21
fC7(t,α)=-F φ7[ sin(ωt-7α)+ sin(ωt+7α-1200)]
2
fA7(t,α)=-
三相交流绕组合成磁势的七次谐势为
f7(t, α)= fA7+ fB7+ fC7 =-3
sin(ωt-7α) 2F φ7
= - F 7 sin(ωt- 7α ) (7-25)
其最大值为 F 7 =
3IN IN
?1. 35== k k F φ7N 7N 7
2π7p 7p
1N 7(安/极) (7-26)
F 71N 1
=
可见,三相交流绕组的七次谐波合成磁势是一个波幅恒定的正向旋转磁势,即转向与基波相同,
其转速为
n 7=
7
1
=
60f
(r /min ) (7-27) 7p
(a) (b)
(c) (d)
(e) (f)
图7-9 三相绕组基波合成磁势
(a) ωt = 0时,i A = 0;(b) ωt = 90时,i A = I m ;(c) ωt = 150时;(d) ωt = 210时,i B = I m ;
000
(e) ωt = 270时;(f) ωt = 330时,i C = I m
00
综上所述,对称三相交流绕组合成磁势中包含有v = 6k±1(k=1、2、3、......) 次谐波。一般地说,当对称m 相电流通过对称m 相绕组时,绕组合成磁势中包含着下列次数的高次谐波:
v =2mk ±1 (7-28)
式中k =1、2、3、...;当取加号时,谐波磁势转向与基波的转向相同。
谐波磁势(或相应的谐波磁场〕的存在,在交流电机中引起附加损耗、振动和噪声等不良影响,对异步电动机还将引起附加转矩,使电动机的起动性能变坏。因此,在设计电机时应尽量削弱磁动势中的高次谐波,采用短距和分布绕组是达到这个目的的很重要方法。
例7-1 有一个三相单层同心式绕组,2p =2,Z =24,其一相的端部联接画如图7-10所示,属同一相带的线圈出槽后端接线分向二侧弯走,若每个线圈的匝数相同,其基波绕组系数是多少?
图7-10
解 把该绕组看作是等效的整距分布绕组: 每极每相槽数 q =4 , 短距系数 k y 1=1 则基波绕组系数即是分布系数 k N 1
sin 30o sin 30o
=k q 1===0. 958 o o
3030
4sin q sin q 4
例7-2 一台50000 kW的2极三相汽轮发电机,50Hz ,U N = 10. 5 kV,Y联接,cos ?N
= 0.85,定子为双层叠绕组,Z = 72槽,每个线圈一匝,y 1=2τ/3,a = 2。试求当定子电流为额定值时,三相合成磁势的基波、3、5、7次谐波的幅值和转速,并说明转向。
解 I =I N =
P N U N COS ?N
=
500003×10. 5×0. 85
= 3234.46 A
τ=
Z 72
==36槽 , 2p 2Z 72
==12 2pm 2×3
2pqN c 2×12×1
==12匝 a 2
q =
N =y 1=
5τ5×36==30 66
p ×360o 1×360o
α1===5o ,
72Z
k N 1
q α112×5o sin sin y 130o o 22=sin(90×) ×=sin 90××=0. 9227 o
36τ5q sin 112×sin
22
k N 3
q να112×3×5o
sin sin y 1?30???o o =?0. 4514 =sin ?3×90×?×=sin ?3×90×?×o
τ?36?3×5??q sin 112×sin 22
同理求得
k N 5=0. 0498, k N 7=0. 3007 F 1=1. 35×
F 3=0 F 5=1. 35×
NI 12×3234. 46
×k N 1=1. 35××0. 9227=48347. 9 安匝/极 p 1
NI 12×3234. 46×k N 5=1. 35××0. 0498=52. 4安匝/极 5p 5NI 12×3234. 46×k N 7=1. 35××0. 3007=2250. 9安匝/极 7p 7
F 7=1. 35×
n 1=
60f 60×50==3000 r/min(转向:顺相序正转) p 1
三相合成的三次谐波磁势为零,所以也不存在转速n 3
n 5=
n 13000==600 r/min(转向:逆相序反转) 55n 13000==428. 6 r/min(转向:顺相序正转) 77
n 5=
例7-3 三相异步电动机,定子绕组为双层短距绕组,Y 联接,槽数Z = 48,极数2p = 4,线圈节距y 1=10,线圈匝数N c =22匝,每相并联支路数a =4,通入电流I =37A ,频率
f =50Hz 。试求:
(1)一相绕组磁势的基波和3次谐波的幅值,写出各项基波磁势的表达式;
(2)三相绕组合成磁势的基波和3、5、7次谐波的幅值,转速及转向; (3)写出三相合成磁势基波的表达式。
解 (1)一相绕组的磁势为脉动磁势,各次谐波磁势的幅值为
F φv =0. 9
每极每相槽数
k N νN 1k N
I =0. 9×?N νI p νv p
Z 48p ×360o 2×360o
q ===4, 槽距角 α===15o
2pm 4×3Z 48
极距
τZ p =
2p =484
=12 , 基波分布系数
sin q α4×15o k q 1=
2sin
=2=0. 958 q sin 15o
24sin
2
基波短距系数
k y 1
y 1=sin
τ?90o =sin
10
12
×90o =0. 966 p
基波绕组系数
k N 1=k q 1k y 1=0. 958×0. 966=0. 925
每相串联匝数列
N =
2pqN c a =4×4×22
4
=88 匝 基波磁势幅值
F 0. 9k w 1N 0. 9×0. 925φ1=
p I =×88×37
2
=1355. 3(A ) 3次谐波分布系数
sin
q 3αsin 4×3×15o
k q 3
===0q sin 24sin
3×15o
. 65 2
3次谐波短节距系数
k y 1
10
y 3=sin
τ×3×90o =sin
p
12
×270o =?0. 707 3次谐波绕组系数
k wN 3=k q 3k y 3=0. 65×(?0. 707) =?0. 46
3次谐波磁势幅值
F 0. 9k N 5N φ3=
3p I =0. 9×(?0. 46) ×88×37
3×2
=?224. 66各相的基波磁势表达式为
f A =1355. 3sin x sin ωt
f B =1355. 3sin(x ?120o ) sin(ωt ?120o ) f C =1355. 3sin(x +120o ) sin(ωt +120o )
(2)求三相合成磁势幅值、转速及转向 1)基波磁势幅值为 F 1=32F 3
φ1=2
×1355. 3=2033, 转速
A
n 1=
60f 60×50
==1500 r/min (转向:正向旋转) p 2
2)3次谐波合成磁势为零;
3)5次谐波磁势幅值为
F 5=
转速
3
×15. 53=23. 3 A , 2
60f 11
=n 1=×1500=300 r/min , 转向:逆向旋转 5p 5533
F φ7=×8. 56=12. 8 A , 22
60f 1n 11
==×1500=214. 3 r/min , 转向:正向旋转 7p 77
n 5=
4)7次谐波磁势幅值为
F 7=
转速
n 7=
(3)三相合成磁势的基波表达式为
↑ ↑
三、分数槽绕组与永磁同步电动机
1.分数槽绕组的应用
通常(若无特殊说明),一般交流电机所使用的绕组均为q =整数的整 数槽绕组。
分数槽绕组是交流电机绕组的一个重要组成部分。
一般分数槽绕组使用在大中型多极水轮发电机、低速同步电动机和一 部分异步电动机中。
其主要目的是为了解决电机转速较低、极对数较多而电机槽数又有限 的矛盾; 同时利用分数槽绕组的等效分布作用和对齿谐波反电势的削弱作 用,以达到改善电势波形和提高绕组利用率的效果。
采用分数槽绕组有如下优点:
⑴ 电枢冲片槽数较少,电枢铁心制造工艺相对简单;
⑵ 常采用集中绕组,槽利用率高、槽满率高,简化了嵌线工艺;
⑶ 当第一节距y 1= 1时,可采用自动绕线,不仅提高劳动生产率,又
降低了成本。
⑷ 一般采用分数槽绕组时,电机线圈端部较短,不仅节约了铜线,
而且同等情况下减少了电机铜耗。
⑸ 在不斜槽的情况下,减少了齿槽效应,改善电机的电势波形,大
大减少了电机静态和低速时的转矩波动。
2.分数槽绕组的对称条件
● 采用分数槽绕组时,每极每相槽数q 可以写成:
q = Z /(2pm ) = b +c /d = N /d (3-4)
式中,m - 相数;p - 极对数;Z - 电机铁心槽数;
b - 整数;c /d - 不可约真分数;
N /d -不可约分数,可以是真分数,也可以是假分数。
● 和整数槽绕组一样,分数槽绕组也有多种不同的构成方式;
按相带分可有60°相带绕组、120°相带绕组和大小相带分数绕组; 同样也有单层、双层绕组等。
● 在永磁无刷电动机和永磁伺服电动机中,在功率较小的情况下,采用最
多的是q 为不可约真分数的单、双层分数槽绕组,且尤以y 1=1的绕组使 用最多。
● 利用槽电势星形图分析时 整数槽电机绕组 在整数槽组中,电机
有p 对极,则有p 个重叠
的槽电势星形,每个电势
星形中所对应的槽在磁
极下分别处于相同的位
置,相当于电机由p 个单
元电机组成。 分数槽电机绕组 在分数槽组中,相邻磁极和定子槽的相对位置是不同的。但就整个电机来说,某些磁极和定子槽的相对位置可与另一些磁极和定子槽的相对位置所重复。根据分析,分数槽绕组的单元电机数t 为电机电枢槽数Z 与电机极对数p 的最大公约数,即有
Z = t Z ′,p = t p ′ (3-5)
其中,Z ′ - 单元电机的槽数;
p ′ - 单元电机的极对数。
借助槽电势星形图,经过分析后,不难得出单元电机中有:
q ′ = N , p ′ = p /d (3-6)
这就是说对任何m 相对称的双层分数槽绕组,在计算基波电势时,它和一个具有同样槽数q ′ = N 而极对数p ′ = p /d 的整数槽绕组是等效的。
由此得出m 相分数槽绕组的对称条件为:
Z ′/m = Z/(m t ) = 整数 (3-7)
或
d /m ≠ 整数,2p /(d ·a ) ≠ 整数 (3-8)
绕组的最大并联支路数为
a max = 2p ′ = 2p/d (3-9)
范文三:三相异步电机绕组结构
实训二 三相异步电机绕组结构
一、 有关术语和基本参数
(一)线圈和线圈组
1. 线圈
线圈是组成绕组的基本元件, 用绝缘导线(漆包线)在绕线模 上按一定形状绕制而成。一般由 多匝绕成,其形状如图1-2-1所 示。它的两直线段嵌入槽内,是 电磁能量转换部分,称线圈有效
边;两端部仅为连接有效边的“过 (a)菱形线圈 (b)弧形线圈 (c)简化画法 桥”,不能实现能量转换,故端部越 图1-2-1常用线圈及简化画法
长材料浪费越多;引线用于引入电流的接线。图1-2-2是线圈嵌入铁心槽内的情况。
(a)立体图 (b)展开图 (c)有效边在槽内实际情况
图1-2-2单层绕组部分线圈嵌入铁心槽内
2.线圈组
几个线圈顺接串联即 构成线圈组,异步电机中 最常见的线圈组是极相组。 它是一个极下同一相的几 个线圈顺接串联而成的一
组线圈,见图1-2-3所示。 (a)连接方法 (b)展开图 (c)简化图
图1-2-3 一个极相组线圈的连接方法 (二)定子槽数
1. 定子槽数
表示。如图1-2-2(a)、(b)所示的
和磁极数2
定子铁心上线槽总数称之为定子槽数,用字母就为电机定子铁心上的线槽。
2. 磁极数2
磁极数是指绕组通电后所产生磁场的总磁极个数,电机的磁极个数总是成对出现,所以电机的磁极数用2出磁极数,即
表示。异步电机的磁极数可从铭牌上得到,也可根据电机转速计算
式中
—电源频率; —磁极对数; —电机同步转速,
可从电机转速取整数后获得。
它在交流电机中为确定转速的重要参数,即
(r/min)
(三)极距τ和节距y
1. 极距τ
相邻两磁极之间的槽距,通常用槽数来表示
(槽)
2. 节距
一个线圈的两有效边所跨占的槽数。为了获得较好的电气性能,节距应尽量接近极距τ。即
(取整)
在实际生产中常采用的是整距和短距绕组。
(四)每极相槽数与槽距角
1. 每极相槽数
是指绕组每极每相所占的槽数
(槽)
2. 槽距角
指定子相邻槽之间的间隔,以电角度来表示,即
(电角度)
(五)线径与并绕根数
线径是指绕制电机时,根据安全载流量确定的导线直径。功率大的电机所用导线较粗,当线径过大时,会造成嵌线困难,可用几根细导线替代一根粗导线进行并绕。其细导
线根数就为并绕根数
(六)单层与双层绕组
单层绕组是在每槽中只放一个有 效边,这样每个线圈的两有效边要分 别占一槽。故整个单层绕组中线圈数
等于总槽数的一半。 1—槽楔;2—覆盖绝缘;3—槽绝缘;4—层间绝缘;
双层绕组是在每槽中用绝缘隔为 5—上层线圈边;6—下层线圈边;
上、下两层,嵌放不同线圈的各一有 图1-2-4 单、双层槽内布置情况 效边,线圈数与槽数相等,图1-2-4是单层、双层槽内布置情况示意图。
二、三相绕组的排列方法
为了在电机内形成旋转磁场,定子槽内各有效边应流过哪一相的电流是有规律的,对三相绕组进行排列其目的,就是体现规律,形成旋转磁场。
(一)三相绕组的构成规则
1. 每相绕组的槽数必须相等,且在定子上均匀分布; 2. 三相绕组在空间应相互间隔120电角度。
3. 三相绕组一般采用60相带,即三相有效边在一对磁场下均匀地分为6个相带。
(二)排列方法
1. 计算基本参数
每极相槽数;
槽距角
2. 编写槽号
编号从第一槽开始顺序编号。 3. 划分相带
。
取个槽为一个相带,相带按U1-W2-V1-U2-W1-V2的顺序循环排列。 4. 标定电流正方向
把U1、V1、W1相带电流正方向选定为指向上方,则U2、V2、W2相带电流正方向指向下方。即相邻相带的电流正方向上下交替。
5.作绕组表
图1-2-5是三个三相绕组分相带、标电流的排列情况。取不同的极数和槽数,以利于观察其规律。(a)图为三相4极24槽;(b)图为三相2极24槽;(c)图为三相4极36槽。
(a)3相4极24槽
(b)3相2极24槽
(c)3相4极36槽
图1-2-5 定子绕组有效边相带分布及各相电流正方向
只要按上述排列方法,使U1相带各槽导体流入U相电流;V1相带各槽导体流入V相电流;W1相带各槽导体流入W相电流,而U2相带、V2相带和W2相带对应的各槽导体分别流出U相、V相和W相电流,即可满足绕组空间对称的规则。
三、三相绕组的端部连接方式
连接端部是为了将分布在各相带的槽导体构成三相对称绕组,连接方式是多种的,每一种连接方式就形成一种形式的绕组。
(一)三相单层绕组端部连接方式性能及特点
1. 等宽度式(叠式)
线圈为等距,所有线圈节距相同,线模容易调整;线圈节距短于极距(整距),较省线材;单层绕组的线圈数目少,嵌线省时,但电气性能较差。
2. 同心式
绕组是单层布线,有较高的槽满率;线圈节距的平均值为等距,绕组端部长度大而耗线材,且漏磁较大、电气性能也较差;可采用分层嵌线而形成“双平面”或“三平面”绕
组,使嵌线方便,多适用于二极电机。
3. 交叉式
绕组为整距,但线圈平均节距较短,用线较节省;每组线圈数和节距都不等,给嵌线工艺增加了困难;槽满率较高,电气性能较差。另外,端部连接方式也可成为同心交叉式,即把等宽度的两线圈改成同心式。
(二)三相单层4极36槽绕组端部连接方式
由三相4极36槽可知该绕组的每极相槽数q=3,端部连接方式可能出现三种方式,用
图1-2-6(a)、(b)、(c)描绘,只连接其中某一相在各分图上说明。
(a)等宽式(叠式)
(b)同心式
(c)交叉式
图1-2-6 单层绕组的三种类型
在实际中,选用哪种端部连接方式,这不是修理人员所考虑的,只有设计人员才考虑。对修理人员来说,原设计数据是重绕电机的重要依据,是不可更改的。
(三)三相单层4极24槽绕组端部连接方式
由三相4极24槽的两个基本参数可计算出每极相槽数=2,根据其规则排列组合有三种端部连接方式,见图1-2-7所示。
(a)等宽式(叠式)
(b)同心式
(c)单链式
总之,以上几种单层绕组型式,具有高的槽利用率、不易发生相间短路、线圈数目较少、嵌线工时省等优点,在小型电机中得到广泛应用。常用的JO2及Y系列电机中,单层叠式绕组用于绕组用于
的4、6、8极电机;单层交叉式绕组用于
的2、4极电机;同心式
的2极电机。这些绕组型式在日常的修理工作中都经常可以见到。另外,
单层绕组由于结构的限定,其绕组端部较厚,不易整形,无法利用适当的短距来改善绕组的电磁性能,这就是单层绕组的电机性能较差的原因。
对容量大,要求高的电机,通常用双层绕组。双层绕组的节距可任意选定,利用适当的短距系数即可消除气隙磁场中的高次谐波,改善电机性能。
(四)三相双层绕组端部连接方式
双层绕组在每槽内嵌放两个有效边,形成了上层边与下层边,各层均有自身的分布规则。绕组的上层边仍按单层对称三相绕组的分相规则进行,划分出每对磁极下的U1-W2-V1-U2-W1-V2各相带,而下层边是按给定的节距
,确定每一线圈的下层边。节距
的确定可按原先设定值,在拆绕组时记录下来。也可计算确定节距:先由τ=
确定
极距, 再按取整数即可。最后用叠绕的方式连接各线圈端部。
双层绕组的每个线圈两个有效边一定要分别置于上层边和下层边,连接线圈端部组成极相组和相绕组所依据的电流正方向是按各线圈上层有效边所标定的,具体端部连接方式 见图1-2-8所示,图为三相4极36槽双层叠绕组。
(a)U相绕组
b)三相绕组
图1-2-8 双层叠绕组展开图
(五)三相双层叠绕组端部连接方式性能及特点 1. 性能
(a)由于能随意选择合理的节距,从而改善了电磁性能;
(b)线圈采用了短节距,使端部长度变小,省线材,并提高了效率. 2. 特点
(a)所有线圈节距相同,绕制方便; (b)线圈端部变形小,易整形;
(c)线圈数比单层绕组多一倍,故嵌线费工;
(d)在同一槽内由于嵌入异相线圈边,这样容易造成短路故障; (e)层间需加绝缘,槽满率就较低。
四、 实训要求
1. 搞懂60相带在磁极下按U1-W2-V1-U2-W1-V2规律排序的原因。
2. 补画出图1-2-6(a)、(b)、(c)各分图的其它两相的端部接线,并作出绕组表,最后再把三相绕组接为Y接。
3. 补画出图1-2-7各分图中其它两相的端部接线,作出绕组表,最后再把三相绕组接为△接,并将绕组接成二路并联的形式。
4. 会画三相双层叠绕36槽二极绕组端部连接图和展开图。
5. 对所要嵌线修理的三相异步电机,作出绕组表,画出绕组端部连接图和展开图。 体会“按分相后确定的各导体有效边内电流正方向连接”这句话,简练地总结出三相绕组端部连接的接线规律。
五、实训记录
1. 在图1-2-6、图1-2-7各分图上补画齐其它两相端部接线。
2. 本人所要嵌线修理的三相异步电机,绕组总线圈数= ,每极相槽数= ,极相组数= ,每组线圈数= ,线圈节距= ,极距= ,并联支路数= 。
作出绕组表
三相双层叠绕36槽2极电机展开图
4. 端部接线规律总结:
六、实训考核
实训项目量化考核表
范文四:【DOC】-三相交流电机的绕组讲义_图文
三相交流电机的绕组讲义_图文
第一讲 三相交流电机的绕组
一、三相交流电机及其绕组
1(三相交流电机的种类和结构
三相异步电机 鼠笼式 绕线式
三相同步电机 凸极式 隐极式
(定子均为三相交流绕组)
2(三相交流电机的工作原理
交流励磁磁场和直流励磁磁场
同步电动机的起动
3(三相交流绕组
(一)三相交流绕组的作用
三相交流绕组的作用
(二)三相交流绕组的要求
电磁方面
? 在绕组中通过三相对称电流时,气隙中有旋转磁场;
? 气隙中有旋转磁场时,绕组中感应产生对称的三相电势;
? 交流绕组的电势和磁势应为按正弦规律变化的时间波和空间波,
即其谐波分量尽可能小;
结构方面
? 三相交流绕组在空间作对称分布(即其轴线互差2π/3 电角度); ? 各相绕组的匝数应相相同。
(三)三相交流绕组的的基本概念
(1)极对数
a)一对极的三相交流绕组 b) 一对极磁场的磁力线 c)二对极的三相交流绕组 d) 二对极磁场的磁力线
(2)电角度
每对磁极对应360?电角度 ; 整个圆周上,360?机械角度。 一对极的 电角度为 360?
二对极的 电角度为 720?
p 对磁极的 电角度 , 机械角度 ? p (3-1)
二对极的 电角度为 720?
p 对磁极的 电角度 , 机械角度 ? p
? 12槽 ?
二对极的 电角度为 720?
p 对磁极的 电角度 , 机械角度 ? p
? 24槽 ? (3)相带
每极每相交流绕组在电枢圆周上连续占据的电角度称相带。
三相交流绕组通常为60? 相带。
(4)每极每相槽数
为使三相绕组感应电势对称,每相在每极下应占有相等的槽数, 该槽数
称每极每相槽数,用q表示。
? q = 2 ?
(3-2)
式中,m , 相数;
Z , 电枢圆周总槽数。
(5)整数槽与分数槽
(6)节距
一个线圈的两个线圈边之间沿电枢气隙圆周上的跨距称为节距, 用y1表
示。
节距可用长度单位表示,也可用槽数表示。
? 一般三相60相带双层绕组,取y1?(5/6)τ,以削弱5、7次谐
波。
(7)单层绕组
一个线圈有二个线圈边。
单层绕组在每槽内只安放一个线圈边。
? 单层绕组排列与串、并联
串联
(8)双层绕组 并联
习惯上,线圈的编号同其上层边所在的槽号。
(9)槽间角、极距
相邻两槽之间所间隔的电角度称为槽间角,以α1表示。
(3-3)
(10)三相绕组的排列 ? 每一相绕组的有效边都
是由放置在相同槽号
中的导体组成;
? 导体中电流规定的正方
向不变;
? 电磁作用相同。所不同
的是绕组端部的连接
方式。
(a)排列次序;(b)链式;(c)同心式;(d)交叉式
(11)三相绕组
? 一对极、集中、整距
槽数:Z = 6; 极对数:p = 1 极距:τ = Z,(2p) = 6,2 = 3;
每极每相槽数:q = Z,(2pm) = 6,(2?3) = 1 节距:y1 = Z,(2p) ? ε = 6,2?0 = 3 (整距,ε = 0,y1 = τ) A相线圈:1—4
B相线圈:3—6
C相线圈:5—2
? 一对极、分布、整距
链式
槽数:Z = 12; 极对数:p = 1 极距:τ = Z,(2p) = 12,2 = 6;
每极每相槽数:q = Z,(2pm) = 12,(2?3) = 2
节距:y1 = Z,(2p) ? ε = 12,2?0 = 6 (整距,ε = 0,y1 = τ)
A相线圈(2个):1—7、2—8; A相线圈组(1个):1—7—2—8; B相线圈(2个):5—11、6—12; B相线圈组(1个):5—11—6—12; C相线圈(2个):9—3、10—4; C相线圈组(2个):9—3—10—4;
同心式
槽数:Z = 12; 极对数:p = 1
极距:τ = Z,(2p) = 12,2 = 6;
每极每相槽数:q = Z,(2pm) = 12,(2?3) = 2
A相线圈(2个):1—8、2—7; A相线圈组(1个):1—8—2—7; B相线圈(2个):5—12、6—11; B相线圈组(1个):5—12—6—11; C相线圈(2个):9—4、10—3; C相线圈组(2个):9—4—10—3;
交叉式
槽数:Z = 12; 极对数:p = 1
极距:τ = Z,(2p) = 12,2 = 6;
每极每相槽数:q = Z,(2pm) = 12,(2?3) = 2
A相线圈(2个):2—7、8—1; A相线圈组(1个):2—7—1—8; B相线圈(2个):6—11、12—5; B相线圈组(1个):6—11—5—12; C相线圈(2个):4—9、10—3; C相线圈组(1个):9—4—3—10;
? 四、二对极、分布、整距
槽数:Z = 36; 极对数:p = 2
极距:τ = Z,(2p) = 36,4 = 9(槽);
每极每相槽数:q = Z,(2pm) = 36,(4?3) = 3
A相线圈(6个):1—10、2—11、3—12、19—28、20—29、21—30; A相线圈组(2个):1—10—2—11—3—12;19—28—20—29—21—30; B相线圈(6个):7—16、8—17、9—18;25—34、26—35、27—36; B相线圈组(2个):7—16—8—17—9—18;25—34—26—35—27—36; C相线圈(6个):13—22、14—23、15—24;31—4、32—5、33—6; C相线圈组(2个):13—22—14—23—15—24;31—4—32—5—33—6;
槽间角:α1 = 2pπ/ Z = 4?180?/36=20?;
基波分布系数:kq1 =,Sin(qα1/2),,,qSin(α1/2),
=,Sin(3?20?/2),,,3?Sin(20?/2),= 0.96
基波绕系数:kN1 = kq1 ky1= 0.96?1= 0.96 三次谐波分布系数:kq3 =,Sin(qνα1/2),,,qSin(να1/2),
=,Sin(3?3?20?/2),,,3?Sin(3?20?/2),= 0.67
三次谐波绕系数:kN3 = kq3 ky3= 0.67?1= 0.67 五次谐波分布系数:
kq5 =,Sin(qνα1/2),,,qSin(να1/2),
=,Sin(3?5?20?/2),,,3?Sin(5?20?/2),= 0.22
五次谐波绕系数:kN5 = kq5 ky5= 0.22?1= 0.22 ? 二对极、分布、短
距
(不完整)
(比较)
节距:y1 = 7(槽);
(A相完整,B、C不完整)
槽数:Z = 36; 极对数:p = 2
极距:τ = Z,(2p) = 36,4 = 9(槽);
每极每相槽数:q = Z,(2pm) = 36,(4?3) = 3
A相线圈(12个):1—8、2—9、3—10、 19—12、18—11、17—10、 19—26、20—27、21—28、1—30、36—29、35—28。 A相线圈组(4个):1—8—2—9—3—10; 19—12—18—11—17—10; 19—26—20—27—21—28;1—30—36—29—35—28。
(A、B相完整, C不完整)
B相线圈(12个):7—14、8—15、9—16、 25—18、24—17、23—16; 25—32、26—33、27—34、 7—36、 6—35、 5—34。 B相线圈组(4个):7—14—8—15—9—16;25—18—24—17—23—16; 25—32—26—33—27—34、 7—36—6—35—5—34。
(完整)
C相线圈(12个):13—20、14—21、15—22、31—24、30—23、29—22、 31—2、 32—3、 33—4、 13—6、 12—5、 11—4。 C相线圈组(4个):13—20—14—21—15—22;31—24—30—23—29—22; 31—2—32—3—33—4、 13—6—12—5—11—4。
基波短距系数:ky1 = Sin,πy1/(2τ),= Sin,180??7/(2?9),= 0.94 基波绕系数:kN1 = kq1 ky1= 0.96?0.94 = 0.90
三次谐波短距系数:ky3 = Sin,νπy1/(2τ),= Sin
,3?180??7/(2?9),= -0.5 三次谐波绕系数:kN3 = kq3 ky3= 0.67?(-0.5) = -0.335 五次谐波短距系数:ky5 = Sin,νπy1/(2τ),= Sin,5?180??7/(2?9),= -0.17 五次谐波绕系数:kN5 = kq5 ky5= 0.22?(-0.17)= -0.04
? 二对极、分布、短距(又例)
2p=4,Z=48,y1=9,a = 2,每极每相槽数q = Z/(2pm) = 48/(4?3) =
4, 极距:τ = Z,(2p) = 48,4 = 12(槽);
A相线圈(16个):1—10、2—11、3—12、4—13、 25—16、24—15、23—14、22—13、 25—34、26—35、27—36、28—37、 1—40、48—39、47—38、46—37。 A相线圈组(4个):1—10—2—11—3—12—4—13; 25—16—24—15—23—14—22—13; 25—34—26—35—27—36—28—37; 1—40—48—39—47—38—46—37。
A相支路数(2个):1—10—2—11—3—12—4—13—25—16—24—15—23—14—22—13; 25—34—26—35—27—36—28—37—1—40—48—39—47—38—46—37;
B相线圈(16个):9—18、10—19、11—20、12—21、
33—24、32—23、31—22、30—21、
33—42、34—43、35—44、36—44
9—48、8—47、7—46、6—45。
B相线圈组(4个):9—18—10—19—11—20—12—21;
33—24—32—23—31—22—30—21、
33—42—34—43—35—44—36—44
9—48—8—47—7—46—6—45。
B相支路数(2个):9—18—10—19—11—20—12—21—33—24—32—23—31—22—30—21; 33—42—34—43—35—44—36—44—9—48—8—47—7—46—6—45
。
C相线圈(16个):17—26、18—27、19—28、20—29、
41—32、40—31、39—30、38—29、
41—2、42—3、43—4、44—5、
17—8、16—7、15—6、14—5。
C相线圈组(4个):17—26—18—27—19—28—20—29、
41—32—40—31—39—30—38—29、
41—2—42—3—43—4—44—5、
17—8—16—7—15—6—14—5。
C相芝路数(2个):17—26—18—27—19—28—20—29—41—32—40—31—39—30—38—29、 41—2—42—3—43—4—44—5—17—8—16—7—15—6—14—5。 二、三相交流绕组的磁势
? ? * 一相集中整距绕组的磁势
单个整距线圈磁势的波形
将此矩形波用傅氏级数进行分解,得基波和各次谐波的幅值为
Fcν=
1π2?
νπ2π0fc(x)cosνxdxIcNc =sinνπ
2
式中,v=1,3,5,7, ...。当v=1时,Fc1为基波磁势的幅值;此外,
值。
若把空间坐标Fcν为v次谐波磁势的幅x(机械弧度)也改用对基波的电角度α表示,则由一个整距线圈构成相绕
组的磁势的表达式为
fc(t,α)=22111??IcNc?cosα?cos3α+cos5α?cos7α+.......?sinωt (7-1) π357??
其中,基波磁势为
fc1(t,α)=
其最大值为 Fc1=22πIcNccosαsinωt (7-2) 2πIcNc=0.9IcNc (7-3)
v次谐波磁势为
fcν(t,α)=
其最大值为 1?22νπ?INsincc2ν??π???cosνα?sinωt (7-4) ??
Fcν?1?22?IcNc?=?? (7-5) ν?π?
可见,分解后的磁势基波和各次谐波既是时间角ωt的函数,又是空间角α的函数。
* 线圈的分布和短距对磁势的影响
实际交流电机的交流绕组为了充分利用铁芯通常采用沿定子圆周分布排列的。本节将讨论绕组的分布和短距对绕组磁势的影响。
一、线圈分布的影响
在交流电机中,无论单层绕组或双层绕组,每相绕组都是由若干个线圈串联或并联组成。就产生磁势的效应而言,不论具体的线圈结构如何,都可等效地认为每个线圈组由若干个节距相等、匝数相同、依次沿定子圆周错开一个角度(通常为一个槽距角)的线圈串联而成。
图7,5所示为三个线圈串联的线圈组。各线圈沿定子,圆周依次位移一个槽,对基波来说为α1电角度,如图7,5(a)所示。则各线圈磁势的v次谐波依次在空间上位移vα1电角度。
r用空间矢量表示时,各线圈的v次谐波磁势矢量Fcν依次有一空间相位差vα1,如图7,5(b)
r所示。于是用矢量相加可求得该线圈组磁势的v次波幅值Fqν如图
7,5 (c)所示。
由三个线圈串联的线圈组磁势的ν次波 图7,5
(a)多线圈的空间位置;(b) 多线圈的ν次波磁势矢量;(c) 线圈组的ν次波磁势矢量
显然,Fqν< qfcν。这一减小可用一个分布系数kqν来体现。="">
定义
kνq
q=Fν qνqccq为交流绕组磁势空间v次波的分布系数。即 Fν=qFνkν (7,6)
式中,kqν可由图7,5(c)中的矢量的几何关系求得
kν=qsinqν1
qsinν1
2 (7-7)
当v=1时, k
即为基波的分布系数。
当q相当多时, sinq12 (7-8) =q1qsin12
kν=qsinνπ6 6
v=1, kq1 = 3/π = 0.955
v=3, kq3 = 2/π = 0.637
v=5, kq5 = 3/(5π) = 0.191
......
以此类推,可见当v不太大时,kqν随v的次数增加而明显衰减。因此说,利用绕组的分布排列可有效地削弱谐波磁势,改善交流绕组磁势波形,使之接近正弦波。
二、线圈短距的影响
如前所述,y1为线圈的两线圈边之间的节距,τ为极距,当y1<τ时称短距。通常在 双层绕组中采用之。="">
定义 β=
称为相对节距。
短距线圈缩短的距离为yτ1 τ-y1,缩短距离的相对值为τ?τy1=1?β=ε或π?
πy1=1?β=ε 。 比较两个整距和短距线圈的磁势,见图7,6所示
图7,6 两个线圈的磁势
(a) 两个整距线圈的磁势;(b) 两个短距线圈的磁势
rr图7―6 (a) 中两个整距线圈11 和22的磁势分别为Fc1和Fc2,两矢量大小相等、方向
r’’相同,其合成磁势为Fy,即Fy=2Fc1=2Fc2。图7,6( b)中两个短距线圈11 和22产生的磁
rr’’势可等效为由两个整距线圈12和12所各自产生的磁势Fc1和Fc2。这两个矢量不同向,其合’’
成磁势为yε。显然,Fyε,Fy 。同样,这一减小的折扣可用一个短距系数kyν来体现。
定义: kνy=Fε y
y
为交流绕组磁势空间v次波的短距系数。
由图7-6 (b)的几何关系可得
F
则 yε=2Fc1COSνεπ2
Fε=COSνεπ kν=2Fy
y
y=sinνπy12τ (7,9)
式中 v=1,3,5,7 ...。
当v=1时,
ky1=COSεπ2=sinπy1
2τ (7,10)
称为基波短距系数。
利用绕组的短距可以有效地削弱谐波磁势,使之接近正弦波。通常取 y1?5τ/ 6
分布系数和短距系数的乘积为绕组数系数,即
kNν= kqν?kyν (7,11) 式中,kNν?? 交流绕组磁势空间v次谐波的绕组系数。
当v=1时,
12) kN1= kq1?ky1 (7,
称为基波绕组系数。
* 单相绕组的磁势
一、单相脉振磁势
对于p对极的整数槽绕组,设每相绕组总匝数为Nφ,则每相每对极串联匝数为Nφ绕组的导体内电流有效值为Ic,根据前面分析的结果可得每相每极基波磁势为
/p。
fφ(t,α)=
1
22
π
I
N
C
φ
p
k
N1
COSα?sinωt
每相电流有效值为I,每相有a条支路,每相每条支路的串联匝数为N,
则Ic=I/a, Nφ=
aN。于是,每相每极基波磁势为
2()t,α=fφ1
πINp
k
N1
COSα?sinωt
(7,13)
每相每极基波磁势的最大值为
Fφf
1
=
2
2INπp
k
(
N1
=0.9
IN
p
k
N1
(安/极) (7,14)
每相每极v次谐波磁势为
φν
(t,α)=
2
2INπνp
k
Nν
sin
νπ
2
COSνα?sinωt
(7-15)
每相每极v次谐波磁势的最大值为
Fφν
=
2
INπνp
k
Nν
=0.9
INνp
k
Nν
=
1
ν
NνN1
Fφ
1
(安/极)
(7,16)
综合以上分析可得出如下结论:
一相交流绕组产生的磁势为一个脉振磁势。该磁势脉振频率与绕组内正弦波电流频率相同,为f1。该磁势沿气隙圆周近似地按梯形分布,它可按空间角分解为基波和一系列谐波。基波和每个谐波空间位置不变,而波幅以同一频率f1按正弦规律交变。当绕组内电流为非正弦波时,可按时间角将它分解为基波和一系列谐波。这些波各自对应有以空间角分解的基波和各次谐波的磁势。
为了改善电机性能,应设法削弱磁势中的谐波,常采用短矩和分布绕组来实现。 二、脉振的相绕组磁势分解为两个旋转磁势
对于脉振的基波磁势可分为两个幅值相等、速度相同但方向相反的旋转磁势:
fφ(t,α)=FφCOSα?sinωt
1
1
1
=Fφ1[sin(ωt?α)+sin(ωt+α)]=2
f
+
+
f
?
式中,
f+=
1
Fφ1 sin (ωt-α) 2
1
Fφ1 sin (ωt+α) 2
是一个正转的旋转磁势,即其幅值不变,其幅值的位置随时间不断沿α增大的方向移动;而
f?=
是一个反转的旋转磁势,即其幅值位置随时间不断沿α减小的方向移动。
旋转磁势f+、f?的幅值均为
Fφ
2
1
;其转速由绕组内电流角频率ω及绕组的极对数p决定,
为
60f
(r/min)。 p
正、反转的旋转磁势f+、f,的物理意义可解释为:在ωt–α =
π
2
情况下,f+ =
1
Fφ1为2
其幅值;在ωt + α =
π
2
情况下,f, =
1
Fφ1为其幅值。也就是说,对应不同的时刻t,这二2
个旋转磁势的幅值位置(α)也不同。正转的旋转磁势f+ 随时间推移沿顺相序方向移动,故谓正转;反转的旋转磁势f, 随时间推移沿逆相序方向移动,故谓反转。表7-1、表7-2和图7-7给出正、反转的旋转磁势f+、f,在几个时刻对应的幅值位置。
表7-1 正转的旋转磁势f
的几个幅值位置
表7-2 反转的旋转磁势f–的几个幅值位置
(a) (b) (c)
(d) (e)
图7-7 正、反转旋转磁势f+ 、f–的几个幅值位置
(a)ωt = 0时;(b)ωt =
π
2
时;(c)ωt = π时;(d)ωt =
3
π时;(e)ωt = 2π时; 2
同理,对于每次谐波脉振磁势也可以各自分解为两个幅值相等、速度相同
但方向相反的旋转磁势:
f
φν
(t,α)=(Fφνsinνπ
2
)COSνα?sinωt
1=2
Fφνsin
νπ
2
[sin(ωt?να)+sin(ωt+να)]
第四节 三相交流绕组的合成磁势
一( 基波磁势
设三相交流绕组内通过的三相电流如图7-8所示,分别为
i i
A
==
222
III
C
sinωt sin(ωt?120sin(ωt?
240
o
BC
) )
iC=
o
C
图7-8 三相电流
三相交流绕组在空间分布互差120?电角度,则三相交流绕组的其波磁势
分别为
fff
A1
===
22
2INπp
kkk
N1
sinωtcosα
B1
INπp2INπp
sinωt?120N1
sinωt?N1
(
o
)cos(α)cos(α
)]
??
?120?
o
)
o
2
C1
(
240
o
240
)
(7,17)
将各相脉振磁势分解为二个旋转磁势
fff
A1
=
B1
C1
1
21=21=2
FFF
φ1
[sin(ω
t?αt?αt?α
)+)+)+
sinsinsin
(ω
t+α
φ1
φ1
[sin[sin
(ω(ω
(ωt+α(ωt+α
240120
o
o
)])]
(7-18)
三相交流绕组合成磁势的基波为 f1(t,α)= fA1+ fB1+ fC1 =
3 2
Fφ1 sin(ωt-α)
=F1sin(ωt-α) (7,19) 这是一个波幅值恒定圆形的旋转磁势,如图
7-9所示。 式中
3?22IN3
? F1 = Fφ1 = ?
2?2πp?
=1.35
?32IN
kN1??=π?p
?
k
N1
INp
k (安/极) (7,20)
N1
为三相交流绕组合成磁势基波的最大值。其值为每相脉振磁势波波幅的
3
倍。其转向为正相序,2
即幅值位置从A相绕组轴线(图7-9中的A轴)转向相位滞后120的B相
绕组轴线(图7-9中的B轴),再转向C相绕组轴线(图7-9中的C轴)。
合成磁势波的转速为
n1=
60f
(r/min) (7,21) p
称同步速。
由图7-9显见:当某相绕组内的电流达到最大值时,三相合成磁势基波幅值位置恰在该相绕组的轴线上。
二、谐波磁势
三相交流绕组v次谐波磁势
νπ?
?Fφνsin?sinωtcosναfν(t,α)=?
2??
A
νπ?
ν(α?120)] ?Fφνsin?sin(ωt?120)cos[fν(t,α)=?
2??
o
o
B
νπ?oo?
()()[(t,α=sinsinωt?cosνα???fCν240240)]Fφν
?
2?
各相脉振磁势分解为二个旋转磁势
fAν= fBν=
1νπFφν sin,sin(ωt-vα)+sin(ωt+vα), 221νπFφνsin22
?sinωt?
120?
??+sinωt?120
(
o
(
?να
o
+ν
+να
120
?ν120
?
o
)
oo
)
o
?? ???? ??
1νπ
fCν=Fφνsin
22
对于三次谐波
?sinωt?
240?
??+sinωt?240
(
o
(
?να
o
+ν
+να
240
ν240
)
)
1
[ sin(ωt- 3α)+ sin(ωt+3α)] 2Fφ31
fB3(t,α)=-Fφ3[ sin(ωt-3α-1200)+ sin(ωt+3α-1200)]
21
fC3(t,α)=-Fφ3[ sin(ωt-3α-2400)+ sin(ωt+3α-2400)]
2
fA3(t,α)=-
三相交流绕组合成磁势的三次谐波为
f3(t,α)= fA3 + fB3 + fC3 = 0
由此可分得出如下结论:三相交流绕组的三次及三的整数倍次谐波合成磁势均为零。 对于五次谐波
1[sin(ωt-5α)+ sin(ωt+5α)] 2Fφ5
1 fB5(t,α)=Fφ5[sin(ωt-5α+1200)+ sin(ωt+5α)] 2
1 fC5(t,α)=Fφ5[sin(ωt-5α+2400)+ sin(ωt+5α)] 2 fA5(t,α)=
三相交流绕组合成磁势的五次谐势为
f5(t,α)=fA5 +fB5 +fC5 =3sin(ωt+5α) 2Fφ5
7,22) = F5 sin(ωt+5α) (
其最大值为
F5 = 332IN?= kFφ5N52π5p
IN (安/极) (7,23) kN55p =1.35
由此可见,三相交流绕组的五次谐波合成磁势是一个波幅恒定、逆基波磁势转向的旋转磁势,即与基波转向相反,其转速为 n5=51=60f (r/min) (7,24) 5p
旋转波的波长为基波的
对于七次谐波 1,全圆周共有5对极。 5
1[ sin(ωt-7α)+sin(ωt+7α)] Fφ72
10 fB7(t,α)=-Fφ7[ sin(ωt-7α)+ sin(ωt+7α-240)] 2
1 fC7(t,α)=-Fφ7[ sin(ωt-7α)+ sin(ωt+7α-1200)] 2 fA7(t,α)=-
三相交流绕组合成磁势的七次谐势为
f7(t, α)= fA7+ fB7+ fC7 =-3sin(ωt-7α) 2Fφ7
= - F7 sin(ωt- 7α ) (7,25) 其最大值为
F7 =3ININ?1.35== kkFφ7N7N72π7p7p
1N7(安/极) (7,26) F71N1=
可见,三相交流绕组的七次谐波合成磁势是一个波幅恒定的正向旋转磁势,即转向与基波相同,其转速为
n7=71=60f (r/min) (7,27) 7p
(a) (b)
(c) (d)
(e) (f)
图7-9 三相绕组基波合成磁势
(a) ωt = 0时,iA= 0;(b) ωt = 90时,iA= Im;(c) ωt = 150时;(d) ωt = 210时,iB= Im; 000
(e) ωt = 270时;(f) ωt = 330时,iC= Im00
综上所述,对称三相交流绕组合成磁势中包含有v= 6k?1(k=1、2、3、......) 次谐波。一般地说,当对称m相电流通过对称m相绕组时,绕组合成磁势中包含着下列次数的高次谐波:
v=2mk?1 (7,28) 式中k =1、2、3、...;当取加号时,谐波磁势转向与基波的转向相同。
谐波磁势(或相应的谐波磁场〕的存在,在交流电机中引起附加损耗、振动和噪声等不良影响,对异步电动机还将引起附加转矩,使电动机的起动性能变坏。因此,在设计电机时应尽量削弱磁动势中的高次谐波,采用短距和分布绕组是达到这个目的的很重要方法。
例7-1 有一个三相单层同心式绕组,2p=2,Z=24,其一相的端部联接画如图7-10所示,属同一相带的线圈出槽后端接线分向二侧弯走,若每个线圈的匝数相同,其基波绕组系数是多少,
图7-10
解 把该绕组看作是等效的整距分布绕组:
每极每相槽数 q=4 , 短距系数 ky1=1
则基波绕组系数即是分布系数 kN1sin30osin30o=kq1===0.958
oo30304sinqsinq4
例7-2 一台50000 kW的2极三相汽轮发电机,50Hz,UN, 10.5 kV,Y联接,cos?N, 0.85,定子为双层叠绕组,Z = 72槽,每个线圈一匝,y1,,τ,,,a = 2。试求当定子电流为额定值时,三相合成磁势的基波、3、5、7次谐波的幅值和转速,并说明转向。
解 I=IN=PN
UNCOS?N=500003?10.5?0.85 = 3234.46 A
τ=Z72==36槽 , 2p2
Z72==12 2pm2?3
2pqNc2?12?1==12匝 a2 q=N=
y1=5τ5?36==30 66
p?360o1?360o
α1===5o, 72Z
kN1qα112?5osinsiny130oo22=sin(90?)?=sin90??=0.9227
o36τ5qsin112?sin22
kN3qνα112?3?5osinsiny1?30???oo=?0.4514 =sin?3?90???=sin?3?90???oτ?36?3?5??qsin112?sin22
同理求得
kN5=0.0498, kN7=0.3007
F1=1.35?
F3=0
F5=1.35?NI12?3234.46?kN1=1.35??0.9227=48347.9 安匝/极 p1NI12?3234.46?kN5=1.35??0.0498=52.4安匝/极 5p5
NI12?3234.46?kN7=1.35??0.3007=2250.9安匝/极 7p7 F7=1.35?
n1=60f60?50==3000 r/min(转向:顺相序正转) p1
三相合成的三次谐波磁势为零,所以也不存在转速n3
n5=n13000==600 r/min(转向:逆相序反转) 55
n13000==428.6 r/min(转向:顺相序正转) 77n5=
例7-3 三相异步电动机,定子绕组为双层短距绕组,Y联接,槽数Z = 48,极数2p = 4,线圈节距y1=10,线圈匝数Nc=22匝,每相并联支路数a=4,通入电流I=37A,频率f=50Hz。试求:
(1)一相绕组磁势的基波和3次谐波的幅值,写出各项基波磁势的表达式;
(2)三相绕组合成磁势的基波和3、5、7次谐波的幅值,转速及转向;
(3)写出三相合成磁势基波的表达式。
解 (1)一相绕组的磁势为脉动磁势,各次谐波磁势的幅值为
Fφv=0.9
每极每相槽数 kNνN1kNI=0.9??NνI pνvp
Z48p?360o2?360oq===4, 槽距角 α===15o 2pm4?3Z48
极距
τZ
p=2p=48
4=12 ,
基波分布系数
sinqα4?15o
kq1=2sin
=2=0.958
qsin15o
24sin2
基波短距系数
ky1
y1=sinτ?90o=sin10
12?90o=0.966
p
基波绕组系数
kN1=kq1ky1=0.958?0.966=0.925
每相串联匝数列
N=2pqNc
a=4?4?22
4=88 匝
基波磁势幅值
F0.9kw1N0.9?0.925
φ1=pI=?88?37
2=1355.3(A)
3次谐波分布系数
sinq3αsin4?3?15o
kq3===0
qsin24sin3?15o.65
2
3次谐波短节距系数
ky110
y3=sinτ?3?90o=sin
p12?270o=?0.707
3次谐波绕组系数
kwN3=kq3ky3=0.65?(?0.707)=?0.46
3次谐波磁势幅值
F0.9kN5N
φ3=3pI=0.9?(?0.46)?88?37
3?2=?224.66
各相的基波磁势表达式为
fA=1355.3sinxsinωt
fB=1355.3sin(x?120o)sin(ωt?120o)
fC=1355.3sin(x+120o)sin(ωt+120o)
(2)求三相合成磁势幅值、转速及转向
1)基波磁势幅值为 F1=3
2F3
φ1=2?1355.3=2033,
转速 A
n1=60f60?50==1500 r/min (转向:正向旋转) p2
2)3次谐波合成磁势为零;
3)5次谐波磁势幅值为
F5=
转速 3?15.53=23.3 A, 2
60f11=n1=?1500=300 r/min , 转向:逆向旋转 5p55
33Fφ7=?8.56=12.8 A, 22
60f1n11==?1500=214.3 r/min , 转向:正向旋转 7p77n5=4)7次谐波磁势幅值为 F7=转速 n7=
(3)三相合成磁势的基波表达式为
? ?
三、分数槽绕组与永磁同步电动机
1(分数槽绕组的应用
通常(若无特殊说明),一般交流电机所使用的绕组均为q =整数的整 数槽绕组。
分数槽绕组是交流电机绕组的一个重要组成部分。
一般分数槽绕组使用在大中型多极水轮发电机、低速同步电动机和一 部分异步电动机中。
其主要目的是为了解决电机转速较低、极对数较多而电机槽数又有限 的矛盾;同时利用分数槽绕组的等效分布作用和对齿谐波反电势的削弱作 用,以达到改善电势波形和提高绕组利用率的效果。
采用分数槽绕组有如下优点:
? 电枢冲片槽数较少,电枢铁心制造工艺相对简单;
? 常采用集中绕组,槽利用率高、槽满率高,简化了嵌线工艺;
? 当第一节距y1= 1时,可采用自动绕线,不仅提高劳动生产率,又
降低了成本。
? 一般采用分数槽绕组时,电机线圈端部较短,不仅节约了铜线,
而且同等情况下减少了电机铜耗。
? 在不斜槽的情况下,减少了齿槽效应,改善电机的电势波形,大
大减少了电机静态和低速时的转矩波动。
2(分数槽绕组的对称条件
? 采用分数槽绕组时,每极每相槽数q可以写成:
q = Z,(2pm) = b,c,d = N,d (3-4)
式中,m , 相数;p , 极对数;Z , 电机铁心槽数;
b , 整数;c,d , 不可约真分数;
N,d ,不可约分数,可以是真分数,也可以是假分数。
? 和整数槽绕组一样,分数槽绕组也有多种不同的构成方式;
按相带分可有60?相带绕组、120?相带绕组和大小相带分数绕组; 同样也有单层、双层绕组等。
? 在永磁无刷电动机和永磁伺服电动机中,在功率较小的情况下,采用最
多的是q为不可约真分数的单、双层分数槽绕组,且尤以y1=1的绕组使 用最多。
? 利用槽电势星形图分析时 整数槽电机绕组 在整数槽组中,电机
有p对极,则有p个重叠
的槽电势星形,每个电势
星形中所对应的槽在磁
极下分别处于相同的位
置,相当于电机由p个单
元电机组成。 分数槽电机绕组 在分数槽组中,相邻磁极和定子槽的相对位置是不同的。但就整个电机来说,某些磁极和定子槽的相对位置可与另一些磁极和定子槽的相对位置所重复。根据分析,分数槽绕组的单元电机数t为电机电枢槽数Z与电机极对数p的最大公约数,即有
Z= t Z′,p = t p′ (3-5)
其中,Z′ , 单元电机的槽数;
p′ , 单元电机的极对数。
借助槽电势星形图,经过分析后,不难得出单元电机中有:
q′ = N , p′ = p,d (3-6)
这就是说对任何m相对称的双层分数槽绕组,在计算基波电势时,它和一个具有同样槽数q′ = N而极对数p′ = p,d的整数槽绕组是等效的。
由此得出m相分数槽绕组的对称条件为:
Z′,m = Z,(mt) = 整数 (3-7)
或
d,m ? 整数,2p,(d?a) ? 整数 (3-8)
绕组的最大并联支路数为
amax= 2p′ = 2p,d (3-9)
范文五:电机绕组阻值在线测量的自激问题和对策
电机绕组阻值在线测量的自激问题和对策
文章编号:1001.9944(2006)05.0013.04
电机绕组阻值在线测量的自激问题和对策
王文斌
(上海交通大学自动化系,上海200030)
摘要:文章介绍了异步电动机绕组阻值在线测量中.由隔直流电容引起异步电动机
的自激
问题.分析了产生的原因,并提出避免异步电动机自激问题的方案及电容选取方
法.
:绕组阻值;自激现象;在线测量;异步电动机 关键词
中图分类号:TM934文献标志码:A
CountermeasureAgainstSelf-excitationofOnlineWindingResistance MeasurementofanMotor
WANGWen.bin
(DepartmentofAutomation,ShanghaiJiaotongUniversity,Shanghai200030,China) Abstract:Itisintroducedthatseriescapacitorsmayarouseself-excitationwhileonlinewindin
gresistancemeasurementof
anasynchronousmotor.Itisanalyzedhowitarises,andthenthecountermeasureandselection
ofseriescapacitorsisput
forward.
Keywords:windingresistance;self-excitation;onlinemeasurement;asynchronousmotor
异步电动机绕组阻值是旋转电机标准(文献『31)
中的性能试验的一个测量参数,根据这个参数可以推
算出电机绕组温度及温升.电机绕组的在线测量是
指:在不中断交流负载电流的情况下,在负载电流上
叠加一微弱直流测量电流,再测量出绕组上的直流电
压,便可计算出绕组阻值.绕组阻值在线测量不仅可
以实时监测绕组阻值,绕组温度及温升,而且可以满 足一些特殊测量要求,具有广泛的实际用途.但是为 了准确测量绕组阻值,在主电路中必须串联一个隔直 流电容,从而可能引起电动机工作状态发生变化,严 重时会损坏电动机.所以电容的选取至关重要. 1基本测量方法
异步电动机绕组阻值在线测量原理图如图l. KM1电容C
电机
图1测量原理图
Fig.1Measurementcircuitdiagram
测量电路的结构分为两部分:一部分是直流电 阻测量电路,另一部分是隔直流电容.
直流电阻测量电路是在异步电动机绕组上加入 收稿日期:2006—02—20:修订日期:2006—06—28 作者简介:王文斌(1975一),男,在职研究生,研究方向为控制工程.
自动化与仪表2006(5)田
一
个微弱的直流恒流电流,再测量出电机绕组两端 直流电压,便可计算出电机绕组的阻值.而滤波器是 低通滤波器,为了阻止交流分量流入直流测量系统. 在异步电动机主回路中串联一个电容.是为了 阻止交流电源中的直流分量流入电机.否则将影响 测量准确性.如果是三相电机则每一相上都需要串 联一个电容
2自激问题分析
由于主电路中存在着一个电容,根据文献『l1, 异步电动机运行时可能产生自激现象.如果出现自
激现象可能会使电机无法运行,或不能运行在额定 转速下,严重时还可能会损坏电机.所谓自激现象, 就是一种电机和电网的机电参数的共振现象.当电 动机正常运行时,可以将电动机等效为r电路.所 以,为了便于了解这种自激现象的物理特征.先讨论 一
下r—L—C串联电路产生振荡的条件.见图2 C
图2-L—C旱联电路
Fig.2只.L—Ccircuitdiagram 根据文献[4]可知,r—L—C串联电路中的电流: i=i+
式中:是由电源决定的稳态电流分量;i是刚上电 时的瞬变电流分量.
1)对于稳态电流分量=
—F==sin(w,+),是一个偏移角.
,/(wL一)
当wL?时,可以忽略电容C对稳态电流oJG 分量的影响.
2)对于瞬变电流分量.e+A2en,A.和A2为 待定系数,P.和P是该电路特征方程的根. 厂r—
a.当r<2,/时,瞬变电流分量将由两个按指 数规律变化的电流分量组成.最后衰减为零; 厂—
b?当r>2,/时,瞬变电流分量幅值按指数规 田
律衰减的交变电流,最后衰减为零:
C.当r=O时,瞬变电流分量为幅值不衰减的交
变电流,其自振荡频率W.的值将和电路的共振频率 广—一
,/相同.Y上JL
从能量角度来看,电感和电容都是储能元件,而 电阻则是耗能元件.当r>O时,电路中的能量在电感 和电容之间交换,并逐渐消耗在电阻上,而且电阻越 大,能量消耗过程越快.当r=O时,耗能元件不存在 了.电感储存的磁能和电容储存的电能在交换过程 中没有任何消耗,其电流分量作不衰减的等幅振荡. 所以,电路产生稳态等幅振荡的必要条件是总回路 电阻为零.
由上述分析,只要满足r?0.瞬变电流分量就 可衰减为零,电机就能正常运行.但是问题是电机不 能完全等效为一个定值的卜L电路.根据电机学,电 机的等效电路如图3.
r:l2
Z尺(
s)+j(s)尺尺s
图异步电动机的等效电路
?
其中:电机定子电阻;
.——电机定子漏电抗;
X厂电机转子漏电抗;
..广__电机励磁漏电抗;
R厂转子电阻;
s——转差率,其值与转速相关.
异步电动机的电阻及电抗和转差率有关,特 别是在起动过程中,它的电阻及电抗均为变数.当转 差率为负值时,等效电阻R(s)也为负值,所以可能
使r—L—C串联电路中的总电阻为零.因此,如果参 数匹配不当时,就有可能构成等幅震荡的条件,形 成自激现象.此时,定子电流中也有两个分量,一 个是由电源决定的自由电流分量,其转差率为正, 处于异步电动机状态;另一个是由电容和电机参 数决定的频率为的自由分量,其转差率为负,处 于异步发电机状态.一般情况,频率略小于电源 频率.
当异步电动机出现自激现象时,其平均电磁转 矩也由两部分组成:一部分是基频电流产生的平均 电磁转矩:另一部分是m频电流产生的平均电磁转 矩前者是电动机作用的正转矩,后者是发电机作用 的负转矩,而且由于两者的频率不同,从而会产生一 定频率的脉震转矩,脉震转速和脉震功率.此时,定 子的铜耗和转子的铁耗都有所增加,使电机温升增 加.并有可能损坏电机
异步电动机的平均电磁转矩与转速的变化关系 见图4
)/(N?In)
图4异步电动机的平均电磁转矩与转速的变化关系 Fig.4T-nchartofanasynchronousmotor
曲线a是异步电动机在没有自激情况下的平均 电磁转矩与转速的关系曲线:曲线b,C是异步电动 机在存在自激情况下的平均电磁转矩与转速的关系 曲线.假设异步电动机在没有串联电容的情况下正 常运行,工作在曲线a的1点上(转速为凡,电磁转 矩为T1)此时投入串联电容.如果其自激区是1
区,则异步电动机工作点1不在自激区内,它仍可正 常运行:如果其自激区是2区.则异步电动机工作点 1就在自激区内,异步电动机工作点立即转至工作 点2,而此时提供的电磁转矩变小,不能带动负载, 转速将下降,工作点将沿曲线C向下移,一直到能提 供足够大电磁转矩的新的平衡点(稳态自激工作 点).但图中曲线c上的工作点已不能提供足够大的 电磁转矩,电机将出现堵转现象,其运行电流将迅速 上升,从而可能损坏电机.即使存在新的平衡点,但 此时的转速降低,转差率s增大,其运行电流增大, 也可能会损坏电机.
异步电动机定子电阻r对自激区的关系可见图 5.其画出了两种不同电阻r时的自激区.根据此图 可以看出,电阻r增大时,自激区将缩小.在同一转 速下,定子电阻r越小,所对应的临界容抗越小. 同一电机在不同转速下所对应的临界容抗也有 自动化与仪表2006(5)
所不同,一般转速越高,所对应的临界容抗越大. 所以串联电容的容抗越小(即电容值越大),越不 容易产生自激现象.而为了完全避免自激,只有选择 非常大的电容,如图5中的但实际运用中很难 做到
(电容容抗)
二:__:f1y
图5异步电动机自激区随定子电阻变化的情况 Fig.5chanofanasynchronousmotorinself-excitation
3电容的选取
3.1电容选取条件
1)避免电机自激现象的电容选取条件
根据以上分析,在电机参数一定的情况下,电机 能否避免自激问题就取决于电容的选取.选取的电 容必须大于自激区的临界电容值,电容越大越不容 易产生自激问题这可作为选择条件1
文献『11给出了异步电动机自激区的算法,就可 算出自激区的临界电容值.图6是对应的异步电机 在频率为/Tt,转差率为几时的自激等值电路. -
jXJmrjmXIjmX2
]厂L—广
l[j
,m(jn);j棚
图6异步电机在频率为nl,转差率为,l时的自激等值电路 Fig.6Equivalentcircuitdiagramofanasynchronous
motorinse什一excitatiOnwhilef:,ands:,l
稳态自激的条件是图6中的总阻抗为零,所以 异步电机自激区的边界条件为
咖(1)
r=一mR(n)=一m(2)
田
其中:
17,=m—C
=—
x,-x
—
/
,
是转子的时间常数
(3)Tab.1
(4)
(5)
Xs=X慨,,厂一异步电动机转子开路时的定子电抗; Xr=X慨,,厂一异步电动机定子开路时的转子电抗; ——
异步电动机定子漏电抗:
厂异步电动机转子漏电抗;
,异步电动机励磁电抗:
一
电源频率;
,——异步电动机转速;
,00
异步电动机同步转速.
计算步骤如下:
a.给定值(应为一0之间的值);
b.计算出对应的r和的值;
C.凑出与电机的定子电阻r相接近的和 的值:
d?根据计算式c计算出临界电容值.
2)不影响稳态电流的电容选取条件
根据前面所述的卜一C串联电路分析,当 wL?—时,可以忽略电容c对稳态电流分量的" 影响,这可作为选择条件2.
根据条件l和条件2,就可选出能使异步电动 机正常运行的电容.在实际运用中.条件l比条件2 更为苛刻,所以一般只根据条件l来选取电容. 3.2实例
以一个空调压缩机电机为例.在三相电压 380V,频率50Hz的交流电源下,其电机参数为(单
位为Q)
1=3.2192=2.339Xm=81.75 r=2.772Rr=2.519
所以
=1+Xm=84.969Xr=X2+Xm----84.089
2
一5493To=Xr=33?382 根据以上数据和该电机的定子电阻.可选出/"t 取值应在一0.45到一0.4之间,所以电容应选取大于 22oouF以上
表1异步电机自激参数计算表
Parametersofall;ynch巾n0usm咖rinsolf~ 4电动机的起动问题
为了避免异步电动机在起动过程的自激区.串 '
j1一
联电容临界值为:=_{_,其中,仁.
(1一V),
仍以上例为例,电容值应选取19600uF以上.远大 于额定转速下的自激临界电容值.由以上分析可以 看出.除非串联电容选择得非常大.否则很难避免异 步电动机起动过程的自激区.所以异步电动机起动 过程中一般都要经过自激区.起动过程中也更容易 引起自激问题.图7是异步电动机的电磁转矩一转 速曲线和负载转矩一转速曲线相交的情况.若负载 特性为1=厂()时,电机将在l发生稳态自激:若 负载特性为=厂()时,因它与平均电磁转矩无交 点,虽然电机在起动过程中发生了稳态自激.但它会 冲过自激区而在额定转速正常运行.
/'t(转速)/
(r?min)
自激区
图7异步电动机的电磁转矩一转速曲线和负载转矩一转速 曲线相交的情况
Fig.7T-nchartofanasynchronousmotorinself-excitation
只要最终工作状态不在自激区内.就可以避免 异步电动机自激问题.为了解决异步电动机起动过 程中的自激问题,(下转第l9页)
尺位置上的红外光接收管接收不到红外光信号,而 使Ic1一i反相放大其输入端为低电平.促使Ie1一i输 出高电位,致使电子开关Ie2一i闭合,脉冲发生电路 发出每分钟个脉冲,送给计数驱动电路,推动电磁 计数器进行每分钟次计数来实现累加计量.准脉 冲产生器是由Ic3实现.它分别由25个电子开关 Ie2一n(n=l,25)分别提供的25个各不相同电位信 号,而产生25个不同的脉冲信号.计数驱动电路是 由BG1实现,它把基准脉冲产生器输出的脉冲信号 放大后,驱动电磁计数器计数,另外在输出端经RS一 485接口将信号远传给计算机,实现集中监控管理. 3装置特点
1)保留原有设施.增加计量功能——精巧. 2)拆分,嵌入组合式结构——方便.
3)气,电分离设计——安全.
4)计算机联网控制——科学.
5)抗干扰效果好——准确.
4技术指标及参数
1)测量精度?4%:
2)32作压力0.6Mpa:
3)使用温度(O,8O)?;
4)相对湿度80%:
5)流量范围(1,10)L/min;
6)电源电压DC12V:
7)接口RS一485.
5结语
可拆装嵌入式吸氧计量装置是应医院医疗环境
需求进行创新,开发研制的.该装置适用于各种液体
和气体浮子的流量计量.本吸氧计量装置已获国家
专利.在此基础上又研发了以单片机取代数字电路
的第二代吸氧计量装置,在搞好社会服务的基础上
也会创造出很好的经济效益.
参考文献:
[1】伏春干.医用供氧技术[M】.北京:化学工业出版社,2004. [2】赵负图.光电检测控制电路手册[M】.北京:化学工业出版社, 2oo1.
[3]陈永浦.新编555集成电路应用800例[M].北京:电子工业出版 社.2000.
[4】徐建平,都明生,黄咏委,仪本安.防爆技术[M】.北京:机械工业出 版社.2002.
[5】罗初东,凌耀基,谢国贤,吴志恩.现代实用电子计术手册[M】.广 州:广东科技出版社.1990.
本吸氧计量装置国家专利号:【012644390】
?
<>?<>?<>?<:>?<:>?<>?<>?<>?<>?<>?<>?<>?<>?<>?0?0?0?0?0?0?0?0?0?0?0?0?0?0?0?0?0?0?0?0?0?0?0?0?0?0?0?0?0?0?0?
(上接第16页)可以设计在电机起动过程中使串 联电容不工作,等电机完成起动过程稳定运行后.再 将串联电容投入使用,见图8.在电机起动前,先闭 合接触器KM2,短路串联电容,再闭合接触器KM1, 使电机起动.等到电机起动完成稳定运行后,再断开 接触器KM2,使串联电容投入工作.
KM1电容C
图8起动原理图
Fig.8Startingcircuitdiagram 5结语
由以上分析可知:
自动化s仪表2006(5)
电机
1)避免电动机自激问题的电容选取原则是根据 电动机的参数和运行转速可估算出自激区的临界电 容值,选取的电容必须大于此临界电容值,电容越大 越不容易产生自激问题
2)异步电动机起动即使选取的电容大于自激区 的临界电容值(即最终工作状态不在自激区内),但 在电动机起动过程中仍有可能引起自激问题.可以 在电机起动过程中使串联电容不工作,等电机完成 起动过程稳定运行后,再将串联电容投入使用,从而 避免电动机起动过程中的自激问题.
参考文献:
[1】串联电容补偿研究小组.串联电容引起的电动机自激[M].北京:
科学出版社,1978.
[2】徐东辉,李志刚,管学理.电机温升自动测试装置[J】.实验技术与
管理,2000,(1):41.
[3】国家质量技术监督局.GB755—2ooO旋转电机额定和性能[M].北
京:中国标准出版社.2000.
I41邱关源.电路【M】.北京:高等教育出版社,1978.?
转载请注明出处范文大全网 » 判断三相电机绕组电路



 晓玖_
晓玖_

