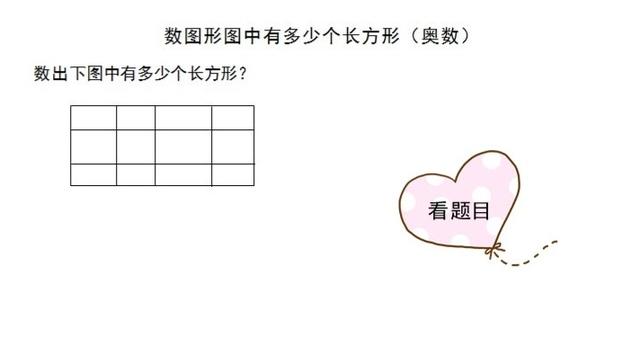
范文一：数出下图中有多少个长方形

数出下图中有多少个长方形, 【思路导航】数图中有多少个长方形和数三角形的方法一样，长方形是由长、宽两对线段围成，线段 CD上有3+2+1=6(条)线段，其中每一条与AC中一条线段对应，分别作为长方形的长和宽，这里共有6×1=6(个)长方形，而AC上共有2+1=3(条)线段也就有6×3=18(个)长方形。它的计算公式为: 长方形的总数=长边线段的总数×宽边线段的总数 (3+2+1)×(2+1)=18(个) 答:图中共有18个长方形

?BOD 2个;由3个基本角构成的角有:?AOD 1个。所以，图中一共有3+2+1=6(个)角。 练习2

:数出图中有几个角, (1) ( 2) 【例题3】数出右图中共有多少个三角形, 【思路导航】

方法一:我们可以采用按边分类数的方法。以PA为边的三角形有:?PAB、?PAC、?PAD、3个;以PB

为边的三角形还有:?PBC、?PBD 2个;以PC为边的三角形还有:?PCD 1个。所以，图中共有三角形3+2+1=6(个)。方法二:把图中三角形 ?PAB、?PBC、?PCD看做基本三角形来数，那么，由1个基本三角形构成的三角形有:?PAB、?PBC、?PCD 3个;由 2个基本三角形构成的三角形有: ?PAC、?PBD 2个;由3个基本三角形构成的三角形有:?PAD 1个。所以，图中一共有3+2+1=6(个)三角形。方法三:我们发现，要数出图中三角形的个数，只需数出线段 AD中包含几条线段就可以了，即3+2+1=6(个)。所以图中共有6个三角形。 练习3:数出图中共有多少个三角形, (1)

(2) 【例题4】数出下图中有多少个长方形, 【思路导航】数图中有多少个长方形和数三角形的方法一样，长方形是由长、宽两对线段围成，线段 CD上有3+2+1=6(条)线段，其中每一条与AC中一条线段对应，分别作为长方形的长和宽，这里共有6×1=6(个)长方形，而AC上共有2+1=3(条)线段也就有6×3=18(个)长方形。它的计算公式为: 长方形的总数=长边线段的总数×宽边线段的总数 (3+2+1)×(2+1)=18(个) 答:图中共有18个长方形。 练习4: (1)数出下图中有多少个长方形, (2)数出下图中有多少个正方形, OC B A P D C B A F E D CBA K GIHGF E D CBA D C B A

知识要点 爸爸给晶晶出了一道题:“小朋友们在路的一边植树，先植一棵树，以后每隔3米植一棵，已经植了9棵，问第一棵和第九棵树相距多少米,”晶晶一看，随口答题:“27米。”同学们，晶晶答对了吗, 这一类应用题我们通常称为“植树问题”。解答这类问题的关键是要弄清总距离、间隔长和棵数三者之间的关系。解答植树问题先要考虑植树的方式，一般在不封闭的线路上植树，棵数,总距离?间隔长，1;在封闭的线路上植树，棵数,总距离?间隔长。 另外，生活中还有一些问题，可以用植树问题的方法来解答。比如锯木头、爬楼梯问题等等，这时解题的关键是要将题目中的条件和问题与植树问题中的“总距离”、“间隔长”、“棵数”对应起来。 二、精讲精练 【例题1】小朋友们在路的一边植树，先植一棵树，以后每隔3米植一棵，已经植了9棵，问第一棵和第九棵树相距多少米, 【思路导航】要得出正确的结果，我们可以画出如下的示意图: 根据“已经植了9棵”，从图中可以看出，第一棵树和第九棵树之间的间隔是9-1=8(个)，每个间隔是3米，所以第一棵和第九棵相距3×8=24(米)，具体列式如下: 3×(9-1) =3×8=24(米) 答:第一棵和第九棵树相距24米。 练习1: (1)在路的一侧插彩旗，每隔5米插一面，从起点到终点共插了20面，这条道路有多长, (2)在学校的走廊两边，每隔4米放一盆菊花，从起点到终点一共放了20盆，这条走廊长多少米, 【例题2】在一条长42米的大路两侧栽树，从起点到终点一共栽了14棵，已知相邻两棵树之间的距离都相等，问相邻两棵

树之间的距离是多少米, 【思路导航】根据“在路的两侧共栽了14棵树”这个条件，我们可以先求出每一侧栽了14?2=7(棵)树，那么从第1棵树到第7棵树之间的间隔是7-1=6(个)。42米长的大路平均分成6段，每段是42?6=7(米)。列式如下: 42?(14?2-1)=42?(7-1)=42?6 =7(米) 答:相邻两棵树之间的距离是7米。

03米6米9米12米15米18米21米24米9棵 8棵 7棵 6棵 5棵 4棵 3棵 2棵 1棵 练习2:在公园一条长30米的路的两侧放椅子，从起点到终点共放了12把椅子，相邻两把

把一根钢管锯成小段，椅子的距离相等，相邻两把椅子之间相距多少米, 【例题3】

一共花了28分钟，已知每锯开一段需要4分钟，这根钢管被锯成了多少段, 【思路导航】我们先求出钢管被锯开了28?4=7(处)，因而被锯开的段数有7+1=8(段)。列式如下: 28?4+1 =7+1 =8(段) 答:这根钢管被锯成了8段。 练习3: 一根圆木锯成2米长的小段，一共花了12分钟。已知每锯下一段要3分钟，这根圆木长多少米, 【例题4】甲、乙两人比赛爬楼梯，甲跑到4楼时，乙恰好跑到3楼，照这样计算，甲跑到16楼时，乙跑到了多少楼, 【思路导航】解答爬楼梯问题时，不能以楼层进行计算，而要用楼梯段数进行计算，因为第一层楼是不用爬的，“楼层数-1”才是要走的“楼梯段数”，根据题意“甲跑到4楼时，乙恰好跑到3楼”，实际上是说“甲跑3段楼梯与乙跑2段楼梯所用的时间相同。”照这样计算，甲跑到16楼，也就是跑了15段楼梯，应是甲跑3段楼梯所用的时间的5倍，在同一时间里，乙跑的楼梯段数也是他跑2段楼梯的5倍，也就是这时乙跑了10段楼梯，即他跑到了第10+1=11(楼)。列式如下: (3-1)×[(16-1)?(4-1)]+1 =2×5+1 =11(楼) 答:甲跑到16楼时，乙跑到了11楼。 练习4:小明和小红两人爬楼梯比赛，小明跑到第4层时，小红跑到第5层，照这样计算，当小明跑到第16层时，小红跑到了第几层, 【例题5】一个圆形跑道长300米，沿跑道周围每隔6米插一面红旗，每两面红旗中间插一面黄旗，跑道周围各插了多少面红旗和黄旗, 【思路导航】在圆周上插旗，插的面数正好等于分成的段数，所以插了红旗300?6=50(面)，由于每两面红旗中间插一面黄旗，所以黄旗的面数就等于红旗的面数，也是50面。 300?6=50(面) 答:跑道周围插了50面红旗和50面黄旗。

练习5: (1)有一个正方形水池，周长是200米。如果沿着水池周围每隔10米装一盏红灯，再在相邻的两盏红灯中间等距离地装4盏黄灯。问水池周围一共装了几盏红灯,几盏黄灯, (2)一条公路长480米，在两旁植树，两端都植。每隔12米植一棵樟树，两棵樟树中间又等距离地栽了3棵柳树。问樟树和柳树各栽了多少棵,

范文二：图中有多少个长方形解法

图中有多少个长方形,

趣味数学

图为一个由5行8列共40个小正方形组成的长方形，问这个图中有多少个长方(三年级奥数题) 形,

1.方形图形的数目

把正方形也看作是长方形，先算出所有方形图形的数目。 把上图按纵向分层，共有层数:5，4，3，2，1,15(纵向数线段) 每一层的图形为:8，7，6，5，4，3，2，1,36(横向数线段) 方形图形共有:36×15,540(个)

2.正方形的数目

由1×1的小正形组成的正方形为:5×8,40(个)

由2×2的小正形组成的正方形为:4×7,28(个)

由3×3的小正形组成的正方形为:3×6,18(个)

由4×4的小正形组成的正方形为:2×5,10(个)

由5×5的小正形组成的正方形为:1×4,4(个)

正方形共计:40，28，18，10，4,100(个)

3.长方形的数目

长方形的数目,方形图形的数目,正方形的数目,540,100,440(个)

推广:如果上图是一个由m行n列共mn个小正方形组成的长方形，那么这个

图中有多少个长方形,

假设m

1.方形图形的数目

把上图按纵向分层，共有层数:m，(m,1)，(m,2)，…，2，1,m(m，1)/2

(纵向数线段)

每一层的图形为:n，(n,1)，(n,2)，…，2，1,n(n，1)/2(横向数线段) 方形图形共有:m(m，1)/2×n(n，1)/2,mn(m，1)(n，1)/4(个) 2.正方形的数目

2由1×1的小正形组成的正方形为:mn,m(m，a),m，ma

2由2×2的小正形组成的正方形为:(m,1)(n,1),(m,1)，(m,1)a

2由3×3的小正形组成的正方形为:(m,2)(n,2),(m,2)，(m,2)a ……

2由(m,1)×(m,1)的小正形组成的正方形为:[m,(m,2)]×[n,(m,2)],2，2a

2由m×m的小正形组成的正方形为:[m,(m,1)]×[n,(m,1)],1，a 正方形共计:

22222[m，ma]，[(m,1)，(m,1)a]，[(m,2)，(m,2)a]，…，[2，2a]，[1，a]

22222,[m，(m,1)，(m,2)，…，2，1]，[m，(m,1)，(m,2)，…，2，1]a

,m(m，1)(2m，1)/6，m(m，1)a/2

,m(m，1)(2m，1)/6，m(m，1)(n,m)/2

3.长方形的数目

长方形的数目,方形图形的数目,正方形的数目

,mn(m，1)(n，1)/4,[m(m，1)(2m，1)/6，m(m，1)(n,m)/2] 有了上述一般性公式，再回过头来用一般求特殊就更容易了。 下面我们用这个“m行n列”的一般性公式来计算一下上例中“5行8列”的特殊情

况。

5×8的长方形的数目为:

mn(m，1)(n，1)/4,[m(m，1)(2m，1)/6，m(m，1)(n,m)/2] ,5×8×(5，1)(8，1)/4,[5×(5，1)(2×5，1)/6，5×(5，1)(8,5)/2] ,5×8×6×9?4,(5×6×11?6，5×6×3?2)

,540,(55+45)

,440

利用这个方法计算相当于求代数式的值，它免除了动脑筋的繁琐，确实很方便～

范文三：【数学逻辑】在棋盘格中有多少个长方形——定义、排序与分类

■ 吴宗敏（复旦大学长江学者、特聘教授）

在学生找我面试时，我经常出的题目是：一个国际象棋8×8的棋盘，问上面有多少个长方形。有的学生很聪敏，马上回答9条直线里面选2条的组合的平方。这就涉及长方形的定义：“两对互相垂直的平行线构成一个长方形”。有了这个通俗、明确、严格的定义，导出这样的漂亮的计算公式就非常自然了。当然对这样的学生，我会说正方形不算长方形。因为我关心的不是问题的答案，而是你考虑、分析、解决问题的思想与步骤。

首先应该是长方形的定义。在我还没有说出这个长方形定义时，你是怎么定义长方形的？

有的学生会在给出题目时立即问我，正方形算不算长方形？很好，你已经注意到了在这个题目中长方形定义的重要性。如果这是高考的题目，你会说这个题目的条件有歧义，因为你害怕与标准答案不符，你不知道出题人有没有把正方形算成长方形。说实话，我不太喜欢这样的学生，他们只关心这次考试可以得到多少分。你注意到了条件有歧义当然是好事，但你不能把问题退回去。你就应该对不同的歧义给出不同的答案。在实际问题中，你是碰不到高考类的题目的。高考类题目，条件通常是充分且必要的，如果解了半天题目中有的条件一直没用到，你就会怀疑解法有问题；解一定是存在且简洁的，如果出现小数以后的4位，你就会怀疑是不是算错了。而绝大多数实际问题，条件是模糊的，也就说，哪些可以作为条件，哪些不可以作为条件，是需要你自己去整理、发掘的，甚至解的存在性都是需要证明的，答案可能也不是简洁的，明确的、唯一的。

回到原来的题目，在中学里老师教我们的第一步是审题，也就是定义。你先要理清题目中的什么是什么。任何科学问题，第一步都是要审题，通常就是问题中那些名词的定义以及这些名词间的关系。数学类的研究论文通常都是从定义及假设开始的。

对于我们的题目，我通常要求学生假想自己是一个幼儿园的老师，要教给幼儿园的孩子解这么样的题目。你要把问题分成一小步一小步的，幼儿园孩子能够理解的。这时长方形的定义可能只能举例说明了。小孩子也没有学过排列组合，就是要找到一种科学的数数的步骤，可以不犯错地,把长方形的个数数清楚。

有了长方形定义、说明或者只是理解后，就要开始数了，怎么数呢？数数就是排序，要对所有的棋盘里的长方形进行排序，让它们与自然数做一一对应。因为长方形有各种形状的，有各种位置的，好像一个一个地数清楚也并不容易。对待科学问题，一个大问题不会做，那就要分解成一些小问题，也就是要对长方形进行分类。一种类型一种类型地数。在中学时老师已经教过。分类应该是一个完全的分类，要求每个元素属于一类，且只属于一类，每类有明确的特性特征说明。这样你才可以一类一类地，然后对类中的一个一个的长方形进行数数或者排序。首先是类的排序，有的学生会以面积分类。面积分类是容易排序的，但是某种面积（如11）是否一定有长方形也是一个问题，以面积排序会缺了一些类，要搞清缺了哪些类，又有一番周折。同一面积的长方形也可以有不同的形状，譬如2×2与1×4。这样同类中的元素也不容易排序。这给以后数这一类型的长方形带来困难。好像不是一个好的分类。

对于这个问题，可能用长方形的长乘以宽j×k分类较好。找到好的分类方法是每个领导必须学会的领导艺术。这样你才可以把一个大问题分解成一些小问题，分配给不同的下级部门去做。这也是计算机并行算法的核心所在。长乘以宽j×k同时也是这类长方形的特性说明，而且还可以排序，那叫做字典排列法。把j小的排在前面，当j相等时，再用k决定前后。这样的分类还有一个好处，就是类中的元素也可以用他的左下角的坐标进行字典排列，这样的序还是一个全序，不会跳过或漏数某种长方形，不会跳过或漏数某个长方形。有了这些思想以后，幼儿园的小孩就会数出棋盘中有多少个长方形了，而且你换成一个更大的棋盘，他也会数出来了。如果那个小朋友更加聪明一些，有些领导天赋，他还可以将不同的类交给不同的其他小朋友去数，当然他自己要学会加法，能够总结或者集成其他小朋友的计算结果。一个系统工程就可以这样地用并行算法完成了。

* 该文将收录在即将由复旦大学出版社出版的《数学之外与数学之内》中，原载于数学英才（微信公众号：shuxueyingcai）。

范文四：有一个长方形

有一个长方形,它的长是宽的4倍,对角线长17cm求这个9. 如图,?ABC中,3AH=AB,AE=EF=FC,BD=DC,求四长方形的面积。边形DHEF占?ABC面积的几分之几?

2. 直角?ABC中,AB=6cm,BC=8cm,AC=10cm,现将三角形10. 兄弟两人骑马进城,全程50千米。马每时行10千米. 折叠，使A与C重合，EF=?cm, 但马只能一个人骑。哥哥每时步行5千米,弟弟每时

步行4千米。两人轮换骑马和步行,骑马者走过一段

路就下鞍拴马,然后步行。而步行者到达此地，再上

马前进。他们早晨6点动身,何时能同时到达城里?

3. 图中三角形都是直角三角形，四边形都是正方形，

所有正方形的面积和是980平方厘米，求最大正方形

的边长,

11. 甲乙丙三辆车同时从A地出发去B地, 甲车每分走

1000米,乙车每分走800米，出发后6分甲车超过

了一名长跑运动员,2分后乙车也超过去了,又过了

2分丙车也超了过去,丙车每分钟走多少米?

4. 下图中?ABC和?DEF是两个完全相同的等腰直角三

角形,AB=9cm, FC=3cm,求五边形PGFBH的面积.

12. 某人沿着电车道旁的便道以4.5千米/时的速度步

行,每0.12时有一辆电车迎面开过,每0.2时有一辆

电车从后面追过。如果电车按相等的时间间隔以同

5. 如图，直角三角形的直角边分别是4和8，图中3个正一速度不停地往返而行,那么电车的速度是多少?电

方形的面积和比4个三角形面积和大多少? 车之间的时间间隔是多少?

6. 如图,长方形中,长和宽分别是8cm和4cm, S?HBF与 213. *甲乙二人从相距37.5千米的两地相向而行。若甲先S?DEP的面积和是10cm,求四边形ABCD的面积. 出发2时,则在乙动身2.5时后两人相遇;若乙先出发

2时,则甲动身3时后两人相遇。求甲、乙二人的速度?

27. 如图,两个正方形，DB=4cm,求S?ABC=?cm,

14. 甲乙二人在操场的400米跑道上练习竞走,两人同

时出发,出发时甲在乙后面,出发后6分钟甲第一次

超过乙,26分钟后第二次超过乙。假设两人的速度 保持不变,问:出发时甲在乙后面多少米? 8. 矩形ABCD=48cm2,AE=EB,BF=2FC,DH=2HF, S?

EHF=?

你好，因为三月份 “希望杯，走进美丽数学花园”竞赛， 后面不停课，下周六7:20,9:20，要我这集体报名请

带报名费。希望杯8元，走美15元，英语竞赛15元，可选

择报名，(在我这没有交费，也就是不打算继续上课的

请不过来)也可以自己报名，电话83207321谢谢

范文五：35块瓷砖里有多少正方形瓷砖和多少长方形瓷砖

35块瓷砖里有多少正方形瓷砖和多少长方形瓷砖？

35÷2=17（组）……1（块） 余下的1块为正方形瓷砖。

正方形：1×17+1=18（块）

长方形：1×17=17（块）

4、第4题

5、第5题：

明确：信号灯亮的顺序依次是红灯、绿灯、黄灯；从10时到10时15分，信号灯一共亮了42次。

每3个为一组，每组中有一个红灯，一个绿灯和一个黄灯。

42÷3=14（组）

所以红灯、绿灯和黄灯各亮了14次。

6、第6题

提示：通常把7天看作一组，11月份共有30天。

每7天为一组，每组中为2天休息、5天工作。

30÷7=4（组）……2（天） 余下的2天为休息日。

休息：2×4+2=10（天）

工作：5×4=20（天）

7、第7题：

今天你有什么收获呢？

转载请注明出处范文大全网 » 数出下图中有多少个长方形