范文一:幂函数的教学设计
幂函数的教学设计
刘 飚 (江苏省张家港市暨阳高级中学 215600)
新课标指出高中数学课程应该返璞归真, 努力揭示数学概念、法则、结论的发展过程和本质. 通过典型例子的分析和学生自主探索活动, 使学生理解数学概念、结论逐步形成的过程, 体会蕴涵在其中的思想方法, 追寻数学发展的历史足迹, 把数学的学术形态转化为学生易于接受的教育形态. 遵循这一理念笔者尝试幂函数的教学设计与大家交流.
习, 使学生加深对函数的理解. 重要的是, 这段内容还蕴涵着归纳类比、数形结合、从特殊到一般, 从一般到特殊等重要的数学思想和数学方法.
?教学目标
(1) 了解幂函数的概念, 了解几个具体幂函数图象的变化情况和性质.
(2) 在数学实验平台上, 能自主探究, 经历幂函数图象和性质探索发现的过程, 提高观察、归纳、概括能力. 学会借助于数学软件等工具研究、探索和解决问题.
(3) 体会特殊到一般、数形结合、分类讨论等数学思想方法, 培养学生积极参与、合作交流的主体意识, 使学生感受数学学习的意义, 改善学生的数学学习信念(态度、兴趣等) .
?教材重点和难点处理思路
重点:幂函数的概念和常见性质.
难点:经历数学实验方法探索研究幂函数的性质, 学会数学地解决问题.
为了突出重点、突破难点, 在教学中采取了以下策略:
(1) 创设情境, 激发学生学习兴趣, 从学生已有知识出发, 设计一些适合学生学力的数学实验平台, 分层次逐步引导学生观察图象与幂函数解析式中 取值的关系, 抽象、归纳出幂函数的性质和幂指数的关系, 从而真正认识解析式形式化的特点. (2) 数学实验采取小组合作研究共同完成的形式, 通过学生的自主探究、合作交流, 从而实现对幂函数的性质和幂指数的关系知识的建构.
1 设计思想
实际教学中, 我们发现如果学生不经受足够的亲身体验而简单地记住结论的话, 往往很难掌握幂函数的性质和幂指数的关系, 因此在教学中这段内容不以采取简单的 告诉 方式, 而是让学生自主发现命题、发现规律, 让他们 知其然, 更要知其所以然. 又让学生初步学会如何应用规律解决问题, 体会知识的价值, 增强求知欲.
2 学情分析
本节课授课的对象是高一年级的学生, 他们对函数的概念及性质已经有了一定的认识, 基本上掌握了研究函数性质的一般方法. 这节课是学生在学习了指数函数、对数函数的基础上, 研究的
第三种函数. 由于刚从初中升入高一, 学生仍保留着初中生的许多学习特点, 能力发展正处于形象思维向抽象思维转折阶段, 通过学习幂函数知识, 既可以体验类比研究的过程, 又能通过对幂函数的学习重温研究函数的一般思想方法, 从而掌握研究函数的一般方法.
3 教材分析
幂函数是新课标教材新增的内容, 位于必修1第二章基本初等函数(! ) 的第四节. 新教材将幂函数的位置放到了指数函数与对数函数之后, 并且将幂函数研究的对象限定为几个具体函数, 本节课主要内容为通过实例引出幂函数的概念, 使学生了解幂函数的模型, 了解幂函数与指数函数的区别. 通过一些特殊的幂函数的图象, 观察总结出幂函数的变化情况与性质, 培养学生的抽象概括能力. 通过对幂函数的研究, 结合一次函数、4 教学过程设计
4 1 问题情境
由 神六升空 引入研究天体运动, 研究太阳系八大行星.
#设计意图?兴趣是最好的老师. 如果一节课有良好的开头, 那就意味着成功的一半. 因此选择从学生感兴趣的问题引入, 激发学生思维, 激发学生的求知欲.
表1中给出了八大行星离太阳的距离和它们.
表1
距离/106km 周期/d
水星57. 988
金星108. 2225
地球149. 6365
火星227. 9687
木星778. 34329
土星142710753
天王星287030660
海王星449760150
在Ex cel 工作表中输入上述数据, 作出散点图后观察散点趋势, 尝试用指数、对数、乘幂和二次多项式拟合. 与指数、对数、二次多项式比较用乘幂拟合得到的R 值为1, 因此用乘幂进行拟合最恰当. 再进行观察发现, 运行周期T 与d 满足关系T &0. 2001d &0. 2d 2.
这就是开普勒第三定律的数学表达式, 它揭示了 公转时间的平方与平均距离的立方成正比 这一天体运动定律.
#设计意图?力求通过信息技术与课程内容的整合, 激发学生对学习的兴趣. 通过开普勒第三定律发现所用时间与利用Ex cel 探求所用时间对比, 体会现代技术的力量. 鼓励学生, 把现代技术作为学习研究和探索解决问题的工具. 4 2 建构数学
通过学生观察、对比, 发现y =x 2, 这是一个区别于指数、对数、二次多项式的函数, 我们把这样的函数定义为幂函数.
定义:一般地, 我们把形如y =x 的函数称为幂函数, 其中x 是自变量, 是常数.
#设计意图?通过与指数函数、对数函数定义的类比, 得出幂函数定义.
思考1 判断下列函数中哪些是幂函数:y =x -2, y =2x 2, y =2, y =(x -1) 2, y =() x . 2
问题1 幂函数与指数函数有什么区别与联系?(组织学生回顾指数函数的概念, 明确二者的区别, 得出如下结论. )
结论:幂函数和指数函数是我们高中数学中研究的两类基本初等函数, 从它们的解析式来看有如下区别:对幂函数来说, 底数是自变量, 指数是常数; 对指数函数来说, 指数是自变量, 底数是常数.
#设计意图?通过与指数函数、对数函数对比, 加深学生对幂函数定义和呈现形式的理解. 4 3 数学运用
问题2 我们已经对幂函数的概念有了一定的认识, 能否举一些幂函数的例子?
3
根据我们前面学习指数函数、对数函数的学习经历, 我们下面应该研究它们的图象和性质.
问题3 我们应怎样研究幂函数?
例如:y =x , 用Excel 描点画出x ?0时函数的图象(在作出x ?0部分图象后可进一步提问)
问题4 用Ex cel 描点画出x ?0时函数的图象后, 能否不用描点法作出x <0时函数的图象?>
#设计意图?引导学生认识到对于幂函数可以先利用解析式研究函数的奇偶性, 然后再研究图象、单调性等性质.
思考2 写出下列函数的定义域, 并指出它们的奇偶性:(1) y =x ; (2) y =x ; (3) y =x .
根据幂函数的解析式及奇偶性, 我们主要研究幂函数在第一象限的图象与性质.
问题5 幂函数在第一象限的图象与性质. 在这个环节中引导学生自由选择不同的幂函数, 利用几何画板中的函数的作图工具作图, 通过作图, 探究它们的图象与性质, 并将自己的探究结果记录下来. 在研究过程中, 学生会选择幂指数不同的多个幂函数进行研究, 分别记录它们的图象与性质, 并在探究过程中对幂指数的作用进行了初步的探索. (老师可根据实际情况对学生小组进行指导)
#设计意图?发现性质、弄清性质的来龙去脉, 是为了更好揭示幂函数的本质属性, 传统教学往往让学生在解题中领悟. 为了扭转这种方式, 可以引导学生回顾指数函数、对数函数的性质, 再利用类比的思想, 小组合作的形式通过图象主动探索出幂函数的性质.
对学生进行数学思想方法的有机渗透. (从特殊到一般再从一般到特殊、数形结合、分类讨论等) 考虑到各组的水平可能有所不同, 教师应巡视, 对个别组可做适当的指导.
组织小组交流幂函数在第一象限的图象与性质. 在这一环节中教师引导学生将幂函数在第一象限不同形态的图象画出来(图1) , 并请一名学生将图象画到黑板上, 通过对学生所画图象的纠错与分析和学生共同归纳出幂函数在第一象限的3
23
1. 4996
-2
文理科学生数学学习习惯差异的调查研究
刘文良 (江苏省新沂市教育局教研室 221400) 胡慧玲 袁亚洲 (江苏省新沂市高流中学 221411)
1 研究方法
采用抽样问卷调查法, 从我校高二年级选修物理的4个班中抽取2个班级共134人, 从高二年级选修历史4个班中抽取2个班级共130人参与调查. 问卷共有13个问题, 包括预习的时间、习惯、独立思考品质、独立完成数学作业的习惯、解题后反思的习惯和品质、数学爱好层次的品质、数形转化的习惯、处理难题的态度、听课认真程度、复习的习惯和考试期间复习习惯的品质等. 问卷
见附录.
2 调查结果及分析
发放问卷264份, 收回问卷264份.
(1) 独立思考与解题反思这两种思维品质的比较
在调查中, 独立思考的思维品质选 优 的理科占18. 67%, 文科占5. 38%, 选 良 的理科占56. 72%, 文科占59. 23%, 选 一般 的理科占24. 63%, 文科占35. 38%;
解题反思思维品质中
(1) 图象必过(1, 1) 点.
(2) 当 >1时, 过(0, 0) 点, 且y 随x 的增大而增大, 函数图象向y 轴方向延伸, 图象是下凸的. 在第一象限是增函数.
(3) 当0<><>
随x 的增大, 函数图象向x 轴方向延伸, 函数图象是上凸的. 在第一象限是增函数.
(4) 当 <0时, 随x="" 的增大,="" 函数图象与x="" 轴无限接近,="" 但永不相交.="">
(5) =1和 =0的情况略.
#设计意图?通过小组交流, 教师的引导, 提供一定的研究学习与情感交流的时空, 培养学生合作学习的能力; 突出学生学习的主体性, 能激发学生学习的兴趣.
思考3 不借助计算机你能画出函数y =x 的图象吗?
思考4 已知幂函数y =x
m -3
4 4 回顾小结
幂函数的概念, 几个简单的幂函数的图象, 幂函数图象的变化情况和性质. 4 5 作业布置、课后自评
(1) 必做题:教材第73页习题2. 4第1, 2, 4题; (2) 选做题:略.
图1
#设计意图?针对不同学习水平的学生, 选择不同的课外作业, 进行分层教学.
5 教学后记
本节课的设计一方面重视学生数学学习过程是活动的过程, 因此不是按照已形式化了的现成的数学规则去操作数学, 而是采取数学实验的方式, 使学生有机会经受足够的亲身体验, 亲历知识的自主建构过程; 使学生学会从具体情境中提取适当的概念, 从观察到的实例中进行概括, 进行合理的数学猜想与数学验证, 并作更高层次的数学概括与抽象, 从而学会数学地思考.
另一方面, 注重创设机会使学生看到数学的全貌, 体会数学的全过程. 整堂课的设计围绕研究幂函数的图象展开, 以问题 研究幂函数性质 为主线, 既让学生清楚如何研究函数, 明确学习目标, 又让学生初步学会如何应用规律解决问题, 体会知识的价值, 增强求知欲. 使传授知识与培养能力融为一体, 在转变学习方式的同时学会数学地思考.
(-3
m (Z ) 的图象与x 轴、y 轴都无公共点, 且关于y 轴对称, 求该函数的解析式, 并写出相应函数的定义域、值域、奇偶性、单调性.
#设计意图?利用练习巩固新知识, 加深理解.
范文二:微课《幂函数的概念》教学设计
微课教学设计
授课教师:柳荷红 微课名称:幂函数的概念
教学目标:
通过实例,理解幂函数的概念;能区分指数函数与幂函数;会用待定系数法求幂函数的解析式。
教学重难点:
重点 从五个具体幂函数中认识幂函数的一些特征. 难点 指数函数与幂函数的区别和幂函数解析式的求解.
教学方法与手段:
1.采用师生互动的方式,在教师的引导下,学生通过思考、交流、讨论,理解幂函数的定义,体验自主探索、合作交流的学习方式,充分发挥学生的积极性与主动性.
2.利用投影仪及计算机辅助教学.
教学过程:
函数的完美追求:对于式子N?a,
1. 如果a一定,N随b的变化而变化,我们建立了指数函数y?ax; 2. 如果a一定,b随N的变化而变化,我们建立了对数函数y?logax. 设想:如果b一定,N随a的变化而变化,是不是也应该确定一个函数呢? 创设情境
请大家看以下问题:
b
思考:以上问题中的函数y?x,y?x,y?x,y?x,y?x?1有什么共同特征? 引导学生分析归纳概括得出:(1)都是以自变量 x为底数;(2)指数为常数;(3)自变量x前的系数为1;(4)只有一项.上述问题中涉及的函数,都是形如y?x的函数. 探究新知
一、幂函数的定义
一般地,形如y?x(??R)的函数称为幂函数,其中x是自变量,?是常数.
?
?
2
3
2
y?x?中x?前面的系数是1,后面没有其它项.
小试牛刀
判断下列函数是否为幂函数:
1223
(1) y?x,(2)y?2,(3)y??x,(4)y?x2,(5)y?(?2x),(6)y?x?2.
x
4
1
思考:幂函数y?x?与指数函数y?ax有什么区别? 二、幂函数与指数函数的对比
结论:判断一个函数是幂函数还是指数函数的关键点是看自变量x是指数还是底数,如自变量x是指数,就是指数函数;如自变量x是底数,就是幂函数函数. 快速反应
下列函数中哪些是指数函数,哪些是幂函数:
(1)y?0.2x,(2)y?x,(3)y?3?x,(4)y?x.
(1)指数函数,(2)幂函数,(3)指数函数,(4)幂函数. 随堂练习
已知幂函数y?f(x)的图像经过点(2,2),试求这个函数的解析式 .
分析:因为所求的函数为幂函数,所以可用待定系数法,先设y?f(x)?x,再由已知条件解出?即可.
解:设所求的幂函数为y?x,
?
15
?
?函数的图像经过点(2,2), ?2?2?,即2?2?,
???
1 2
12
12
?所求的幂函数为y?x.
课堂小结
一、幂函数的定义;二、幂函数与指数函数的区别;三、待定系数法. 布置作业 随堂检测
范文三:简单的幂函数(教学设计)
§5 简单的幂函数(第1课时)
交大二附中 刘正伟
一、课标三维目标:
1.知识技能:了解简单幂函数的概念;通过具体实例了解幂函数的图象和性质,
并能进行初步的应用.
2.过程与方法:通过作函数图像,让学生体会幂函数图像的特点,会利用定义证
明简单函数的奇偶性,了解利用奇偶性画函数图像和研究函数的方
法。
3.情感、态度、价值观:进一步渗透数形结合与类比的思想方法;培养从特殊归
纳出一般的意识,体会幂函数的变化规律及蕴含其中的对
称性。
二、教学重点与难点:
重点:幂函数的概念,函数奇、偶性的概念。
难点:判断函数的奇偶性。
三、学法指导:
通过数形结合,类比、观察、思考、交流、讨论,理解幂函数的概念和函数的奇
偶性。
四、教学方法:
对奇偶性要求不高,题目不需要过难,尽量用多媒体和计算机画函数的图像,重
在从图上看出图像关于谁对称,着重从对称的角度应用这一性质,培养学生自己归纳总结的能力。
五、教学过程:
(一)创设情境(生活实例中抽象出几个数学模型)
1. 如果张红购买每千克1元的蔬菜x 千克, 那么她需要付的钱数
p=x元, 这里p 是s 的函数.
2. 如果正方形的边长为a, 那么正方形的面积S=a2, 这里S 是a 的函数.
3. 如果正方体的边长为a, 那么正方体的体积V=a3, 这里V 是a 的函数
4. 如果正方形场地的面积为S, 那么正方形的边长a=S1/2, 这里a 是S 的函数.
5. 如果某人t s内骑车行进了1km, 那么他骑车的平均速度
v=t-1km/s,这里v 是t 的函数.
【思考】上述函数解析式有什么形式特征?具有什么共同点?(教师将解析式写成指数幂形式,以启发学生归纳,板书课题并归纳幂函数的定义。)
(二)探究幂函数的概念、图象和性质
1.幂函数的定义
如果一个函数,底数是自变量x ,指数是常量α ,即y = x ,这样的函数称为幂函数.如α
【练】为了加深对定义的理解,让学生判别下列函数中有几个幂函数?
212x 2(1)y=x +x (2)y=(3)y=2 (4)y=2 (5)y=2x (6)y=x 3x x 2
2. 幂函数的图象和性质
【1】通过几何画板演示让学生认识到,幂函数的图象因a 的不同而形状各异
【2】引导学生从5个具体幂函数的图象入手,研究幂函数的性质
① 画出y =x , y =x , y =x , y =x , y =x -1的图象(重点画y=x3和
y=x1/2的图象----学生画,再用几何画板演示) 2312
学生活动:1. 学生自己说出作图步骤,交流讨论单调性。
学生活动:2. 观察交流,分析图像还有那些特点?
3. 观察函数值和自变量取值有什么特点?
我们还可以看到, f (x)=x3 的图像关于原点对称.并且对任意的x , f(-x)=(-x)3= -x3,即f(-x)= -f(x).
(三)奇函数、偶函数的定义
一般地,图像关于原点对称的函数叫作奇函数, 即f(-x)=-f(x);反之,满足f(-x)=-f(x)的函数y=f(x)一定是奇函数。
2学生通过类比,自己找出偶函数的定义,可以建议利用y=x
的图像特征?
一定是偶函数。
当函数f(x)是奇函数或偶函数时,称函数具有奇偶性。
例1:画出下列函数的图像,判断奇偶性.
(1)f (x)=-3x-1 ; (2) f (x)= x2 ,x ∈﹙-3,3〕
(3) f (x)= x2 -3 ; (4)f (x)= 2(x+1)2+1 图像关于y 轴对称的函数叫作偶函数,即f(-x)=f(x);反之,满足f(-x)=f(x)的函数y=f(x)
学生活动:思考讨论:
1. 总结奇偶性对函数定义域的要求.
2. 总结利用图像法判断函数奇偶性
(四)根据定义法判断奇偶性
例2.判断f (x)= -2x5 和g(x)= x4 +2的奇偶性.
由于从图像上进行观察是一种常用而又较为粗略的方法,严格的说,它需要根据奇
偶函数的定义进行证明。
学生自己先动手证明,教师一旁指导。要注意书写规范,并讨论交流定义法证明的步骤。
例3学生活动:动手实践
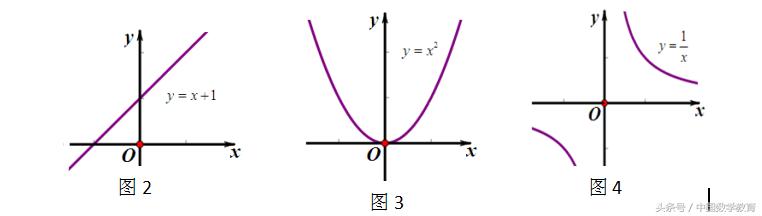
在图2-28 中,只画出了函数图象的一半,请你画出它们的另一半,并说出画法的
依据.
结论:
在研究函数时,如果知道其图像具有关于原点或y 轴对称的特点,那么我们可
以先研究它的一半,再利用对称性了解另一半,从而可以减少工作量.
六.归纳小结:(学生自己交流总结)
1 .本节课学习的主要知识是什么?
2. 如何确定函数的奇偶性,其定义域有何特征?
3.思考讨论填写常用幂函数规律表。
七.作业:课本第50页A 组1(2),2 , 3(1)(2), 4
选做:B 组 、第2题
八.板书设计:
简单的幂函数
α一. 定义:形如y = x,α是常量.
二. 奇、偶函数的定义:
三. 定义证明奇偶性。(教师板演)
八.教学反思:
范文四:《简单的幂函数》教学设计
《简单的幂函数》教学设计
【中图分类号】g633.6 【文献标识码】a 【文章编号】2095-3089(2012)12-0147-02
一、教学内容分析
本节课是《普通高中课程标准实验教科书·数学(1)》(北师大版)
第二章第五节《简单的幂函数》。本节内容为一课时,主要是一节数学概念课,介绍了幂函数的概念,并从几个幂函数的图像的对称性引出了奇偶函数的概念。由于函数的奇偶性是函数的又一重要性质,且幂函数是初等函数的一种,所以本节内容在《函数》一章占比较重要的地位。
二、学生学习情况分析
幂函数是在学生系统学习了函数概念,基本掌握了函数的单调性的基础上进行研究的。学生在初中已经学习过一次函数、二次函数、反比例函数,那么幂函数是六种初等函数的一种。其实一些简单的幂函数学生已经很熟悉,所以本节课引入很自然,但是通过一些幂函数图像的对称性,引入奇偶函数的概念,学生会有些的困难,特别是要学生找到判断函数奇偶性的方法更是困难的。
三、设计思想
学生是教学的主体, 本节课要给学生提供各种参与机会.为了调动学生学习的积极性,使学生化被动为主动。本节课我利用多媒体辅助教学, 教学中我引导学生从初中学过的函数出发,认识幂函数,体会引入奇偶函数的定义.在教学重难点上,我步步设问、启发学
范文五:幂函数的教学过程设计
第16卷第1期
2002年3月商洛师范专科学校学报V01.16CoⅡegeNo.1Jo啪alofShan出uoTeachersMar.2002
幂函数的教学过程设计
庞‘洪涛
(商州师范学校,陕西商州726000)
摘要:从幂函数y≈“的指数n2}的取值作为切入点,讨论了p、9取不同值时,幂函数
文献标识码:A文章编号:1008—3030f2002)01一0069—02定义域、值域、图象、性质及内在联系,从而掌握幂函数性质.关键词:幂函数;幂函数图象;性质;教学过程设计中图分类号:0122.6
幂函数是初等数学里的一种重要函数.它的定义是函数),=矿叫幂函数,其中戈是自变量,n是常数(n是实数,但在初等数学里只研究n是有理数的情况,所以本文只按n=旦_谈,p、g是互质整数).其定
p
义域、值域、图象的形状和位置关系比较复杂,不比前面学习的一次函数、二次函数和后面学习的指数
旦.
函数和对数函数那样定型.因此教学时宜通过具体例子分析、比较、观察,以帮助学生寻找),≈9随P、g取值不同时,其定义域、值域、图象的变化规律,突破难点.
1幂函数定义域和值域的教学设计
幂函数的定义域和值域是与n=旦一的取值密切相关的.教学时应充分利用学生前面学习过的整数
p
指数幂和分数指数幂的相关知识,以帮助学生总结规律.具体作法是首先给出函数
l1ll2
产茁,产石,产石‘,),:茁。,产菇膨f,芦丁,膨2,膨3,严~,),≈~,),:f丁,严~,芦。),≈),=z,产茁,y≈”,,
让学生根据以前所学知识,求出函数定义域和值域,然后引导学生得出结论(见后表).
2幂函数的图象和性质的教学设计
幂函数的主要性质是在观察幂函数图象的基础上得到的,因此如何较快速准确地画出幂函数的图象是教学重点.由于教材是在学习了函数单调性、奇偶性和反函数的内容之后安排学习幂函数的.所以,在教学时,应注意引导学生用这些知识来分析判断幂函数图象的形状和位置,使学生在画图前对幂函数的形状心中有“图”.
2.1幂函数图象的分布范围
旦-旦-
因为茹>0时,黟’>O,所以函数),剐9的图象不能在第四象限,又由于不论旦_取何值时,当z>OP
旦-旦_
时,产菇9都有定义,所以幂函数产菇9在第一象限都有图象.(在其它象限的图象可根据奇偶性得出)2.2幂函数的奇偶性
r旦I
1。p是奇数{9是奇数声:是奇函数,图象在一、三象限关于原点对称,
20【9是偶数严’是偶函数,图象在二、四象限关于y轴对称;p是偶数黟9是非奇非偶函数,图象只在第一象限.
收稿日期:2001-06—17作者简介:庞洪涛(1962一),男,陕西商南人,商州师范学校讲师
第2期谢谦:关于等倾干涉的讨论73对应组光束形成的下涉条纹亦对应重合.这表明两套T:涉是重合的。
结沦:光源的大小对等倾干涉条纹的可见度并无影响.
1。由于s和s7是扩展光源上的任意两点,构成扩展光源的所有点光源都给出自已的.套等倾r涉圆环,而且彼此重合,没有位移.
20因s,s7为非相干光源,焦平面上总强度是不同点形成的干涉条纹亮度之和,条纹的强度会大大增强,使干涉花样更加明亮,所以在观察等倾干涉条纹采用扩展光源是有利无害的.
至于等倾干涉条纹的特点,课本上叙述得很清楚,此处不再赘述.
对课本上的内容作以上改进后,学生普遍反映良好,取得了较好的教学效果.
参考文献
【1]梁绍荣主编.普通物理学?光学【M].北京:高等教育出版社,1993.
【2]姚启钧原著.光学教程[M].北京:高等教育出版社,1993.
DiscussiononInterferenceofEqualInterference
XIEQian
(PhysicsDepatnnent,ShangluoTeachersCoUege,Shangzhou,Shaanxi,726000)
Abstranct:Thispapermainlyusesasjmilarjnductjonmethodtodjscuss£hejnterference“equalinclinationofVariousl培htsources.Andatthesametimeitpmperly“estimate”theangleoftiltof1ightdu^ngthediscussionandthusmakesthetrainofthoughtclearandweUorganized.Asaresult,I.eaderscanunder言胁dinterfbrenceofequalinclinationmucheasilyandpletely.KeyWords:inte彘renceofequalinclination;opticalpath;angleoftilt;intemrence抽nge(上接第66页)
TheAlgorithmofWeightFactorofThree
TimesRationalB6zierCurVeThrough
AnyTwoPointsofControlPolygon
YANGCun—dianlYANGWen—qi2
(1.MathsDept.ofShall酉uoTeacherSConegeShangzhou,shaan妇,726000;
2.Maths.Dept.BaojiArBandSci.,BaojiShaanxi721007)
Abstract:If缸lytwopo迦tsofcon娃olpolygonare百Ven'basedonthede缸itionofvectorandcrossproduct,、访tht11euseof廿ian直earea,tlleweightQctorofthreetimesra七ionalB∈ziercurveiscoIlsructedaIldconsequentlythe出reedmesradonalB6ziercurvethrou曲anycwopointsofcan汀01p01ygon.
KeyWord:rationalcuⅣe;conrt01p01ygon;weight6ctor
(上接第70页)
rI’heD蜮印0fP0werF曲拍叫TeadliIlgP似七ss
PANGHorg—tao
(ShangzhouNo珊alSchool,Shangzhou,Shaanxi,726000)
Abstract:Beginningwiththedif.ferentcodomainoftheexponent凡=罢一ofthepowerfhnctiony=x4,the
p
authordiscussespowerfhnction,sdomainbfde6nition,codomain,picture,propertiesandtheirintemalI.elationssothatthestudentscanmasterthepropertiesofpowerf-unction.
KeyWordb:powerfunction;powerfunctionpicture;properties;teachingpmcessdesign
幂函数的教学过程设计作者:
作者单位:
刊名:
英文刊名:
年,卷(期):庞洪涛, PANG Horg-tao商州师范学校,陕西,商州,726000商洛师范专科学校学报JOURNAL OF SHANGLUO TEACHERS COLLEGE2002,16(1)
参考文献(1条)
1. 杜有长 幂函数特点及内在联系 1988(06)
本文链接:http://d.g.wanfangdata.com.cn/Periodical_slsfzkxxxb200201025.aspx



 用户67863212
用户67863212

