2221.,(,)已知圆的方程求经过圆上一点的切线方程。xyrMxy,, 00
2222【结论1】过圆上一点的切线方程xyrMxyxxyyr,,,,(,):。 0000
【】1.设出直线,再求解;
2.利用轨迹思想,用向量或平面几何知识求解。
2222【】对于坐标平面内任一点xx,yy,rM(x,y)x,y,r,直线L:与圆O:0000究竟是什么关系呢?下面我们进行探究: 一、当点M在圆O上时,直线L是圆的切线。 二、当点M在圆O外时,
1.直线L不是圆O的切线,下面证明之:
2r22?圆心O到L的距离为M(x,y)x,y,rd,,由在圆O外,得 000022x,y
?,故直线L与圆O相交. d,r
2.此时直线L与过点M的圆的切线又是什么关系呢? y首先研究L的特征: ,y)M(xL00易知:OML。 ,A
2r222rxy,,,, 00ox22xy,B00
2图1?,,OAONOM,(N为L与OM的交点) 从而OAMA,MA为圆的一条切线, ,
故直线L为过点M的圆的两条切线的两个切点所在的直线。 事实上(另证),
如图1,设过点M的圆O的两条切线为L,L,切点分别为A、B, 12
22则直线MA:xx,yy,rxx,yy,r,直线MB:. 1122?点M的坐标(x,y)满足直线MA与MB的方程, 00
2,xx,yy,r,1010?, ,2,xx,yy,r2010,
2由此可见A、B的坐标均满足方程xx,yy,r, 00由于两点确定一条直线
2?直线AB的方程为xx,yy,r。 00
所以此时的直线L是经过点P的切点弦AB所在直线的方程,而不是圆O的切线。
【】上述点M、直线L实质上是射影几何中的极点和极线。
特别的,当M在圆上时,极线即为切线。
三、当点M在圆O内时,
1.直线L也不是圆O的切线。下面给出证明:
2r22?圆心O到L的距离为M(x,y)x,y,r,由在圆O内,得 d,000022x,y
? 故直线L与圆O相离. d,r
y2.此时直线L与圆的切线的关系又如何呢? LLP0首先研究L的特征: A由上述探讨过程易知, Mo直线LxOM, ,B
此外,L一定过点P(P为两切线的交点,ABOM), ,图2从而L就在图2中过点P且与AB平行的位置处。 事实上(另证),
xy?直线L的斜率00,,,,而直线OM的斜率, kklomyx00? L,OM
一方面,过点M与OM垂直的直线(x,x)x,(y,y)y,0,L方程为 00000
22即 xx,yy,x,y0000
2,xx,yy,r00,另一方面,将直线OM与L的方程联立, y,0y,x,x0,
22xryr00得到它们的交点P的坐标为, (,)2222x,yx,y0000
22xryr200由(二)可知过点P的圆的切点弦所在直线的方程为, ,x,,y,r2222x,yx,y0000
22即L,即为直线的方程。 xx,yy,x,y00000
由此我们看到L?,直线L是由点M确定的。 L0
另外,直线L是过点M的弦(除O,M的弦)的两个端点的圆的两条切线的交点轨迹,
证明如下:
2设,,,,xxyyr,,Pxy(,),由(二)可知动弦AB的方程为,
22又因为点M在AB上,则,,,,xxyyr,,xx,yy,rxy,,以x,y分别代,则。 豆0000
丁致力于构建全球领先的文档发布与销售平台,面向世界范围提供便捷、安全、专业、有效的文
档营销服务。包括中国、日本、韩国、北美、欧洲等在内的豆丁全球分站,将面向全球各地的文
档拥有者和代理商提供服务,帮助他们把文档发行到世界的每一个角落。豆丁正在全球各地建立
便捷、安全、高效的支付与兑换渠道,为每一位用户提供优质的文档交易和账务服务。
圆的切点弦方程
圆的切点弦方程
1. 已知圆的方程x +y =r , 求经过圆上一点M (x 0, y 0) 的切线方程。 【结论1】过圆x +y =r 上一点M (x 0, y 0) 的切线方程:xx 0+yy 0=r 。【方法】1. 设出直线,再求解;
2. 利用轨迹思想,用向量或平面几何知识求解。
【问题】对于坐标平面内任一点M (x 0, y 0) ,直线L :x 0x +y 0y =r 2与圆O :x 2+y 2=r 2究竟是什么关系呢?下面我们进行探究: 一、当点M 在圆O 上时,直线L 是圆的切线。 二、当点M 在圆O 外时,
1. 直线L 不是圆O 的切线,下面证明之: ∵圆心O 到L 的距离为d =
r
22
2
2
2
2
2
2
2
2
x +y
, 由M (x 0, y 0) 在圆O 外, 得x 0+y 0
22
>r
∴d <,故直线l 与圆o="">
2. 此时直线L 与过点M 的圆的切线又是什么关系呢? 首先研究L 的特征: 易知:OM ⊥L 。
r =
2
2
2
∴O A =O N ?O M , (N为L 与OM 的交点)
从而OA ⊥MA ,MA 为圆的一条切线,
故直线L 为过点M 的圆的两条切线的两个切点所在的直线。 事实上(另证),
如图1,设过点M 的圆O 的两条切线为L 1,L 2, 切点分别为A 、B, 则直线MA:x 1x +y 1y =r ,直线MB:x 2x +y 2y =r . ∵点M 的坐标(x 0, y 0) 满足直线MA 与MB 的方程, ∴
2
??x 1x 0+y 1y 0=r
, ?2
?x 2x 0+y 1y 0=r
22
2
由此可见A 、B 的坐标均满足方程x 0x +y 0y =r ,
由于两点确定一条直线
2
∴直线AB 的方程为x 0x +y 0y =r 。
所以此时的直线L 是经过点P 的切点弦AB 所在直线的方程,而不是圆O 的切线。 【注】上述点M 、直线L 实质上是射影几何中的极点和极线。
特别的,当M 在圆上时,极线即为切线。 三、当点M 在圆O 内时,
1. 直线L 也不是圆O 的切线。下面给出证明: ∵圆心O 到L 的距离为d =
r
22
2
x +y
,由M (x 0, y 0) 在圆O 内, 得x 0+y 0
22
<>
∴d > 故直线L 与圆O 相离.
2. 此时直线L 与圆的切线的关系又如何呢? 首先研究L 的特征: 由上述探讨过程易知, 直线L ⊥OM ,
此外,L 一定过点P (P 为两切线的交点,AB ⊥OM ), 从而L 就在图2中过点P 且与AB 平行的位置处。 事实上(另证), ∵直线L 的斜率k l =-∴L ⊥OM
x 0y 0
,而直线OM 的斜率k om =
y 0x 0
,
一方面,过点M 与OM 垂直的直线L 0方程为(x -x 0) x 0+(y -y 0) y 0=0, 即x 0x +y 0y =x 0+y 0
?x 0x +y 0y =r 2
?
另一方面,将直线OM 与L 的方程联立?, y 0
y =x ?
x 0
?
2
2
得到它们的交点P 的坐标为(
x 0r
2
2
2
,
y 0r
2
2
2
) ,
x 0+y 0x 0+y 0
由(二)可知过点P 的圆的切点弦所在直线的方程为
x 0r
2
2
2
x 0+y 0
?x +
y 0r
2
2
2
x 0+y 0
?y =r ,
2
即x 0x +y 0y =x 0+y 0,即为直线L 0的方程。 由此我们看到L ∥L 0,直线L 是由点M 确定的。
另外,直线L 是过点M 的弦(除O ,M 的弦)的两个端点的圆的两条切线的交点轨迹, 证明如下:
设P (x ', y '), 由(二)可知动弦AB 的方程为x 'x +y 'y =r ,
22
又因为点M 在AB 上,则x 'x 0+y 'y 0=r ,以x ,y 分别代x ', y ',则x 0x +y 0y =r 。
22
2
圆的切线和切点弦方程
圆的切线和切点弦方程?
???黄继红???
????
数学是关于现实世界的空间形式和数量关系的科学,其研究的对象是数与形。通常数中隐含着形的关系,形中又展示着数的信息。引导学生多方位地观察问题,通过联想促成数与形的相互转化,揭示出被掩盖着的数形关系,可以帮助学生理解问题的本质,达到培养学生思维灵活性的目的。关于“圆的切线和切点弦方程”的教学,我已经尝试过很多次,但是每次教学后总感觉不过瘾。最近,我通过?“向量的数量积”解决“圆的切线和切点弦方程”?进行了一次教学探究,从数形关系的本质入手,终于感觉“爽”了一把。下面是这节课设计的一组问题链。?
问题1(上海教育出版社高级中学课本高中二年级第二学期(试用本)P38例3)??已知M (x 0, y 0) 为圆C :x 2+y 2=r 2上一点,求过点M 的圆C 的切线l 的方程。?
学生的解答大约也就两种:?
解法(1)当切线l 的斜率存在即y 0≠0时,切线l 的方程为
y -y 0=-
x 0
(x -x 0) ,即x 0x +y 0y =x 02+y 02,因为M (x 0, y 0) 为圆C :x 2+y 2=r 2y 0
上一点,所以x 02+y 02=r 2,?
则切线l 的方程为x 0x +y 0y =r 2;当切线l 的斜率不存在即y 0=0时,切线l 的方程为x =x 0,因为x 02=r 2,所以切线l 方程也可改写为x 0x +y 0y =r 2。?综上,过点M 的圆C 的切线l 的方程为x 0x +y 0y =r 2。?
解法(2)由题意得,CM =(x 0, y 0) 是直线l 的一个法向量,于是可得切
线l 的点法向式方程为x 0(x -x 0) +y 0(y -y 0) =0,即x 0x +y 0y =x 02+y 02,因为
M (x 0, y 0) 为圆C :x 2+y 2=r 2上一点,所以x 02+y 02=r 2,则切线l 的方程为x 0x +y 0y =r 2。?
通过讨论,学生都认为解法(2)优越于解法(1)。解法(2)的本质是利
用直线l 上的任意一点P (x , y ) 满足CM ?MP =0的关系而得,为此请同学们再思
考一下CM 与CP 有何关系?不一会儿,有的说CP 在CM 方向上的投影是r ;还
有的说CM ?CP =r 2等。?
那么,你们是否还有解决问题1的方法??
解法(3)任取直线l 上的点P (x , y ) ,由题意得CM ?CP =r 2,则过点M 的圆C 的切线l 的方程为x 0x +y 0y =r 2。?
问题2你能以问题1为出发点,通过变换条件或结论,提出一些新的探索性的问题吗??
学生思考、讨论后的回答:?
(1)(将圆方程一般化)把题设中的圆C :x 2+y 2=r 2改为圆
C :(x -a ) 2+(y -b ) 2=r 2,求过点M 的圆C 的切线l 的方程。?
探究:同学们通过讨论,一致选用解决问题1的方法(3)处理本问题,
即:任取直线l 上的点P (x , y ) ,由题意得CM ?CP =r 2,则过点M 的圆C 的
切线l 的方程为(x 0-a ) (x -a ) +(y 0-b )(y -b ) =r 2。?
此时,老师可以指出:因为条件一般化了,所以结论自然也一般化了(当
a =b =0时即为问题1的结论)。?
(2)(将条件与结论互换)已知M (x 0, y 0) 为圆C :x 2+y 2=r 2上一点,直线l :
x 0x +y 0y =r 2,请问直线l 与圆C 是否相切???。?(结论成立,因为圆心C 到直线l 的距离为r )
(3)(改变点M 与圆的关系)已知M (x 0, y 0) 为圆C :x 2+y 2=r 2外一点,求过点M 的圆C 的切线l 的方程。?
探究:过圆外一点M (x 0, y 0) 的切线方程可设为y -y 0=k (x -x 0) ,再利用相切条件求k ,这时必有两条切线,注意不要漏掉平行于y 轴的切线。?(4)(引申)已知M (x 0, y 0) 为圆C :x 2+y 2=r 2外一点,设过点M 的圆C 的两条切线MA 、MB ,其中A 、B 为切点,求直线AB 的方程(亦称切点弦所在的直线方程)。?
探究:?
方法1设A (x 1, y 1) 、B (x 2, y 2) ,则切线MA 方程为x 1x +y 1y =r 2,因为
M (x 0, y 0) 在直线MA 上,所以x 0x 1+y 0y 1=r 2,同理可得x 0x 2+y 0y 2=r 2,又直线x 0x +y 0y =r 2(x 0、y 0不全为0)过点A (x 1, y 1) 、B (x 2, y 2) ,因此直线AB 的方程为x 0x +y 0y =r 2。?
显然,求切点弦所在的直线AB 方程这种设而不求的方法实在是难以想到,其结果更是让人觉得意外,怎么与问题1的结论雷同?既然如此,同学们能否另辟蹊径求切点弦所在的直线AB 方程??
方法2因为x 0x +y 0y =r 等价于CM ?CP =r 2(设直线AB 上的任一点
2
P (x , y ) ),所以下面只需证明CM ?CP =r 2即可。?
CB 和CM ,连结CA 、设CM 和AB 交于T ,得CA ⊥MA , CB ⊥MB ,且CM
垂直且平分线段AB ,任取直线AB 上的点P (x , y ) ,则CP 在CM 方向上的投
影是CT ,又CT ?CM =CA =r ,所以CM ?CP =r 2,于是直线AB 的方程
2
2
为x 0x +y 0y =r 2。?
问题3由上述问题的讨论,关于圆的切线和切点弦方程的问题,你能得到怎样的一般结论??
一般地,已知M (x 0, y 0) 为圆C :(x -a ) 2+(y -b ) 2=r 2上一点,则过点M 的圆C 的切线l 的方程为(x 0-a ) (x -a ) +(y 0-b )(y -b ) =r 2;?
已知M (x 0, y 0) 为圆C :(x -a ) 2+(y -b ) 2=r 2外一点,由点M (x 0, y 0) 引圆C 的两条切线MA 、MB ,其中A 、B 为切点,则直线AB 的方程为
(x 0-a )(x -a ) +(y 0-b )(y -b ) =r 2。?
问题4若M (x 0, y 0) 为圆C :x 2+y 2=r 2内的点,直线l :x 0x +y 0y =r 2,请问l 与圆C 的位置关系如何??
探究:首先由圆心C 到直线l 的距离大于r ,所以直线l 与圆C 相离,其
次因为直线l 上的任意一点P (x , y ) 仍然满足CM ?CP =r 2,那么可以证明:连
接CM ,过M 作CM 的垂线交圆C :x 2+y 2=r 2于A、B两点,过A 作圆
C :x 2+y 2=r 2的切线交CM 的延长线于Q,过Q 且与直线CM 垂直的直线即为直线l。?
问题5(作为课后作业)设圆C :(x -a ) 2+(y -b ) 2=r 2,点M (x 0, y 0) ,?直线l :
(x 0-a )(x -a ) +(y 0-b )(y -b ) =r 2?
?(1)若M 在圆C 上,判断l 与圆C 的位置关系并作图表示;??(2)若M 在圆C 内,判断l 与圆C 的位置关系并作图表示;??(3)若M 在圆C 外,判断l 与圆C 的位置关系并作图表示。?
向量的数量积的定义a ?b =a ?b cos θ=x 1x 2+y 1y 2(这里θ为a =(x 1, y 1)与
b =(x 2, y 2)的夹角)应能得到广泛应用,值得品味。加强几何直观,重视图形
在数学学习中的作用,揭示研究对象的性质和关系,这是提高学生数学思维能力的重要途径之一,我们将不断为之努力。?
圆的切线和切点弦方程
圆的切线和切点弦方程
8—3五数学教学2009年第8期
圆的切线和切点弦方程
201600上海市松江二中黄继红
数学是关于现实世界的空间形式和数量关 系的科学,其研究的对象是数与形.通常数中隐 含着形的关系,形中又展示着数的信息.引导学 生多方位地观察问题,通过联想促成数与形的相 互转化,揭示出被掩盖着的数形关系,可以帮助 学生理解问题的本质,达到培养学生思维灵活性 的目的.关于"圆的切线和切点弦方程"的教学, 我已经尝试过多次,但是每次教学后自己总感觉 不够满意.最近,我通过"向量的数量'解决这 个问题,进行了一次教学探究,从数形关系的本 质入手,终于感觉"爽"了一把.下面是这节课设 计的一组问题链.
问题1(上海教育出版社高级中学课本 高中二年级第二学期(试用本)P.38例3)已知 M(xo,Yo)为圆C:X2+Y2=r上一点,求
过点M的圆的切线2的方程.
学生的解答大约有两种:
解法l:当切线f的斜率存在即?0时,切 线2的方程为Y-Yo=一(—z0),即Xox+yoy =02
1_0
2
,因为M(xo,yo)为圆C:X2+.=7'2
上一点,所以a+3=r,则切线f的方程为 XOX+YoY=r2;当切线2的斜率不存在即Yo= 0时,切线f的方程为X=0,因为a=r2-所以 切线2方程也可改写为XoX+YoY=r2.综上,过 点M的圆的切线!的方程为XoX+YoY=7'. 解法2:由题意得,C=(XO,Yo)是直线l的 一
个法向量,于是可得切线2的点法向式方程为 Xo(X—XO)+Yo(Y—Yo)=0,即XoX+YoY= X3+,因为M(0,Yo)为圆C:2+Y=7'2 上一点,所以3+a=?',则切线f的方程为 0+YoY=r2.
通过讨论,学生都认为解法2优越于解法1. 解法2的本质是利用直线f上的任意一点尸(,Y) 满足商.:0的关系而得,为此请同学
们再思考一下商与有何关系?不一会儿, 有的说尸在M方向上的投影是r;还有的说 M?P=r2等.那么,你们是否还有解决问 题1的方法?
解法3:任取直线c上的点P(x,),由题意得 M?P=r2,则过点M的圆的切线l的方
程为XoX+YoY=7'2.
问题2你能以问题1为出发点,通过变换 条件或结论,提出一些新的探索性的问题吗? 学生思考,讨论后的回答:
(1)(将圆方程一般化)把题设中的圆C:0 +.=r2改为圆C:(一0)2十(Y一6)=7'., 求过点M的圆的切线f的方程.
探究:同学们通过讨论,一致选用解决问题1
的解法3处理本问题,即:任取直线f上的点 P(,),由题意得c?p=7.2,则过点
的圆c的切线f的方程为(TO一口)(—a)+(Yo一 6)(一b)=7'
此时,老师可以指出:因为条件一般化了,所 以结论自然也一般化了(当a=b=0时即为问 题1的结论).
(2)(将条件与结论互换)已知M(xo,Yo)为 圆C:+Y2=7'2上一点,直线l:XOX+ YoY=r2
,请问直线2与圆是否相切?
(结论成立,因为圆心C到直线f的距离为r). (3)(改变点M与圆的关系)已知M(xo,Yo) 为圆C:z+Y=r2外一点,求过点M的圆 的切线2的方程.
探究:过圆外一点M(xo,Yo)的切线方程可 设为Y—Yo=(—o),再利用相切条件求k, 这时必有两条切线,注意不要漏掉平行于轴的 切线.
(4)(引申)已知M(xo,Yo)为圆C:X2+0= r外一点,设过点的圆C的两条切线, MB,其中A,B为切点,求直线AB的方程(亦 称切点弦所在的直线方程).
2009年第8期数学教学8-35
探究:
方法1:A(xl,u1),B(x2,y2),则切线MA 方程为1X+YlY=7'2,因为M(xo,Yo)在直线 M上,所以XoXl+蜘l=r2,同理可得XoX2+ YoY2=r.由直线XOX+YoY=7'2(zo,珈不
全为0)过点A(xl,1),B(x2,2),因此直线AB 的方程为XoX+YoY=r.
显然,求切点弦所在的直线AB方程这种设 而不求的方法实在是难以想到,其结果更是让人 觉得意外,怎么与问题1的结论雷同?既然如此, 同学们能否另辟蹊径求切点弦所在的直线AB方 程?
方法2:因为XoX+YoY=?'2等价于M?
任一点P,)),所以 CP:r2(设直线AB上的
下面只需证明?P=7.2即可.
连结,B和M,设M和B交于
,得上,上MB,且M垂直且平
分线段AB,任取直线AB上的点P(,),则P 在CM方向上的投影是lCTI.又lCTI.1CMl= ICAI=r,所以CM-=r2,于是直线AB
的方程为XOX+YoY=r2.
问题3由上述问题的讨论,关于圆的切线 和切点弦方程的问题,你能得到怎样的一般结 论?
一
般地,已知M(xo,Yo)为圆C:(X—n)2+ (一6)=r2上一点,则过点M的圆的切线f 的方程为(XO一0)(—a)+(Yo一6)(一b)=r2; 已知M(xo,Yo)为圆C:(一0)2+(Y一
(上接第8-33页)
分析:把与6l,62,63相连的树权的个数变 为6,相应的与6l相连的有食物的树杈的个数变 为2,与62相连的有食物的树权的个数变为3,问 题等价转化为古典概型问题了.画树形图(图略)
可得,蚂蚁共有18种不同的走法,其中5种走法 获得食物,获得食物的概率为羔.
变式题二:在原题背景下,把与6l相连的树 权个数改为4个,其中2个树权上有食物;与62相 连的树权的个数改为6个,其中4个树权上有食 物;与63相连的树权共有7个,没有树权上有食 物,求蚂蚁获得食物的概率.
分析:第二层树杈上有食物的第一层树权是
,由点M(xo,Yo)引圆的两条 6)=r外一点
切线M,MB,其中,B为切点,则直线AB 的方程为(XO一0)(—a)+(Yo一6)(一b)=r2. 问题4若M(xo,yo)为圆C:+Y2=r2 内的点,直线Z:XOX+YoY=?'2,请问Z与圆C 的位置关系如何?
探究:首先由圆心到直线f的距离大于r, 所以直线f与圆相离.其次因为直线f上的任 意一点P(x,Y)仍然满足C?Cp=r2,因此可 以证明:连结M,过作的垂线交圆C: 2+Y0=r2于A,B两点,过A作圆C:2+ Y2=r2的切线交CM的延长线于Q,过Q且与 直线M垂直的直线即为直线f.
问题5(作为课后作业)设圆C:(x-a)+ (y-b)2=r,点M(xo,uo),直线f:(XO-a)(x- a)+(Yo一6)(—b)=r2.
(1)若M在圆上,判断f与圆的位置关
系并作图表示;
(2)若M在圆C内,判断f与圆的位置关 系并作图表示;
(3)若M在圆C外,判断f与圆的位置关
系并作图表示.
向量的数量积的定义.6.=l1.IblCOS :XlX2+YlY2(这里为=(z1,Yx)与b=
(2,)的夹角)应能得到广泛应用,值得品味. 加强几何直观,重视图形在数学学习中的作用, 揭示研究对象的性质和关系,这是提高学生数学 思维能力的重要途径之一,我们将不断为之努力. 61,62,与它们相连的小树权的个数分别是4和 6,它们的最小公倍数是12,因此,将第二层树权 的个数变为12,同时与61相连的有食物树权个 数变为6,与62相连的有食物树权个数变为8;与 63相连的小树权上没有食物,与之相连的树权的 个数直接变为12.问题变为古典概型问题,画树 形图(图略)容易求出蚂蚁获得食物的概率为. 参考文献
【1】田载今.概率树【J】_中学数学教学参考, 2008,8(下半月?初中):34—35.
【2】盖仕广.利用转化思想巧解一道课本习题 一
兼与胡其忠老师商榷[J】.中学数学杂志,2008 (6):59—60.
圆锥曲线的切点弦方程
2011年江西高考一道试题解法的推广──圆锥曲线的切点弦方程
圆锥曲线问题是高考的重点,曲线的切线又是近几年的热点,这类题对学生的要求比较高,充分考查学生的逻辑思维能力,本文在对江西高考试题分析的基础上归纳总结出圆、椭圆、抛物线、双曲线的切点弦方程的求法。
背景知识
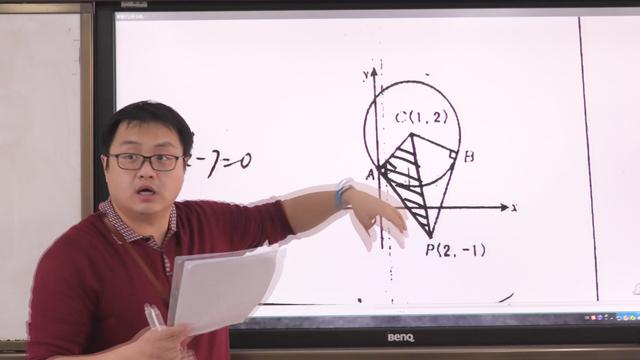
已知圆C:x?y?r
程.
分析:易知以A?x0,y0?为切点的直线方程为:xx0?yy0?r
(2011年江西高考理科第14题) 2222求以点A为切点的切线方?r?0?,点A?x0,y0?是圆C上一点,?r?0?
x2y2?1?22问题1:若椭圆2?2?1的焦点在x轴上,过点?1,?作圆x?y?1的切线,切ab?2?
点分别为A、B,直线AB恰好经过椭圆的右焦点和上顶点,则椭圆方程是__________. 解:设A?x1,y1?,B?x2,y2?
∵点A、B在圆x2?y2?1上,则
过点A?x1,y1?的切线方程为L1:x1x?y1y?1.
过点B?x2,y2?的切线方程为L2:x2x?y2y?1.
由于L1,L2经过点?1,?则x1??1?
?2?11y1?1,x2?y2?1. 22
1y?1的解。 2
1∴经过A、B两点的直线方程AB:x?y?1. 2故?x1,y1?,?x2,y2?均为方程x?
x2y2
设椭圆2?2?1的右焦点为?c,0?,上顶点为?0,b?. ab
由于直线AB经过椭圆右焦点和上顶点。
?c?1,b?1即b?2 2
?a2?b2?c2?5 x2y2
??1. 故椭圆方程为54
由此题的解题方法,可得到如下推广:
结论一:(圆的切点弦方程)
过圆x?y?r222?r?0?,外一点P?a,b?作圆的两切线,切点为M、N,则直线MN的方程为:ax?by?r2.
x2y2
??1外一点P?1,2?作椭圆的两切线,问题2:过椭圆切点为M、N求直线MN43
的方程.
解:设M?x1,y1?,N?x2,y2?则过M、N的切线方程分别为;
x1xy1yxxyy??1,2?2?1 4343
xxyyxxyy由于两切线都过P?1,2?,则1?1?1① 2?2?1② 4343
x2yx2y?1经过M、N,所以直线MN的方程为:??1。 这两式表示直线?4343
结论二:(椭圆的切点弦方程) x2y2
过椭圆2?2?1?a?b?0?外一点P?x0,y0?作椭圆的两切线,切点为ab
M、N则直线MN的方程为:
2x0xy0y?2?1 a2b问题3:过抛物线y?4x外一点P??1,?2?作抛物线两切线,切点分别为M、N,
求直线MN的方程。
解:设M?1,x?1y,?N?x2过yM、N2,则的切线方程为y1y?2?x?x1?,y2y?2?x?x2?
由于过M、N的切线都经过P??1,?2?则?2y1?2?x1?1?,?2y2?2?x2?1? ∴直线MN的方程为?2y?2?x?1?即x?y?1?0
结论三:(抛物线的切点弦方程)
过抛物线y?2px?p?0?外一点P?x0,y0?作两切线,切点为M、N,则直2
线MN的方程为yy0?p?x?x0?.
x2y2
??1外一点P?3,3?作双曲线两切线,切点分别为M、N,问题4:过双曲线54
求直线MN的方程。
解:设两切点的坐标为M?x1,y1?,N?x2,y2?则两切线方程为
x1xy1yxxyy??1,2?2?1, 5454
3x3y3x3y由于两切线均过P?3,3?则1?1?1,2?2?1 5454
3x3y??1的解, 故?x1,y1?,?x2,y2?均为方程54
3x3y??1 则过M、N的直线方程为:54
结论四:(双曲线的切点弦方程) x2y2
过双曲线2?2?1外一点P?x0,y0?作双曲线两切线,切点分别为M、N则直线ab
MN的方程为:
x0xy0y?2?1. a2b



 爱冰冰
爱冰冰

