1、(2007四资阳)如图8-1,
对角线AC上一点(不与A、C重合),PE?BC于点E,PF
?CD于点F.
(1) 求证:BP=DP;
(2) 如图8-2,
旋转,在旋转过程中
明;若不是,请用反例加以说; 图8-1 8-2 (3) 试选正方形ABCD的两个顶点,
PECF的两个顶点连结,使得到的
长度始终相等,并证明
2、(2007甘肃陇南)四
(2)观察图形,猜
并证明你的猜想(
AEF3、(2007江苏扬州)如图,正方绕逆时针旋转后得到正方,边nABCDAEFG与交
(1)以图中已标有字母的点为端点连两线段(正方形的对线除),要求所连结的两条线段相交且相
432cm(2)若正方形的边长,重叠部分(边
E
B A
A4、(2007浙江台州)把正方形点,按顺时针方向旋
HBH与交于点(如图)(试问线段与
请先观察猜想,然后再证
D C
G
H
F A B
E
(第5题)
5((本题10分)
BDEAFBDF如图1,在正方形中,角线与相交于点,平
1(1)求证:; EFACAB,,2
BBACA(2)点从点发,沿着向点运动(不与点重
BACACA沿着的延长运动,点的动速度相同,当动
BDFEAC,AF,BACFFE之停止
1ABEF请猜想,三者之的数量关系,并证
BDAE,3CE,2(3)在(2)的条件下,当,时,求的长( 1111
A E1A D D A
DAFE E 1F
F 1 CB CB CB图1 C 1
图2
(第27题图)
(5)(13分)如图,正方形ABCD中,过DDE?AC,?ACE =,CE
6、 (2007开封) (本题
内一点,在正方形ABCD外有一点E,
满足?ABE,?CBP,BE,BP, DA(1) 求证:?CPB??AEB;
P(2) 求证:PB?BE;
E
BC 图 7
FAF7.(2007海南),本题满12分,如图11,在正
BDEBCG于点,交的
,ADE,CDE(1)求证:?;
HCCH,CEFGFH,GH(2)过
AD,1,ECG(3),,试问否在的值,使为等腰
的值;若不存在,请
AD
E
F
H
BGC
((2007常)(本小
已知,如图,正方形ABCD的边长为6,形EFGH的三个顶点E、G、H分在正方形 ABCDAB、CD、DA上,AH=2,连结CF( GCD(1)当DG=2时,
(2)设DG=x,用x的代数式
F(3)判断?FCG的面积能否等
H
ABEby
正方形的计算与证明
正方形的计算与证明 ECD一、填空
1、已:如图所示,E为正方形ABCD外一点,AE,AD,?ADE,75?,则?AEB,,,,。 BA2、正方ABCD的对角线AC为一边作菱形AEFC,则?FAB,,,,。 3、正形ABCD中,对角线的是10cm,点P是AB上任意一点,则点P到AC、BD的距离之和
A4、如图所示,在正方形ABCD中,M是BC上一点,连结AM,AM的垂直平D分线GH交AB于G,交CD于H,若AM,10cm,则GH,,,。 H5、正方形ABCD和正方形OEFG的边长均为4,O是正形ABCD的
G心,则图中阴影部分的
二、精心选一选~ BCM1、四边形ABCD,O是对角线的交点,下条件能判定这个四边形是正方
A、AC,BD,AB?CD,AB,CD B、AD?BC,?A,?C C、AO,BO,CO,DO,AC?BD D、AC,CO,BO,DO,AB,BC
2、正方形具有而菱形
A、对角线互相平分 B、每条对角平一组对角 C、角线等 D、对边相等 3、以线段AB两个端点A、B为顶点作位置不同的
BA、1个 B、2个 C、3个 D、4个
A4、在正方形ABCD所在平面内找一P,P点与A、B、C、D中点都连在一个等边角形,那么这样的P
5、如图所示,以正方形ABCD中AD为一边向外作等
6、下说法错误的是,, DCA、四个角相等的四边是矩形 B、四条边相等的四形是正方 C、对角线相等的菱形是正方形 D、对角互相垂的形是正方形 DC7、如图所示,在平行四形ABCD中,AD,2DC,M、N分在AB两边的延长线上,且有MA,AB,BN,MC与DN的关系是,,。 GHA、相等 B、
三、说理与简答
1、如图所示,正方形ABCD中,P对线AC上一点,PE?AB于NABME,PF?BC于F。想EF与PD的数量关系、位置关系,
PF
CBE
2、已知:如图所示,在正方形ABCD和方形AEFG有一公顶点A,把正方形AEFG绕A点旋如图所示位置,连结DG、BE。试说
DC
G
F
AB
第 1 页 共 4 页 E
3、已知:如图所示,在正方形ABCD,E、F分别是AD、DC的交点,AF、BE交于点G,结CG,试说明:ΔCGB是等腰三
G F
C B
4、如图所示,在RtΔABC中,?C,90?,?A、?B的分线交于点D,DE?BC于E,DF?AC于F,试说明四边形CEDF
DF
CEB5、如图所示,在正方
DC
N
AMBE
6、已知:如图所示,ABCD是方形,过B作BF?AC,E是BF上一点,四边
F
CD
E BA
7、如图所示,ABCD是正形,AE?DB,BE,BD,BE交AD于F,试说明:ΔDEF是
AD
O
E FG BC
?
8、如图?所示,已知正方形ABCD对线AC、BD相
F E
第 2 页 共 4 页 CD
9、如图所示,点M是矩形ABCD的边AD的中点,点PBC边上一动AMD点,PE?MC,PF?BM,垂足分别E、F。 E?当矩形ABCD的长与宽满足什么条件时,四边形PEMF为矩形,
?在?中,当点P运到什么位时,矩形PEMF
10、如图所示,正方形ABCD中,E、F分别是BC、CD上点,AE、ADDE、BF、AF把形分成8个小块,每个小块的面积分别
S8。?试比较S3与S2,S7,S8的小,并说明理由;?前述问题条5S8S件中的正方形ABCD变为ABCD,其余条件不变,上述
3 S6FS 1S
7S 4S2S CBE
11、如图所示,在矩形ABCD中,AB,24cm,BC,12cm,点P沿AB边从点A开始点B以2cm/s的速度移动,点Q沿DA边
?当t为何值时,ΔQAP为
?求出此时四边形QAPC面积,并提出一
DC
Q
ABP
12、作:将一把三角尺放中正方形ABCD中,并它的直角顶点F在对角线AC上滑动,直角一边始终经过点B,另一边与射线DC相交点Q,探究:?当点Q在DC上时,线段PQ线段PB之间有怎样的大小关系,试说你观到的结论;?当点Q在DC的长线上,?中你观察到的结论还成立吗,说明理由。,
AAADDD
P
PQ
CBBBCC ???Q
13、已知:如图所示,在正形ABCD中,?EAD,?EDA,15?,试说AD明:ΔBEC是
E
CB第 3 页 共 4 页
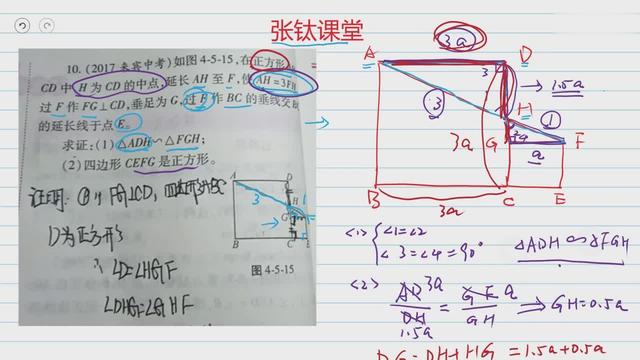
14、如图所示,在正方ABCD
CD于H,G为FH中点,求
D A
E
H G
B CF
第 4 页
将大正方形分割成若干小正方形的一种简捷方法
中学数
2 0 0
9将
大 正方 形 分成割 若 干 正小 方 形的一
广大州 附学 中属学 ( 5 10 0 5 0) 昌颜明 湖
省双南县第三小牌学 (4 252 0 0) 蒋玲玲
一 个将的正 方形 成割若 干 个 小的正 方形 问 在小 学数题 学题特 是小别 数 学竞学赛 题经中 出常 .现 下如 就面 是道两 见常的 数竞学 题 : 赛1 . 将 一 个方
能取(
A. 4 . 5B
)
. 8 C . 9D
(
第六十 江苏届 初
2 试.设 计一 方种法 , 一个把正 方
图
.4
5
图6
图
那么 k× 的分阶 割擦 去 格线 将,一 个 ( 一 1)X ( 1 ) 一阶正 方合形 成一个 大正方 形 这,时 剩 余 的 就 有 还× k 一 (1k )X ( 一1 )1+=2k , 显
k足≥,2 从而我们 得 到 了将
漏 分地成 割个8正方 形 (分得 的正 方形 大小 可 以 同相 ; 又) 如何 正 方 形
方. 形 ( 1 99 7 安年 省徽 中初数 学竞赛 题) 很 多 究的 割 方
形
分 割成 于 2偶 的 数个 正方 所有 分 法. 我们 这 将种 分割 为称数偶分 割. 还 我可 在以上 面 的偶 数 割 分, 将 其某中 个 方 形进 行 正2 2× 分割, 此 时 多 会3个 方, 故上面 的所有偶 数 分 中割就得会到
并
取得了好较的 成 果¨ . 他们得到
任 意一正个方 都 可形 被以割分成 ( 为 除n 2 、3 、 5外 的正 整 数) 正 形方 . 他 们对 结 果证的明
较对繁 ,人 他们研 究在的基 上 础给 出一 相种对 较 单 简的证明 .面 是 人本 在 种一相 对简 的捷 分割 方 基上础 对个这 论结给
2 I j +} 3 (其中 k≥ 2 ) . 样就这
奇切数 分割 .
次 依上 通的三 分割 , 就得 我到了结 果: 任 意个 一方 形都正 可以 分割成 n ( n 除为2 、 3 、 5外 的 整 数)个 正方 形 按 .上面 分 的方法 很割容 解易 答本文
我
知道 们 采,均取分 方式的很容
形 别分分 割 成 下列 个 数 的正 方 形 : 2 , 3 , 4 ,…
… ,
这. 种分割 我称 为 _其j } × 阶
是 就当 分 别
道竞赛. 题一 (江省初竞中题 赛) 选 .第 二( 安徽初题中竞赛题) 分得 8 要,种就是 4= , 即 在4× 4阶分割
3到1 , 就是种 =1 4 , 即 在 411×4阶分 割 中 擦去 1 3 1×3 阶分割 的线格, 其中一的 正个形 进
阶2割 分可即.
:24
3
:9
4 1 =
6值
指得 出, 的面上的割分法只是 目前方相较对 简单 一分 法种 已 而 得要同一
法该应不是 唯一 的 请 , 有趣兴 的 者
续探 索.继
参文献考
1 图
图2
图
3
上 面 在 k的×阶分后 割中 , 适当擦地 去线 格将可 干小正方 形并成 大 的
6所
[ 1] 王季. 美方正形 的分 割 [ ] . J学生中理科
[2 张] 斌 如.将何一大个方正形割成分干小正方
学 . 020 7( 5 )
.
将大正方形分割成若干小正方形的一种简捷方法
将大正方形分割成
捷方法 中学数学研
将大正方形分割成若干小正方形的一种简捷法 广州大
湖南省双牌县第三小学(425200)蒋玲玲
将一个大的方形分割成若干小的正方形 问题在小学数学题特别是小学数学竞赛题中经常出 现.如面就是两道常见的数学竞赛: 1.将个正方形分成n(n>1)个小正方形, 则n
A.4B.5C.8D.9
(第十六届江苏省
2.试设计一种方法,把一个正方形不重复不遗 漏地分割成8个正方形(分的正方形大小可以不 相同);又问如何正形按上述要求分成31个
(1997年安徽
很多的究对分割法进行了较深入的探讨 并取得了较好的成果?儿.他们都得到了一个结果: 任意一个正方形都可以被分割成(n为除2,3,5外 的正数)个正方形.但他们结果的证明还相对 繁,本人他们研究基础上给一种对简 的明.下面是本人在一种相对简捷的分割方法 基础上对这
我们知道,采取均分的方式很容易将一个正方 分别分割成列个数的方
.
这种分割我称其为_j}×阶分割.下图(1,3) 就是当分
2:43:94=16
图1图2图3
在上面的k×后阶分割中,适当地擦去格线可将 若干正方形合并大的正形,
图4.图5图6
那么在k×阶的割中擦格线,将一(一 1)X(一1)阶正方形合并成一个大正方形,这时剩 余的就还有k×一(k一1)X(1)+1=2k,显 然这里的满足k?2,从而我们得了将一个方 形割成2的偶数个正方形的所有分法.我们 将这种分
我还可以在上的偶分割中,其中某一个 正方形进行2×2阶分割,此时就会多出3个正方形, 故上面所有偶数分割中就会得到一个的分割数 2Ij}+3(中k?2).这样就得到了大于等于7的一
依次通过上面的三种分割,我就得到了结果:任 意一个正形都可以分割成n(n为
按上面分割方法容易解本文最前面的 道竞赛题.第一题(江苏省初中竞赛题)选.第二 题(安徽初中竞赛题)要分得8种,就是=4,即在 4×4阶分割中擦去3×3阶分割的格线就;而要得 到31,就是=14,14×14阶分割中擦去13 ×13阶分割的格线,再将其中
2阶分割即可.
值得指出的,上面的割方法只是
简单的一种分法而已要得到同一种分割数目,分割 的方应该不是唯一,请兴趣读
参考文献
[1]王美.正方形的分割[J].中学生理科月刊,2004(2). [2]斌.如何将一个大正方分割成若个小正方
正方形证明
正方形证明
已知:正方形EFGH的四个顶点都在正方形ABCD的
证明:作出如图的辅助线,可知,MJKL是一个
d
∴S△EMF=S△FJG=S△GKH=S△HLE,
∴SAEFB+SCDHG=S△EMF+S△AEN+SNBMF+S△GKH+S△
CPG+SPDHK=S△EMF+(d+m)c+(a+b+b-m)d+ S△GKH+(a+c-d+m)a+
1
2121212
(b+c+b-m)(a+c-d) =2 S△EMF+
12
(cd+cm+ad+2bd-dm+a2+ac-ad+am+2ab+2bc-2bd+ac+c2-cd-am-cm+dm) =2 S△EMF+(a2+c2+2ab+2bc+2ac)
SBCGF+SADHE =S△FJG+S△BOF+SOCGJ+S△HLE+S△DQH+SQAEL=S△FJG+(a+m)d+
111
(a+b+c-d+b-m)a+ S△HLE+(a+c-d)(c+m)+(b+d+b-m) c 222
1
=2 S△FJG+(ad+dm+a2+2ab+ac-ad-am+ac+am+c2+cm-cd-dm+2bc+cd-mc)=2
21
S△FJG+(a2+c2+2ab+2bc+2ac)
2
12
12
∴SAEFB+SCDHG=SBCGF+SADHE.
如下图形都有S1+S2=S3+S4这一性质



 哀思沫
哀思沫

