用matlab 拟和模
Matlab 用以建立数学模型是一个很的工具。对型函数的评价,一个很重要方法就是最小二乘(Least squares)由least mean squares这个法得到。假如有点P(X, Y) ,每点 P(i) 由X(i), Y(i) , i = 1 ~ m 组成;
Y_fit(i) ). ) (i = 1 ~ m)。
一个好的模型,least mean squares就小;另一方面,何得模型参数A ,使得least mean squares 有最小
1
是所谓的,
简介:
模型有线性和非线性之。于线性模型,求参数,其实就是求一步矩阵的逆(稍候我们可以到)。而非性模型,往不能一步就得结果,所以就需多步近。就这样,在众多的多步逼近的方法中,快收敛于最
A: n+1 = A: n + (Hessen ( L ))1 * grad(L)
这里Hessen ( L )是被拟合的模型函数的least mean squares方法的Hessen 矩。grad(L)是她的梯度
这个方法包含了一个求hessen 矩逆的运算。其实,这方法难的不是这个逆,而是如何得到Hessen 矩阵和梯度矩阵。梯度矩还好说,就是least mean squares 方法对各个参数介偏导数。Hessen 矩阵包含了一介偏数的组合(主要是相乘),和二介偏导数。当然,许多模型的介偏导数相对于一介偏导数的合是一个较小的量,别是线性模型,就没有二介偏导(所以,线性
2
求出参数)。于是,方法就利用这个特点,将逼近限制在一介偏导构成的伪Hessen 矩阵上。就诞了
法。
Gauss-Newton 直接用Jacobian 行列式代替 Hessen矩阵,用least squares 值代替梯度(注,不是least mean squares ,因为当用Jacobian 行列代替Hessen 矩阵时,中间有一个自由度的差别)这里的拟合
A: n+1 = A: n + (Jacobian ( L ))1 * L (对L 的定义会在下文中给出)
因为越是接近最(或者临界值),Jacobian ( L ) 就是畸形,所以实际计算机运算中,求逆这一步都
( L ) );
( Jacobian ( L ) )1 --- ( ( Trans(J) * J )1) * Trans(J)
这里Trans()是转置运算。
Levenberg-Marquardt 法比Gauss-Newton 好,可以,在很多时,和Newton 法是一样的(当参数相独立时候,而这个条件是好的数学模型基本条件,虽然时候不能100%保证,但是,基本上参数互相之间相关性
3
Newton 法相,Levenberg-Marquardt 法因为没有纯二介偏导算,速有时候还比Newton 法快。且,Levenberg-Marquardt 法引入了一个步长,使得该方法在计算机运算上,更容易
实现:
下面我们
假设 L = sum ((Y - Y_fit ). ) (Y= [Y (1), Y(2)? Y(m)]是测
F( A(1), A(2)?A(n), X(2))?F( A(1), A(2)?A(n), X(m))] ), 是模型值。其中的X(1)~(m)就是对应于Y 的测量值,A(1)~(n)是模型的
使L 最小的参数A 就是我们要的参。L 线性时,L 的小值,就是要求满足L 对于各个参数的偏导数=0的点(相当于解一个多元一方程组)。当L 线性时,上述件依然有效,就是不能。于是就有逼法。考虑非线性模型二介偏导数不全为零,果给定一个接近最佳参数值的估计参数A:current,最参数(使得L 最小的参数)A:min可
Hessen (L)1 * grad(L)。
4
grad(L)是一个一维向量,第j 个向量g(j)是L 对参数A(j)的
假设F( A, X )对A(j)的一介
g(j)= - 2 * sum[(Y - Y_fit)* D_Y_fit(j)]
Hessen (L)是一个二维的矩阵,第i 行第j 列的值 H(i, j)=2*sum[D_Y_fit(i)* D_Y_fit(j)- (Y - Y_fit)* DD_Y_fit(j, i)]
这里DD_Y_fit(j, i)
偏导
在Levenberg-Marquardt 法中,首先虑到(Y - Y_fit)* DD_Y_fit(j, i)这一
其次,假如参数的互相之
DD_Y_fit(j, i)在i, j相等的时候
间相互交)。再次,考虑到2
于是,LM 法用H’(i, j)(
半)来替Hessen 矩
H’(i, j)= sum[D_Y_fit(i)* D_Y_fit(j)] (i不等于j 时)
H’(i, i)= (1 + r) * sum[D_Y_fit(i)* D_Y_fit(i)]
假设D_A = ( A:min - A:current)是最佳参数和当前估计参
数的差,是一个一
维向量。
LM 法就是
5
1) 假设个r 比如可以从1开始,解
细心的同已经发现了,这是一个线方程,意
D_A = H’ \ ((-1/2)grad(L))
没
2) 比
a) L(A:current + D_A ) L(A:current ),就保留A:current + D_A,并减小r (比如r=r/10)
b) 否则就增加 r(比如r=r*10)
3)
这个方法可以有两个结束指a) r 很大时,说明方程到了平坦区。b) 每一次解方程以后,会比较一次L ,如L 还在减,但是减小幅度很小时,可以束。 实应用中,没用r 小来结束,因为L 变化的减小比r 快。当然,r 很小也是一个结条件,只是,r 还没很小时,L 的变化已经很小了。说明拟合已经十分接近
有一点注意,就是接近终点时计
( Levenberg-Marquardt法)的inv 会变得十分不稳定,
6
就算matlab 说用QR decomposition ,也可能出现错误。如果你用r=1e+20计时,基本matlab backslash 是得到什么结果的。建议用函数inv()来计。或者用经“最大绝对值优先”的Gauss-Jordan 法。他们都比
最小二乘的拟差可以用1/2Hessen矩阵来估计,Levenberg-Marquardt 法中可以r=0的时候的H’的inv 来计算。具体
A 的无偏标准(覆盖68%的置信区间)= +/- sqrt( L/(自由度)* diag(H’1)) 这里,L 是用最后得到的拟合参数计算的方差和,自由度的
自由度 = 拟合样本数(x-y 的个
总结:
matlab 计算非线性最小二的方法大致
1) 定拟合函数F( A, X ),出函数对各
D_Y_fit(1~n)(如果手算有困难,可以用Mathematica 之的支持符号运算软件忙,据说也可以用matlab 符号运算工具箱,不过自己没有试过),如果偏导数比
7
还可以再写
2) 用组估计值作为A:current,计
X ) ). ) (least square)
3) 根据1) 得到的函数,用上面的定义,用估计值A:current构建(-1/2)grad(L) 矩阵G 。第j 个元素g’(j)可以由下面的方法得
g’(j)= sum[(Y - Y_fit)* D_Y_fit(j)]
和H’矩阵(Levenberg-Marquardt 法):
H’(i, j)= sum[D_Y_fit(i)* D_Y_fit(j)] (i不等于j 时)
H’(i, i)= (1 + r) * sum[D_Y_fit(i)* D_Y_fit(i)]
或者1/2Hessen矩
H(i, j)= sum[D_Y_fit(i)* D_Y_fit(j)- (Y - Y_fit)*
DD_Y_fit(j, i)] 因为A 有了,X Y 有了,以面的矩阵都是数字矩
4) 解方程
D_A= H’ \ G (LM法) 或者 D_A= H \ G (Newton 法)
用A:next = A:current + D_A 重新计算2)
注意,计算2) 之前,可对A:next作一个范围检查,对于越过边界条件的值可以修正。方法:i ) 保原来的值;ii ) 用边界件;iii) 对第j 个不合条件的值,取一个小的D_A(j)(
8
到满足条件)。
5) 如果是LM 法,根据上文章,改
a) L(A:next) L(A:current ),就保留A:next (A:current =
A:next),并减小r (比如r=r/10)
b) 否则就增加 r(比如r=r*10)放弃A:next
如
a) L(A:next) L(A:current ),就保留A:next (A:current =
A:next), b) 否则,就结束~说
通常,Newton 法结束
6) 在重复3) 之前,可以用章提到的
7) 全结束了可以根据需要,求个误差。不
用matlab 大致是。 其实写这篇文章的时候,自己正好在做关于非线性拟合的模型。发现matlab 的fit 不能给出数的误,就用以的c++的方法改了一下,放在matlab 里。顺便总结了面的文字,当然,只是自己的理解,如果有什么不完整的,还希望大
下我会帖c++的非
9
Levenberg-Marquardt 方法。大家如有比较棘的函
有任问题,也欢迎大家
freecat 2007-6-22 23:16
想问一下
确
如果函数线性而且非常复杂,而且不能用个函数来描,也就是说F 未
[[i] 本帖最后由 freecat 于 2007-6-22 23:42 编辑 [/i]]
recbio 2007-6-23 22:13
这个题非常好。其实自己也不很清楚这
通常的,如果有规律,且非线性。如果是拟合某一个连续的间,多项式合是可以的(类似原函数的勒展开) 。就是参数的意义不十分明确
如果不连续的,那么就只
实在不行,以用” 枚举” ,建立评价函数,利用计机的速度
10
一般来说,不能100%的解决,还是可在一个比较
当然,具体的方案还需视实际情
狐
建立评价函数,用启发式的迭代优化方法求极值,是一个行之有的方法,虽这种法的收敛性质未必一定稳定,但确实可以在一个比较高的概率范围内解题
freecat 2007-6-23 23:58
[quote]原帖由 [i]recbio[/i] 于 2007-6-23 22:13 发表
[url=http://pic.92to.com/cn/201709/15/back.gif[/img][/url]
这个题非常好。其实自己也不很清楚这
通常的,如果有规律,且非线性。如果是拟合某一个连续的间,多项式合是可以的(类似原函数的勒展开) 。就是参数的意义不十分明确
... [/quote]
我自己的论文也在了这里,对于一个所谓评价函数的求解,倒是可以用所启发式迭代求似最解,但是在函数和参数的一一应关系不明确之前,用传统的梯度迭代法却遇到了
11
百度搜“就爱阅读”,专业资
92to.com,您的在线图书馆
12
精华资料matlab处理非线性误差估计
用matlab拟和模
Matlab用以建立数学模型一个好工具。对模型函数的评价,一个很重要的方法就是最小二乘(Least,squares)由least,mean,squares这个方法到。假如点P(X,,Y),每个点,P(i),X(i),,Y(i),,,i,=,1,~,m组成;
中,A=,A(1),A(2),?,A(n)是模型的n个参数。
least,mean,squares,=,(1/m),*,sum,((Y(i),-,Y_fit(i),).^2) , (i,=,1,~,m
)。
一个好的模型,least,mean,squares就;而另一方面,如何得到模参数A,使得least,mean,squares有最小值,就是所谓的,最小二
(least,squares,curve,fitting)了。
简介:
模型有线性和非线性之。线性模型,求参数,其实就是求一步矩阵的逆(稍候我们可以看)。而非线模型,往不能一步就得结果,以就需多步逼。就这样,在众多的多步逼近的方法中,快收敛于最
A:,n+1,=,A:,n,+,(Hessen,(,L,))^-1 * grad(L)
这里Hessen,(,L,)是被拟合的模型函数的least,mean,squares方法的Hessen矩。grad(L)是她的梯度
这个方法包含了一个求hessen矩阵的逆的运算。其实,个方难的不是这个逆,而是如何得Hessen矩阵和度矩阵。梯度矩阵还好说,就是least,mean,squares方法的对各个参一介偏数。而Hessen矩阵包含了一介偏导组合(主要是相乘),和二介偏导。当然,许多模型二偏导数相对于一偏导数的合是个比较小的量,特别是线性模型,没有二介偏导(所以,线性模型可以直接求出参数)。于是,的方法就利用这个特点,将近限制在一介偏导数构成的伪Hessen矩上。这就诞生两个比较著名的
Gauss-Newton,接用Jacobian,行列式代替,Hessen矩阵,用least,squares值代替梯度(注,不是least,mean,squares,因为当用Jacobian,行列代替Hessen矩阵时,中间有一个自由度的差别)这里的拟合
A:,n+1,=,A:,n,+,(Jacobian,(,L,))^-1 * L , , , ,(对L的定义会在下文中给出)
因为越是接近最值(或者临界值),Jacobian,(,L,)就越畸,所以在实际的计算机运
如,J=,Jacobian,(,L,),);
(,Jacobian,(,L,),)^-1 , ---> , (,(,Trans(J),*,J,)^-1),*,Trans(J)
这里Trans()是转置运算。
Levenberg-Marquardt法比Gauss-Newton好,以说,在很多时,和Newton,法是一样的(当参数互相独立的时候,而这个条件是的数学模型基本的条,虽然有时候不100%保证,但是,基本上数互相之间相性大)。与Newton,相比,Levenberg-Marquardt法因为没有纯的二介偏导运,速度有时候还比Newton,法要快。而且,Levenberg-Marquardt法引入了一个步长,使得该方法在计算机运算上,
实现:
下面我们简说一下这个Levenberg-Marquardt法,
假设,L,=,sum,((Y,-,Y_fit,).^2) , (Y=,[Y,(1),,Y(2)?,Y(m)]是测量值, Y_fit,=,F(,A,,X,)=[,F(,A(1),,A(2)?A(n),,X(1)),,F(,A(1),,A(2)?A(n),,
X(2))?F(,A(1),,A(2)?A(n),,X(m))],),,是模值。中的X(1)~(m)就是应于Y的测量值,A(1)~(n)是模型的参
使L最小的参数A就是我们要求的参数。L线时,L的最小值,就是要求足L对于各个数的偏导数=0的点(相当于解一个多元一次方程组)。当L非线性,上述的条件依然有,就是不能解。就有了逼近法。考虑到非性模型的二介数不全为零,如果给定一接近最佳参数值的估计参A:current,最佳参数(使得L最小
grad(L)是一个一维向量,第j个向量g(j)是L参数A(j)的
假设F(,A,,X,)对A(j)的一介
g(j)=,-,2,*,sum[(Y,-,Y_fit)*,D_Y_fit(j)] Hessen,(L)是一个二维的矩阵,第i行第j列的值
H(i,,j)=2*sum[D_Y_fit(i)*,D_Y_fit(j)-,(Y,-,Y_fit)*,DD_Y_fit(j,,i)]
这里DD_Y_fit(j,,i)是模型函数F(,A,,X,)先A(j)参数求一
在Levenberg-Marquardt法,先考虑到(Y,-,Y_fit)*,DD_Y_fit(j,,i)这一项,在接近最佳值的时候,(Y,-,Y_fit)很小;次,假如参数的相之间相关性很小,这就使DD_Y_fit(j,,i)在i,,j相等的时候值很小甚至等0(参数之间相互正交)。再次,考虑到2和-2是常数,可以互相抵。于是,LM法用H’(i,,j)(几何值相于Hessen矩阵的一半)来代替Hessen矩阵,具体的
H’(i,,j)=,sum[D_Y_fit(i)*,D_Y_fit(j)],(i不等于j,时) H’(i,,i)=,(1,+,r),*,sum[D_Y_fit(i)*,D_Y_fit(i)]
假设D_A,=,(,A:min,-,A:current)是最佳参数和当前
LM法就是
1),假设一个r可以从1开始,解方程,D_A,*,H’,=,(-1/2)grad(L) 细心的同学已经发现了,这是一线性方程,意味着在matlab里面一步就可以
D_A,=,H’,\,((-1/2)grad(L))
没有
2),比较L(A:current,+,D_A,),和L(A:current,),这个时候
b),否则就增加,r(
3),重
这个方法可以有两个结束指a),r很大时,说明方程到了平坦区。b),每一次解方程以后,会比较一次L,如L还在减,但是减小幅度很小时,可以束。 际应用中,有用r小来结束,因为L变化的减小比r快。当然,r小也是一个结条件,只是,r还没有小时,L的变化已经很小了。说明拟合已经十分接近
有一点要注意,就是接近终点时计算Hessen矩阵(Newton,法)或者H’(,Levenberg-Marquardt法)的inv会得十分不稳定,就matlab说QR,decomposition,能出现错误。如果你用r=1e+20计算时,本上matlab,backslash,是得不到什么结果的。建议用函数inv()来计算。者用经过“最大绝对优先”的Gauss-Jordan法。他们
关于拟合的误差:
最小二乘的拟合可以用1/2Hessen矩阵来估计,Levenberg-Marquardt法中可以r=0的时候的H’的inv来计算。具体
A的无偏标差(覆盖68%的置信区间)=,+/-,sqrt(,L/(自由
这里,L就是用后得到的拟合参数计算的方差和,自由度的义是 自由,=,拟合样本数(x-y,
总结:
matlab计算非线性最小二乘方法大致
1),确定拟合函数F(,A,,X,),写出函数对各个参数的一介偏导数的函数D_Y_fit(1~n)(如果手算有困难,可以用Mathematica之类的支持符号运算软件帮忙,说也可以用matlab的符号运算工具箱,不过自己没有试过),如果偏导数较简单,还可以
2),
L,=,sum,((Y,-,F(,A,,X,),).^2) (least,square)
3),根据1)的函数,用上面的定义,用估计值A:current构建(-1/2)grad(L),矩阵G。第j个元素g'(j)可以由下面的方法得
g'(j)=,sum[(Y,-,Y_fit)*,D_Y_fit(j)] 和H’矩阵(Levenberg-Marquardt法):
H’(i,,j)=,sum[D_Y_fit(i)*,D_Y_fit(j)],(i不等于j,时)
H’(i,,i)=,(1,+,r),*,sum[D_Y_fit(i)*,D_Y_fit(i)]
或者1/2Hessen矩
H(i,,j)=,sum[D_Y_fit(i)*,D_Y_fit(j)-,(Y,-,Y_fit)*,DD_Y_fit(j,,i)]
因为A有,X,Y有了,所以上面矩阵都是
4)解方程
D_A=,H’,\,G,(LM法),或者,D_A=,H,\,G,(Newton,法)
用A:next,=,A:current,+,D_A,重新计算2)
注意,计算2)之前,可对A:next作一个范围检查,对于越过边界条件的值可以修正。方:i,),留原来的;ii,)用边条件;iii)对第j不合条件的值,取一个小的D_A(j)(
重
5),果是LM法,根据上面
a),L(A:next),<>
b),
如
a),L(A:next),<,l(a:current,),保留a:next,(a:current,=,a:next),>
通常,Newton,法结束
6),重复3)之前,可以用文
7),完结束了可以根据需要,求一误差。不
用matlab大致就是这样。
其实写这篇文章的时,正好在做关于非线性拟合的模型。发现matlab的fit不能给参数的误,就用以前的c++方法改一下,放在matlab里面。顺便总结了面的文字,当然,只是自己的理解,如果有什么不完整的,还希望大家
下次我会帖c++线性拟和的方法,主要是Levenberg-Marquardt方。大如果有比较棘手的函数需要拟和,不妨帖一个,看看是否可以作为例子,用c++
有任问题,也欢迎大家
freecat,2007-6-22,23:16
想问一下
确定
如果函数非性而且非常复杂,而且不能用一函数来描,也就是说F未
[[i],本帖
这个问非常好。其实自己也不是
通常的,如果没规律,且非线性。如果是拟合某一个连续的间,多项式合是可以的(类似原函数的
如果是连续的,那么就只
实在不行,还用"枚举",建立评价函数,利用计算机速度来解。
一般来说,不能100%的解决,还是可在一个比较
当然,体的方案还需视实际情
狐狸
建立评价函数,启发式的迭代优化方法求极值,是一个行之有效方法,虽然种法的收敛性质未必一定稳定,但确实可以在一个比较高的概率范围内解题
freecat,2007-6-23,23:58
[quote]原帖由,[i]recbio[/i],于,2007-6-23,22:13,发
表,[url=http://www.dolc.de/forum/redirect.php?goto=findpost&pid=83727
51&ptid=527435][img]http://www.dolc.de/forum/images/common/back.gif[/
img][/url]
这个问非常好。其实自己也不是
通常的,如果没规律,且非线性。如果是拟合某一个连续的间,多项式合是可以的(类似原函数的
...,[/quote]
我自己的文也是卡在了这里,对于一个谓评价函数
启发式迭求近似最优解,但是在函数和数的一一对
统的
工作文档matlab处理非线性误差估计
用matlab拟和模
Matlab用以建立数学模型是一个很好的工具。对模型数评价,一个很要的方法就最小二乘(Least squares)由least mean squares这个方法得到。假如点集P(X, Y),每个点 P(i) X(i), Y(i) , i = 1 ~ m组成;模 Y_fit = F( A, X ), Y_fit(i) = F(A, X(i) ); 其中 A= A(1) A(2) ? A(n)是
= 1 ~ m)。
一个好的模型,least mean squares就小;而另一方面,如何到模型参A,使得least mean squares有最小值,就是所谓的,最小二
简介:
模型有线性和非线性之。线性模型,求参数,其实就是求一步矩阵的逆(稍候我们可以看)。而非线模型,往不能一步就得结果,以就需多步逼。就这样,在众多的多步逼近的方法中,快收敛于最
A: n+1 = A: n + (Hessen ( L ))^-1 * grad(L)
这里Hessen ( L )是被拟合的模型函数的least mean squares方法的Hessen矩。grad(L)是她的梯度
这个方法包含了一个求hessen矩阵的逆运算。实,这个方法难的是这个逆,是如何得到Hessen矩阵和梯度矩阵。梯度矩阵还好说,就是least mean squares方法的对各参的一介偏导数。而Hessen矩阵包含了一介偏导的组合(主要是乘),和二介偏导。当然,许多型的二介偏导数相对于一导数的组合是一个比较小的量,特别是线性模型,就有二介偏导(所以,线性型可以直接求出参数)。于是,新的方就利用这个特,将逼近限制一介偏导数构成的伪Hessen矩阵上。这就诞生了两
Gauss-Newton 法和Levenberg-Marquardt法。
Gauss-Newton 接用Jacobian 行列式代替 Hessen矩阵,用least squares值代替梯度(注,不是least mean squares,因为当用Jacobian 行列代替Hessen矩阵时,中间有一个自由度的差别)这里的拟合
A: n+1 = A: n + (Jacobian ( L ))^-1 * L (对L的定义会在下文中给出)
因为越是接近最佳值(或者临界值),Jacobian ( L )就越是畸形,以在实际的计机运中,逆这一步都用所谓的帽子运
( Jacobian ( L ) )^-1 ---> ( ( Trans(J) * J )^-1) * Trans(J)
这里Trans()是转置运算。
Levenberg-Marquardt法比Gauss-Newton好,以说,在很多时,和Newton 法是一样的(当参数互相独立的时候,而这个条件是的数学模型基本的条,虽然有时候不100%保证,但是,基本上数互相之间相性大)。与Newton 相比,Levenberg-Marquardt法因为没有纯的二介偏导运,速度有时候还比Newton 法要快。而且,Levenberg-Marquardt法引入了一个步长,使得该方法在计算机运算上,
实现:
下面我们简说一下这个Levenberg-Marquardt法,
假设 L = sum ((Y - Y_fit ).^2) (Y= [Y (1), Y(2)? Y(m)]是测量值, Y_fit = F( A, X )=[ F( A(1), A(2)?A(n), X(1)), F( A(1), A(2)?A(n),
就是对X(2))?F( A(1), A(2)?A(n), X(m))] ), 是模值。其中的X(1)~(m)应于Y的测量值,A(1)~(n)是模型的参
使L最小的参数A就是我们要求的参数。L线时,L的最小值,就是要求足L对于各个数的偏导数=0的点(相当于解一个多元一次方程组)。当L非线性,上述的条件依然有,就是不能解。就有了逼近法。考虑到非性模型的二介数不全为零,如果给定一接近最佳参数值的估计参A:current,最佳参数(使得L最小
grad(L)是一个一维向量,第j个向量g(j)是L参数A(j)的
假设F( A, X )对A(j)的一介
g(j)= - 2 * sum[(Y - Y_fit)* D_Y_fit(j)] Hessen (L)是一个二维的矩阵,第i行第j列的值
H(i, j)=2*sum[D_Y_fit(i)* D_Y_fit(j)- (Y - Y_fit)* DD_Y_fit(j, i)]
这里DD_Y_fit(j, i)是模型函数F( A, X )先A(j)参数求一
在Levenberg-Marquardt法,先考虑到(Y - Y_fit)* DD_Y_fit(j, i)这一项,在接近最佳值的时候,(Y - Y_fit)很小;次,假如参数的之间相关性很小,这就使得DD_Y_fit(j, i)i, j不等的时候值很小甚至等于0(参数之间相互正交)。再次,考虑到2和-2是常数,可以互相抵消。于是,LM法用H’(i, j)(几何值相于Hessen矩阵的一半)来代替Hessen矩阵,具体的计
H’(i, j)= sum[D_Y_fit(i)* D_Y_fit(j)] (i不等于j 时)
H’(i, i)= (1 + r) * sum[D_Y_fit(i)* D_Y_fit(i)]
假设D_A = ( A:min - A:current)是最佳参数和当前
LM法就是
1) 假设一个r可以从1开始,解方程 D_A * H’ = (-1/2)grad(L) 细心的同学已经发现了,这是一线性方程,意味着在matlab里面一步就可以
D_A = H’ \ ((-1/2)grad(L))
没有
2) 比较L(A:current + D_A ) 和L(A:current ),这个时候
b) 否则就增加 r(
3) 重
这个方法可以有两个结束指a) r很大时,说明方程到了平坦区。b) 每一次解方程以后,会比较一次L,如L还在减,但是减小幅度很小时,可以束。 际应用中,有用r小来结束,因为L变化的减小比r快。当然,r小也是一个结条件,只是,r还没有小时,L的变化已经很小了。说明拟合已经十分接近
有一点要注意,就是接近终点时计算Hessen矩阵(Newton 法)或者H’( Levenberg-Marquardt法)的inv会得十分不稳定,就matlab说QR decomposition,能出现错误。如果你用r=1e+20计算时,本上matlab backslash 是得不到什么结果的。建议用函数inv()来计算。者用经过“最大绝对优先”的Gauss-Jordan法。他们
关于拟合的误差:
最小二乘的拟合可以用1/2Hessen矩阵来估计,Levenberg-Marquardt法中可以r=0的时候的H’的inv来计算。具体
A的无偏标准误差(覆68%的置信区间)= +/- sqrt( L/(自由度)* diag(H’^-1)) 这里,L就用最后得的拟参数计算的方差和,自由度的定义是
总结:
matlab计算非线性最小二乘方法大致
1) 确定拟合函数F( A, X ),写出函数对各个参数的一介偏导数的函数D_Y_fit(1~n)(如果手算有困难,可以用Mathematica之类的支持符号运算软件帮忙,说也可以用matlab的符号运算工具箱,不过自己没有试过),如果偏导数较简单,还可以
2) 用一组
square)
3) 根据1)的函数,用上面的定义,用估计值A:current构建(-1/2)grad(L) 矩阵G。第j个元素g'(j)可以由下面的方法
g'(j)= sum[(Y - Y_fit)* D_Y_fit(j)] 和H’矩阵(Levenberg-Marquardt法):
H’(i, j)= sum[D_Y_fit(i)* D_Y_fit(j)] (i不等于j 时) H’(i, i)= (1 + r) * sum[D_Y_fit(i)* D_Y_fit(i)]
或者1/2Hessen矩
H(i, j)= sum[D_Y_fit(i)* D_Y_fit(j)- (Y - Y_fit)* DD_Y_fit(j, i)]
因为A有,X Y有了,所以上面矩阵都是
4)解方程
D_A= H’ \ G (LM法) 或者 D_A= H \ G (Newton 法)
用A:next = A:current + D_A 重新计算2)
注意,计算2)之前,可以A:next作一个范围检查,对于越过边界条件的值可以修正。方法:i ) 保留原来值;ii )用边界条件;iii)对第j个不条件的,取一个小的D_A(j)(比如A:next(j) = A:current(i) + D_A(i)/10 , 重复直到满足
5) 果是LM法,根据上面
a) L(A:next) < l(a:current="">
b)
如
a) L(A:next) < l(a:current="" ),保留a:next="" (a:current="A:next)," b)="">
通常,Newton 法结束
6) 重复3)之前,可以用文
7) 完结束了可以根据需要,求一误差。不
用matlab大致就是这样。
其实写这篇文章的时,正好在做关于非线性拟合的模型。发现matlab的fit不能给参数的误,就用以前的c++方法改一下,放在matlab里面。顺便总结了面的文字,当然,只是自己的理解,如果有什么不完整的,还希望大家
下次我会帖c++线性拟和的方法,主要是Levenberg-Marquardt方。大如果有比较棘手的函数需要拟和,不妨帖一个,看看是否可以作为例子,用c++
有任何问题,也欢迎大家回帖或者给自己
想问一下
确定
如果函数非性而且非常复杂,而且不能用一函数来描,也就是说F未
[[i] 本帖
这个问非常好。其实自己也不是
通常的,如果没规律,且非线性。如果是拟合某一个连续的间,多项式合是可以的(类似原函数的
如果是连续的,那么就只
实在不行,还用"枚举",建立评价函数,利用计算机速度来解。
一般来说,不能100%的解决,还是可在一个比较
当然,具体的案还需视实
狐狸老大 2007-6-23 23:39
建立评价函数,后用启发的迭代优方法求极值,一个行之有效的方法,这种方法的收敛性质未必一定稳定,但确实可以在一个较高的
freecat 2007-6-23 23:58
[quote]原帖由 [i]recbio[/i] 于 2007-6-23 22:13 发表
[url=http://www.dolc.de/forum/redirect.php?goto=findpost&pid=8372751&
ptid=527435][img]http://www.dolc.de/forum/images/common/back.gif[/img
][/url]
这个问题非常。其实自己也
通常的,如果没有规律,且非线性。如果是拟合一个连续的区间,多拟合总是可以的(类似原函数的泰勒展开)。就是数的意
... [/quote]
我自己的论文也是卡在了这,对于一个所评价函数的求,倒可以用所谓启发式求近似最优解,但是在函数和参数的一一对应关系不明确之前,传统的梯
matlab非线性拟合
设有实验数据 ( xi , y i ), (i = 1,2,? , n) ,寻找函数
f ( x,θ )
使得函数在点 xi , (i = 1,2,?, n) 处的函数值与观据偏差 ?) 使得 f ( x,θ 的平方和达到小.即
?) ? y ) 2 min∑ ( f ( xi , θ ) ? y i ) = ∑ ( f ( xi , θ i
2 i =1 i =1 n n
其中θ 是待定的参数,而 θ? 就是最小法所确定的 最佳数. 解决此类问题有以几个步骤:(1)首先作出散点 图,确数类别;(2)据已知数据确定待定 参数的初始值,利用Matlab软件计算最佳参数;(3) 据可决系数,比拟合效果,计算可决系数
R2 = 1 ?
1 n y = ∑ yi n i =1
2 ? ( y y ) ? ∑ i i i =1 n
n
∑(y
i =1
i
? y) 2
其中
R2越趋近于1
在Matlab中实
x=[2:16]; y=[6.42,8.2,9.58,9.5,9.7,10,9.93,9.99,10.49,10.59,10.6,10.8,10.6,10.9,10.76];
y1=x./(0.1152+0.0845*x); % 拟合曲线
R2=1-sum((y-y1).^2)/sum((y-mean(y)).^2) 果是多式函数,则称为多项式回归,时 的参数即多项的系数;如果为指数函数、对数函 数、幂函数或三角函数等,则称为非线性拟.下面 的图形出了常见曲线与方程的对
幂函数
y = ax b
指数函数 y = ae bx
双曲线函数
y=
x ax + b
对数函数
y = a + b ln x
指数函数
y = ae
b x
S形曲线
y=
1 a + be ? x
具有S形曲线的
:
y=
α 1 + β e ?γ x
龚帕兹(Gomperty)模型: 理查德(Richards)模型: 威布尔(Weibull)模型:
y = α exp(? βe ? kx )
y = α /[1 + exp( β ? γ x)]1 / δ
y = α ? β exp(?γ t δ )
为了实现非线性拟合,首先要义在线函数 1. inline 定义函数:用于曲线拟合、数计算 步
? cx ( 1 be ) a,b,c待定的参数 y a = ?
fun=inline('b(1)*(1-b(2)*exp(-b(3)*x))','b','x'); 此处,将b看成参变量,b(1),b(2),b(3)其分量. 若计算函数在x=0:0.1:1上的函数值,由于此时x为矩阵, 只需将数表达式中的某
在实际问题中,有时散点图作出后未必是多项式的 图形,像他的曲线,这时可以猜测线类型, 然后利用如下命令: [beta,r,J] = nlinfit(x,y,fun,beta0) 其中,x,y为始数据,fun是M文件定义的函数, beta0是函数中参数的初始值;beta为参数的最优值,r 是各点的拟残差,J为雅克比
k=[ 0,47,93,140,186,279,372,465,558,651]; y=[18.98,27.35,34.86,38.52,38.44,37.73,38.43,43.87,42.77,46.22];
plot(k,y,'*')
根据右图,
y = b1 (1 - b 2e - b 3 k )
现在利用最小乘法确定
b0=[43,0.6,
0.1]; %初始参数值 fun=inline('b(1)*(1-b(2)*exp(-b(3)*k))','b','k'); [b,r,j]=nlinfit(k,y,fun,b0); b %最佳参
(图6.3)
拟合结果如右图 示,红色为拟 曲线图形,*为 原始散点图.
50 45 40 35 30 25 20 15 0 100 200 300 400 500 600 700
(图6.4) y1=42.6643*(1-0.5483*exp(-0.0099*k)); plot(k,y,'*',k,y1,'-or') 练习:计算可决系数
例3.炼钢厂出钢时所用盛水的钢包,由钢水对耐 火材的侵,容积不断增大,希望找出使用次 数与增大容积之间的函数关系.实验数据如下: 表4.2
使用 次数 增大 容积 使用 次数 增大
10.49 10.59 10.6 10.8 10.6 10.9 10.76
x y = 分别
y = a(1 + be )
cx
y = ae
b x
拟合钢包容积与用次数的关系 ,在同一坐标系内 作出
下面给出分式函数拟合程序: x1=[2:16]; y1=[6.42,8.2,9.58,9.5,9.7,10,9.93,9.99,10.49,10.59,10.6,10.8 ,10.6,10.9,10.76]; b01=[0.1435,0.084]; %初始参数值 fun1=inline('x./(b(1)+b(2)*x)','b','x'); % 定义函数 [b1,r1,j1]=nlinfit(x1,y1,fun1,b01); y=x1./(0.1152+0.0845*x1); %根据b1写出具体函数 plot(x1,y1,'*',x1,y,'-or'); 可决系数计算: 初始数b0的算, 由于确定两个参数值,因此我 们选择已知数据中的两点(2,6.42)和(16,10.76)代 方程,得到方程
2 ? 6 . 42 = ? 2a + b ? 16 ?10.76 = 16a + b ?
? 6.42(2a + b) = 2 ? a = 0.084 ?? ?? ?10.76 (16a + b) = 16 ?b = 0.1435
上述方程组有两种解法:手工,Matlab,下面介 绍Matlab 解方程组的方法 [x,y]=solve('6.42*(2*a+b)=2','10.76*(16*a+b)=16')
y = a (1 + be ) ?
cx
ln b + cx = ln( y / a ? 1)
取点:(2,6.42),(8,9.93),(10,10.49)
[a,b,c]=solve('log(b)+c*2=log(6.42/a-1)','log(b)+c*10=log(10.49/a-1)','log(b)+c*8=log(9.93/a-1)')
注意:如果出现
matlab非线性规划
开课学院、实验室: 实验时间 : 年 月 日
实验项目类型
验证 演示
指导 成 绩
教师
实验目的
[1] 学习线性规划
[2] 掌握立非线性规
[3] 熟悉MATLAB软求解非线性规划模型的基
[4] 通过范例学,了解建立非线性划模型的全过程,与线性规划比其
基础实验一
一、实验内容
1求解无约束优化
22,,0.20.5()xx0.5(cos(2)cos(2)),,xx,1212min(,)2022.713fxxee,,,,12
stxi..55,1,2,,,,i
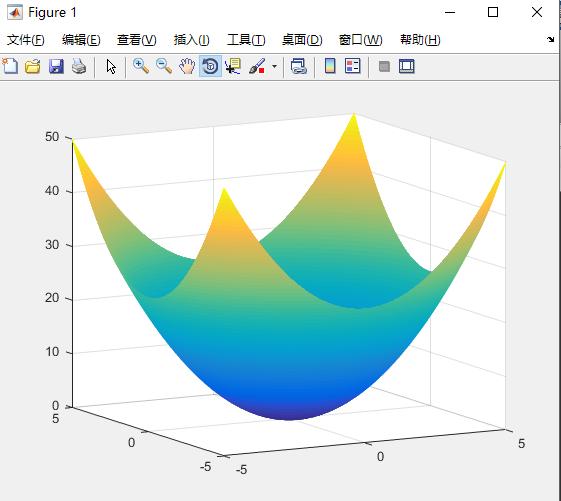
1) 画出该面图形,
2) 使用fminunc命
二、实验过程
(1)作图
1)由于命令surf函数在使用过中不能出现复合的变量表示形式,因而
x1->X,x2->Y,Z=f(x1,x2);
2)输
x=-5:0.01:5;
y=-5:0.01:5;
[X,Y]=meshgrid(x,y);
Z=-20.*exp(-0.2.*(0.5.*(X.^2+Y.^2).^0.5))-exp(0.5.*(cos(2.*pi.*X)+cos(2.*pi
.*Y)))+22.713;
surf(X,Y,Z)
shading flat
3)输出结果:
(2)使用fminunc命令求解
1)建立M文件
function f=fun1(x)
f=-20*exp(-0.2*(0.5*x(1).^2+0.5*x(2).^2).^0.5)-exp(0.5*(cos(2*pi*x(1))+cos(2*pi*x(2))))+22
.713;
2)matlab命令
[x,fval]=fminunc('fun1',[0,0],1)
3)输出结果
x =
0 0
fval =
-0.0053
基础实验二
一、实验内容
求解非线性规,试判定你所求到的解是
420.201xxx123maxz,710
2stxx..6750,,12
22xx130.4190,,710
036,05,0125,,,,,,xxx123
二、实验过程
(1)目标函数以
min z=-0.201.*x1^4.*x2.*x3^2.*10^(-7)
s.t. -675+x1^2.*x2<=0>
-0.419+x1^2.*x3^2<=0>
0<><><><><><=125>
(2)编写,文件
?function f=mf1(x)
f=-0.201.*x1^4.*x2.*x3^2.*10^(-7);
?function [G,Geq]=cont2(x)
G(1)=-675+x1^2.*x2;
G(2)= -0.419+x1^2.*x3^2
Geq=[];
(3)输入程序:
Aeq=[];
b=[];
beq=[];
A=[];
lb=[0,0,0];
ub=[36,5,125];
x0=[1,1,1];
[x,fval]=fmincon('mf1',x0,A,b,Aeq,beq,lb,ub,'cont2')
(4)运行结果:
x =
1 1 1
fval =
-2.0100e-008
应用实验
一、实验内容
组合投资问题
设有8种投资选择:5股票,2种债券,黄金. 投资者收集到这些投资项目的年益
(见表6.1), 投者应如何分配他的投资金,即需要确定这8种投资的最投资
表6.1 8种投
项目 债券1 债2 股票1
年份
1973 1.075 0.942 0.852 0.815 0.698 1.023 0.851 1.677
1974 1.084 1.020 0.735 0.716 0.662 1.002 0.768 1.722
1975 1.061 1.056 1.371 1.385 1.318 1.123 1.354 0.760
1976 1.052 1.175 1.236 1.266 1.280 1.156 1.025 0.960
1977 1.055 1.002 0.926 0.974 1.093 1.030 1.181 1.200
1978 1.077 0.982 1.064 1.093 1.146 1.012 1.326 1.295
1979 1.109 0.978 1.184 1.256 1.307 1.023 1.048 2.212
1980 1.127 0.947 1.323 1.337 1.367 1.031 1.226 1.296
1981 1.156 1.003 0.949 0.963 0.990 1.073 0.977 0.688
1982 1.117 1.465 1.215 1.187 1.213 1.311 0.981 1.084
1983 1.092 0.985 1.224 1.235 1.217 1.080 1.237 0.872
1984 1.103 1.159 1.061 1.030 0.903 1.150 1.074 0.825
1985 1.080 1.366 1.316 1.326 1.333 1.213 1.562 1.006
1986 1.063 1.309 1.186 1.161 1.086 1.156 1.694 1.216
1987 1.061 0.925 1.052 1.023 0.959 1.023 1.246 1.244
1988 1.071 1.086 1.165 1.179 1.165 1.076 1.283 0.861
1989 1.087 1.212 1.316 1.292 1.204 1.142 1.105 0.977
1990 1.080 1.054 0.968 0.938 0.830 1.083 0.766 0.922
1991 1.057 1.193 1.304 1.342 1.594 1.161 1.121 0.958
1992 1.036 1.079 1.076 1.090 1.174 1.076 0.878 0.926
1993 1.031 1.217 1.100 1.113 1.162 1.110 1.326 1.146
1994 1.045 0.889 1.012 0.999 0.968 0.965 1.078 0.990
二、问题分析
设投资的限是一年,不妨设投资数为1个单位,用于第i项投资的金比
X=(x1,x2,…,xn)称为投组合向量.
T
种投资的平
k,1
收益的波动程,可用样本
T 2qrrT,,(())/,jjkj ,1k
投资组合X=(x1,x2,…,xn) 的平均收益率为:
TT8 11RXRXxr,,()(),,,kjjk TT,,,kkj111
投资组合X=(x1,x2,…,xn)的风险为:
2TT8 ,,112QXRXRX,,()[()()]xrr,,,,,k,,,,jjkjT T,1k,,kj11,,
三、
利用双目标函数,利润最大化,风险最小化,进行
RX(),, max,,,QX(),,
s.t. x1+x2+…+x8=1,
xi>=0, i=1,2,…,8
线性
max(1)()(),,,,,RXQX
stxxx..1,,,,12n
xin,,01,2,,i
模型
R=xlsread('tz.xlsx');
0,,,1
[shouyi,fengxian]=tzzh(R)
plot(shouyi,fengxian,'r'),hold on, plot(shouyi,fengxian,'k*'),hold off,grid
0.06
0.05
0.04
0.03
年投资总
0.01
01.081.091.11.111.121.131.141.151.16
四、实
随着年益率的增加,年投资总险也逐渐成指数增加,这符号实际情,因
可靠的。投资者以根据自己的实风险承受能力,选择相应的
五、附录
function [shouyi,fengxian]=tzzh( R )
junzhi=zeros(1,8);
for i=1:8
junzhi(i)=mean(R(:,i)); end
A1=[];b1=[];
A2=ones(1,8);b2=1;v1=zeros(1,8); h=zeros(8,8);
for i=1:8
for j=1:8
xfz=cov(R(:,i),R(:,j));
h(i,j)=xfz(1,2);
p(i,j)=h(i,j);
if i==j
h(i,j)=2*h(i,j);
end
end
end
for t=1:11
n=(t-1)/10;
c=(n-1)*junzhi;
H=n*h;
[x,fv,ef]=quadprog(H,c,A1,b1,A2,b2,v1)
Shouyi(t)=sum(x'.*junzhi)
Fengxian(t)=sum(sum(x*x'.*p))
End
end
总结与体会
做这三个实验,我都遇到一定的困难,尤其是第三个应验,在同学的协助下才完成,而且并未完全掌握,以后
教师签名
年 月 日
转载请注明出处范文大全网 » matlab求非线性误差matlab处理非线性误差估计



 嗫?暁雲?
嗫?暁雲?

