1. 卷积
1.1卷积的
1.2互相
1.3卷积
2. 卷积
2.1卷积
2.2相关
3. 卷积
3.1卷积运算和相关运算的展宽效
3.2卷积
3.3相关
卷积和相关的区别
1. 卷积和
1.1卷积的定义
设函数f(x) 、g(x) 是R的两个可积函数,
F x = ?∞f ξ g(x?ξ) dξ ①
则称 (x) 为函数f(x) 与g(x) 的卷积。常表示为F x =f x ?g(x) .
卷积是频率分析的一种工具,其与傅变换有着密切系。利用一点质,即两数的傅立叶变换乘积等于它们乘积后的傅立叶变换,能傅立叶分析中许多
1.2互相关
设函数f(x) 、g(x) 是R的两个可积函数,
Gfg x = ?∞f η g(η+x) dη ②
则称G(x) 为函数f(x) g(x) 的互相
(容易证明Gfg x = ?∞f η g(η+x) dη与Gfg x = ?∞f η g(η?x) dη等价)。
互相关函数描述了两信号之间的相情或取值依赖关系。如果对一理想测试统的输入和输出号求互相关函数,那么,互相关函数得最大值的x值
1.3卷积和相
比较①式和②
1)在①式中被积函的第二个因子g(x?ξ) 如果ξ不反号,便成为相关
+∞+∞+∞+∞
2)当函数g(x) 为偶函数时,积运算与相关运算完
2. 卷积与相
2.1卷积
设f(x) 为矩形脉信号,g(x) 为三角脉冲信号,如图1(a)所示。则卷积的运
(c)
图1 卷积的运算过程 (a) (b) (d)
图1表示首先将g(ξ) 对折(即反号),得到g(?ξ) ,平x个单得到g(x?ξ) ,然后将g(x?ξ) 另一数f(ξ) 相乘后从?∞到+∞积分(对ξ分),得到相乘后的新曲f(ξ) ?g(x?ξ) 与横坐标轴包围的积S(如图1 (d)),该积S便是f(ξ) 与g(ξ) 在x点处的卷积。取不同的x值时,
可见卷积可分为对折、平移、积分三步。
2.2相关
相关的运算过程与卷积的运程相似,但不对折(即反射标)。直接将g(ξ) 平移到x点与f(ξ) 相乘后积
对于卷积运算和相关运算的运算规律区别,此处不再一
3. 卷积与相
3.1卷积运算和相
从前面卷积与相运的过程我们可以看到,当g(ξ) 移动f(ξ) 的边界,两个函数仍有重叠部分,仍在积(或关)。只有当g(ξ) 移动到f(ξ) 边界以外达到g(ξ) 宽度时,两个数才无重合部分,此时两个函的卷积(或相关)才为零。可见两个函数f(ξ) 和g(ξ) 进行卷积运算(或相关运算)
3.2卷积运算
卷积运算中g(ξ) 反射坐标后平移x时两个函数重合分之点积与横坐轴所包围面积作为卷积的值,值是两个函数在x点出重合部分的总体效应,从而将两个函数在x点
3.3相关
相关运算中的g(ξ) 不反射坐标,直接平到x点对另一数f(ξ) 头到尾进行扫描。反映的是求个函f(ξ) 与g(ξ) 的相似程度。当f ξ =g(ξ) 时,反映的是自与自己的相似程度,此时又称为自相关运算。当自相关运算扫描到完全重合,相似程度达到最大,产生一个峰值。这
实验二相关与卷积
实验二、卷积与相关
【实验目的及要求】
1、掌握快速傅立叶
2、掌握利用快速傅立叶换实现快速
3、掌握利用快速傅立
【实验仪器】
电脑、Matlab 软件。
【实验原理】
1、快速傅立叶
语法格式:F=fft2(f ) ;其中,F 与f 的大一致。运算速度取决
注意:为了图像的傅立叶变换,在用imshow(.)或mesh(.)命显示之,要对变换后结果用命令abs(.)求绝对值,除此之,为了能正确显示,还要分别用命令fftshift(.)和mat2gray(.)对
2、卷积定理
f (x , y ) ﹡h (x , y ) F (u , v ) H(u , v )
根据卷积定理,要求两个数的卷积,可以求出两函数的傅叶变换,然后相乘,最后对乘积作
注意:在利用快速傅立叶变换计算积,为了避免相邻周期之间干扰,必要在傅立叶变换前对原图像进行零填充。假设f (x , y ) 的
h (x , y ) 的小p ×q ,则要把参卷积的两个
例:
3、相关定理
f (x , y ) ★h (x , y ) ? F *(u , v ) H (u , v )
根据相关理,要两函数的相关,可以先求出两个函的傅立叶变换,然其中一个共轭并另一个相乘,最后对乘积作傅立叶变换。 意:在利用快速傅立叶变计算相关时,同样为了避免邻周期之间的干扰,必须要傅立叶变换前原图像进行零填充。假设f (x , y ) 的大小为m ×n ,h (x , y ) 的大小p ×q ,则需要把参与相关的两个图像的
例:
【实验内容】
1、对一图像进傅立叶变换和逆变换,并查看其频谱和逆
2、求出任意两
3、求出任意一幅图像的自相和两幅图像的
【实验数据记录】
1、记录各项实
2、记录各项实验
【思考题】
1、为什么查看傅立
2、imshow
3、利用快速傅立叶变换求积时为什么要
MATLAB仿真,相关函数和卷积的应用信号与系统
一、相关函
1、自相关函数的
自相关函数具有
(1) R(x)为实函数;
(2) R(x)为偶函数,即R(x)=R(-x);
(3) R(0)等
(4) 对于各态经性的随机信号s(t)有R(x)在R(0)处取得
2limR(x),u(5) 当随机信s(t)的均值u时,有,当s(t)为确定性信
当x??时,自相关函数不为均值的
(6) 若平稳随机号s(t)有周期成分,它的自相关函数R(x)
成分,且R(x)中的周期成分的周期与号s(t)中的周期成
自相关函数
(1) 从被噪声扰的信号中找出周期成分,
2、互相关函数的
互相关函数的性质
(1) 互相关函数R(τ )是实
(2) 对于任意τ,R(τ )的平方小
(3) 若信号是零均值的,在τ??时,相关函数值趋
R(τ )R(-τ )(4) 互相关函
R(τ )(5) 若个信号x(t)与y(t)均有周期分量,且周期相等,则互
也含有相同周期的
互相关函数的应用
例:带白噪声干扰频率为10Hz的正弦号和不带白噪声的信号的
clf;N=1000;Fs=500;
n=0:N-1;t=n/Fs;
Lag=100;
randn('state',0);
x=sin(2*pi*10*t);
[c,lags]=xcorr(x,Lag,'unbiased'); subplot(2,2,1),plot(t,x);
xlabel('时间/s');ylabel('x(t)'); title('不带噪声周
grid on;
subplot(2,2,2),plot(lags/Fs,c); xlabel('时间/s');ylabel('Rx(t)'); title('不带噪
y=sin(2*pi*10*t)+0.6*randn(1,length(t));
[c,lags]=xcorr(y,Lag,'unbiased'); subplot(2,2,3),plot(t,y);
xlabel('时间/s');ylabel('y(t)'); title('带噪声周期
grid on;
subplot(2,2,4),plot(lags/Fs,c); xlabel('时间/s');ylabel('Ry(t)'); title('带
带白噪声正弦信号察不信号的周期,通过求其自相关函数可以被噪声干扰的信中找周期成分。在用噪声断机器运行状态时,正常机器噪声由大量、无序、大小近相等的随机成分叠加的结果,正常机器噪声具有较宽而均匀频谱。当机器状态异常时,随机噪将出现有规则、周性的信号,其幅度要比正常噪声的幅度大很多。用噪声诊断机器故障时,依靠自相关函就可噪声中发现隐藏的周期量,确定机器的缺陷所在。特别是对于早期故障,周期信号
二、卷积的应用
f(t)f(t)121、 成与两函数的卷
2,tf(t)f(t)f(t),eu(t),f(t),u(t),u(t,4)1212其中:一个图形窗口中,画出、以及卷积结果。要求每个坐标系有
p = 0.0001; %定义
%定
f1=exp(-2*t).*u(t); %将f(t)表示出来 f2=u(t)-u(t-4);
f=conv(f1,f2);
subplot(1,2,1);
plot(t,f1,t,f2); title('f1=e^-2t*u(t)'' / ''f2=u(t)-u(t-4)');
xlabel('t(sec)'); % 这行代码是给出x坐标的标签 ylabel('f(t)');
grid on;
subplot(1,2,2);
plot(f); title('f=f1*f2');
xlabel('t(sec)'); % 这行代码是给出x坐标的标签 ylabel('f')
grid on
线性卷积与圆周卷积的计算
1.实验目的
1) 通过编程,上机调试程序,进一步强使用计算机解决问题
2) 掌握线性卷积圆周卷积软件现的方法,
线性卷积;圆周卷积;个有限长序列的性卷积;圆周卷与线性卷积的关系。 3.实验
已知两个有
X(n)= δ(n)+2δ(n-1)+3δ(n-2)+4δ(n-3)+5δ(n-4)
h(n)= δ(n)+2δ(n-1)+δ(n-2)+2δ(n-3)
1.编制一个计两个线性卷积的通用程
2.编制一个计算圆周卷积的程序,计算上述4种情下两个列x(n)与h(n)的圆周卷积。 3.上机调试并打印或
4.将实验结果与预先笔算的果比较,验证真
4.相应程
1)编制一个算两个序列线性卷积的通
clear all;
xn=[1 2 3 4 5];
hn=[1 2 1 2];
yln=conv(xn,hn);
ny=[0:1:length(yln)-1];
stem(ny,yln);
xlabel('时
ylabel('
title('
2)编制一个计算圆周积的通用程序,计算上述4种
积。
主程序:
clear all
clc
N=[5 6 9 10];%圆周卷积的长
xn=[1 2 3 4 5];
hn=[1 2 1 2];
y1n=conv(xn,hn)%计算线
ny1=0:length(y1n)-1;%分别
yc1=circonv(xn,hn,N(1)) yc2=circonv(xn,hn,N(2)) yc3=circonv(xn,hn,N(3)) yc4=circonv(xn,hn,N(4))%分别作出线性卷积和取不
subplot(1,2,1)
stem(ny1,y1n);
xlabel('时
ylabel('
title('线
subplot(1,2,2)
stem(0:N(1)-1,yc1); xlabel('时间序号n');
ylabel('
title('5
figure
subplot(1,2,1)
stem(ny1,y1n);
xlabel('时
ylabel('
title('线
subplot(1,2,2)
stem(0:N(2)-1,yc2); xlabel('时间序号n');
ylabel('
title('6点
figure
subplot(1,2,1)
stem(ny1,y1n);
xlabel('时
ylabel('
title('线
subplot(1,2,2)
stem(0:N(3)-1,yc3); xlabel('时间序号n');
ylabel('
title('9点
figure
subplot(1,2,1)
stem(ny1,y1n);
xlabel('时
ylabel('
title('线
subplot(1,2,2)
stem(0:N(4)-1,yc4); xlabel('时间序号n');
ylabel('
title('10
2.圆周卷
function yc=circonv(x1,x2,N)
if length(x1)>N
error('N必须大于等
if length(x2)>N
error('N必须大于等
x1=[x1,zeros(1,N-length(x1))];
x2=[x2,zeros(1,N-length(x2))];
n=[0:N-1];
x2=x2(mod(-n,N)+1);
H=zeros(N,N);
for n=1:1:N
H(n,:)=cirshiftd(x2,n-1,N); end
yc=x1*H';
3.实现圆周
function y=cirshiftd(x,m,N) if length(x)>N
error('x的
end
x=[x,zeros(1,N-length(x))];
n=[0:1:N-1];
y=x(mod(n-m,N)+1);
5.思考题
1)线性卷积的运算骤一般可分哪几个部分,周卷积的运算步骤一般可
分,比较两者之
线性卷积:翻转,移
圆周卷积:翻转,移位,相,相加,取
2)采用圆周卷积运算代替性卷积运算的
运算量小。
循环卷积与线性卷积的实现
实验五 循环卷积与线性卷积
一、实验目的
(1) 进一步理解并掌握循环卷积线性卷积的概; (2) 理掌握二
二、实验原理
两个序列的N 点的循环卷积
[h (n ) ?x (n )]N =∑h (m ) x ((n -m )) N (0≤n
k =0N -1
从定义中可以看到,循环卷积和线卷积的不同之
卷积结仍为N 点序列,而它们的线卷积的结果长度则为2N -1;循环卷积序列的移位采取循环移位,而线性卷积序列采取线性位。正是这些不同,导致线性卷积和循环卷积有同的
两个序列的N 点循环卷积是它们的线性卷积以N 为周的周期延拓。设序列h (n ) 的长度N 1,序列x (n ) 的长度为N 2,此时线性卷积结果的序列点为N ' =N 1+N 2-1;因此如果循环卷积点数N 小于N 1+N 2-1,那么上述性延拓的结就会产生混叠,从两种卷积会有不同的结果。而如果足N =N ' 的条件,就有循环积与线性卷
根据DFT 循环卷积性质中的卷
DFT {[h (n ) ?x (n )]N }=DFT [x (n )]?DFT [h (n )]
因此可以根据性质先分别求两个序列的N 点DFT ,并乘,然后取IDFT 以得到
三、实验分析
例题:已知有限长序列x (n ) 与h (n ) 如下所示, (1) 画出两者间的线性卷 (2) 8点
解析如下:
(1)x (n ) 与h (n ) 的线性卷积,由公
h (n )*x (n ) =
m =-∞
∑x (m ) h (n -m )
∞
x (m ) 与h (-m ) 的图形
利用方格平移法:
由方格平移法可知: 当n =0时,h (n )*x (n ) =0 当n =1时,h (n )*x (n ) =0
当n =2时,h (n )*x (n ) =0*1+1*1=1 当n =3时,h (n )*x (n ) =2*1+1*1+0*1=3 当n =4时,h (n )*x (n ) =3*1+2*1+1*1+0*1=6 当n =5时,h (n )*x (n ) =3*1+2*1+1*1+0*1=6 当n =6,h (n )*x (n ) =3*1+2*1+1*1=6 当n =7时,h (n )*x (n ) =3*1+2*1=5 当n =8
得到图形如下:
(2)x (n ) 与h (n ) 8点圆卷积,由公
x (n ) ?h (n ) =∑x ((m )) 8h ((n -m )) 8G 8(n )
n =0
7
x ((m )) 8与h ((-m )) 8的图
根据下面图表可计算得到圆
取和得到圆卷积为3。
当n =2时: 取和得到圆卷积
取和得到圆卷积为6。
n =5取和得到圆卷积
取和得到圆卷积为6。
n =7取和得到圆卷积
得到波形如下:
(2)x (n ) 与h (n ) 5点圆卷积,由公
x (n ) ?h (n ) =∑x ((m )) 4h ((n -m )) 4G 4(n )
n =0
4
x ((m )) 4与h ((-m )) 4的图
根据图标可计算得到圆卷积: 当n =
0取和得到圆卷积为6。
当n =1时:
取和得到圆卷积为6。
当n =
2
当n =
3取和得到圆卷积为6。
当n =
4
画出波形如下:
四、仿真实验
Matlab 程序设计
编写的循环卷积程
方法一:直接根据定义计,程序编辑
function y=circonv1(x1,x2,N) if length(x1)>N
error('N must not be less than length of x1') end
if length(x2)>N
error('N must not be less than length of x2') end
x1=[x1,zeros(1,N-length(x1))]; x2=[x2,zeros(1,N-length(x2))]; n=[0:1:N-1];
x2=x2(mod(-n,N)+1); H=zeros(N,N); for n=1:1:N
H(n,:)=cd(x2,n-1,N); end
y=x1*H';
function y=cd(x,m,N) if length(x)>N error end
x=[x zeros(1,N-length(x))]; n=[0:1:N-1]; n=mod(n-m,N); y=x(n+1);
方法二:根据性质先分别求两个序列的N 点DFT ,相乘,然后取IDFT 以得
function y=circonv2(x1,x2,N) if length(x1)>N error('N must not be less than length of x1') end
if length(x2)>N error('N must not be less than length of x2') end
X1k=fft(x1,N); X2k=fft(x2,N);
Yk=X1k.*X2k; y=ifft(Yk);
if((all(imag(x1)==0))&&(all(imag(x2)==0))) y=real(y); end
编写的主程序:
n=[0:1:4];m=[0:1:4];
N1=length(n);N2=length(m); xn=ones(1,5); hn=[0,0,1,2,3]; y1n=conv(xn,hn);
y2n=circonv2(xn,hn,N1+N2-1); y3n=circonv1(xn,hn,N1); ny1=[0:1:length(y1n)-1]; ny2=[0:1:length(y3n)-1]; subplot(3,1,1); stem(ny1,y1n); subplot(3,1,2); stem(ny1,y2n); subplot(3,1,3); stem(ny2,y3n);
运行结果如下:
图表 1实验结果
与理论结果一致。
五、实验小结
通过本次实理解并掌握了循环卷积与线性卷积的概,也掌握了两者之的关系。学会了matlab 中线性卷积函数,以及如何编循环卷积。在仿真过程中出了一些问题,由于matlab 提供线性卷积函数,则只需要自己编写循环积,在编写过程,没有注意到matlab 中大小写的严格区别,导致程序运错误。经过反复检查之后发现了错,经改正得到了正确运
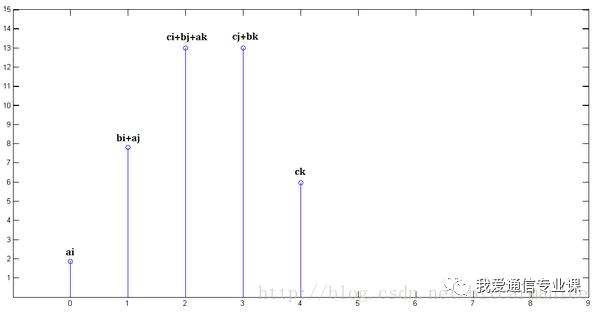
转载请注明出处范文大全网 » 卷积和相关的部分区别



 裤子挂钩
裤子挂钩

