数电分析原理
Feng建湖~电电明~电玉峰电著科出版社出版学
Suo电,号51.81/9电藏,号022623
内容介电:
Ben电系电地介电了电代科工程电算中常用的电Dian算方法及有电的理电和电用。全电共分学与Shu章~9
Bao括电差分析~函电~函逼近~电电分电微分、电性方程电的直接解法和迭代解法~数插数Shu与数非电性方程的电解法~矩电特征电特征Xiang量的电算~以及常微分方程初电电电的电解Fa等。本电数与数
Ji本念准~理电分析科电电~电言述通俗易~Dian电排由入深~注重电性。本电概清晰确学叙Dong构浅启始电电穿一基本理念~在理电上等价De方法在电电电电算电往往是不等效的~因此~本电个即数学数
Jing电了大量的电算电例~用电明各电电方法的Dian劣特点。各章末电有一定量的电电供电者电Dian之来数与数
用。
Dian者电象,高等院校工科究生和系各电电本科Sheng~事科工程电算的科工作者研数学从学与研。
本电目电:
第一章 电电
Shu与电分析的电象任电1?1
电差基电知电1?2
She入电差分析及电电定性数1?3
电电1
第二章 函电数插
插电电电2?1
Cha构电多电式的造方法2?2
分段电法插2?3
电电2
第三章 函逼近数
Dian范电性空电函逼近电电与数3?1
Nei与电空电正交多电式3?2
Zui佳平方逼近电与广电数3?3Fourier
Qu电电合的最小二乘方法3?4
Zui佳一致逼近多电式*3?5
电电3
Di四章 电电分电微分数与数
数概电电分述4?1
Niu电柯特斯公式4?2-
Dian电格求电算法4.3
Gao斯型求电公式4.4
Qi电分振电函电分的电算异与数*4?5
Er重电分的电算*4?6
数电微分4?7
电电4
Di五章 解电性代方程电的直接法数
高斯消去法5?1
Ju电三角分解法5?2
电路工具分析
Ju电的件和方程电的性电条数5?3
电电5
Di六章 解电性代方程电的迭代法数
Xiang量和矩电序列的限极6?1
Die代法的基本理电6?2
Ji电常用的迭代法6?3
Zui速下降法共电梯度法与*6?4
电电6
Di七章 非电性方程求根
二分法7?1
Die代法的算法和理电7?2
Die代的加速收电方法7?3
牛电迭代法7?4
Xian割法和抛物电法7?5
Fei电性方程电的迭代解法电介*7?6
电电7
Di八章 矩电特征电特征向量电算与
Cheng电法反电法与8?1
雅可比方法8?2
方法8?3QR
Qiu电电三电角电特征电的二分法称8?4
电电8
Di九章 常微分方程初电电电的电解法数
引言9?1
欧拉方法9?2
Dian格电塔方法9?3-
Dian步法的电一步电电9?4
电性多步方法9?5
Dian性多步法的电一步电电*9?6
Yi电方程电电性电电电介与9?7
电电9
参献考文
Fu电 电于电性常系差分方程的点知电数几
参考答案
58w__数值分析原理第六章
Ben利用函数的插值理论,构造了相应的数值微Fen与数值积分计算公式,并通过Richardson
(理查森)外推技巧提高了这些公式的计算精Du;另外,本章还对所建立公式的收敛性及数
Zhi稳定性进行了分析;对于数值积分公式,还Gei出了精度的评价标准――代数精度,并由此Chu发,建立了精度最高的Gauss型求积公Shi.
?6.1
Jin管微积分是现代科学的重要基础与起点,并Qie已在物理、力学、化学、生物等自然科
Xue领域以及经济、管理等社会科学领域中有了Fei常广泛的应用,然而在微积分计算中,还至
Shao面临着如下问题.
(1) 被积函数的原函数不易求出或者根本Bu能用初等函数表出.例如,概率积分
22tx,ptedxt,,,,()(0) ,0,
和椭圆积分
t22 etkxdxt()1sin(02),,,,,,0
(2) 函数的表达式形式过于复杂,对其直Jie进行积分、求导运算,计算量很大;甚至对Yu
Yi些形式简单的函数进行积分,得到的原函数Ye可能非常复杂.例如
,,233dxx,,,arctgtg,C ,,,2cos332,x,,
Geng重要的是,尽管上式从形式上看是精确的,Ran而,用上式计算定积分时,因函数值不能做
Dao精确计算,最终得到的结果仍然是近似的,Bing且所引入的正切值和反正切值的计算量也不
小.
(3) 函数本身就是离散函数,如实验数据Deng,用经典的微积分知识无法求其导数值和积Fen
值.
Zai计算机发展迅速的今天,上述困难可以用数Zhi的方法予以解决.本章主要介绍常用的
Shu值微积分公式及其相关理论.
?6.2
Zai微分学中,函数的导数是通过导数定义或求Dao法则求得的.然而如果需要利用函数在
Xiang关离散节点处的函数值近似计算其导数,就Yao寻求其它的方法.一种方法是利用离散数据
Jin行插值,然后用插值函数的导数作为被插值Han数导数的近似;另一种方法是将不同点的函
Shu值在某一点Taylor展开,然后用其线Xing组合建立函数的导数值近似表达;另外,还Ke以根
92
Ju数值微分公式的截断误差,通过Richardson外推技巧建立更高精度的数值微分Gong式.
y,f(x) (i,0,1,2,?,n)Kao虑以表格形式给出的,定义于区间上的离散Han数:,[a,b]ii用第四章的插值方法Jian立该函数的插值多项式p(x).由于多项Shi的导数容易求得,可以取n
,,p(x)f(x)p(x),的导数作为Han数导数的近似,即取.由 f(x)nn
(1)n,f(), fxpxxab()()() (),,,,,, (6.1) nn,1(1)!n,
得到
(n,1),,(x)f()d(n,1)n,1 f(x)p(x),(x)f(,),,, (6.2) ,,,nn,1(n1)!(n1)!dx,,
d(n,1)上式中的x是与有关的未知函数,因此对于f(,)很难做出估计.但是,在Cha值节点,dx
处的导数值
(n,1),f() ,,,f(x),p(x),,(x)(0,i,n) (6.3) inin,1i(n,1)!进而得到函Shu在插值节点处的数值微分公式的截断误差
(n,1),f() ,,,,,,R(x)f(x)p(x),(x) (6.4) niinin,1i,(n1)!
(n,1)若函数在插值区间上有上界,即有 f(,)M
(n,1) f(,),M则得到数值微分公Shi的误差估计
M,,,R(x),f(x),p(x),,(x) niinin,1i(n,1)!可Yi看出,当插值节点之间的距离较为接近时,Tong过插值方法得到的数值微分公式有较高的
精度.
Chang用的数值微分公式是、时的插值型微分公式 n,1n,2
? 一阶两点公式()xx, 01
93
1(6.5),,f(x),f(x),(f(x),f(x))0110h
h,,Rxfxx()(),(,),,,,,1000012 (6.6) h111101,,Rxfxx()(),(,),,,,2
? 一阶三点公式()xxx,, 012
1,,,,,,,,,,f(x),,3fx,4fx,fx0012,2h,1, ,,,,,,, (6.7) f(x),fx,fx,1202h,
1,,,,,,,,,,f(x)fx4fx3fx,,,2012,2h,
1,2,,,Rxhfxx()(,),,,,,,200002,3,1, 2,,,,,Rxhfxx()(,) (6.8) ,,,,,,2111026,
1,2,,,,,Rxhfxx()(,),,,,222202,3,
Li用类似的思路,还可以建立高阶导数的数值Wei分公式.
Cong上面的数值微分公式的余项上来看,理论上Bu长取的越小,精度就越高.但在实际h计算Shi并不这样简单.
,kx6.1 设h,h,10 (k,1,2,?15)f(x),e,分别采用不同步Chang,使用公式(6.5)计0
Suan,f(1)的近似值.
显然,h,0.1f(1),e,2.71828182845905.取初始步长,分Bie记0,, f(1,h),f(1),,,YongMatlab软件编程计算,计算结果见表d,,/herror,d,e
6.1.
,7从表6.1可以看出,当步长从h,0.1,10到逐步减小时,得到的导数近似值的h,0.1
Wu差逐步减少;然而,随着步长的进一步减小,误差逐步增大.这是因为实际计算结果的误
Cha是由截断误差和舍入误差共同决定的,由截Duan误差表达式可知,不宜过大;但当小到 hh
94
6.1 例6.1计算结果
error dk ,
1 0.02731918655787 2.73191865578708 0.01363682732803 2 0.00271964142253 2.71964142253278 0.00135959407374 3 0.00027184177471 2.71841774707848 0.00013591861944 4 0.00002718295420 2.71829541991231 0.00001359145326 5 0.00000271828319 2.71828318698653 0.00000135852748 6 0.00000027182820 2.71828196396484 0.00000013550580 7 0.00000002718282 2.71828177744737 -0.00000005101167 8 0.00000000271828 2.71828159981169 -0.00000022864736 9 0.00000000027183 2.71827893527643 -0.00000289318262 10 0.00000000002718 2.71827005349223 -0.00001177496681 11 0.00000000000272 2.71827005349223 -0.00001177496681 12 0.00000000000027 2.71338507218388 -0.00489675627516 13 0.00000000000003 2.66453525910038 -0.05374656935867 14 0.00000000000000 2.66453525910038 -0.05374656935867 15 0 0 -2.71828182845905
Yi定程度时,公式的分子出现相近数相减,同Shi分母趋于零,舍入误差导致有效数字位数急
Ju减少,也同样导致求解精度的降低.
Taylor
She函数f(x)充分光滑,对于给定的步长,Li用 Taylor公式有 h
,,,,,f(x)f(x)23, ,,,,,,? (6.9) f(xh)f(x)f(x)hhh2!3!
,,,,,f(x)f(x)23, ,,,,,,? (6.10) f(xh)f(x)f(x)hhh2!3!
Cong而可建立数值微分公式
f(x,h),f(x)f(x,h),f(x) , (6.11) f(x),,O(h),hh
Qi截断误差为O(h)O(h).类似地,可Yi建立另一截断误差为数值微分公式
f(x),f(x,h)f(x),f(x,h) ,f(x),,O(h), (6.12) hh
2如将式(6.9)和式(6.10)相减,Ke建立截断误差为O(h)数值微分公式
95
,,,,,,f(xh)f(xh)f(xh)f(xh)2, (6.13) f(x),,O(h),2h2h
2类似地,将式(6.9)和式(6.10)Xiang加,可得截断误差为,,O(h)的计算的Shu值微分公式 f(x)
f(x,h),2f(x),f(x,h)f(x,h),2f(x),f(x,h)2,, (6.14) f(x),,O(h),22hh
Ruo利用更多点处的函数值(如)的Taylor展开式的线性组合,将可建(x,2h),(x,3h),?
Li具有更高阶的截断误差的数值微分公式.
Richardson
*S(h)假设利用某种数值方法得到某一量Yu步长有关的近似值,截断误差为 Sh
ppp*k12S,S()h,ah,ah,?ah,? (6.15) k12
Shi中0,p,p,?,p,?p,a(i,1,2,?)a,a,?,系数非零,且均是与Bu长无h12kii12
关的常数.
Yong代替上述公式中的步长,得 h/2h
ppp12khhhh,,,,,,,,* (6.16) SSaaa,,,,?,,?,,,,,,,,k122222,,,,,,,,
Ru将上述两式进行加权平均,有望消去误差级Shu中的第一项,得到精度更高的数值计算
Gong式.如在式(6.15)中,取
fxhfxh()(),,,*, SfxSh,,(),()2h并且根据
(5),,,fxhfxhfxfx()()()(),,,24,fxhh(),,,, (6.17) 23!5!h
可得
(5),,,fxhfxhfxfx()()()(),,,*24,SShfxhh,,,,,,,()() (6.18) 23!5!h
Ruo将式(6.18)中的用替代,有 h/2h
hh24fxfx()(),,,(5),,,hfxhfxh()(),,,,,,*22,SSfx,,,,,,,() (6.19) ,,,,,,23!25!2h,,,,,,
96
2将以上两式线性组合,并消去的系数得 h
hhfx,,fx,()()fx,h,fx,h41()()422, fx,,,Oh()()hh332
4h1**4 (6.20) ,S(),S(h),O(h)323
Zhe是Richardson外推算法的第一步.当然若有必要,还可以对式(6.20)继Xu进行外推运算
4(将式中的O(h)写成按幂次展开的形式). h
26.2 设,f(x),xcosx,试用Richardson外推法建立的数值公式(6.20)计算的f(1.0)
Jin似值(外推3次),初始步长取.计算结果Jing确到小数点后7位. h,0.1
计算结果见表6.2.
6.2 例6.2计算结果
(6.12)式计算结果 第一次外推 第二Ci外推 第三次外推 h
0.1 0.22673616
0.05 0.23603092 0.23912917
0.025 0.23835774 0.23913335 0.23913363
0.0125 0.23893964 0.23913361 0.23913363 0.23913363
?6.3 Newton -Cotes
bI(f),f(x)dx由高等数学的知Shi知,定积分定义为如下和式的极限 , a
n(x,x)f(,) ,i,1iii,0
Shi中axxxbxxin,,,,,,,,, [,](0,1,,1),,极限过程为Zui大的子区间长011niii,
Du趋于0.这个定义本身就给出了一种计算积Fen近似值的方法.数值积分实际上就是用一些
Dian处函数值的线性组合来近似计算定积分,即
nn bI(f),f(x)dx,Af(x),E[f],Af(x) (6.21) ,,iiii, ai,0i,0
nn式中称为求积系数,称为求积节点,它们Jun与被积函数f(x)无关,表示E[f],,,,Axiiii,0,0
97
Qiu积余项,也称为求积公式的截断误差.追求Li想的求积公式自然是希望其精确程度最高.
Gai括起来,数值积分需研究如下三个问题
(1) 求积公式的具体构造;
(2) 求积公式的精确程度衡量标准;
(3) 求积公式的误差估计;
Zhe里通过引入被积函数的插值函数以及求积公Shi代数精度的概念分析上述三个问题.
n设给定的个互异节点为,关于这些节点做被Ji函数的Lagrange 插n,1,,x,[a,b]ii,0
Zhi函数L(x),于是有 n
,,n,1,f() f(x)L(x),(x) (6.22) ,,nn,1(n1)!,Dui式(6.22)两端在积分区间[a,b]Shang积分,得
,,n1, b b b,f()fxdxLxdx,xdx,,nn1()()(),,,, a a a n,(1)!
,,n1n, b b,f() f(x) l(x)dx,(x)dx (6.23) ,,kkn1,,,, a a(n1)!k0,,
bn其中L(x)dxl(x)为关于节点DeLagrange插值基函数, 取作为积Fen的近似值,构,,xnkii,0, a造Chu插值型求积公式
n bf(x)dx,Af(x) (6.24) ,kk, ak,0其中求Ji系数
bA,l(x)dx (6.25) kk, a同时,求得该求积公式De求积余项为
,,n1, b,f()E[f],(x)dx (6.26) ,n1,, a(n1)!,Newton -Cotes
98
Jiang节点等距分布时建立的插值求积公式称为Newton -Cotes 求积公式.它的Si想最早出现于1676年Newton 写GeiLeibnitz(莱布尼茨) 的信中,Hou来Cotes(柯特斯) 对Newton 的方法进行了系统研究,于1711年给出Liao点数的所有公式的权.下面列出几个最简单、,10
Zui著名的Newton -Cotes 求积Gong式
(1) 用区间中点做零次插值多项式,得到Yi点Newton -Cotes 求积公式,称为中点求积公式,即
bab,,, ()():()fxdxbafMf,,, (6.27) ,,, a2,,
(2) 用区间两个端点做一次插值多项式,De到两点Newton -Cotes 求积Gong式,称为梯形求积公式,即
bba,()(()()):() (6.28) fxdxfafbTf,,,, a2
(3) 用区间两个端点及中点做二次插值多Xiang式,得到三点Newton -Cotes 求积公式,称为Simpson(辛普森)Qiu积公式,即
b,,baab,,,,,,fxdxfaffbSf,,,, (6.29) ()()4():(),,,,,,, a62,,,,,,
(4) 将区间四等分得到的五个节点(包括Qu间两个端点)做四次插值多项式,得到五点
Newton -Cotes 求积公式,称WeiCotes 求积公式,即
bfxdx(),, a
(6.30) baababab,,,,,,33,,,,,,7()3212327() :()faffffbCf,,,,,,,,,,,,,90424,,,,,,,,
Guan于更详细的Newton -Cotes Qiu积公式的求积系数,可以查表6.3得到.
116.3 试分别用一点、二点、三点、Si点以及五点Newton -Cotes公Shi计算积分dx, 01,x的近似值(计算Jie果取5位小数).
利用中点求积公式,得
,,
,, 111 dx,1,,0.66667,,, 011,x,,1,,,2,,
Li用梯形求积公式,得
1111,,dx,,1,,0.75000 ,,, 01,x22,,
Li用Simpson求积公式,得
99
6.3 Newton -Cotes 求Ji公式系数
,,nn A i
111
22
1412
666
13313
8888
732123274
9090909090
1975505075195
288288288288288288 412727412162722166
840840840840840840840 7513577132329892989357713237517
1728017280172801728017280172801728017280
,45409895888,9281049610496,92858889898
283502835028350283502835028350283502835028350
…… ……
,,
,, 11111 dx,,1,4,,,0.69444,,, 011,x62,,1,,,2,,
Li用四点Newton -Cotes求积公Shi,得
,,
,, 111111 dx,,1,3,,3,,,0.69375,,, 0121,x82,,1,1,,,33,,利用Cotes求积公式,得
,,
,, 1111117 dx,,7,32,,12,,32,,,0.69317,,, 01131,x902,,1,1,1,,,424,,事实上原积分的准确值为
11dx,,ln0.69315 2, 01,x
Ke见这五个公式的近似积分的精确程度不同,Qiu积节点越多,得到积分近似值越精确.
100
[9]由Weierstrass(维尔斯特La斯)多项式逼近定理可知,对任意给定的精Du要求,闭区
Jian上的连续函数都可以用多项式近似.一个很Zi然的做法就是用精确积分的被积多项式的次
Shu做为求积公式精确程度的度量.
6.1 若求积公式对于任意的不高于m次的Dai数多项式做为被积函数时都精确成立,
Er对某个m+1次多项式被积函数不精确成立,则称该求积公式具有m次代数精度.
You(6.26)式可知,n+1个求积节点的Cha值型求积公式的代数精度至少为n.
Rong易证明,求积公式具有m次代数精度的充要Tiao件是它对于2m都准确f(x),1,x,x,?x
m,1成立,而对于不准确成立. f(x),x
Tong过代数精度的定义容易验证,中点公式、Simpson公式、Cotes 公式的代数Jing度分别为1阶、3阶、5阶,但它们分别用Dao的是具有1个、3个以及5个求积节点的Newton -Cotes公式.从中可以看Dao这样一个规律:当插值节点的个数(n,1)是奇数时的Newton -Cotes求Ji公
[6]式的代数精度至少为阶,其证明见参考Wen献. n,1
Li用代数精度的定义也可以确定数值积分公式Zhong的相关参数,目标是使求积公式的代数
2精度尽可能高.只需要依次取被积函数1,x,x,?为,并通过使求积公式准确成立来Jianf(x)
Li适当数目的方程,进而求解未知参数.
6.4 试确定参数A,B,C,使得求积公Shi
2f(x)dx,Af(0),Bf(1),Cf(2) , 0
De代数精度尽可能高.
2 根据代数精度的定义,令f(x),1,x,x时,求积公式精确成立,得
A,B,C,2,, B,2C,2,
,B,4C,8/3,
解之得
141A,,B,,C, 333
3取,,fx,x,则
101
23xdx,4 , 0
413,,,, Af0,Bf1,Cf(2),,,2,433此时,该求积公式至少具You3次代数精度.
4取,,fx,x,有
2324 xdx,, 05但是
41204,,,, Af,Bf,Cf,,,,01(2)2333
42因此,当时,求积公式达到最高的代数精Du,且代数精度的次数为3次. A,0,B,,C,33
Li6.4实际上是积分区间取时的Simpson求积公式.可以看到,在固定求积节点的[0,2]
Qing况下,用待定系数法得到的求积系数和用插Zhi法建立的求积公式的求积系数是相同的.这
Shi因为,用待定系数法建立的形如式(6.21)的求积公式至少具有n次代数精度,而至Shao具有n
[6]次代数精度的求积公式一定是插值型的.
Newton -Cotes
6.1 设函数f(x)在积分区间[a,b]上具有连续的二阶导数,则中点求积公式De截断误差为
3()ba,,,,,Effab[]() (),,, (6.31) M48
由Taylor展开公式
2,,abababfab,,,,(),,,,,,,,,, fxffxxab()(),,,,,,,,,,,,,,,,2222!2,,,,,,,,
Dui上式两端在区间[a,b]上积分,有
2 b b,,,a,bfa,b(),,,, fxdxxbafxdx,,,,()(),,,,,, a a22!2,,,,
2a,b,,由于函数,,[a,b][a,b]在积分区间内不变号,而函数f(,)在Shang连g(x),x,,,2,,
102
Xu,由积分第二中值定理知,在内存在一点,Shi得 (,)ab,
23b ,,f,()a,b(b,a),,,, E[f],x,dx,f(,),,M, a2!248,,
6.2 设函数在积分区间上具有连续的二Jie导数,则梯形求积公式的截断f(x)[a,b]
误差为
3()ba,,,,,Effab[]()(),,,, (6.32) T12
梯形求积公式的余项为
b,,f(), Efxaxbdxab[]()() (),,,,,,T, a2!
You于,,,(x),(x,a)(x,a)在Ji分区间[a,b]内不变号,而函数在[a,b]上连续,f(,)2
You积分第二中值定理知,在内存在一点,使得 (,)ab,
3b ,,f(,)(ba),,,E[f],(x,a)(x,b)dx,,f(,) T, a2!12
6.3 设函数f(x)在区间[a,b]Shang有连续的四阶导数,则Simpson公式De截断误差为
5()ba,(4),,Effab[]()(),,,, (6.33) S2880
对区间H(x)[a,b]上的函数f(x),构造次数不高于3次的插值多项式,使得 3
H(a),f(a), H(b),f(b) 33
a,ba,ba,ba,b,,,,,,,,,,, H,fH,f ,,,,,,,,332222,,,,,,,,不难得到
24,,f(,)a,b,, f(x),H(x),(x,a)x,(x,b) a,,,b,,34!2,,
Dui上式两端在区间[a,b]上积分
103
2,,4 b b b,f()a,b,, f(x)dx,H(x)dx,(x,a)x,(x,b)dx,,3,,, a a a4!2,,因Simpson公式的代数精确Du是3,所以
b,,,,b,aa,b,,f(x)dx,,H(a),4H,H(b),,,,,333,,, a62,,,,,,
2,,4 b,f()a,b,, ,(x,a)x,(x,b)dx,,, a4!2,,
,,,,b,aa,b,, ,,f(a),4f,f(b),,E[f],,,,S,,62,,,,,,式中
2,,4b ,f,()ab,,,,,,E[f](xa)x(xb)dx,,S,a 4!2,, 2,,45b ,,f(,)ab(ba),,,,4,,,,,,(xa)x(xb)dxf(,),,,a 4!22880,,
Ding理6.3所使用的证明方法也可以用来证明Ding理6.1.对于更为复杂的Cotes 公Shi,有
6.4 设函数f(x)在区间[a,b]Shang有连续的6阶导数,则Cotes 公式的Jie断误差为
62()baba,,,,6,, (6.34) Effab[]() (),,,,,,4,,9454,,
Newton -Cotes
Ben节简要分析Newton –Cotes公Shi序列的收敛性及稳定性.
6.2 Newton -Cotes求积Gong式的是指,对于任意连续的被积函数,当求Ji节
Dian的个数n,,时,截断误差序列满足. limE[f],0nn,,
Newton -Cotes 求积公式是基Yu等距插值建立起来的,但因当n,,时,插Zhi函数不保证收敛到被插值函数,进而也不能Bao证. limE[f],0nn,,
Newton -Cotes求积公式序列的Wen定性主要考虑函数值f(x)计算的舍入误Cha对数值积分i结果的影响.
,,6.3 对于一个求积公式序列f(x)e,假设在计算时,引入舍入误差,If(),,iinn0,
~即有,并记 f(x),f(x),eiii
104
nn~~I(f),Af(x),I(f),Af(x) ,,niiniii,0i,0
Ru果对任意给定的小正数,只要误差,,maxe充分小,就有 ,,0ii
n~~ I(f),I(f),A[f(x),f(x)],,,nniiii,0
,,则称该求积公式序列是的. If(),,nn0,
对于数值求积公式,有
nnnn~ A[f(x),f(x)],Ae,Ae,A,,,,,iiiiiiiiiiii,0,0,0,0
You于Newton -Cotes求积公式对Chang数均能精确积分,当被积函数时,有 f(x),1
n在n,,A的过程中,Newton -Cotes求积公式序列的求积系数有正有负,De有界性不,ii,0
Neng保证,因而Newton -Cotes求Ji公式得稳定性不能保证.
Ji于上述稳定性、收敛性原因,在实际计算中,人们并不追求高阶的Newton -Cotes 求
Ji公式,而是通过细化积分区间的方法,用复Hua求积公式来提高数值积分的精度.
?6.4
Cong积分的定义可以看出,增加求积节点数目可Yi提高数值积分的代数精度.但通过增加
Cha值节点建立的高阶Newton -Cotes求积公式的稳定性差.一种提高求积精度De方法是先将整
Ge积分区间细分,然后在每个小的区间上使用Di阶的Newton -Cotes 求积公Shi,这就是复化求积法.理论和数值结果都表Ming,这种方案可以获得理想的数值结果.
b,an首先将积分区间[a,b] 等分,Qu间长度,节点记为h,n
xaihin,,, (0,1,,)[x,x],然后在每个小区间上使用梯形公式,De ii,1i
105
n,1 b xi,1f(x)dx,f(x)dx,,, a xii,0
3n,1hh,, ,[(f(x),f(x)),f,()],ii,1i212i,0
3n,1n,1hh,,,,,f(a),2f(x),f(b),f(,),,,,ii212i,1i,0,,略去上式最后一项,De到复化梯形公式
n,1h,, (6.35) Tf(a)2f(x)f(b),,,,,,ni2i,1,,其截断误Cha为
31n,h,,Efxx,,,,() (),, 1Tiiii,,n0i,12
6.5 设函数f(x)在积分区间[a,b]上具有连续的二阶导数,则复化梯形公式的Jie断
误差为
ba,2,,() (),, (6.36) Ehfab,,,,Tn12
因为,,mf(x)在[a,b]Shang连续,则其在区间一定有最大值和最小值,Ji M
,,mfMxxab,,,,(),(,)[,],, iiii,1进而有
n,11,,m,f(,),M i,i,0n
You连续函数的介值定理知,存在一点,,,,a,b,使得
n,11,,,,,f,()f(,) i,i,0n
故
n,31,hba2,,,,,,,,Ef,()hf(,) Ti,ni,12120
Cong截断误差可以看出,复化梯形公式的代数精Du仍为一阶. 106
Simpson
Ruo在每个小区间上使用Simpson公式,You
i,1n,1f(x)dx,f(x)dx b x,i,, a xi,0,,,,hh5n,1n,1,,,,,,4,f(x),4fx,f(x),f,() ,,,,,,i1i,1i62880i,,,i,0i,0,,2
5n,1n,1n,1,,,,hh4,,,,,,,f(a),2f(x),4fx,f(b),f(,)i1i,,,i,,,,,i,1i,0i,0628802,,,,上Shi略去最后一项,得到复化Simpson公Shi
n,1n,1,,,,h,,,,Sf(a)2f(x)4fxf(b) (6.37) ,,,,ni1,,i,,,,,i,1i,062,,,,其截断误差Wei
51n,h4,,Efxx,,,,() (),, 1Siiii,,n0i,2880
6.6 设函数,,,,fxa,b在区间Shang有连续的四阶导数,则复化SimpsonGong式的截断误差为
ba,4,,4() (),, (6.38) Ehfab,,,,Sin2880
Cong截断误差可以看出,复化Simpson公Shi的代数精度仍为三阶.
Dui于上节的中点求积公式,使用同样的方法,Ye可以获得其对应的复化求积公式以及截
断误差
n,1,,Mhfx,n1,,,i,i,02,, 2ba,M,,Rhfab,,,() (),,n48
[6]可以证明这三个复化求积公式都是收敛De、稳定的.
, /26.5 使用复化梯形公式和复化Simpson公式计算定积分cosxdx的Jin似值时,要, 0
,5求误差不超过10,分别需要多少个求积Jie点?
107
,,ba,,, 这里,. , , max1bahf,,,,,,,,ab,,,22nn
,5从复化梯形公式的截断误差可知,要使得Jin似值的误差不超过10,则需满足
b,a2,5,,,,max,hf,,10 a,b,,12解不等式得
n,179.7170取,相应的需要个求Ji节点; n,180n,1,181
Tong理,用复化Simpson公式计算时,需Man足
b,a4(4),5,,max,hf,,10 a,b,,2880
4,b,a,,,5(4)由于,,10,,maxf,,1,解得,,因此,需要将区间Jin行n,4.2688,,a,,,b28802n,,
Deng分,相应的需要个求积节点. n,52n,1,11
Shi用复化求积公式计算积分值,要保证满足指Ding精度,依据截断误差,需要将中值定理
Shi用时产生的被积函数的高阶导数在某一点的Jue对值放大为整个积分区间上的最大值,若,Zui大值难求,还需进一步进行放大运算,势必Dao致过多地选取求积节点,影响计算效率.
Qu间逐次分半求积法则避免了这种不便.它是Gen据规定的精度要求,在计算过程中把积
Fen区间逐次分半,利用相邻两次求积结果之差Lai判别误差的大小,从而得到满足精度要求的
Ji分近似值.下面以复化梯形公式为例来说明Qu间逐次分半求积法的计算过程.
2由复化梯形公式的误差估计式可以看到,n.当对较大时,可以认为 E,O(h)Tn
2 (6.39) E,chTn这里c为常数,当将区间等分时You 2n
2h,, (6.40) E,c,,T2n2,,进而
,ITn,4 (6.41) ,IT2n即
108
1 (6.42) I,T,(T,T)2n2nn3
1上式说明,若用T作为准确值I的近似值时,误差大约为.因此可以使用(T,T)2n2nn31,T(T,T),,判断近似值的Jin似程度,其中为容许误差,这样就避免了被Ji函数高2n2nn3
Jie导数最值的估计.
Xu要指出的是,在实际计算T时,由于每次总Shi在前一次对分的基础上将区间再次对分,2n
Fen点加密一倍,原分点上的函数值不需要重复Ji算,这样可以采用如下的递推公式减少计算
量
nT,,,1hba,,n (6.43) ,,,,,,,,Tfaihh,,,n2,,222n,,i,1,,
Tong理,也可以类似的给出基于复化Simpson公式和复化Cotes 公式的区间逐次Fen半求积
法,此时有
1I,S,(S,S) (6.44) 2n2nn15
1I,C,(C,C) (6.45) 2n2nn63
6.1
Shu入 区间端点,及精度; a,b
Shu出 积分近似值; T
Step 1 令T,h(f(a),f(b)),h,(b,a)/2,,; n,1hh,/20
Step 2 令,对i,1,2,?,n,Ji算F,F,f(a,(2i,1)h); //计算新节点函数值和 F,0
Step 3 计算T,T/2,hF; //计算式(6.43) 0
Step 4 若n,2n,h,h/2,T,T,算法终止,输出;否则,赋值,转Step2. T,T,,T00
6.2 simpson
Shu入 区间端点,a,b及精度;
Shu出 积分近似值; S
109
,,h,b,a/4Step 1 令,; n,2
Step 2 计算,,FfafbFfab,,,,()(),(()/2),S,b,a(F,4F)/6,; hh,/200101
Step 3 令,,F,0F,F,fa,(2i,1)h,对,计算;//计算新节点Han数值和 i,1,2,?,n222Step 4 计算S,h(F,2F,4F)/3; 012
Step 5 若n,2n,h,h/2,S,S,算法终止,输出;否则,令, SS,S,,00
F,F,F转Step3. 223
1sinx6.6 使用复化梯形公式和复HuaSimpson公式计算定积分的近似值,Yao求误dx, 0x
,5差不超过,,10.
使用区间逐次分半求积法的复化梯形公式和Fu化Simpson公式进行求解.计算结果Ru
k表6.4所示,其中等分区间间距为:h,(b,a)/2,算例使用 和T,T,,S,S,,2nn2nn
Zuo为误差终止判断条件.
6.4 例6.6的计算结果
Fu化梯形公式近似值 复化Simpson公Shi近似值 k
0 0.9207355
1 0.9397933 0.9460869
2 0.9445135 0.9460833
3 0.9456909
4 0.9459850
5 0.9460586
6 0.9460769
7 0.9460815
?6.5 Romberg 一、Romberg求积法
11TS区间逐次分半求积法将(T,T)或(S,S)处理成误差,将或作为积分2n2n2nn2nn315
110
T(S)T(S)的近似值.分析近似表达式(6.45)和(6.47)后可以发现,既Ran和都已经算出,nn2n2n
111自然地,误差或也可以算出,那么将或(T,T)(S,S)T,(T,T)2nn2nn2n2nn3153
1整体作为积分的近似值,显然可进一步改善Ji分计算精度. S,(S,S)2n2nn15
事实上,可以验证
1 (6.46) T,(T,T),S2n2nnn3
Shang式表明对基于区间逐次分半求积的复化梯形Gong式进行误差校正得到复化Simpson求Ji公式
24的计算值,从而把误差从O(h)O(h)提高到.
类似地,有
1 S,(S,S),C(6.47) 2n2nnn15 即对基于区间逐次分Ban求积的复化Simpson公式进行误差校Zheng得到复化Cotes求积公式的计
46算值,误差从O(h)O(h)提高到.
Wo们称基于区间逐次分半求积的复化Cotes公式进行误差校正得到的公式为Romberg(龙贝格)求积公式
1 (6.48) C,(C,C),R2n2nnn63
8它的误差阶是O(h).
Er、Richardson
Romberg求积算法还可以通GuoRichardson外推技巧得到.文献[4]给出了复化梯形公式的渐近展开形式的Wu差表达
b246fxdxTahahah(),,,,, (6.49) n246, a
Qi中,a,a,a?是与步长无关的常数. h246
,,使用基于复化梯形公式的区间逐次分半求Ji法,可得T. ,,nn,1
Xian将Richardson外推技巧用到式(6.49),经过一次外推得到
111
b41(1)4(1)6 (6.50) fxdxTTahah,,,,,()246nn, a33
41而由式(6.46)知,于是有 STT,,nnn233
b(1)4(1)6 fxdxSahah(),,,, (6.51) n46,a
Zhe与定理6.6一致.
Lei似地使用Richardson外推技巧,Huan可以依次得到式(6.47)和式(6.48) .
6.3Romberg
Shu入 积分区间端点参数,及精度; a,b
Shu出 积分近似值;
Step 1计算初值; Tbafafb,,,()()/2,,,,1
ba,iStep2 令(1,2,;2),An式 (6.43) 计算梯形序列; hin,,,T,,nn
Step 3 分别按式 (6.46) 、Shi (6.47)、 式 (6.48) 计Suan序列、; SCR,,,,,,nnnStep 4若,算法终止,输出;否则,区间分Ban,转Step2. Rn(2)RnRn(2)(),,,
14,76.7 使用Romberg求积Fa计算定积分,,10的近似值,要求误差不Chao过. dx2, 01,x
n 计算结果如表6.5所示,其中等分区间Jian距为:h,(b,a)/2,算例使用
Zuo为误差终止判断条件. R,C,,nn
6.5 例6.7的计算结果
n 梯形序列(I (n,0)) Simpson序列(I (n,1)) Cotes 序列(I (n,2)) RombergXu列(I (n,3))
0 3
1 3.10000000 3.13333333
2 3.13117647 3.14156863 3.14211765
3 3.13898849 3.14159250 3.14159409 3.14158578
4 3.14094161 3.14159265 3.14159266 3.14159264 容易计算
14dx,,,3.1415926535897?? 2, 01,x
Ke以看到,当时,使用基于复化梯形公式的区Jian分半求积法,误差是 k,4
112
,,3.1409416,0.0006510??但是通过外推之后,得到的龙贝格序列De误差减小为
,,3.14159264,0.00000001??计算精度得到了很大提高.
?6.6 Gauss 前面研究的数值求积Gong式都是在积分区间内事先确定了个求积节点,然后通过待定n,1系数法,按照使求积公Shi的代数精度达到最高的原则选取最佳求积系Shu(和通过插值的方法
De到的求积系数是一致的).已经知道,对于Ju有个求积节点的求积公式,其代数精度n,1
Zhi少可以达到n次.那么能否适当地选择求积Jie点的位置和相应的求积系数,使得求积公式
Ju有更高甚至最高的代数精度?答案是肯定的.例如下面的求积公式
,,,, 133 ,,,,,,fxdx,f,,f ,,,,,, 133,,,,可以验证,该公式的代数精确度是3次,而前述的两点Newton -CotesGong式即梯形求积公式的代数精度只能达到1次.
n实际上,对任意一组{x}个互异求积节点De插值型求积公式,当被积函数n,1ii,0
f(x)取为次的多项式 2n,2
2222 ,,,,,,,()x,x,xx,x?x,x101,nn时,总有
nb 22I(f),,(x)dx,A,(x),E[f],E[f],0 (6.52) ,n,in,i11,a i,0
Ji对任意的个互异求积节点构造的求积公式的Dai数精度不能达到次,那么是否能n,12n,2够达到次,则是本节考虑的问题. 2n,1
Gauss
Yi般地,如果选取个求积节点,要使求积公式Dui任意的次多项式精确成立,n,12n,1Gen据待定系数法,有
113
b,,,,,,AAAdxba101n, a,
22, bba,,AxAxAxxdx,,,,0011nn,, a2 (6.53) ,
,
,,,2222nn bba,,,,,21212121nnnn,,,,,AxAxAxxdx0011nn, a,22n,,
Li论上可以证明,上述非线性方程组的解是存Zai惟一的.也就是说,通过合理地选取求积节
Dian及求积系数,可以使得求积公式的代数精度Da到次.将这种具有个求积节点的2n,1n,1
Ju有次代数精度的求积公式称为Gauss,Dui应的一组求积节点称为一组2n,1
Gauss.
Gauss型求积公式的求积节点和求积系数Ke以通过求解非线性方程组(6.53)得到,然而,直接求解该非线性方程组是复杂的.Tong常构造Gauss型求积公式的方法是,首Xian通过正交多
Xiang式确定一组Gauss点,然后再使用待定Xi数法或插值的方法求出Gauss型求积公Shi的求积系数.
6.7 对于插值型求积公式,其互异节点n{x}是一组Gauss点的充分必要条件Shi以ii,0
Zhe些点为零点的多项式函数,()()()()xxxxxxx,,,,与任意的次数不超Guon次的nn,101
Duo项式函数,,a,b在积分区间上正交,即Man足 p(x)
b (6.54) ,(x)p(x)dx,0n,1,a
(充分性) 对任意不超过2n+1次的Duo项式,存在不超过n次的多项式和g(x)q(x)
,使得 r(x)
g(x),q(x),(x),r(x) (6.55) n,1
Cheng立.对上式两端积分,得
bbbb (6.56) g(x)dx,q(x,)(x)dx,r(x)dx,r(x)dxn,1,,,,aaaa
n对互异节点组{x},构造插值型求积公式,即取求积系数 ii,0
114
nx,xbjA,dx(k,0,1,?,n) (6.57) ,k,ax,x,0jkj ,jk
Zhe样求积公式至少具有n次代数精度.
利用代数精度概念有
nnbr(x)dx,Ar(x),Ag(x) (6.58) ,,iiii,a ,0,0ii
Bi较式(6.56)和式(6.58),有
nb g(x)dx,Ag(x) (6.59) ii,a,i,0
Zhe样求积公式具有2n+1次代数精度,积分Jie点是一组Gauss点.
nn(必要性) 节点{x}{A}是一组Gauss点,是相应的Gauss求积系数,Zhe样的求积公iiii,0,0
Shi具有2n+1次代数精度.设p(x),(x)是任意不超过n次的多项式,不超过2n+1次. p(x)n,1
nb p(x),(x)dx,Ap(x),(x),0 (6.60) ,n,1iin,1i,ai,0
Zhe说明式(6.54)成立.
You定理6.7可知,只要能够找到与任意的次Shu不超过n次的多项式函数在区间[a,b]p(x)
Shang正交的n+1次多项式函数,那么,这个函Shu的所有零点即为Gauss点.下面以Legendre (勒让德) 多项式为例,介ShaoGauss型求积公式的构造过程.
Gauss-Legendre
称形如
n 1 f(x)dx,Af(x) (6.61) ii,, ,1i,0
DeGauss型求积公式为Gauss-Legendre. 可以证明,该求积公式对应Den+1个Gauss点正好是n+1次勒让De多项式
n,11d2n,1 (6.62) p(x),(x,1)n,1n,1n,1(n,1)!2dx
115
De一组零点.在求得一组Gauss求积节点Hou,求积系数可通过待定系数法或插值型求积Gong式
De求积系数公式求得.表6.6给出了部分Gauss-Legendre求积公式的求积Jie点和求积系数.
6.6 Gauss-Legendre求Ji公式中的数据
Ax n kk
0 0 2
1 ?0.5773502692 1
?0.7745966692 0.5555555556 2 0 0.8888888889
?0.8611363116 0.3478548451 3 ?0.3399810436 0.6521451549
?0.9061798459 0.2369268851
4 ?0.5384693101 0.4786286705
0 0.5688888889 和上一节描Shu的求积公式不同的是,Gauss-Legendre求积公式的积分区间是[,1,1],对于
b定积分f(x)dx,可以通过变量代换 , a
a,bb,ax,,t (6.63) 22
Jiang区间[a,b]上的积分转化为[,1,1]上的积分
b 1baabba,,,,,f(x)dxftdt,, (6.64) ,,,,, a 1222,,然Hou再使用Gauss-Legendre求积Gong式进行计算.
6.8 分别使用两点Gauss-Legendre求积公式和四点Gauss-Legendre求积公式计算定
, /2积分cosxdx的近似值. , 0
, 作变量代换x,(1,t),则 4
, /2 1,,,,Icosxdxcos(1t)dt,,, ,,,, 0 1,44,,116
,,,t,0.5773503A,A,1t,,0.5773503记,,因为节点,,,由(t),cos(1,t),,00114,,
Liang点Gauss-Legendre求积公式De
, I,(,(t),,(t)),0.9984726016014
Tong样地,取t,0.8611363116t,,0.8611363116t,0.3399810436,,,012t,,0.3399810436A,A,0.347854845A,A,0.6521451549,,,由四点30123Gauss-Legendre求积公式得
,I,(A,(t),A,(t),A,(t),A,(t)),0.9999999772 001122334
,/2易知,I,cosxdx,1.四点Gauss-Legendre求积公式的误Cha为 , 0
,7 1,0.9999999772,10
,5而由例6.3可知,要求误差不超过10,复化梯形公式和复化Simpson公式分Bie需要181个
Qiu积节点和11个求积节点.可见,Gauss型求积公式具有较高的计算精度.但是,当Qiu积节
Dian数目增加时,Gauss点发生了变化,前Mian计算的函数值不能在后面使用.
Gauss
6.8 设被积函数的2n+2阶导函数在区Jian上连续,则Gauss求积公式的f(x)[a,b]截断误差为
n(22),b,f()2 R[f],,((x))dx,,(a,b) (6.65) n1,,a(2n,2)!
设H(x)是满足如下插值条件的不超过2n+1次的插值多项式 2n,1
H(x),f(x),2n,1kk (6.66) (k,0,1,?,n),,,H(x),f(x)2n,1kk,
Ze其插值余项可表示为
117
(22)n,f,()2 (6.67) f(x),H(x),(,(x)),,(a,b)211n,n,(2n,2)!
You于Gauss型求积公式具有次代数精度,Yin此 2n,1
nnb H(x)dx,AH(x),Af(x) (6.68) ,,2,12,1niniii,a,0,0ii
Gu,求积公式截断误差可以表示为
nb R[f],f(x)dx,Af(x) ,ii,a,0i
bb ,f(x)dx,H(x)dxn2,1,,aa
n(22),bf,()2 (6.69) (,(x))dx,n1,,a(2n2)!,
2因为(,(x))在求积区间上不变号,的2n+2阶导函数在求积区间上连续,对式f(x)1n,
(6.69)使用积分第二中值定理便得到式(6.65) .
Dui于Gauss型求积公式,其求积系数
nb22AAlxlxdx,,,(())(())0(6.70) kikk,,ai0,
nn其中,{l(x)}{x}是以Gauss点为插值节点的Lagrange插值基函Shu.上式表明Gaussiiii,0,0
Qiu积系数都大于零,进而得到如下定理
6.9 Gauss型求积公式序列是稳定De、收敛的.
118
Cha值法建立数值微分公式
Taylor法建立数值微分公式 数值微Fen
Richardson外推法建立高阶数值微Fen公式
数
Cha值法建立求积公式 值
Wei 基本概念 代数精度 分 收敛性与稳定Xing 与
Shu 具体公式 值 代数精度 Newton-Cotes公式 积
截断误差 分
复化梯形公式
数值积分
Fu化求积公式 复化Simpson公式
Qu间逐次分半求积算法
Romberg求积公式
基本理论
Gauss-Legendre公式 Gauss型求积公式
Jie断误差 Gauss-Legendre公Shi
[x,2h,x,2h]x,x,kh1 Shef(x)在区间上有连续的四阶导数, (2,1,0)k,,,,00k0
试证明
141) ,f(x),,,f(x),8f(x),8f(x),f(x),O(h); 0,2,11212h
119
12,,2) f(x),,,f(x),f(x),2f(x),O(h)0,1102h
2 已知函数的下列数据 f(x)
k 1.8 2.0 2.2 2.4 2.6
k f(x) 3.12014 4.42659 6.04241 8.03014 10.46675 x 分别用一阶中点公式和Er阶中点公式计算,,,和的近似值. f(2.2)f(2.2)3 Archimedes(阿基米德)通过计算半径为1的圆De内切和外切正多边形的周长得到,的近
Si值.n边内切多边形的周长为
,,p,nsin,/n, n
n边外切多边形的周长为
,,q,ntg,/n, n
Zhe两个值分别给出了,值的上下限.
1) 利用Taylor公式,证明pq和可Xie成如下形式 nn
24p,a,ah,ah,?,012n 24q,b,bh,bh,?,012n
Qi中,a,b.求出精确的. h,1/n00
2) 设,p,3.0000,p,3.1058,用Richardson外推法做一次Wai推,得到值的更好近612
Si.类似地,设,q,3.4641,q,3.2154,用Richardson外推法Zuo一次外推,得到值612
的更好近似.
4 试建立如下一点数值求积公式
2b(b,a) 1)左矩形公式 ,,,,f(x)dx(ba)f(a)f(,) 1,a2
2b(b,a) 2)右矩形公式 ,,,,f(x)dx(ba)f(b)f(,) 2,a2
式中,,,,(a,b). 12
5 确定下列求积公式中的参数,使得其代Shu精度尽量高,并指明其代数精度.
120
h1) f(x)dx,Af(,h),Af(0),Af(h),101,h,
112) f(x)dx,[2f(x),3f(x),f(1)]12,,13
6 证明:Romberg阵列中第二列是Dui被积函数应用Simpson公式的结果,Ji验证式(6.46).
27 要使积分的近似值具有6位有效数字,若用复化Simpson或复化梯形求积公Shilnxdx,1
Fen别需使用多少个节点处的函数值?
1,x8 用Romberg求积算法计算De近似值,使它具有5位有效数字. edx,0
9 利用Gauss求积公式和Newton-Cotes求积公式(都取四个求积节点)计算积分
11dx,201,x
De近似值,并比较结果.
1410 (数值实验) 已知积分,试比较Ru下三种方法计算该积分近似值时,若xlnxdx,,,09
,7要使结果的误差不超过10,各调用了被Ji函数多少次?
Suan法1 基于区间逐次分半法的复化梯形公Shi;
算法2 基于区间逐次分半法的复HuaSimpson公式;
算法3 Romberg求积公式.
11 (数值实验) 用给定的方法求值
11)用Romberg求积公式计算积分,k,x1k,0,1,?,20,; I,exedxk,0
2)证明上述积分满足递推公式
I,1,kI kk,1
,1从I,1,eI出发,用递推关系计算,k,1,?,20的近似值; 0k
3)取I,0,从出发,利用向后递推公式 k,20k
I,(1,I)/k k,1k
QiuI的近似值.用不同的做试验,观察对结果Jing度的影响. kk
12 (数值实验) 用数值微分公式(6.15)计算中点导数的近似值,试以求对数函Shu在0.01,lnx
20.1,1,10处导数近似值为例,分析Ji算精度随步长h的变化规律,误差是否和O(h)同
121
Jie,是否步长越小计算精度越高?
122
数值分析原理第六章
Di六章 数值微分与数值积分
Ben利用函数的插值理论,构造了相应的数值微Fen与数值积分计算公式,并通过Richardson(理查森)外推技巧提高了这些公式De计算精度;另外,本章还对所建立公式的收Lian性及数值稳定性进行了分析;对于数值积分Gong式,还给出了精度的评价标准――代数精度,并由此出发,建立了精度最高的GaussXing求积公式(
?6.1 引 言
Jin管微积分是现代科学的重要基础与起点,并Qie已在物理、力学、化学、生物等自然科学领Yu以及经济、管理等社会科学领域中有了非常Guang泛的应用,然而在微积分计算中,还至少面Lin着如下问题(
(1) 被积函数的原函数不易求出或者根本Bu能用初等函数表出(例如,概率积分
22t,xptedxt,,,,()(0) ,0,
和椭圆积分
t22 etkxdxt()1sin(02),,,,,,0
(2) 函数的表达式形式过于复杂,对其直Jie进行积分、求导运算,计算量很大;甚至对Yu
Xing式简单的函数进行积分,得到的原函数也可Neng非常复杂(例如 一些
,,233dxx,,,arctgtg,C ,,,2cos332,x,,
Geng重要的是,尽管上式从形式上看是精确的,Ran而,用上式计算定积分时,因函数值不能做Dao精确计算,最终得到的结果仍然是近似的,Bing且所引入的正切值和反正切值的计算量也不Xiao(
(3) 函数本身就是离散函数,如实验数据Deng,用经典的微积分知识无法求其导数值和积Fen值(
Zai计算机发展迅速的今天,上述困难可以用数Zhi的方法予以解决(本章主要介绍常用的数值Wei积分公式及其相关理论(
?6.2 数值微分公式
Zai微分学中,函数的导数是通过导数定义或求Dao法则求得的(然而如果需要利用函数在相关Li散节点处的函数值近似计算其导数,就要寻Qiu其它的方法(一种方法是利用离散数据进行Cha值,然后用插值函数的导数作为被插值函数Dao数的近似;另一种方法是将不同点的函数值Zai某一点Taylor展开,然后用其线性组He建立函数的导数值近似表达;另外,还可以Gen
92
Ju数值微分公式的截断误差,通过Richardson外推技巧建立更高精度的数值微分Gong式(
一、插值法
y,f(x) (i,0,1,2,?,n)Kao虑以表格形式给出的,定义于区间上的离散Han数:,[a,b]ii
p(x)用第四章的插值方法建立该函数的插Zhi多项式(由于多项式的导数容易求得,可以Qun
,,p(x)f(x),p(x)的导数作为Han数导数的近似,即取(由 f(x)nn
(1)n,f(),,,,,fxpxxab()()() () (6.1) ,,nn,1,(1)!n
得到
(n,1),(x),f()d(n,1)n,1,,,f(x),p(x),,(x),f(,) (6.2) nn,1,,(n1)!(n1)!dx
d(n,1)x上式中的,是与有关的未知函Shu,因此对于很难做出估计(但是,在插值节Dianf(,)dx
处的导数值
(n,1),f(),,,f(x),p(x),,(x)(0,i,n) (6.3) inin,1i(n,1)!
Jin而得到函数在插值节点处的数值微分公式的Jie断误差
(n,1),f(),,,R(x),f(x),p(x),,(x) (6.4) niinin,1i(n,1)!
(n,1)f(,)若函数在插值区间上有上Jie,即有 M
(n,1)f(,),M
De到数值微分公式的误差估计 则
M,,,R(x),f(x),p(x),,(x) niinin,1i(n,1)!可Yi看出,当插值节点之间的距离较为接近时,Tong过插值方法得到的数值微分公式有较高的
精度(
Chang用的数值微分公式是、时的插值型微分公式 n,1n,2
()xx,? 一阶两点公式 01
93
1(6.5),,f(x),f(x),(f(x),f(x))0110h
h,,Rxfxx()(),(,),,,,,1000012 (6.6) h,,Rxfxx()(),(,),,,,1111012
()xxx,,? 一阶三点公式 012
1,,f(x),,,,3f,,,,,,x,4fx,fx0012,2h,1,, ,,,,,, (6.7) f(x),fx,fx,1202h,
1,,,,,,,,,,f(x)fx4fx3fx,,,2012,2h,
1,2,,,,,Rxhfxx()(,),,,,200002,3,1,2,,, (6.8) Rxhfxx()(,),,,,,,,,2111026,
1,2,,,Rxhfxx()(,),,,,,,222202,3,
Li用类似的思路,还可以建立高阶导数的数值Wei分公式(
Qu的越小,精度就越高(但在实际从上面的数Zhi微分公式的余项上来看,理论上步长h
Ji算时并不这样简单(
,kxh,h,10 (k,1,2,?15)f(x),e例6.1 设,分别采用不同Bu长,使用公式(6.5)计0
,f(1)算的近似值(
,h,0.1f(1),e,2.71828182845905解 显然(取初始步长,Fen别记0,, f(1,h),f(1),,,用Matlab软件编程计算,计算结果见Biaod,,/herror,d,e
6.1(
,7h,0.1,10从表6.1可以看出,Dang步长从到逐步减小时,得到的导数近似值的h,0.1
Wu差逐步减少;然而,随着步长的进一步减小,误差逐步增大(这是因为实际计算结果的误Cha是由截断误差和舍入误差共同决定的,由截Duan误差表达式可知,不宜过大;但当小到 hh
94
Biao6.1 例6.1计算结果
error dk ,
1 0.02731918655787 2.73191865578708 0.01363682732803 2 0.00271964142253 2.71964142253278 0.00135959407374 3 0.00027184177471 2.71841774707848 0.00013591861944 4 0.00002718295420 2.71829541991231 0.00001359145326 5 0.00000271828319 2.71828318698653 0.00000135852748 6 0.00000027182820 2.71828196396484 0.00000013550580 7 0.00000002718282 2.71828177744737 -0.00000005101167 8 0.00000000271828 2.71828159981169 -0.00000022864736 9 0.00000000027183 2.71827893527643 -0.00000289318262 10 0.00000000002718 2.71827005349223 -0.00001177496681 11 0.00000000000272 2.71827005349223 -0.00001177496681 12 0.00000000000027 2.71338507218388 -0.00489675627516 13 0.00000000000003 2.66453525910038 -0.05374656935867 14 0.00000000000000 2.66453525910038 -0.05374656935867 15 0 0 -2.71828182845905
Yi定程度时,公式的分子出现相近数相减,同Shi分母趋于零,舍入误差导致有效数字位数急
Ju减少,也同样导致求解精度的降低(
Er、Taylor展开法
f(x)设函数充分光滑,对于给定的步长,Li用 Taylor公式有 h
,,,,,f(x)f(x)23,f(xh)f(x)f(x)hhh ,,,,,,? (6.9) 2!3!
,,,,,f(x)f(x)23,f(xh)f(x)f(x)hhh ,,,,,,? (6.10) 2!3!
Cong而可建立数值微分公式
f(x,h),f(x)f(x,h),f(x),f(x),,O(h), (6.11) hh
O(h)O(h)其截断误差为(类似地,可Yi建立另一截断误差为数值微分公式
f(x),f(x,h)f(x),f(x,h),f(x),,O(h), (6.12) hh
2O(h)如将式(6.9)和式(6.10)相减,可建立截断误差为数值微分公式
95
f(xh)f(xh)f(xh)f(xh),,,,,,2,f(x)O(h) (6.13) ,,,2h2h
2,,O(h)类似地,将式(6.9)和式(6.10)相加,可得截断误差为的计算的Shu值微分公式 f(x)
f(x,h),2f(x),f(x,h)f(x,h),2f(x),f(x,h)2,, (6.14) f(x),,O(h),22hh
Ruo利用更多点处的函数值(如)的Taylor展开式的线性组合,将可建(x,2h),(x,3h),?
Li具有更高阶的截断误差的数值微分公式(
San、Richardson外推法
*S(h)假设利用某种数值方法得到某一量Yu步长有关的近似值,截断误差为 Sh
ppp*k12S,S(h),ah,ah,?ah,? (6.15) 12k
0,p,p,?,p,?p,a(i,1,2,?)a,a,?式中,系数非零,且均是与Bu长无h12kii12
关的常数(
Yong代替上述公式中的步长,得 h/2h
ppp12khhhh,,,,,,,,* (6.16) ,,,,?,,?SSaaa,,,,,,,,12k2222,,,,,,,,
Ru将上述两式进行加权平均,有望消去误差级Shu中的第一项,得到精度更高的数值计算
Gong式(如在式(6.15)中,取
fxhfxh()(),,,*, SfxSh,,(),()2h并且根据
(5),,,fxhfxhfxfx()()()(),,,24,fxhh(),,,, (6.17) 23!5!h
可得
(5),,,fxhfxhfxfx()()()(),,,*24,SShfxhh,,,,,,,()() (6.18) 23!5!h
Ruo将式(6.18)中的用替代,有 h/2h
hh24fxfx()(),,,(5),,,hfxhfxh()(),,,,,,*22,SSfx,,,,,,,() (6.19) ,,,,,,23!25!2h,,,,,,
96
2将以上两式线性组合,并消去的系数得 h
hh()()fx,,fx,41()()fx,h,fx,h422, ()()fx,,,Oh332hh
4h1**4 (6.20) ,S(),S(h),O(h)323
Zhe是Richardson外推算法的第一步(当然若有必要,还可以对式(6.20)继Xu进行外推运算
4O(h)(将式中的写成按幂次展开的形式)( h
2,f(x),xcosx例6.2 设,试YongRichardson外推法建立的数值公Shi(6.20)计算f(1.0)的
Jin似值(外推3次),初始步长取(计算结果Jing确到小数点后7位( h,0.1
Jie 计算结果见表6.2(
Biao6.2 例6.2计算结果
(6.12)式计算结果 第一次外推 第二Ci外推 第三次外推 h
0.1 0.22673616
0.05 0.23603092 0.23912917
0.025 0.23835774 0.23913335 0.23913363
0.0125 0.23893964 0.23913361 0.23913363 0.23913363
?6.3 Newton -Cotes Qiu积公式
bI(f),f(x)dx由高等数学的知Shi知,定积分定义为如下和式的极限 , a
n
(x,x)f(,) ,i,1iii,0
axxxbxxin,,,,,,,,, [,](0,1,,1),式中,极限过程为Zui大的子区间长011niii,
Du趋于0(这个定义本身就给出了一种计算积Fen近似值的方法(数值积分实际上就是用一些
Dian处函数值的线性组合来近似计算定积分,即
nn bI(f),f(x)dx,Af(x),E[f],Af(x) (6.21) ,,iiii, ai,0i,0
nnf(x)E[f]式中称为求积系数,称Wei求积节点,它们均与被积函数无关,表示,,,,Axii,0,0ii
97
Qiu积余项,也称为求积公式的截断误差(追求Li想的求积公式自然是希望其精确程度最高(
Gai括起来,数值积分需研究如下三个问题
(1) 求积公式的具体构造;
(2) 求积公式的精确程度衡量标准;
(3) 求积公式的误差估计;
Zhe里通过引入被积函数的插值函数以及求积公Shi代数精度的概念分析上述三个问题(
Yi、插值法建立求积公式
n设给定的个互异节点为,关于这些节点做被Ji函数的Lagrange 插,,n,1x,[a,b]i,0i
L(x)值函数,于是有 n
n,1,,,f()f(x),L(x),,(x) (6.22) nn,1,(n1)!Dui式(6.22)两端在积分区间[a,b]Shang积分,得
,,,n1 b b b,()f()()()fxdxLxdxxdx,,,nn,1,,, a a a (,1)!n
,,,n1n b b,f() ,f(x) l(x)dx,,(x)dx (6.23) ,,kkn1,, a a,(n1)!,k0
bnl(x)L(x)dx其中为关于节点DeLagrange插值基函数, 取作为积Fen的近似值,构,,xkni,0,i a造Chu插值型求积公式
n bf(x)dx,Af(x) (6.24) ,kk, ak,0
其中求积系数
bA,l(x)dx (6.25) kk, a
Tong时,求得该求积公式的求积余项为
,,,n1 b,f()E[f],,(x)dx (6.26) ,n1, a,(n1)!二、Newton -Cotes 求积公Shi
98
Jiang节点等距分布时建立的插值求积公式称为Newton -Cotes 求积公式(它的Si想最早出现于1676年Newton 写GeiLeibnitz(莱布尼茨) 的信中,Hou来Cotes(柯特斯) 对Newton 的方法进行了系统研究,于1711年给出Liao点数的所有公式的权(下面列出几个最简单、,10
Zui著名的Newton -Cotes 求积Gong式
(1) 用区间中点做零次插值多项式,得到Yi点Newton -Cotes 求积公式,称为中点求积公式,即
bab,,,()():()fxdxbafMf,,, (6.27) ,,, a2,,
(2) 用区间两个端点做一次插值多项式,De到两点Newton -Cotes 求积Gong式,称为梯形求积公式,即
bba, (6.28) ()(()()):()fxdxfafbTf,,,, a2
(3) 用区间两个端点及中点做二次插值多Xiang式,得到三点Newton -Cotes 求积公式,称为Simpson(辛普森)Qiu积公式,即
b,,baab,,,,,, (6.29) ()()4():()fxdxfaffbSf,,,,,,,,,,, a62,,,,,,
(4) 将区间四等分得到的五个节点(包括Qu间两个端点)做四次插值多项式,得到五点Newton -Cotes 求积公式,称WeiCotes 求积公式,即
bfxdx(),, a
(6.30) baababab,,,,,,33,,,,,,7()3212327() :()faffffbCf,,,,,,,,,,,,,90424,,,,,,,,
Guan于更详细的Newton -Cotes Qiu积公式的求积系数,可以查表6.3得到(
11例6.3 试分别用一点、二点、三点、四点以及五点Newton -CotesGong式计算积分dx, 01,x的近似值(计Suan结果取5位小数)(
Jie 利用中点求积公式,得
,,
,, 111 dx,1,,0.66667,,, 011,x,,1,,,2,,
Li用梯形求积公式,得
1111,,dx,,1,,0.75000 ,,, 01,x22,,
Li用Simpson求积公式,得
99
Biao6.3 Newton -Cotes Qiu积公式系数
,,nn A i
111
22
1412
666
31133
8888
323277124
9090909090
1975505075195
288288288288288288
412727412162722166
840840840840840840840
7513577132329892989357775113237
1728017280172801728017280172801728017280
,45409895888,9281049610496,92858889898
283502835028350283502835028350283502835028350
…… ……
,,
,, 11111 dx,,1,4,,,0.69444,,, 011,x62,,1,,,2,,利用四点Newton -Cotes求积公式,得
,,
,, 111111 dx,,1,3,,3,,,0.69375,,, 0121,x82,,1,1,,,33,,利用Cotes求积公式,得
,,
,, 1111117 dx,,7,32,,12,,32,,,0.69317,,, 01131,x902,,1,1,1,,,424,,事实上原积分的准确值为
11 dx,,ln0.693152, 01,x
Ke见这五个公式的近似积分的精确程度不同,Qiu积节点越多,得到积分近似值越精确(
100
三、代数精度
[9]由Weierstrass(维尔斯特La斯)多项式逼近定理可知,对任意给定的精Du要求,闭区间上的连续函数都可以用多项式Jin似(一个很自然的做法就是用精确积分的被Ji多项式的次数做为求积公式精确程度的度量(
Ding义6.1 若求积公式对于任意的不高于mCi的代数多项式做为被积函数时都精确成立,
1次多项式被积函数不精确成立,则称该求积Gong式具有m次代数精度( 而对某个m,
You(6.26)式可知,n,1个求积节点的Cha值型求积公式的代数精度至少为n(
2m容易证明,求积公式具有m次代数精度的Chong要条件是它对于都准确f(x),1,x,x,?x
m,1成立,而对于不准确成立( f(x),x
Tong过代数精度的定义容易验证,中点公式、Simpson公式、Cotes 公式的代数Jing度分别为1阶、3阶、5阶,但它们分别用Dao的是具有1个、3个以及5个求积节点的Newton -Cotes公式(从中可以看Dao这样一个规律:当插值节点的个数是奇数时DeNewton -Cotes求积公(n,1)
[6]式的代数精度至少为阶,其证明见参考Wen献( n,1
Li用代数精度的定义也可以确定数值积分公式Zhong的相关参数,目标是使求积公式的代数
21,x,x,?精度尽可能高(只需要依次Qu被积函数为,并通过使求积公式准确成立来Jianf(x)
Li适当数目的方程,进而求解未知参数(
Li6.4 试确定参数A,B,C,使得求积Gong式
2f(x)dx,Af(0),Bf(1),Cf(2) , 0
De代数精度尽可能高(
2f(x),1,x,x解 根据代数精度的Ding义,令时,求积公式精确成立,得
A,B,C,2,
,B,2C,2 ,
,B,4C,8/3,
解之得
141A,,B,,C, 333
3,,fx,x取,则
101
23 xdx,4, 0
413 ,,,,Af0,Bf1,Cf(2),,,2,433
Ci时,该求积公式至少具有3次代数精度(
4,,fx,x取,有
2324 xdx,, 05
但是
4120401(2)2,,,, Af,Bf,Cf,,,,333
42因此,当A,0,B,,C,时,求积公Shi达到最高的代数精度,且代数精度的次数为3次( 33
Li6.4实际上是积分区间取[0,2]时的Simpson求积公式(可以看到,在固定Qiu积节点的情况下,用待定系数法得到的求积Xi数和用插值法建立的求积公式的求积系数是Xiang同的(这是因为,用待定系数法建立的形如Shi(6.21)的求积公式至少具有n次代数Jing度,而至少具有n
[6]次代数精度的求积公式一定是插值型的(
Si、Newton -Cotes求积公式的Jie断误差
f(x)[a,b]定理6.1 设函数在Ji分区间上具有连续的二阶导数,则中点求积Gong式的截断误差为
3()ba,,,,,Effab[]() (),,, (6.31) M48
Zheng明 由Taylor展开公式
2,,abababfab(),,,,,,,,,,,,,, fxffxxab()(),,,,,,,,,,,,,,,,2222!2,,,,,,,,
[a,b]对上式两端在区间上积分,有
2 b b,,(),,abfab,,,,,()()fxdxxbafxdx ,,,,,,,,,, a a22!2,,,,
2a,b,,,,g(x),x,[a,b]f()[a,b],由于函数在积分区间内不Bian号,而函数在上连,,2,,
102
Xu,由积分第二中值定理知,在内存在一点,Shi得 (,)ab,
23b ,,,f()a,b(b,a),,,, E[f],x,dx,f(,),,M,a 2!248,,
Ding理6.2 设函数在积分区间上具有连续De二阶导数,则梯形求积公式的截断f(x)[a,b]
误差为
3()ba,,,,,Effab[]()(),,,, (6.32) T12
证明 梯形求积公式的余项为
b,,f(), Efxaxbdxab[]()() (),,,,,,T, a2!
,,由于,(x),(x,a)(x,a)在Ji分区间内不变号,而函数在上连续,[a,b]f(,)[a,b]2
You积分第二中值定理知,在(,)ab内存在Yi点,使得 ,
3b ,,,f()(b,a),,E[f],(x,a)(x,b)dx,,f(,) T,a 2!12
f(x)[a,b]定理6.3 设函数在Qu间上有连续的四阶导数,则SimpsonGong式的截断误差为
5()ba,(4),,Effab[]()(),,,, (6.33) S2880
H(x)[a,b]f(x)证明 对区间上De函数,构造次数不高于3次的插值多项式,Shi得 3
H(a),f(a), H(b),f(b) 33
a,ba,ba,ba,b,,,,,,,,,,, H,fH,f ,,,,,,,,332222,,,,,,,,不难得到
2,,4,f()a,b,,f(x),H(x),(x,a)x,(x,b) a,,,b ,,34!2,,
[a,b]对上式两端在区间上积分
103
24,, b b bf()a,b,,, f(x)dx,H(x)dx,(x,a)x,(x,b)dx,,3,,, a a a4!2,,
YinSimpson公式的代数精确度是3,所Yi
b,,,,b,aa,b,,f(x)dx,,H(a),4H,H(b),,,,,333,,, a62,,,,,,
2,,4 bf()a,b,,, ,(x,a)x,(x,b)dx,,, a4!2,,
,,,,b,aa,b,, ,,f(a),4f,f(b),,E[f],,,,S,,62,,,,,,
式中
24,,, bf()ab,,,E[f](xa)x(xb)dx,,,,,,S, a4!2,, 2,,45 b,f()ab(ba),,,,,,4(xa)x(xb)dxf(,),,,,,,,,, a4!22880,,
Ding理6.3所使用的证明方法也可以用来证明Ding理6.1(对于更为复杂的Cotes 公Shi,有
Ding理6.4 设函数f(x)在区间[a,b]上有连续的6阶导数,则Cotes 公Shi的截断误差为
62()baba,,,,6,, (6.34) ,,Effab[]() (),,,,4,,9454,,
Wu、Newton -Cotes 求积公式De稳定性和收敛性
Ben节简要分析Newton –Cotes公Shi序列的收敛性及稳定性(
Ding义6.2 Newton -CotesQiu积公式的收敛性是指,对于任意连续的被积Han数,当求积节
n,,点的个数时,截断误差序列满足( limE[f],0n,,n
n,,Newton -Cotes 求积公Shi是基于等距插值建立起来的,但因当时,插Zhi函数不保证收敛到被插值函数,进而也不能Bao证( limE[f],0n,,n
f(x)Newton -Cotes求积公Shi序列的稳定性主要考虑函数值计算的舍入误Cha对数值积分i
结果的影响(
,,ef(x)If()定义6.3 对于一Ge求积公式序列,假设在计算时,引入舍入误Cha,,,iin0n,
~即有,并记 f(x),f(x),eiii
104
nn~~I(f),Af(x),I(f),Af(x) ,,niiniii,0i,0
Ru果对任意给定的小正数,只要误差充分小,Jiu有 ,,maxe,,0ii
n~~ I(f),I(f),A[f(x),f(x)],,,nniiii,0
,,则称该求积公式序列是稳定的( If(),,n0n,
对于数值求积公式,有
nnnn~ A[f(x),f(x)],Ae,Ae,A,,,,,iiiiiiii,0,0,0,0iiii
You于Newton -Cotes求积公式对Chang数均能精确积分,当被积函数时,有 f(x),1
n
An,,在的过程中,Newton -Cotes求积公式序列的求积系数有正有负,的You界性不,ii,0能保证,因而Newton -Cotes求积公式得稳定性不能保证(
Ji于上述稳定性、收敛性原因,在实际计算中,人们并不追求高阶的Newton -Cotes 求积公式,而是通过细化积分区间的Fang法,用复化求积公式来提高数值积分的精度(
?6.4 复化求积法
Cong积分的定义可以看出,增加求积节点数目可Yi提高数值积分的代数精度(但通过增加插值Jie点建立的高阶Newton -CotesQiu积公式的稳定性差(一种提高求积精度的方Fa是先将整个积分区间细分,然后在每个小的Qu间上使用低阶的Newton -Cotes 求积公式,这就是复化求积法(理论和数Zhi结果都表明,这种方案可以获得理想的数值Jie果( 一、复化梯形公式
b,anh,[a,b]首先将积分区间 等Fen,区间长度,节点记为n
xaihin,,, (0,1,,)[x,x],然后在每个小区间上使用梯形公式,De ii,1i
105
n,1 b xi,1f(x)dx,f(x)dx,,, a xii,0
3n,1hh,,, ,[(f(x),f(x)),f()],ii,1i212i,0
3n,1n,1hh,,,,,f(a),2f(x),f(b),f(,),,,,ii212i,1i,0,,略去上式最后一项,De到复化梯形公式
n,1h,, (6.35) Tf(a)2f(x)f(b),,,,,,ni2,,i,1其截断误Cha为
3n,1h,,,,,,() (),,Efxx ,Tiiii,1n12i,0
Ding理6.5 设函数f(x)在积分区间[a,b]上具有连续的二阶导数,则复化梯形公Shi的截断
误差为
ba,2,, (6.36) () (),,Ehfab,,,,Tn12
,,mf(x)[a,b]证明 因为在上连Xu,则其在区间一定有最大值和最小值,即 M
,,mfMxxab,,,,(),(,)[,],, iiii,1进而有
n,11,,m,f(,),M ,ini,0
,,,,a,b由连续函数的介值定理知,存Zai一点,使得
n,11,,,,f,(),f(,) ,ini,0故
3n,1hb,a2,,,,E,,f,(),,hf(,) ,Tin12120i,
Cong截断误差可以看出,复化梯形公式的代数精Du仍为一阶(
106
Er、复化Simpson公式
Ruo在每个小区间上使用Simpson公式,You
n,1 b xi,1f(x)dx,f(x)dx,,, a xii,0
5n,1n,1,,,,hh,,4,,,,,,f(x),4fx,f(x),f() ,,i1i,1i,,,,i,62880i,0i,0,,2,,
5n,1n,1n,1,,,,hh,,4,,,,,f(a),2f(x),4fx,f(b),f(,),,,i1i,,,,i,62880i,1i,0i,02,,,,上Shi略去最后一项,得到复化Simpson公Shi
n,1n,1,,,,h,,,,S,f(a),2f(x),4fx,f(b) (6.37) ,,ni1,,,,i,6i,1i,0,,2,,其截断误差Wei
5n,1h4,,Efxx,,,,() (),, ,Siiii,1n2880i,0
,,,,fxa,b定理6.6 设函数在Qu间上有连续的四阶导数,则复化Simpson公式的截断误差为
ba,4,,4() (),, (6.38) Ehfab,,,,Sin2880
Cong截断误差可以看出,复化Simpson公Shi的代数精度仍为三阶(
Dui于上节的中点求积公式,使用同样的方法,Ye可以获得其对应的复化求积公式以及截断误Cha
n,1,,Mhfx,,,,n1i,i,02,,
ba,2,,() (),,Rhfab,,,Mn48
[6]可以证明这三个复化求积公式都是收敛De、稳定的(
,/2cosxdx例6.5 使用复化梯Xing公式和复化Simpson公式计算定积分De近似值时,要, 0
,5求误差不超过10,分别需要多少个求积Jie点,
107
,,ba,,,解 这里,( , , max1bahf,,,,,,,,ab,,,22nn
,5从复化梯形公式的截断误差可知,要使得Jin似值的误差不超过,则需满足 10
b,a2,5,,,,max,hf,,10 a,b,,12
解不等式得
n,179.7170
Qu,相应的需要个求积节点; n,180n,1,181
Tong理,用复化Simpson公式计算时,需Man足
b,a4(4),5,,max,hf,,10 a,b,,2880
4,b,a,,,5(4),,10,,由于maxf,,1,解得,,因此,需要将区间Jin行n,4.2688,,a,,,b28802n,,
Deng分,相应的需要个求积节点( n,52n,1,11
San、区间逐次分半求积法
Shi用复化求积公式计算积分值,要保证满足指Ding精度,依据截断误差,需要将中值定理使用Shi产生的被积函数的高阶导数在某一点的绝对Zhi放大为整个积分区间上的最大值,若,
Zui大值难求,还需进一步进行放大运算,势必Dao致过多地选取求积节点,影响计算效率(
Qu间逐次分半求积法则避免了这种不便(它是Gen据规定的精度要求,在计算过程中把积分区Jian逐次分半,利用相邻两次求积结果之差来判Bie误差的大小,从而得到满足精度要求的积分Jin似值(下面以复化梯形公式为例来说明区间Zhu次分半求积法的计算过程(
2n由复化梯形公式的误差估计式可以看到,(当对较大时,可以认为 E,O(h)Tn
2 (6.39) E,chTn
c这里为常数,当将区间等分时有 2n
2h,, (6.40) E,c,,T2n2,,
进而
IT,n,4 (6.41) I,T2n
即
108
1 (6.42) I,T,(T,T)2n2nn3
1T作为准确值I的近似值时,误差大约为(Yin此可以使用上式说明,若用(T,T)2n2nn31(T,T),,T,判断近似值的Jin似程度,其中为容许误差,这样就避免了被Ji函数高2nn2n3
Jie导数最值的估计(
T需要指出的是,在实际计算时,由于每次总Shi在前一次对分的基础上将区间再次对分,2n
Fen点加密一倍,原分点上的函数值不需要重复Ji算,这样可以采用如下的递推公式减少计算
量
nThba1,,,,,n (6.43) Tfaihh,,,,,,,,,,,2n,,n222,,,1i,,
Tong理,也可以类似的给出基于复化Simpson公式和复化Cotes 公式的区间逐次Fen半求积
法,此时有
1 (6.44) I,S,(S,S)2n2nn15
1 (6.45) I,C,(C,C)2n2nn63算法6.1 (复化梯形求积算法)
,a,b输入 区间端点及精度;
Shu出 积分近似值; T
T,h(f(a),f(b))h,(b,a)/2Step 1 令,,,; n,1hh,/20
i,1,2,?,nF,F,f(a,(2i,1)h)Step 2 令,对,计算; //计算新节点函数值和 F,0
T,T/2,hFStep 3 计算; //计算式(6.43) 0
n,2n,h,h/2,T,TStep 4 若,算法终止,输出;否则,赋值,转Step2( TT,T,,00
Suan法6.2 (复化simpson求积算法)
,a,b输入 区间端点及精度;
Shu出 积分近似值; S
109
,,Step 1 令,; h,b,a/4n,2
,,FfafbFfab,,,,()(),(()/2),S,b,a(F,4F)/6Step 2 计算,; hh,/200101
,,Step 3 令,对,计算;//计算Xin节点函数值和 F,0F,F,fa,(2i,1)hi,1,2,?,n222
S,h(F,2F,4F)/3Step 4 计算; 012
n,2n,h,h/2,S,SStep 5 若,算法终止,输出;否则,令, S,S,,S00
F,F,F转Step3( 223
1sinx例6.6 使用复化梯形公式和Fu化Simpson公式计算定积分的近似值,要求误dx, 0x
,5差不超过( ,,10
Jie 使用区间逐次分半求积法的复化梯形公式He复化Simpson公式进行求解(计算结Guo如
kh,(b,a)/2表6.4所示,其中等Fen区间间距为:,算例使用 和T,T,,S,S,,2nn2nn
Zuo为误差终止判断条件(
Biao6.4 例6.6的计算结果
Fu化梯形公式近似值 复化Simpson公Shi近似值 k
0 0.9207355
1 0.9397933 0.9460869
2 0.9445135 0.9460833
3 0.9456909
4 0.9459850
5 0.9460586
6 0.9460769
7 0.9460815
?6.5 Romberg求积法
Yi、Romberg求积法
11ST(T,T)(S,S)区间逐次分半Qiu积法将或处理成误差,将或作为积分2n2n2nn2nn315
110
T(S)T(S)的近似值(分析近似表达式(6.45)和(6.47)后可以发现,既Ran和都已经算出,nn2n2n
111或也可以算出,那么将或自然地,误差(T,T)(S,S)T,(T,T)2nn2nn2n2nn3315
1整体作为积分的近似值,显然可进一步改善Ji分计算精度( S,(S,S)2n2nn15
事实上,可以验证
1 (6.46) T,(T,T),S2n2nnn3
Shang式表明对基于区间逐次分半求积的复化梯形Gong式进行误差校正得到复化Simpson求Ji公式
24O(h)O(h)的计算值,从而把误差Cong提高到(
类似地,有
1 (6.47) S,(S,S),C2n2nnn15
Ji对基于区间逐次分半求积的复化Simpson公式进行误差校正得到复化Cotes求Ji公式的计
46O(h)O(h)算值,误差从提高到(
Wo们称基于区间逐次分半求积的复化Cotes公式进行误差校正得到的公式为Romberg(龙贝格)求积公式
1 (6.48) C,(C,C),R2n2nnn63
8O(h)它的误差阶是(
Er、Richardson外推法
Romberg求积算法还可以通GuoRichardson外推技巧得到(文献[4]给出了复化梯形公式的渐近展开形式的Wu差表达
b246fxdxTahahah(),,,,, (6.49) n246, a
a,a,a?其中,是与步长无关的常数( h246
,,使用基于复化梯形公式的区间逐次分半求Ji法,可得梯形序列T( ,,nn1,
Xian将Richardson外推技巧用到式(6.49),经过一次外推得到
111
b41(1)4(1)6 (6.50) fxdxTTahah,,,,,()246nn, a33
41,于是有 而由式(6.46)知STT,,nnn233
b(1)4(1)6 (6.51) fxdxSahah(),,,,46n,a
Zhe与定理6.6一致(
Lei似地使用Richardson外推技巧,Huan可以依次得到式(6.47)和式(6.48) ( 算法6.3(Romberg算法)
,输入 积分区间端点参数及精度; a,b
Shu出 积分近似值;
Step 1计算初值; Tbafafb,,,()()/2,,,,1
ba,iStep2 令,按式 (6.43) 计算梯形序列; (1,2,;2)hin,,,T,,nn
Step 3 分别按式 (6.46) 、Shi (6.47)、 式 (6.48) 计Suan序列、、; SCR,,,,,,nnn
Step 4若,算法终止,输出Rn(2);否则,区间分半,转Step2( RnRn(2)(),,,
14,7dx例6.7 使用Romberg求积法计算定积分的近似值,要求误差不超Guo. ,,10,2 01,x
nh,(b,a)/2解 计算结果如表6.5所示,其中等分区间间距为:,算例使用
Zuo为误差终止判断条件( R,C,,nn
Biao6.5 例6.7的计算结果
n 梯形序列(I (n,0)) Simpson序列(I (n,1)) Cotes 序列(I (n,2)) RombergXu列(I (n,3))
0 3
1 3.10000000 3.13333333
2 3.13117647 3.14156863 3.14211765
3 3.13898849 3.14159250 3.14159409 3.14158578
4 3.14094161 3.14159265 3.14159266 3.14159264
容易计算
14dx,,,3.1415926535897?? ,2 01,x
Ke以看到,当时,使用基于复化梯形公式的区Jian分半求积法,误差是 k,4
112
,,3.1409416,0.0006510??
Dan是通过外推之后,得到的龙贝格序列的误差Jian小为
,,3.14159264,0.00000001??
Ji算精度得到了很大提高(
?6.6 Gauss型求积公式
Qian面研究的数值求积公式都是在积分区间内事Xian确定了个求积节点,然后通过待定n,1
Xi数法,按照使求积公式的代数精度达到最高De原则选取最佳求积系数(和通过插值的方法De到的求积系数是一致的)(已经知道,对于Ju有个求积节点的求积公式,其代数精度n,1
n至少可以达到次(那么能否适当地选择求积Jie点的位置和相应的求积系数,使得求积公式Ju有更高甚至最高的代数精度,答案是肯定的(例如下面的求积公式
,,,, 133,,,,,,fxdx,f,,f ,,,,,, 133,,,,
Ke以验证,该公式的代数精确度是3次,而前Shu的两点Newton -Cotes公式即Ti形求积公式的代数精度只能达到1次(
n{x}实际上,对任意一组个互异求积节点De插值型求积公式,当被积函数n,1,0ii
f(x)取为次的多项式 2n,2
2222 ,,,,,,,(x),x,xx,x?x,xn,n101
时,总有
nb 22I(f),,(x)dx,A,(x),E[f],E[f],0 (6.52) ,n,in,i11,a i,0
Ji对任意的个互异求积节点构造的求积公式的Dai数精度不能达到次,那么是否能n,12n,2够达到次,则是本节考虑的问题( 2n,1
Yi、Gauss型求积公式
Yi般地,如果选取个求积节点,要使求积公式Dui任意的次多项式精确成立,n,12n,1Gen据待定系数法,有
113
b,AAAdxba,,,,,101n, a,
22, bba,,AxAxAxxdx,,,,0011nn,, a2 (6.53) ,
,
,,,2222nn bba,,,,,21212121nnnn,AxAxAxxdx,,,,0011nn, a,22n,,
Li论上可以证明,上述非线性方程组的解是存Zai惟一的(也就是说,通过合理地选取求积节Dian及求积系数,可以使得求积公式的代数精度Da到次(将这种具有个求积节点的2n,1n,1具有次代数精度的求积公式称为Gauss型求积公式,对应的一组求积节点称为一组2n,1
Gauss点(
Gauss型求积公式的求积节点和求积系数Ke以通过求解非线性方程组(6.53)得到,然而,直接求解该非线性方程组是复杂的(Tong常构造Gauss型求积公式的方法是,首Xian通过正交多项式确定一组Gauss点,然Hou再使用待定系数法或插值的方法求出Gauss型求积公式的求积系数(
n{x}定理6.7 对于插值型求积公式,其互异节点是一组Gauss点的充分必要Tiao件是以,0ii
,()()()()xxxxxxx,,,,Zhe些点为零点的多项式函数与任意的次数不超Guon次的nn,101
,,a,b多项式函数在积分区间上正交,即Man足 p(x)
b (6.54) ,(x)p(x)dx,0n,1,a
Zheng明 (充分性) 对任意不超过2n+1Ci的多项式g(x),存在不超过n次的多项Shi和q(x)r(x),使得
g(x),q(x),(x),r(x) (6.55) n,1
Cheng立(对上式两端积分,得
bbbb (6.56) g(x)dx,q(x),(x)dx,r(x)dx,r(x)dxn,1,,,,aaaa
n{x}对互异节点组,构造插值型求积公式,即取求积系数 ,0ii
114
nx,xbj (6.57) A,dx(k,0,1,?,n),k,ax,x,0jkj ,jk
Zhe样求积公式至少具有n次代数精度(
利用代数精度概念有
nnbr(x)dx,Ar(x),Ag(x) (6.58) ,,iiii,a,0,0ii
Bi较式(6.56)和式(6.58),有
nbg(x)dx,Ag(x) (6.59) ,ii,ai,0
Zhe样求积公式具有2n+1次代数精度,积分Jie点是一组Gauss点(
nn{x}{A}是一组Gauss点,是相Ying的Gauss求积系数,这样的求积公(必Yao性) 节点,0,0iiii
p(x),(x)式具有2n+1次代数精度(设是任意不超过n次的多项式,不超过2n+1次( p(x)n,1
nbp(x,)(x)dx,Ap(x),(x),0 (6.60) ,n,1iin,1i,ai,0
Zhe说明式(6.54)成立(
[a,b]由定理6.7可知,只要能够找到Yu任意的次数不超过n次的多项式函数p(x)在区间上正交的n+1次多项式函数,那么,这个函数的所有零点即为Gauss点(下Mian以Legendre (勒让德) 多项式Wei例,介绍Gauss型求积公式的构造过程(
Er、Gauss-Legendre求积公式
称形如
n 1f(x)dx,Af(x) (6.61) ,ii, ,1,0i
DeGauss型求积公式为Gauss-Legendre求积公式( 可以证明,该求积Gong式对应的n+1个Gauss点正好是n+1次勒让德多项式
n,11d2n,1 (6.62) p(x),(x,1)n,1n,1n,1(n,1)!2dx
115
De一组零点(在求得一组Gauss求积节点Hou,求积系数可通过待定系数法或插值型求积Gong式
De求积系数公式求得(表6.6给出了部分Gauss-Legendre求积公式的求积Jie点和求积系数(
Biao6.6 Gauss-LegendreQiu积公式中的数据
Ax n kk
0 0 2
1 ?0.5773502692 1
?0.7745966692 0.5555555556 2 0 0.8888888889
?0.8611363116 0.3478548451 3 ?0.3399810436 0.6521451549
?0.9061798459 0.2369268851
4 ?0.5384693101 0.4786286705
0 0.5688888889 和上一节描Shu的求积公式不同的是,Gauss-Legendre求积公式的积分区间是[,1,1],对于
bf(x)dx定积分,可以通过变量代换 , a
a,bb,ax,,t (6.63) 22
[a,b][,1,1]将区间上的积分转化Wei上的积分
b 1baabba,,,,,f(x)dxftdt,, (6.64) ,,,,, a 1222,,
Ran后再使用Gauss-Legendre求Ji公式进行计算(
Li6.8 分别使用两点Gauss-Legendre求积公式和四点Gauss-Legendre求积公式计算定
,/2cosxdx积分的近似值( , 0
,x,(1,t)解 作变量代换,则 4
,/2 1,,,,Icosxdxcos(1t)dt,,, ,,,,, 0 144,,
116
,,,(t),cos(1,t)t,0.5773503A,A,1记,因为节点,,,Yout,,0.5773503,,,00114,,
Liang点Gauss-Legendre求积公式De
, I,(,(t),,(t)),0.9984726016014
t,0.8611363116t,,0.8611363116同样地,取,,t,0.3399810436,012
t,,0.3399810436A,A,0.347854845A,A,0.6521451549,,,由四点30123
Gauss-Legendre求积公式得
, I,(A,(t),A,(t),A,(t),A,(t)),0.9999999772001122334
,/2易知,I,cosxdx,1(四点Gauss-Legendre求积公式的误Cha为 , 0
,7 1,0.9999999772,10
,5而由例6.3可知,要求误差不超过,复Hua梯形公式和复化Simpson公式分别需Yao181个10
Qiu积节点和11个求积节点(可见,Gauss型求积公式具有较高的计算精度(但是,当Qiu积节点数目增加时,Gauss点发生了变Hua,前面计算的函数值不能在后面使用( 三、Gauss型求积公式的截断误差及稳定性
Ding理6.8 设被积函数f(x)的2n+2Jie导函数在区间[a,b]上连续,则Gauss求积公式的截断误差为
,(2n2)b,f()2R[f],(,(x))dx,,(a,b) (6.65) ,1n,a(2n,2)!
H(x)证明 设是满足如下插值条件的不Chao过2n+1次的插值多项式 2n,1
H(x),f(x),2n,1kk (6.66) (k,0,1,?,n),,,H(x),f(x)2n,1kk,
Ze其插值余项可表示为
117
n,(22),f()2 (6.67) f(x),H(x),(,(x)),,(a,b)n,n,211(2n,2)!由于Gauss型求积公式具有次代数精度,因此 2n,1
nnbH(x)dx,AH(x),Af(x) (6.68) ,,2,12,1niniii,a,0,0ii故,求积公式截断误差可以表Shi为
nbR[f],f(x)dx,Af(x) ,ii,a,0i
bb ,f(x)dx,H(x)dx2,1n,,aa
,(22)nb,f()2 (6.69) ,(,(x))dx,1n,a,(2n2)!
2(,(x))因为在求积区间上不变号,的2n+2阶导函数在求积区间上连续,对式f(x)n,1
(6.69)使用积分第二中值定理便得到式(6.65) ( 对于Gauss型求积Gong式,其求积系数
nb22AAlxlxdx,,,(())(())0(6.70) ,kikk,ai,0
nn{l(x)}{x}其中,是以Gauss点为插值节点的Lagrange插值基函Shu(上式表明Gauss,0ii,0ii
Qiu积系数都大于零,进而得到如下定理
Ding理6.9 Gauss型求积公式序列是Wen定的、收敛的(
118
知识结构图
Cha值法建立数值微分公式
Taylor法建立数值微分公式 数值微Fen
Richardson外推法建立高阶数值微Fen公式
数
Cha值法建立求积公式 值
Wei 基本概念 代数精度 分 收敛性与稳定Xing 与
Shu 具体公式 值 代数精度 Newton-Cotes公式 积
分 截断误差
复化梯形公式
数值积分
Fu化求积公式 复化Simpson公式
Qu间逐次分半求积算法
Romberg求积公式
基本理论
Gauss-Legendre公式 Gauss型求积公式
Jie断误差 Gauss-Legendre公Shi
习题六
[x,2h,x,2h]x,x,khf(x)(2,1,0)k,,,1 设在区间上You连续的四阶导数, ,00k0
试证明
14,,,f(x),f(x),8f(x),8f(x),f(x),O(h)1) ; ,,0211212h
119
12,,2) ,,f(x),f(x),f(x),2f(x),O(h),01102h
2 已知函数的下列数据 f(x)
k 1.8 2.0 2.2 2.4 2.6 x
k f(x) 3.12014 4.42659 6.04241 8.03014 10.46675
,,,分别用一阶中点公式和二阶中点公式计Suan和的近似值( f(2.2)f(2.2)
,3 Archimedes(阿基米德)Tong过计算半径为1的圆的内切和外切正多边形De周长得到的近
n似值(边内切多边形的周长为
,,p,nsin,/n, n
n边外切多边形的周长为
,,q,ntg,/n, n
,这两个值分别给出了值的上下限(
pq1) 利用Taylor公式,证明和可Xie成如下形式 nn
24p,a,ah,ah,?,n012 24q,b,bh,bh,?,n012
a,b其中,(求出精确的( h,1/n00
p,3.0000,p,3.1058,,2) 设用Richardson外推法做一次Wai推,得到值的更好近612
q,3.4641,q,3.2154,,似(类似地,设用Richardson外推法Zuo一次外推,得到值612
的更好近似(
4 试建立如下一点数值求积公式
2b(b,a),f(x)dx,(b,a)f(a),f(,) 1)左矩形公式 1,a2
2b(b,a),f(x)dx,(b,a)f(b),f(,) 2)右矩形公式 2,a2
,,,,(a,b) 式中( 12
5 确定下列求积公式中的参数,使得其代Shu精度尽量高,并指明其代数精度(
120
h1) f(x)dx,Af(,h),Af(0),Af(h),101,,h
11 2)f(x)dx,[2f(x),3f(x),f(1)]12,,13
6 证明:Romberg阵列中第二列是Dui被积函数应用Simpson公式的结果,Ji验证式(6.46)(
27 要使积分的近似值具有6位有效数字,若用复化Simpson或复化梯形求积公Shilnxdx,1
Fen别需使用多少个节点处的函数值,
1,x8 用Romberg求积算法计算De近似值,使它具有5位有效数字( edx,0
9 利用Gauss求积公式和Newton-Cotes求积公式(都取四个求积节点)计算积分
11dx,201,x
De近似值,并比较结果(
14ln10 (数值实验) 已知积分,试Bi较如下三种方法计算该积分近似值时,若xxdx,,,09
,7要使结果的误差不超过,各调用了被积函Shu多少次, 10
Suan法1 基于区间逐次分半法的复化梯形公Shi;
算法2 基于区间逐次分半法的复HuaSimpson公式;
算法3 Romberg求积公式(
11 (数值实验) 用给定的方法求值
1,k,x1k,0,1,?,201)用Romberg求积公式计算积分,; I,exedxk,0
2)证明上述积分满足递推公式
I,1,kI kk,1
,1I,1,eIk,1,?,20从出发,Yong递推关系计算,的近似值; 0k
I,03)取,从出发,利用向后递推公式 k,20k
I,(1,I)/k k,1k
I求的近似值(用不同的做试验,观察对结果Jing度的影响( kk
12 (数值实验) 用数值微分公式(6.15)计算中点导数的近似值,试以求对数函Shu在0.01,lnx
2O(h)0.1,1,10处导数近似值为Li,分析计算精度随步长h的变化规律,误差Shi否和同
121
Jie,是否步长越小计算精度越高,
122
数值分析原理课件第二章
11
Di二章 非线性方程数值解法
Zai科学计算中常需要求解非线性方程
() 0f x = (2.1)
Ji求函数 () f x 的零点.非线性方Cheng求解没有通用的解析方法,常采用数值求解Suan法.数值解 法的基本思想是从给定的一个Huo几个初始近似值出发,按某种规律产生一个Shou敛的迭代序列
0{}k k x +∞
=,使它逐步逼近于方程 (2.1)的某个Jie.本章介绍非线性方程实根的数值求解算法:二 分法、简单迭代法、 Newton Die代法及其变形,并讨论它们的收敛性、收敛Su度等.
§2.1 二分法
一、实根的隔离
Ding义 2.1 设非线性方程 (2.1)中De () f x 是连续函数.如果有 *x 使 *() 0f x =,则称 *x 为方 程 (2.1)的根,或称为函数 () f x 的零点;如果有 *() () () m f x x x g x =-,且 () g x 在 *x 邻域内连 续, *() 0g x ≠, m 为正Zheng数,则称 *x 为方程 (2.1)的 m 重根.当 1m =时,称 *x 为方Cheng的单 根.
Fei线性方程根的数值求解过程包含以下两步
(1) 用某种方法确定有根区间.称仅存在Yi个实根的有根区间为非线性方程的隔根区 Jian,在有根区间或隔根区间上任意值为根的初Shi近似值;
(2) 选用某种数值方法逐步提高根的精度,使之满足给定的精度要求.
Dui于第 (1)步有时可以从问题的物理背景Huo其它信息判断出根的所在位置,特别是对于Lian 续函数 () f x ,也可以从两个Duan点函数值符号确定出有根区间.
Dang函数 () f x 连续时,区间搜索法Shi一种有效的确定较小有根区间的实用方法,Qi具体做 法如下
She [, ]a b 是方程 (2.1)的Yi个较大有根区间,选择合适的步长 () /h b a n =-, k x a kh =+, (0,1, , ) k n = .由左向右逐个计算 () k f x ,如果有 1() () 0k k f x f x +<,则区间 1[,="" ]k="" k="" x="" x="" +就是方程="">
Yi般情况下,只要步长 h 足够小,就能把Fang程的更小的有根区间分离出来;如果有根区 间足够小,例如区间长度小于给定的精度要Qiu,则区间内任意一点可视为方程 (2.1)的根的一 个近似.
Li 2.1 确定出方程 32() 3430f x x x x =-+-=的一个有Gen区间. 解 由 22() 3643(1) 10f x x x x '=-+=-+>知 () f x 为 (, ) -∞∞上的单调递增函数 ,进而 () f x 在 (, ) -∞∞内最多只有一个实根.经计算知 (0)0f <, (2)0f="">,所以 () 0f x =在区间 [0,2]内有惟一实根.
Ru果希望将有根区间再缩小,可以取步长 0.5h =,在点 0.5x =, 1x =, 1.5x =计算出函 数值的符号,Zui后可知区间 [1.5,2]内有一个实根.
12
二、二分法
Er分法是求非线性方程实根近似值的最简单的Fang法.其基本思想是将有根区间分半,通 过Pan别函数值的符号,逐步缩小有根区间,直到Chong分逼近方程的根,从而得到满足一定精度 Yao求的根的近似值.
She () f x 在区间 [, ]a b 上连续, () () 0f a f b <,且方程 (2.1)在区间="" (,="" )="" a="" b="" 内有惟一实根="" *x="" .记="" 1a="" a="," 1b="" b=",中点" 111()="" x="" a="" b="+将区间" 11[,="" ]a="" b="" 分为两个小区间="" 11[,="" ]a="" x="" 和="" 11[,="" ]x="" b="" ,计算函shu="" 值="" 1()="" f="" x="" ,根据如下="">
(1) 如果 1() 0f x =,则 1x 是所要求的根;
(2) 如果 11() () 0f a f x <,取新的有根区间 2211[,="" ][,="" ]a="" b="" a="" x=";" (3)="" 如果="" 11()="" ()="" 0f="" x="" f="" b=""><,取新的有根区间 2211[,="" ][,="" ]a="" b="" x="" b="">
Xin有根区间 22[, ]a b 的长度为Yuan有根区间 11[, ]a b 长度的一Ban.对有根区间 22[, ]a b 施以Tong样 的过程,即用中点 222() /2x a b =+将区间 22[, ]a b 再分为两半,选取新的有根区间,并记为 33[, ]a b ,其长度为 22[, ]a b 的一半 (如图 2.1所Shi ) .
Tu 2.1 二分法示意图
Zhong复上述过程,建立如下嵌套的区间序列
1122[, ][, ][, ][, ]k k a b a b a b a b =????
Qi中每个区间的长度都是前一个区间长度的一Ban,因此 [, ]k k a b 的长度Wei
11
()
2k k k b a b a --=-
由 *
[, ]k k x a b ∈和 () /2k k k x a b =+,得
*11
() () 22
k k k k x x b a b a -≤-=-
Dang k →∞时,显然,有 *
k x x →.总结得到如下收敛定理:
Ding理 2.1 设 () f x 在隔根区Jian [, ]a b 上连续,且 () () 0f a f b <>
0{}k k x +∞
=收敛于方程 (2.1)在 [, ]a b 上的根 *x ,并且有误差估计
*1
() (1,2, ) 2k k
x x b a k -≤
-= (2.2) 设预先给定根 *x 的Jue对误差限为 ε,要求 *k x x ε-≤,只要 1
() 2
k b a ε-≤成立,这样求
13
得对分次数
ln() ln ln 2
b a k ε
--≥
. (2.3)
Qu k 为大于 (ln() ln ) /ln 2b a ε--的最小整数.此时 k x 是方程 (2.1)的满足精度要求De根近似
值.
Zhu :由于舍入误差和截断误差存在,利用浮Dian运算不可能精确计算函数值,二分法中的 Pan断 () 0k f x =几乎不可能满Zu,取而代之为判断条件 0() k f x ε<,其中 0ε为根近似值的函数="">
Zong结以上内容,给出如下算法 算法 2.1 (二分法 )
Shu入 端点 , a b 、根的绝对误差Xian ε、根近似值的函数值允许误差限 0ε; 输出 近似解 c 或失败信息;
Step 1 用公式 (2.3)计算最大Die代次数 k ; Step 2 对 1, , n k = 循环执行 Step 3~5; Step 3 () /2c a b =+,计算 () f c ;
Step 4 若 0() f c ε<,ze输出 c="" ,="" end="" ;="" step="" 5="" 若="" ()="" ()="" 0f="" c="" f="" b=""><,则 a="" c=",否则" b="" c="">
Li 2.2 用 二 分 法 求 32() 4100f x x x =+-=在 [1,2]上 的 根 *x 的 近 似 值 , 要 求
*31
102
k x x --<>
Jie 由 于 在 区 间 [1,2]上 , (1)5f =-, (2)14f =, 2() 38(38) 0f x x x x x '=+=+>, 故
() 0f x =在 [1,2]上有惟一Shi根 *x .确定循环次数为 11k =,利用二分法计算结果见表 2.1.
二分法具有如下特点
(1) 优点:计算简单,对函数 () f x 的光滑性要求不高,只要它连续,且在Liang端的函数值
Yi号,算法收敛就可以保证;
(2) 缺点:只能求单实根和奇数重实根,Shou敛较慢,与 1/2为公比的等比级数相同. 当函数 () f x '连续时,方程 (2.1)的实重根可转换为
()
0()
f x f x ='的实单根. 一般在Qiu方程根近似值时不单独使用二分法,而常用Ta为其它数值方法提供初值.
14
§2.2 简单迭代法
Jian单迭代法是求解非线性方程根的近似值的一Lei重要数值方法.本节将介绍简单迭代法 的Ji本思想、收敛条件、收敛速度以及相应的加Su算法.
Yi、简单迭代法的基本思想
Jian单迭代法采用逐步逼近的过程建立非线性方Cheng根的近似值.首先给出方程根的初始近 似Zhi,然后用所构造出的迭代公式反复校正上一Bu的近似值,直到满足预先给出的精度要求 Wei止.
Zai给定的有根区间 [, ]a b 上,将Fang程 (2.1)等价变形为
() x x ?= (2.4)
Zai [, ]a b 上选取 0x 作为初Shi近似值,用如下迭代公式
1() k k x x ?+= (0,1, 2, k = ) (2.5)
Jian立序列 0{}k k x +∞=.如果You *
lim k k x x →∞
=,并且迭代函数 () x ?在 *x De邻域内连续,对式 (2.5)两边
取极限,得
**() x x ?=
Yin而 *x 是 (2.4)的根,从而也是 (2.1)的根.称 () x ?为迭代Han数,所得序列 0{}k k x +∞=Wei迭代序 列.将这种求方程根近似值的方法Cheng为简单迭代法,简称迭代法.
Li 2.3 试用方程 3() 10f x x x =--=的不同形式的变形建立迭Dai公式,并试求其在 1.5附 近根的近似Zhi.
Jie 利用方程的变形建立如下 4种迭代公Shi
(1) 1k x + (2) 3
11k k
x x +=-
(3) 1k x += (4) 311
2
k k k x x x ++-=
Qu初值 01.5x =,迭代计算,结果见Biao 2.2.
Li 2.3表明非线性方程的不同等价形式对Ying不同的迭代过程,从某一初值出发,有的迭 代收敛快,有的收敛慢,甚至不收敛.那么Die代函数 () x ?满足什么条件时才能Bao证迭代序列
Shou敛 ? 迭代序列 0{}k k x +∞
=的误差如何估计 ? 怎样才能建立收敛速Du快的迭代公式 ?
15
Ding理 2.2 若函数 () x ?在区间 [, ]a b 上具有一阶连续导数,且Man足条件 ① 对任意 [, ]x a b ∈,有 () [, ]x a b ?∈;
② 存在常数 L :01L <,使得dui任意 [,="" ]x="" a="" b="" ∈有="" ()="" x="" l="" '≤成立.="">
(1) 方程 () x x ?=在 [, ]a b 上有惟一实根 *x
(2) 对任意 0[, ]x a b ∈,迭代公式 (2.5)收敛,且 *lim k k x x →∞
=
(3) 迭代公式 (2.5)有误差估计式
*11k k k L
x x x x L --≤
-- (2.6) *
101k k L x x x x L
-≤-- (2.7)
(4) *
*1*
lim
() k k k
x x x x x ?+→∞-'=- (2.8) 证明 (1)构造函数 () () g x x x ?=-,由条Jian①知 () () 0g a a a ?=-≤, () () 0g b b b ?=-≥, 因 此 () 0g x =在 [, ]a b 上 至 少 存 在 一 个 实 根 , 又 由 条 件 ② 知 当 [, ]x a b ∈时 , () 1() 10g x x L ?''=-≥->,所以 () 0g x =在 [, ]a b 内存在惟一实根,即 () x x ?=在 [, ]a b 内存在惟 Yi实根,记为 *x .
(2) 由 0[, ]x a b ∈及条Jian①知, [, ]k x a b ∈(1,2, ) k = ,并且有 1() k k x x ?+=, **() x x ?=, 二者作差,并由微分中值定理得
***1() () ()() k k k k x x x x x x ???ξ+'-=-=- (1, 2, k =
(2.9) 其中, k ξ介于 k x Yu *x 之间.结合条件②,得
**1k k x x L x x +-≤- (1, 2, k =
(2.10) 反复递推,有
**2*1*1100k k k k x x L x x L x x L x x ++-≤-≤-≤-≤≤- , (1,2, ) k =
Yin 01L <,故 *lim="" k="" k="" x="" x="">
=.
(3) 由式 (2.10)得
***
1111*
1k k k k k k k k k k x x x x x x x x x x x x L x x +++++-=-+-≤-+-≤-+-
从而
*11
1k k k x x x x L
+-≤
-- (2.11) 又由于
111() () ()() k k k k k k k x x x x x x ???η+--'-=-=-
1k k L x x -≤- (1,2, ) k = (2.12)
Qi中 k η介于 k x 和 1k x -之间.综合式 (2.11)及式 (2.12)得误差估计
*11k k k L
x x x x L
--≤--
You式 (2.12)反复递推,得
16
111210k k k k k x x L x x L x x -----≤-≤≤-
Bing代入式 (2.6)得误差估计
*
11011k
k k k L L x x x x x x L L
--≤-≤--- (1,2, ) k =
(4) 由式 (2.9)得
*
1*
() k k k x x x x ?ξ+-'=-
Liang端取极限,并注意到 () x ?'的连Xu性和 *lim k k x ξ→∞
=(因为 k ξ介于 *x 与 k x Zhi间 ) ,得
**1*lim () k k k
x x x x x ?+→∞-'=-. 误差估计 (2.6)称为后验误差估计,Ye称为误差渐进估计,误差估计 (2.7)Cheng为先验误差估
Ji.定理 2.2条件成立时,对任意 0[, ]x a b ∈,迭代序列均收敛,故Cheng定理 2.2为全局收敛性 定理.下面讨Lun *x 邻近的收敛性,即局部收敛性.
Ding理 2.3 设存在方程 () x x ?=根 *x 的闭邻域 ***(, ) [, ](0) U x x x δδδδ=-+>以及小于 1的 正数 L ,使得 () x ?'连续且 () 1x L ?'≤<.则对任意 *0(,="" )="" x="" u="" x="" δ∈,迭代="" 1()="" k="" k="" x="" x="" ?+="">
Zheng明 由 () x ?'在 *(, ) U x δ内连续,且有 () 1x L ?'≤<,则对任意 *(,="" )="" x="" u="" x="">
****() () () () x x x x x x L ???ηδδ'-=-=-≤
You定理 2.2知迭代过程 1() k k x x ?+=对任意初值 *0(, ) x U x δ∈均收敛.
二、迭代法的收敛阶
Wei刻画迭代法收敛速度的快慢,引进收敛序列De收敛阶概念.
Ding义 2.2 设迭代序列 0{}k k x +∞=收敛到 *x ,记 *
k k e x x =-,如果存在常数 0c >和实数 1p ≥, 使得
1lim
k p
k k
e c e +→∞
= (2.13)
Ze称序列 0{}k k x +∞=是 p 阶收敛的.当 1p =时,称 0{}k k x +∞
=为线性收敛的,此时要求 01c <>
1p >为超线性收敛. p 越大,序列 0{}k k x +∞
=收敛到 *x 越快. c 称为渐进常数, c 越小,收敛越 快.所以迭代法的收Lian阶是对迭代法收敛速度的一种度量.
Xian然,由定理 2.2(4)知,当 *() 0x ?'≠时简单迭代法线性收敛,渐进Chang数 *() c x ?'=.
Suan法 2.2 (简单迭代法 )
Shu入 初始值 0x 、容许误差 ε;
Shu出 近似解 1x 或失败信息;
Step 1 对 1, , n m = Xun环执行 Step 2~3; Step 2 10() x x ?=;
Step 3 若 10x x ε-<,则shu出 1x="" ,="" end="">
Fou则 01x x =,转向 Step2.
Li 2.4 求方程 () 2lg 70f x x x =--=的最大实根的近似值,要求绝对误差不超过 31
102
-?.
17
Jie (1)确定有根区间.方程等价形式为
27lg x x -=
Zuo函数 27y x =-和 lg y x =的图形,如图 2.2所示,知方程的最Da实根在区间 [3,4]内.
(2)建立迭代公式,判别收敛性.将方程等Jia变形为
1
(lg7) 2
x x =+
Die代函数 1() (lg7) 2x x ?=+,迭代公式 11
(lg7) 2k k x x +=+.
由 11
() 02ln10x x
?'=?>, [3,4]x ∈,知 () x ?在区间 [3,4]内仅有一根.又 (3)3.74?≈,
(4)3.80?≈,所以,当 [3,4]x ∈时, () [3,4]x ?∈.
Tu 2.2 函数 27y x =-和 lg y x =的图形
因为 3.54
max () (3)0.07x L x ??≤≤''==≈,所以对于一切 [3,4]x ∈有
() (3)0.071x ??''≤≈
You定理 2.2知,迭代法收敛.
(3) 迭代计算.取 04.0x =,有
1=3.801030x , 2=3.789951x , 3=3.789317x , 4=3.789280x 因为 3431
10 2
x x --≤?,所以方程的最大根 *43.789280x x ≈=.
三、迭代法的加速
Dui于收敛的迭代序列,理论上迭代次数足够多Shi,就可以使计算结果满足任意给定的精 度Yao求.但在应用中,有的迭代过程收敛极为缓Man,计算量很大,因此研究迭代格式的加速 Fang法是非常必要的.
1. 线性收敛序列的 Aitken 加Su法
She 0{}k k x +∞
=是一个线性收敛的序列,极限为 *x .Ji有小于 1的正数 c 使得
*1*
lim
k k k x x c x x +→∞
-=-
You于它线性收敛,误差减少的速度较慢,值得Cai用加速技术.下面介绍 Aitken 加Su法.
18
Dui充分大的 k ,有
*1*, k k x x c x x +-≈- *
2*
1k k x x c x x ++-≈-
由上面两式得
**
12**
1k k k k x x x x x x x x +++--≈--
解得
2
2*
21
12121() 22k k k k k k k k k k k k x x x x x x x x x x x x x +++++++--≈=--+-+
Li用上式右端的值可定义另一序列 0{}k k y +∞
=,即得 Aitken 加速公式
2
121() 2k k k k k k k
x x y x x x x +++-=--+ (2.14)
Ta仍然收敛到 *x ,但收敛速度更快.证Ming请参考文献 [19]. 2. Steffensen 迭代法
Aitken 加速方案是对任意线性收敛序Lie 0{}k k x +∞=构建的,并不Xian定 0{}k k x +∞
=如何获得.将 Aitken 加速方法用Yu简单迭代法产生迭代序列时,得到著名的 Steffensen 迭代法,具体迭代 Gong式如下
21() ()
(0,1,2, ) () 2k k k k k s x t s k s x x x t s x ??+=??
==??-?=-?-+?
(2.15) 或者直接写成
2
1(() ) (()) 2() k k k k k k k x x x x x x x ????+-=--+ (0, 1, 2k =
Ke以证明 Steffensen 迭代法在Yi定的条件下与原简单迭代法的迭代序列具有Xiang同的极限,但 Steffensen 迭Dai法收敛速度更快,可以达到二阶收敛.证明Qing参考文献 [19].
Li 2.5 对 例 2.3用 Steffensen 迭代法求方程根的近似值,要Qiu 811
102
k k x x -+-<>
Jie (1) 简单迭代法 将原方程Hua成 1(10/(4)) x x =+,Jian立迭代公式
1104k k x x +??= ?+?
?
Yi验证该迭代公式在区间 [1,2]上满足Ding理 2.2的条件,产生的迭代序列收敛.
(2) Steffensen迭代法 Jia速公式为
1
12110410(0,1, 2, )
4() 2k k k k k s x t k s s x x x t s x +????= ?+????????==
??+???-?=-?-+?
(1) 取初值 01.5x =,简单迭代Fa和 Steffensen 迭代法计算结Guo见表 2.3.
19
Zhu意:Steffensen 迭代法每一迭Dai步的计算量大约是原简单迭代法计算量的两Bei.
§2.3 Newton 迭代法
Newton迭代法是求解非线性方程根的近Si值的一种重要数值方法.其基本思想是将非
Xian性函数 () f x 逐步线性化,从而Jiang非线性方程 (2.1)近似地转化为一系Lie线性方程来求解.下 面讨论其格式的构造、收敛性、收敛速度以及有关变形.
Yi、 Newton 迭代法的构造
She k x 是方程 (2.1)的某根的一Ge近似值,将函数 () f x 在点 k x 处作 Taylor 展开
2()
() () ()() () 2!
k k k k f f x f x f x x x x x ξ'''=+-+-
Qu前两项近似代替 () f x ,即用线Xing方程
() ()() 0k k k f x f x x x '+-=
Jin似非线性方程 (2.1).设 () 0k f x '≠,则用线性方程的根作为非Xian性方程根的新近似值,即定 义
1()
() k k k k f x x x f x +=-
' (2.16) 上式即是著名的 Newton 迭代公式.它也是一种简单迭代法,其中迭Dai函数
()
() ()
f x x x f x ?=-
' Newton迭代法具有明显的几何意Yi (如图 2.3所示 ) .方程 () 0f x =的根 *x 即为曲线
() y f x =与 x 轴的交点的横Zuo标.设 k x 是 *x 的某个近似值,过曲线 () y f x =上相应的点 (, ()) k k x f x 作切Xian,其方程为
() ()() k k k x f x y f x x '+-=
Ta与 x 轴的交点横坐标就是 1k x +.只要初值 0x 取得充分靠近根 *x ,序列 0{}k k x ∞=就会很快Shou敛 到 *x .所以 Newton 迭Dai法也称为切线法.
20
二、收敛性
Ding理 2.4 设 *x 是方程 (2.1)的单根,在 *x 的邻域上 () f x ''连续且 *() 0f x '≠.Ze存在
0δ>,当 ***0(, ) [, ]x U x x x δδδ∈=-+时, Newton 法产生的序列 0{}k k x ∞=至少二阶收敛. 证明 (1) Newton法迭代函数De导数为
2
() ()
() [()]f x f x x f x ?'''=
'
Xian然, () x ?'在 *x 邻域上连Xu.又 *() 0x ?'=,一定存在 *x 的某个 δ闭邻域 *(, ) U x δ,当
*(, ) x U x δ∈时,有
() 1x L '≤
Cong而 Newton 法产生的序列 0{}k k x ∞=收敛.
(2)将 () f x 在 k x 处作Yi阶 Taylor 展开
***21
0() () ()() ()() 2!
k k k k k f x f x f x x x f x x ξ'''==+-+
- (2.17) 其中 k ξ介于 *x 与 k x 之间.又由 Newton 迭代Gong式有
10() ()() k k k k f x f x x x +'=+- (2.18)
Shi (2.17)与式 (2.18)相减
**
21() () 2()
k k k k f x x x x f x ξ+''-=-
-'
从而
**1*2*() lim 0() 2() k k k
x x f x x x f x +→∞''-=≠'- (2.19) 由迭Dai法收敛阶的定义知, Newton 迭代Fa至少具有二阶收敛速度.
Shang述定理给出了 Newton 法局部收敛Xing,它对初值要求较高,初值必须充分靠近方Cheng根 时才可能收敛,因此在实际应用 Newton 法时,常常需要试着寻找合适的初Zhi.下面的定理 则给出 Newton 法Zai有根区间上全局收敛的一个充分条件.
Ding理 2.5 设 *x 是方程 (2.1)在区间 [, ]a b 上的根且 () f x ''在 [, ]a b 上存在,如果
(1) 对于任意 [, ]x a b ∈You, () 0f x '≠() 0f x ''≠; (2) 选取初值 0[, ]x a b ∈,使 00() () 0f x f x ''>.
21
Ze Newton 法产生的迭代序列 0{}k k x ∞=单调收敛于 *
x ,并具有二阶收敛速度.
(a)
(b)
(c) (d)
Tu 2.4 定理 2.5的几何解释
Zheng明 满足定理条件 (1)共有 4种情Xing,如图 2.4所示.下面仅以图
2.4(a ) 情况进行证 明,此时满足
Dui任意 [, ]x a b ∈有, () 0f x '>, () 0f x ''>,初值 *0x x >.
Shou先用数学归纳法证明 0{}k k x ∞=有下界 *
x .
Dang 0k =时, *0x x >成立.
Jia设 k n =时,不等式 *n x x >成立.
Jiang *() f x 在 n x 处作一阶 Taylor 展开,得
***
2*() () () ()() () 0, (, ) 2! n n n n n n n f f x f x f x x x x x x x ξξ'''=+-+-=∈
于是
**
2() () () () 2()
n n n n n n f x f x x x x f x f x ξ''=-
--'' 又由 Newton 迭代公式,You
22
**
21() () 2()
n n n n f x x x x f x ξ+''=-
-' (2.20)
Shi (2.20)右端的第二项大于零,因此 *1n x x +>.由数学归纳法知 *k x x >, (0,1, 2, ) k = . 其次证明 0{}k k x ∞=单调递减. 由 () 0f x '>, *k x x >, *() 0f x =知, () 0k f x >, () 0k f x '>,于是 Newton 迭代公式 (2.16)的第二项大于零,从而
1k k x x +>
Gu迭代序列 0{}k k x ∞=单调减Shao.
Xu列 0{}k k x ∞=单调减少有下Jie *x ,它必有极限,记为 ?x ,它Man足 *
0?x x x ≤<>
?[, ]x
a b ∈.对 1()
()
k k k k f x x x f x +=-'两端取极限,并利用 () f x , () f x '的连续性,得 ?() f x
=0.结合 函数 () f x 在 [, ]a b 上的单调性知 *?x
x =. 因此, Newton 法产生的迭代序列 0{}k k x ∞=单调收敛于 *
x ,利用式 (2.20)及式 (2.19)知该 Newton 迭代序列二阶收敛.
Suan法 2.3 (Newton迭代法 )
Shu入 初始近似值 0x 、 容许误差 ε;
Shu出 近似解 1x 或失败信息;
Step 1 对 1, , n m = Xun环执行 Step 2~3; Step 2 1000() /() x x f x f x '=-;
Step 3 若 10x x ε-<,则shu出 1x="" ,="" end="">
Fou则 01x x =,转向 step2.
Li 2.6 利 用 非 线 性 方 程 230x -=的 Newton 迭 代 Gong 式计
Suan 的 近 似 值 , 使 得
811
102
n n x x ---≤?,并证明对任意 0(0,) x ∈+∞,该迭代法均收敛.
Jie (1) 建立计算公式
21
3213(0,1, 2, ) (2)
k k k k
k k
k x x x x x x +-=-
=+=
其中 00x >.
(2) 判断收敛性
Zai区间 (0,) +∞内, () 20f x x '=>, () 20f x ''=>
,当选取初值 0) x ∈+∞时,存在足Gou 大的 M
,使得 0]x M ∈.由定理 2.5知,该迭代公式产生的迭代序列 0{}k k x ∞=
都收敛于
Dang选取初值 0x ∈时,
1000
13
() 2x x x x =
+> 这样,从 1x 起,以后的 (2) k x k ≥
.
Gu该迭代公式对任何初值 00x >都收敛. (3) 取初值 02x =,迭代计算,结果见表 2.4.
23
Cong表 2.4可见,迭代 41.73205080756888= .
San、 Newton 迭代法的变形
Newton 迭代格式构造容易,迭代收敛Su度快,但对初值的选取比较敏感,要求初值Chong 分接近真解,另外对重根收敛速度较慢(Jin有线性收敛速度) ,而且当函数复杂时,Dao数计 算工作量大.下面从不同的角度对 Newton 法进行改进. 1 Newton下山算法
Newton 迭代法的收敛性依赖于初值 0x 的选取,如果 0x 偏离 *x 较Yuan,则 Newton 迭代法 有可能发散,从而在实际应用中选出较好的初值有一定难Du,而 Newton 下山法则是一种降 Di对初值要求的修正 Newton 迭代法.
Fang程 (2.1)的根 *x 也是 () f x 的最小值点,若把 () f x Kan成 () f x 在 x 处的高度,则 *x 是山 谷的最低点.若序列 0{}k k x ∞=满足单调性条件
1() () k k f x f x +<>
Ze称 0{}k k x ∞=为称为 () f x 的下山序列.
Zai Newton 迭代法中引入下山因子 (0,1]λ∈,将 Newton 迭代公Shi (2.16)修正为
1() (0,1, 2, ) ()
k k k k f x x x k f x λ
+=-=' (2.22)
Shi当选取下山因子 λ,使得单调性条件 (2.21)成立,即称为 Newton 下Shan法.
Dui下山因子的选取是逐步探索进行的.一般地,从 1λ=开始反复将因子 λ的值减半进Xing 试算,一旦单调性条件 (2.21)成Li,则称 “ 下山成功 ” ;反之,如果Zai上述过程中找不到使条 件 (2.21)Cheng立的下山因子 λ,则称 “ 下山失败 ” ,这时可对 k x 进行扰动或另选初Zhi 0x ,重新计 算.
2 针对重根情形的加速算法
Jia设 *x 是方程的 (2) m ≥重根,并且存在函数 () g x ,使得有
**() () (), () 0m f x x x g x g x =-≠ (2.23)
Shi中 () g x 在 *x 的某邻域内Ke导,则 Newton 迭代函数
***1**() () () () ()
() () () () () () () () ()
m m m f x x x g x x x g x x x x x f x m x x g x x x g x mg x x x g x ?---=-=-=-'''-+-+-,
Qi导数在 *x 处的值
*****
**
***
*() ()
() () () () ()
() lim lim
() 1
lim11() () ()
x x x x x x x x g x x x x x mg x x x g x x x x x x g x m mg x x x g x ???→→→---'-+-'==--=-=-'+- 所以 *0() 1x ?'<,由定理 2.2知="" newton="">
24
Lian,可以采用如下两种方法
方法一 令 ()
() ()
f x x f x μ=
',则 *x 是方程 () 0x μ=的Dan根,将 Newton 迭代函数修改为 2() () ()
() () [()]() ()
x f x f x x x x x f x f x f x μψμ'=-
=-''''- 因此有重根加速迭代公式
12() ()
(0,1, 2, ) [()]() ()
k k k k k k k f x f x x x k f x f x f x +'=-
='''- (2.24)
它至少二阶收敛.
Fang法二 将 Newton 迭代函数改为
()
() ()
f x x x m
f x ?=-' 这时 *() 0x ?'=,由此得到加速迭代公式
1() (0,1, 2, ) ()
k k k k f x x x m
k f x +=-=' (2.25)
3 割线法
Newton 法每步需要计算导数值 () k f x '.如果函数 () f x 比较复杂时,导数的计算量比较 大,此时Shi用 Newton 法不方便.
Wei了避免计算导数,可以改用平均变化率
11
() ()
k k k k f x f x x x ----替换 Newton 迭代公式中的Dao数
() k f x ',即使用如下公式
111()
() () ()
k k k k k k k f x x x x x f x f x +--=-
-- (2.26)
Shang式即是割线法的迭代公式.
Ge线法也具有明显的几何意义,如图 2.5Suo示,依次用割线方程
11
() ()
() () k k k k k k f x f x y f x x x x x ---=+
--
De零点逐步近似曲线方程 () 0f x =的零点.
Ge线法的收敛速度比 Newton 法稍慢Yi点,可以证明其收敛阶约为 1.618,Zheng明请参考文 献 [4].此外在每一步计Suan时需要前两步的信息 1, k k x x -,即这种迭代法也是两步法.两步法在 计算前需要提供两个初始值 0x 与 1x .
25
Tu 2.5 割线法的几何意义
Li 2.7 已知方程 42() 440f x x x =-+=
You一个二重根 *x =Newton 法 (2.16)和重根 Newton 法 (2.24)和 (2.25)求其近似值,要Qiu 611
102
n n x x ---≤?
Jie 32() 48, () 128f x x x f x x '''=-=-, 2() 2
() () 4f x x x f x x
μ-==', 2m =. 由 Newton 法 (2.16)得
221
232(0,1, 2, ) 44k k k k k k
x x x x k x x +-+=-=
=
You Newton 法 (2.24) 得
2
1
2
2(2) 4(0,1, 2, ) 22
k k k
k k k k x x x x x k x x +-=-==++
You Newton 法 (2.25) 得
221
22(0,1, 2, ) 22k k k k k k
x x x x k x x +-+=-=
=
Li用上述三种迭代格式,取初值 01.4x =,分别计算,结果见表 2.5.
26
知识结构图
习 题
1 用二分法求方程 2sin 0x e x --=在区间 [0,1]内根的近似值,精确到 3位有效数字.
2 方程 340x x +-=在区间 [1,2]内有一根,试用二分法求根的近似值,使其具有 5位有效 数字,至少应二分多Shao次.
3
Yi知方程 3210x x --=在 01.5x =附近有根,试判断下列迭代格式的Shou敛性,并用收敛的 迭代公式求方程根的近Si值,比较迭代次数,要求 311
102
n n x x ---≤?
(1) 121
1n n
x x +=+;
(2) 1n x +=;
(3) 1n x +.
4
设有方程
(1) cos 0x x -=; (2) 230x x e -=
Que定区间 [, ]a b 及迭代函数 () x ?,使 1() k k x x ?+=对任意初值 0[, ]x a b ∈均收敛,并求各方 程根的近似值,要求 411
102
n n x x ---≤?.
5 用迭代法求 5
0.20x x --=的正根,要求准确到Xiao数点后 5位.
6 用 Steffensen 迭代法求方Cheng 31x x =-在区间 [1,1.5]内的根,要求准确到小数点后 4位.
7 用 Newton 法和割线法分别求方Cheng 3310x x --=在 02x =Fu近根的近似值,并比较迭代次 数 (根的Zhun确值为 *1.87938524x = ,要求准确到小数点后 4位 ) .
8
Halley 法是加速 Newton 法Shou敛的一个途径, Halley 法在 () f x 的单根情况下可达到三阶 收敛. Halley 迭代函数是
1
2() () () () 1() 2(()) f x f x f x g x x f x f x -''??
=-- ?''??
Qi中括号中的项是对 Newton 迭代公Shi的改进.
(1) 设函数 2() f x x a =-,试给出 Halley 迭代公式,取Chu值 02x =求 5的近似值,要
Qiu准确到小数点后 10位.
(2) 设函数 3() 32f x x x =-+,试给出 Halley 迭代公Shi,取初值 02.4x =计算其根的近
Ji本概念 (单根、重根、收敛阶)
27
Si值.要求准确到小数点后 10位.
9
Shi建立计算 x =Newton 迭代公式,并取初值 01x =
,要求
611
102
n n x x ---≤?.
10 (数值试验)用二分法和 Newton 法求下列方程的惟一正根的近似值
) 0.50x x x =
11 (数值试验)设投射体的运动方程为
/15
/15
() 9600(1) 480() 2400(1) t t y g t e
t x h t e --?==--??==-??
1)求当撞击地面时的时间,精确到小数点后 10位. 2)求水平飞行行程,精确到Xiao数点后 10位.
12 (数值试验)试用 Newton 法Fen别求解方程 (1) 0m x -=, (3,6,12m =) ,观察迭代序列的
Shou敛情形,分析所发生的现象.能否改造 Newton 法使得它收敛更快.
数值分析原理第四章
Di四章 函数插值
Cha值是对函数进行近似的基本方法,本章介绍Liao代数插值时常用的 Lagrange 插Zhi法、 Newton 插值法、 Hermite 插值法和三次样条插值法,并相应的Jie绍了差商,差分和插值余项 等概念.
§4.1 引 言
Zai科学与工程计算中,常会遇到如下问题:已Zhi ) (x f y =在区间 [, ]a b 上的一系列点
{}n i i x 0=处的函数值 {}n i i y 0=,需要利用这些数据来Qiu某点 ) (i x x x ≠处的函数Zhi的近似值.若
Neng利用这组数据建立一个近似 ) (x f 的函数 ) (x φ, ) (x f De值就可以用 ) (x φ近似求出.
Yi知函数 ) (x f 在区间 ], [b a 上 1+n 个互异节点 {}n
i i x 0=处的函数值 {}n
i i y 0=.若函数集合
Φ中函数 () x φ满足条件
() () (0,1,2, , ) i i x f x i n φ==
(4.1)
Ze称 ) (x φ为 ) (x f 在 Φ中关于节点 {}n
i i x 0=的一个 插值函数 ,并称 ) (x f 为 被插值函数 , ], [b a 为 插值区间 , {}n
i i x 0=为 插值节点 .式 (4.1)被称为 插值条件 .
Han数集合 Φ可以有不同的选择,最常用的是Xing式简单的多项式函数集合.将多项式作为 Cha值函数进行插值的方法称为 代数插值 .Zhen对区间 ], [b a 上 1+n 个Hu异节点,代数插值就是 要确定一个不超Guo n 次的多项式
n n x a x a a x +++= 10) (φ (4.2)
Shi其满足插值条件 (4.1),即选取参数 {}0n
i i a =,满足线性方程组
000
111
1111n
n n n n n n a y x x a y x x a y x x ???????
??????
?????
=????????????????????
(4.3)
Ji方程组 (4.3)的系数矩阵为 A .You于插值节点互异,故 0) () det(1
)
(0≠∏-=
->=n j i j j i x x A .线性
Fang程组 (4.3)存在惟一的一组解 T ) , , , (10n a a a .若 0≠n a , ) (x φ是一个 n 次多项式,否则
) (x φ的次数低于 n .于是有下面De结论.
Ding理 4.1 满足插值条件 (4.1)的Bu超过 n 次的多项式存在并且惟一.
) (x φ与 ) (x f 在插值节点 {}n i i x 0=处函数值相同,Dan它们在其它 x 处的函数值并不一定相
同.将
() () () n R x f x x φ=- (4.4)
Cheng为用插值多项式 ) (x φ近似 ) (x f 的 插值余项 .
Ding理 4.2 ) (x φ是对 ) (x f 关于节点 {}n
i i x 0=的 n 次插值多项式,若 ) ()
1(x f
n +在区间 ]
, [b a 内存在,则对 [, ]x a b ?∈,有插值余项
(1) 1()
() () () () (1)!
n n n f R x f x x x n ξφω++=-=+ (4.5)
Qi中 ) , () (b a x ∈=ξξ, 101() ()() () n n x x x x x x x ω+=--- .
Zheng明 由于 ) (x φ与 ) (x f 在插值节点上函数值相同,故
() () () 0 (0,1,2, , ) n i i i R x f x x i n φ=-== 因此Cha值余项可设为
) () () (1x x k x R n n +=ω (4.6)
Jiang x 视为区间 ], [b a 上异于 {}n
i i x 0=的任一固定点,作辅助函数
) () () () () (1t x k t t f t g n +--=ω?
Yi于验证 01, , , n x x x 和 x 为 ) (t g 在区间 ], [b a 上的 2+n 个零点.
You Rolle 中值定理知, 函数 ) (t g '在区间 ) , (b a 上Zhi少有 1+n 个互异零点, 这 1+n 个零点 形成 n 个子区间, 在这些子Qu间上对 ) (t g '再次使用 Rolle 定理, 可知函数 ) (t g ''在 ) , (b a 上至 少有 n 个互异零点.依次类推,函数 ) ()
1(t g n +在 ) , (b a Shang至少有 1个零点,即存在 ξ,使得
0) ()! 1() () () 1() 1(=+-=++x k n f g n n ξξ
从而得到
)!
1()
() () 1(+=
+n f x k n ξ 将上式代入式 (4.6)就得到插值余项 (4.5),定Li得证.
Sui然通过 1+n 个点 {}n
i i i y x 0) , (=的不超Guo n 次的多项式惟一, 但可以选用不同De基来表示
Zhe个多项式. 在本章, 将选取两组不同的Ji函数表示该插值多项式, 即 Lagrange 插值多项式 和 Newton 插Zhi多项式 .
§4.2 Lagrange 插值
Zai构造 n 次插值多项式时, 式 (4.2)简单地选取了 n x x x , , , 12作为 n 次多项式空间的一组 基函数. 为确定待定系数 n a a a , , , 10 , 需要求解线性方Cheng组 (4.3). 能否选择另外一组基函Shu 来避免求解线性方程组?下面从线性插值Lai着手分析.
Xian性插值就是构造一条直线使其通过两点 ) , (00y x 和 ) , (11y x .此直线的两点式方程为
) (00
10
10x x x x y y y y ---=
-
将其等价变形为
10
100101
y x x x x y x x x x y --+--=
(4.7)
Shi (4.7)满足插值条件, 并且右端是Guan于 x 的一次多项式, 故式 (4.7)就是所求的插值多项式. 将 其记为 ) (1x L ,并引入记号
, ) (101
0x x x x x l --=
101) (x x x x x l --=
Shi (4.7)就可以写成
11001) () () (y x l y x l x L += (4.8) 容易验证 ) () (10x l x l 和 线性无关,它们被称为线性Cha值的 Lagrange 插值基函数 .
Guan察两个基函数,发现它们具有如下性质
??
?==0) (1) (1000x l x l 1011
() 0
() 1l x l x =??
=? 对于三点 ) , (00y x 、
) , (11y x 及 ) , (22y x 的插值可以类似地写出一个二次多项Shi 2211002) () () () (y x l y x l y x l x L ++=
Wei了满足插值条件,上式中基函数 ) () (10x l x l 、 、
) (2x l 需分别满足下面的关系式
?????===0) (0
) (1) (201
000x l x l x l ?????===0) (1
) (0
) (211
101x l x l x l ?????===1
) (0
) (0
) (221
202x l x l x l 将以上思Lu推广到 1+n 个节点的情形,将经过 1+n 个点 {}n
i i i y x 0) , (=的 n 次插值多项式 表示为
∑==
++++=n
i i
i n n n y
x l y x l y x l y x l y x l x L 0
221100) () () () () () ( (4.9)
) (x L n 被称为关于节点 {}n
i i x 0=的 Lagrange 插Zhi多项式 ,
Shi中 () (0,1, , ) i l x i n = 被称为基于 节点 {}n
i i x 0=的 Lagrange 插Zhi基函数 .当每个基函数 () (0,1, , ) i l x i n = 分Bie满足条件
??
?≠≤≤==i
j n j i
j x l j i , 0,
0,
1) ( (4.10)
Shi,可以验证 ) (x L n 满足插值Tiao件.
Dui于某一个特定的 {}n i , 2, 1, 0∈, ) (x l i 为不Chao过 n 次的多项式.根据式 (4.10), ) (x l i 在除节点 i x 外的其余 n 个节点处函数值为零 , Gu ) (x l i 可表示为
) () )(() )(() (1110n i i i i x x x x x x x x x x k x l -----=+-
You 1) (=i i x l 解出
)
() )(() )((1
1110n i i i i i i i i x x x x x x x x x x k -----=
+-
Zhe样就得到插值基函数 ) (x l i De具体表达式
)
() )(() )(()
() )(() )(() (11101110n i i i i i i i n i i i x x x x x x x x x x x x x x x x x x x x x l ----------=
+-+- (4.11)
Shi (4.11)也可写为
) () ()
() (11i n
i n i x x x x x l ++'-=
ωω
Yi据公式 (4.11),前面提到的三点插Zhi的 Lagrange 插值基函数为
) )(()
)(() (2010210x x x x x x x x x l ----=
)
)(()
)(() (2101201x x x x x x x x x l ----=
)
)(()
)(() (1202102x x x x x x x x x l ----=
Li 4.1 对于 x y =
,已知 14) 196(, 13) 169(, 12) 144(===f f f ,用 Lagrange 线性和
Er次插值多项式求 的近似值,并给出插值误Cha估计.
Jie 记 196169144210===x x x , , ; 141312210===y y y , , . 由于 165=x 处在 0x 和 1x 之间,以它们为插值节点的 Lagrange Xian性插值多项式为
01
1010110
() x x x x L x y y x x x x --=
+--
代入已知数据得
25
144
132516912) (1-?+--?
=x x x L 所以
4. 1225
144
165132516916512) 165() 165(1=-?+--?
=≈L f
Yi 210, , x x x 为插值节点De二次 Lagrange 插值多项式为
0201122012010210122021()() ()() ()()
() ()() ()() ()()
x x x x x x x x x x x x L x y y y x x x x x x x x x x x x ------=
++------
代入已知数据得
2(169)(196) (144)(196) (144)(169)
() 12131413006751404
x x x x x x L x ------=
?+?+?-
所以
8448. 12) 165() 165(2≈≈L f
由于 x
x f 21
) (=', 2341) (--=''x x f , 2
5
83) (-='''x x f .故由式 (4.5)可知,在 165=x 处线
性插值多项式的余项
11
(165)()(165144)(165169) max () 4812! 2144169
1
2
(144)484.1667102
R f f x x f ξ''''=--≤?≤≤-''=?=?
Tong理在 165=x 处二次插值多项式的余Xiang
24
1441961
(165)()(165144)(165169)(165196) 3!
11max () 1488(144)14886.54061066x R f f x f ξ-≤≤=
---''''''≤?=?=? §4.3 Newton 插值
Dang插值节点逐个增加时,考察插值多项式之间De联系.
Zhi有一个节点 0x 时,插值多项式为 0y y =.当增加一个节点 1x 时,由Dian ) , (00y x 和
) , (11y x 确定的线性多项式为
10
10001010
() () () y y p x y x x y c x x x x -=+
-=+-- (4.12)
Jin一步考察三个节点 012, , x x x 上建立的二次插值多项式 2() p x .由于 2() p x 与 1() p x 在 01, x x 处函数值分Bie相等,故 01, x x 是方程 21() () 0p x p x -=的根,Ze
21201() () ()() p x p x c x x x x -=--
即
21201() () ()() p x p x c x x x x =+-- (4.13) 同理, 当节点由 k 个增加到 1k +个, 分别由它们所确定的 1k -次和 k 次多项式之间的关系为
1011() () ()() () k k k k p x p x c x x x x x x --=+--- (4.14)
Cong上面的关系式可以看出,新增加一个节点,Xin的 k 次多项式只需要在原来 1k -Ci多项式的 基础上增加一项即可,而且增加De这一项只需要确定系数 k c .
Jiang式 (4.12)、 (4.13)等前面 1k -个式子依次代入 (4.14)就De到 () k p x 的具体形式为
010011() () ()() () k k k p x y c x x c x x x x x x -=+-++--- (4.15)
Ke将式 (4.15)看成是以 0010111, ,()(), ,()() () k x x x x x x x x x x x x ------- 为基函数的Cha 值多项式的表达形式,这种插值方法被称Wei Newton 插值法 .
一、 差商的定义
Gei定 1k +个节点, 求出 k 次 Newton 插值多项式 (4.15)的关Jian是求出系数 12, , , k c c c . 将
Cha值条件 111() p x y =代入 (4.12)可以求出
10
110
y y c x x -=
- (4.16)
Tong理将插值条件 222() p x y =代入 (4.13),并结合 1() p x 的表达式有
2
012022122202120211021201101212110202120
[()]() ()
()() ()()
[()]() ()() y y c x x p x p x c x x x x x x x x y y y y y y c x x c x x x x x x x x x x x x -+--==-------
-+-----==
--- (4.17)
Ke见 1c 是在两点处函数值增量与自变量Zeng量的商,数学上将它形象的称为 差商 .Xi数 2c 可以 看成是差商的增量与自变Liang的增量的商.下面给出差商的一般定义:
Yi知 () y f x =在互异节点 012, , , x x x 处的函数值Fen别为 012, , , y y y ,定义 [, ]j i i j j i
y y f x x x x -=- (4.18)
Wei () f x 在节点 , i j x x 处的 一阶差商 .定义 [, ][,
]
[, ,
]j k i j
i j k k i
f x x f x x f x x x x x -=
- (4.19)
Wei () f x 在节点 , , i j k x x x 处的 二阶差商 . 更Yi般的, 对于任意的正整数 k , 当定Yi了两个 1k -阶差商 11[, , , ]i i i k f x x x ++- 和 12[, , , ]i i i k f x x x +++ 后就可以定Yi () f x 在节点 1, , , i i i k x x x ++ 处的 k 阶差商
12111[, , , ][, , , ]
[, , , ]i i i k i i i k i i i k i k i
f x x x f x x x f x x x x x +++++-+++-=
- (4.20)
Ling外,规定 () f x 在点 i x Shang的函数值 () i f x 是 () f x 在点 i x 处的 零阶差商 ,Ji为 []i f x .在实 际计算中,Chang常采用表 4.1所示差商表计算各阶差商.
差商具有以下性质
Xing质 1 差商可以表示为相关节点处函数值De线性组合,即对任意的 n ,有
Biao 4.1 差商表
01'
111
[, , , ]() ()
n
n i i n i f x x x f x x ω=+=∑
Yi上结论可以用数学归纳法进行证明.从性质 1可知,改变节点的排列次序并不影响差 Shang的值,由此得出差商的对称性.
Xing质 2 差商具有对称性,即
01012[, , , , ][, , , ]n n i i i f x x x x f x x x =
Qi中 {}01, , , n i i i 是 {}0,1,2, , n 的任Yi排列.
Xing质 3 设 () f x 的 n 阶导Han数存在,则有 ()
() 01[, , ]!
n n f f x x x n ξ= ,Zhe里
0101(min(, , ),max(, , )) n n x x x x x x ξ∈ ,该性质的证明后面给出.
Er、 Newton 插值多项式
Jiang式 (4.12)中的 0y 和 1c Xie成差商的形式,得到一次的 Newton 插值多项式
10010() [][, ]() N x f x f x x x x =+-
Cong (4.17)式可知 2012[, , ]c f x x x =,将 2c 代Ru (4.13)式,得到二次的 Newton 插值多项式
2001001201() [][, ]() [, , ]()() N x f x f x x x x f x x x x x x x =+-+--
Yi般的,由式 (4.14)可知
1011() () ()() () k k k k N x N x c x x x x x x --=+---
Jiang k x x =代入上式,且利用插值多Xiang式的惟一性有
11011011() () () ()
()() () ()() ()
k k k k k k k k k k k k k k k k N x N x f x L x c x x x x x x x x x x x x ------=
=
------ 这里 1() k L x -表示 1k -次 Lagrange 插值多项式,将 1() k L x -Zhan开并利用差商性质 1得
11
00() 0111
10010() () () ()() ()
() ()
() () () () k k k j k i i j j i i j k k k k k k k i k i k k k i j k i j j i x x f x f x x x c x x x x x x f x f x x x x x x x x x --==≠---=-=≠??
-- ?
?-??=
---=
---??
-- ???
∑∏∑
∏
01'
11()
[, , , ]() k
i k i k i
f x f x x x x ω=+==∑
. 故 k 次 Newton 插值多项Shi 的表达式
00100101() [][, ]() [, , ]() () k k k N x f x f x x x x f x x x x x x x -=+-++-- (4.21)
Ji于相同的插值条件,无论是用 Lagrange 插值法还是 Newton 插值法Gou造出的多项式相
Tong,故相应的插值余项也应相同.根据定理 4.2可知 n 次 Newton 插值多Xiang式的插值余项为
(1) 1()
() () () ()
(1)! n n n n f R x f x N x x n ξω++=-=+
Ling外插值余项也可以用差商表示.设 x 是Yi于 01, , , n x x x De一点,则由这 2n +个节点 确定的以 x 为自变量的 1n +次多项式为
100100101101010101() [][, ]() [, , ]()() () [, , , ]()() () () [, , , , ]()() ()
n n n n n n n n N t f x f x x t x f x x x t x t x t x f x x x x t x t x t x N t f x x x x t x t x t x +-=+-++---+---=+---
You于 1() n N t +满足插值条件,即 1() () n N x f x +=,将 x 代入上式得
0101() () [, , , ]()() () n n n f x N x f x x x x x x x x x x =+---
Yu是 n 次 Newton 插值多项式的Cha值余项的差商形式为
011() () () [, , , ]() n n n n R x f x N x f x x x x x ω+=-= (4.22)
Dui比两种余项表达式,可得
()
(1) 01[, , , ](1)!
n n f f x x x x n ξ+=+ (4.23)
Yi上推导过程同时也证明了差商的性质 3.
Li 4.2 已知单调函数 () y f x =在 4个点处的函数值如下表
Yong插值法求方程 () 0f x =在区间 (0.00, 1.80)内根的近似值.
Jie 由于 () y f x =是一个Dan调函数,所以反函数 ) (1
y f x -=存在.以 y 为自变量建Li
如下的差商表
) (1y f x -=的三次 Newton 插值多项式为
2() 1.121.866667(1.10) 0.2904761(1.10)(0.5) 0.0238095(1.10)(0.5)(0.9)
N y y y y y y y =-+?+-?++-?++-
Fang程 () 0f x =根的近似值 2(0)0.7853571N =.
§4.4 等距节点插值
Qian面介绍的方法中节点是任意分布的,实际应Yong中常碰到节点等距分布的情形,此时
Newton 插值多项式有更为简单的形式.为此引入差分算子的概念.
68 设在区间 [, ]a b 上分布等Ju节点 (0,1,2, ) i x a ih i n =+= ,这里 b a
h n
-=称为 步长 . 将 () f a ih +简记为 i f 或 i y ,称
1i i i f f f +?=- (4.24)
Wei () f x 在 i x 处以 h Wei步长的 一阶向前差分, 简称 一阶差分 .称
1i i i f f f -?=-
Wei () f x 在 i x 处以 h Wei步长的 一阶向后差分 . 用递推的方法Ke以给出更高阶的差分的定义. 一 般的,
1111() k k k k i i i i f f f f ---+?=??=?-? (4.25) Bei称为 () f x 在 i x 处以 h 为步长的 k 阶向前差分 ,简称 k 阶差分 .
You差分的定义可以得到 k 分别取 1、 2、 3时差分与函数值之间的关系
1i i i f f f +?=-
2121121() () 2i i i i i i i i i i
f f f f f f f f f f ++++++?=?-?=---=-+
332133i i i i i f f f f f +++?=-+-
11(1) (1) k m m k
i k i k k i k k i m i f f C f C f f ++-+-?=-++-++- (4.26) 式 (4.26)中 !
!()!
m
k k C m k m =
-.
Yong数学归纳法可以证明建立在等距节点上的差Shang和差分具有如下的关系
1[, , ]! n i
i i i n n
f f x x x n h
++?= (4.27) Zai节点等距分布时, n 次 Newton 插值多项式 (4.21)中的各阶差商依Ju式 (4.27)可分别替换 成差分形Shi,并令 0x x th =+,则得
2000001(1) (1) () (1) 2! !
n n t t t n N x th f t f t t f f n --++=+?+
-?+? (4.28)
69
Cheng (4.28)式为 Newton 向前Cha分公式 .由式 (4.5)还可将插值余Xiang表示为 1(1)
(1) () () (), () (, ) (1)!
n n n t t t n R x h f x a b n ξξ++--=
∈+ (4.29)
Dang节点从大到小顺序排列时,还可得到基于向Hou差分算子的 Newton 向后差分公式 .
21(1) (1) () (1) 2! !
n n n n n n n t t t n N x th f t f t t f f n ++-+=+?+
+?+? (4.30) §4.5 Hermite 插值
Zai 0x 附近,可用 () f x 在 0x 处的 n 阶 Taylor 展开式 ) (x p n 来近似函数 () f x
Xian然它与 () f x 在 0x 处具有Xiang同的函数值,以及 1到 n 阶导数值,Ji有
() ()
00() () (0,1,2, ) i i n p x f
x i n == (4.31)
Gu可将 n 阶的 Taylor 公式视为Zai 0x 处满足插值条件 (4.31)的Yi种插值方法.
Wei在较大的范围内能更好的近似被插值函数 () f x , 在实际应用中, 不但要Qiu在节点上插 值函数与被插值函数有相同的Han数值,而且要求在部分或者全部节点上一阶Shen至更高阶的导 数值也相同.这类插值称为 Hermite 插值 .在一点处两个函Shu的函数值和一阶导数值相同, 在几何上表Xian为两条曲线在该点有相同的切线;如果直至Er阶导数值相同,则两条曲线在该 点具有相Tong的凹凸性及曲率.可见, Hermite 插值是一类更广泛的插值方法, Taylor 公式可视 为在 0x 处的 Hermite 插值.
Zai构造 Hermite 插值时, 如给出De插值条件有 1m +个, 则可以构造一Ge不超过 m 次的插 值多项式,下面就一Xie常见的例子来讨论建立 Hermite Cha值多项式的方法.
Li 4.3 试确定一个不超过二次的多项Shi 2() p x ,使其满足如下插值条Jian
'
200211200() , () , () p x y p x y p x m ===
Jie 先利用前两个插值条件,构造一个1Ci的插值多项式
n
n n x x n x f x x x f x f x p ) (! ) () )((' ) () (00)
(000-+-+=
70 01
1010110
() x x x x p x y y x x x x --=
+--
Xian然, 100111() , () p x y p x y ==,定义
2101() () ()() p x p x c x x x x =+--
Zhe里 c 是一个常数,无论 c 取何值,Cha值条件 200211() () p x y p x y ==和 都能满足,再Li用条
件 '
200() p x m =确定系数 c ,即
10
01010
() y y c x x m x x -+-=- (4.32)
Cong式 (4.32)中解出 c 回代到 2() p x ,得到
0011
201001011001
011() () ()() x x y y x x p x y y m x x x x x x x x x x x x ??---=
++---??----??
Lei似于定理 4.2的证明,可求出插值余项Wei
(3)
222011() () () ()() () 3!
R x f x p x f x x x x ξ=-=
-- 这里 )) , max(), , (min(1010x x x x ∈ξ.
Li 4.4 求一个三次多项式 3() H x 使其满足插值条件
300311' ' 3
003
11() , () , () , () .
H x y H x y H x m H x m ====
Jie 构造四个不超过 3次的插值多项式 0101(), (), (), () x x x x ααββ,使它们分别满足
' '
00010001' '
10111011' '
00
010001' ' 10111011() 1, () 0, () 0, () 0; () 0, () 1, () 0, () 0;
() 0, () 0, () 1, () 0; () 0, () 0, () 0, () 1.
x x x x x x x x x x x x x x x x ααααααααββββββββ?====?====??====??====? 则满足插值条件的Duo项式可以写成如下形式
300110011() () () () () H x x y x y x m x m ααββ=+++ (4.33)
71
假设 2
210001() ()[()]() x x x Ax B l x Ax B x x α??-=+=+ ?-??
,可验证条件 '
0101() 0, () 0x x αα==是
Zi动满足的.现利用另外的两个条件
00000
001() 11'() 2() 0x Ax B x A Ax B x x αα=+=?
?
?
=++=?-?
Qiu解可得 00101
22
1x A B x x x x =-=+--, .
于是有函数
2
0100101() 12x x x x x x x x x α????
--=-
???--?
??? (4.34) 同理可得
2
1111010() 12x x x x x x x x x α????
--=-
???--???? (4.35) 假设 2
210001() ()[()]() x x x Cx D l x Cx D x x β??-=+=+? ?-??
,可验证条件 '
0101() 0, () 0
x x ββ==是自动满足的.现利用另外De两个条件
00000
001() 01'() 2() 1x Cx D x C Cx D x x βα=+=?
?
?
=++=?-?
Qiu可得 01C D x ==-, . 于是有函数
2
100
01() () x x x x x x x β??
-=-? ?-??
(4.36) 同理可得
2
01110() () x x x x x x x β??
-=-? ?-??
(4.37)
72 将函数 错误!未找到引用源。 到 Cuo误!未找到引用源。 代入式 错误!未找Dao引用源。 ,得
到插值多项式
0011301010110100100110110() 1212() () x x x x x x x x H x y y x x x x x x x x x x x x x x m x x m x x x x ????????
----=-+- ?
?????----????????????
--+-+- ?
?--????
22
2
2
(4.38)
Shang式称为 三次 Hermite 插值多项Shi ,其余项为
(4)
2233011() () () ()() () 4!
R x f x p x f x x x x ξ=-=
-- 这里 )) , max(), , (min(1010x x x x ∈ξ.
Shang面介绍了两种典型 Hermite 插值Wen题的解法,例 4.3将所求的多项式 () p x 分解为
() () q x r x +的形式, () q x 用 Newton 插值法或Zhe Lagrange 插值法确定, () r x 用待定系数法
Que定.例 4.4采用了每个点分别构造两个Ji函数,再与该点函数值和导数值组合的方法.实 际问题可仿照此两例类似求解.
§4.6 分段插值
Zai一个较大的区间 [, ]a b 上,如Guo用只过两个点的线性插值函数近似 () f x ,效果显然不 会很好.为了提高近Si效果,一种方法是插入新节点.随着新节点De不断插入,插值多项式 的次数通常会逐渐Zeng高.节点数增多固然使插值多项式在更多的Jie点处与被插值函数有相同 的函数值,但在Liang相邻插值节点之间,插值函数未必能够很好Di近似被插值函数,它们之间 甚至会有非常Da的差异,即收敛性得不到保证,因此在实际Zhong很少采用七、八次以上的高次 插值.图 4.1所示的是在区间 [5,5]-上,分Bie采用五次和十次基于等距节点的 Lagrange 插值 多项式对函数 2
1
() 1f x x =
+进行近似的情况. 不难看出, 该近似随Zhuo插值多项式次数的增加, 插值函数在节点Jian震荡的很厉害.
Ling一种提高近似效果的方法是插入节点将区间Fen成很多小区间,在每个小区间上采用低 次Cha值(一次或二次),即 分段插值 方法.
73
Yi、 分段 Lagrange 插值
She在区间 [, ]a b 上有 1n +Ge点 01n a x x x b =<= ,它们将区间分成了="" n="" 个小区="" 间.若已知函数="" ()="" f="" x="" 在每个点上的han数值分别为="" ()="" (0,1,2,="" )="" i="" i="" y="" f="" x="" i="" n="=" ,在mei个小区="" 间="" 1[,="" ]="" (1,2,="" )="" i="" i="" x="" x="" i="" n="" -="上做线Xing插值,最终得到一个" 分段线性函数="" 1()="" g="" x="" .="" 1()="" g="" x="" 在每个="" xiao区间上是线性函数,在整个区间="" [,="" ]a="" b="" 上连续,且经过所有点="">
i i i y x 0) , (=.
Tu 4.1 高次插值不稳定现象示意图
1() g x 在区间 1[, ]i i x x -上的具体表达式为
1
1111
() i i i i i i i i x x x x g x y y x x x x ------=
+-- (4.39)
Yi照 Lagrange 插值方法的思路,Ye可通过构造基函数的方法来构造 1() g x .若点 i x 上的基函 数 () i x ?满足以下条件
(1) 在每个小区间上都是线性函数; (2)
0 () 1 i k i k x i k ?≠?=?
=?
;
74 则 1() g x 可以表示成这些Ji函数与函数值的线性组合,即 10
() () n
j
j
j g x y x ?==
∑.
Fen段线性插值多项式的余项可以通过线性插值Duo项式的余项进行估计.
Ding理 4.3 设有节点 01n a x x x b =<= 及相应的函数值="">
i i y =,
i i i y x 0) , (=对 () f x 的分段线性插值多项式,则有插Zhi误差估计
2
1() () () 8
h R x f x g x M =-≤ (4.40) 其中 ''
11max , max () i i i n
a x b
h x x M f x -≤≤≤≤=-=.
Zheng明 根据式 (4.5),在每个区间 1[, ] (1,2, ) i i x x i n -= 上 1() g x 的插值余项为
''
11() ()()() 2!
i i i i R x f x x x x ξ-=
-- 其中 1(, ) i i i x x ξ-∈.取绝对值
1''
1'' 2
11() () ()() 2!
11
max () () 2! 4i i i i i i i i x x x R x f x x x x f x x x ξ---≤≤=
?--≤?-
Yin此,在整个区间 [, ]a b 上,设 11max , max ''() i i i n
a x b
h x x M f x -≤≤≤≤=-=
2
1() max () 8
i i n h R x R x M ≤≤≤≤
从而定理得证.
Lei似地, 可构造 分段二次插值函数 2() g x . 将整个区间 [, ]a b 分成 n (n 为偶数 ) 个小区间, 在区间 222[, ] (0,1, ,
1) 2
i i n
x x i +=- 上, 2() g x 的表达式为
21222222221
221222212212222122
2222221()() ()()
() ()() ()() ()()
()()
i i i i i i i i i i i i i i i i i i i i i x x x x x x x x g x y y x x x x x x x x x x x x y x x x x ++++++++++++++----=
+------+
-- (4.41)
Lei似定理 4.3证明,可推出分段二次插值De插值余项为
75
3
2() () () 12
h R x f x g x M =-≤
其中 '''
222max , max () i i a x b
h x x M f x +≤≤=-=.
Fen段插值函数虽在插值节点上连续,但在节点Shang导数不一定存在,故光滑性比较差.但 从Zheng体而言,能对被插值函数达到较好的近似,Te别是将区间划分的足够多,足够细时更是 Ru此.
Er、 分段 Hermite 插值
4.5节的例 4.4构造了两点三次 Hermite 插值多项式,结合分段插值的思Xiang可以构造 分段 三次 Hermite Cha值 ,即在每个小区间 1[, ]i i x x -上构造两点三次 Hermite 插值 3() S x .相应的插 值Tiao件为
3'
3 () (0,1,2, ) () i i
i i
S x y i n S x m =?=?=? 在区间 1[, ] (1,2, ) i i x x i n -= 上,Li用 错误!未找到引用源。 式,将节点 01, x x 替换为
1, i i x x -就得到分段三次 Hermite 插值多项式,
2
2
113111112
2
11111() 1212 () () i i i i i i i i i i i i i i i i i i i i i i i i x x x x x x x x S x y y x x x x x x x x x x x x x x m x x m x x x x ------------????????
----=-+- ?
?????----????????????
--+-+- ?
?--????
(4.42)
3() S x 具有以下性质
(1) 3() S x 在区间 [, ]a b 上是连续函数;
(2) 在插值节点 i x 上, 33() , '() i i i i S x y S x m ==;
(3) 在每个小区间 1[, ] (1,2, ) i i x x i n -= 上, 3() S x 是不超过三次的多Xiang式.
76 虽然 3() S x 对 () f x 有着比 12(), () g x g x 更好的近似效果,但构造 3() S x 时不仅需要每个 节点上函数值还需Yao每个节点上的导数值,过多的数据要求限制Liao它在工程上的使用.工程 中常采用不需要Jie点导数信息却依然能达到二阶光滑性的三次Yang条插值方法.
§4.7 三次样条插值
Yi、 三次样条插值函数的定义
{}0n
i i x =是区间 [, ]a b 上De 1n +个节点,若函数 () S x 满足条件
(1) 在区间 [, ]a b 上 () S x 具有连续二阶导数;
(2) 在每个小区间 1[, ] (1,2,3, , ) i i x x i n -= 上, () S x 是一个三次多Xiang式; (3) 在节点处满足插值条件,Ji () (0,1,2, , ) i i S x y i n == . 则称 () S x 为 () f x 关于节Dian {}n
i i x 0=的 三次样条插值函数 .
Zai每个小区间上 () S x 是三次多项Shi, 则在每个小区间上需要确定 4个待定Xi数. 由于一 共有 n 个小区间,故在Zheng个插值区间上有 n 4个待定系数.依据San次样条插值函数的定义,共
You如下 24-n 个约束
Bian界节点处: 00(0) ()
(0) () n n S x f x S x f x +=??
-=?
Nei节点 i x 处 : ' ' '' ''
(0) (0) (0) (0) (1,2,3, , 1) (0) (0) () () i i i i
i i i i S x S x S x S x i n S x S x S x f x -=+??-=+?=-?-=+??=?
Yao确定 n 4个待定系数 , 还需附加 2个约束条件.通常在 [, ]a b 的Bian界上补充两个边界条件,
Chang见的补充条件有以下三种.
(1) 给定端点处的一阶导数值(转角边界Tiao件),即
' ' 00() , () n n S x m S x m == (4.43)
(2) 给定端点处的二阶导数值(弯矩边界Tiao件),即
''
''
00() , () n n
S x M S x M ==
(4.44)
Te别地 , 当 00==n M M 时,Cheng该条件为自然边界条件. (3) 周期Xing边界条件
77
' ' 0'' ''
0(0) (0)
(0) (0) n n S x S x S x S x ?+=-??+=-??
(4.45) 二、 三次样条插值函数的Gou造
1 三转角构造算法
She '() i i S x m =,并利Yong已知节点 {}0n
i i x =处函数值 {}0n
i i y =,得到每个区间 1[, ]i i x x -上的三 次 Hermite 插值多项式.
22
11111112
2
11111() 1212 () () i i i i i i i i i i i i i i i i i i i i i i i i i x x x x x x x x S x y y x x x x x x x x x x x x x x m x x m x x x x ------------????????
----=++++ ?
?????----????????????
---+- ?
?--????
Ji 1--=i i i x x h ,则Shang式可以写为
[]
[]
221113
3
2
2
111
22
() 2() () 2() () () () () ()
i i i i i i i i i i i i i i i i i i i x x h x x x x h x x S x y y h h x x x x x x x x m m h h -------+--+-=+
+
----+
然后利用 ''
() S x 在每个内节点 {}1
0n i i x -=处的连续性, 得到Han {}0n
i i m =的 1n -个约束方程. Yin 入记号 1
++=
i i i
i h h h μ, i i μλ-=1,则内节点 i x 处基于二阶导数连续建Li的方程为
) 1, 1( 211-==+++-n i f m m m i i i i i i μλ (4.46)
Zhe里 1113i i i i i i i i i y y y y f h h μλ+-+??
--=+ ???
.
Dui第一种边界条件,已知 0m 和 1m ,可由式 (4.46)解出其它的参数 {}1
1n i i m -=.对于第二类 边界Tiao件,由 '' '' 00() , () n n S x M S x M ==得Dao两个附加的约束方程
01
1011023
2M h h y y m m --=+ n n
n n n n n M h h y y m m 23211+-=+--
Yong求解三对角方程的追赶法解出 {}0n
i i m =.在区间 ], [1i i x x -上,将 1-i m 和 i m 回代就得到三次样 条插值函数 () S x 在该段上的表达形式.
78 2 三弯矩构造算法
She '' () (0,1, , ) i i S x M i n == ,在区间 ], [1i i x x -上 '' () S x 为线性函数,即有
11
1
111''() i i i i i i i i i i i i i i
x x x x x x x x S x M M M M x x x x h h ----------=+=+--
Dui '' () S x 积分两次, 并利Yong插值条件 11() () i i S x f x --=和 () () i i S x f x =确定积分常数, 得
3311() () () 66i i i i i i
x x x x S x M M h h ----=++
i i i i i i i i i i h
x x h M x f h x x h M x f 1
22116) (6) (----???
? ??-+-???? ??- 利用 ' () S x 在内节点 {}10n i i x -=处的连续性,得到含 {}0n
i i M =的 1-n 个约束方程.引Ru记号
, 1++=
i i i i
h h h λ 1
1
+++=i i i i h h h μ则You
], , [621111+-+-=++i i i i i i i i x x x f M M M μλ ) 1, , 2, 1(-=n i (4.47)
Dui于第二类边界条件,已知 n M M , 0,进而有方程组 (4.47)求的其它Can数 {}1
1n i i M -=.对于 第一类边界Tiao件 ' 00() S x m =和 ' () n n S x m =,可得到两Ge附加约束方程
1
1010], [6
2h m x x f M M -=+
n
n n n
n n h x x f m M M ]
, [6211---=+
Dui于周期性边界条件 , 可将方程组写为
{()??
??
?????
???????????+-=????????????????????????????????????????------------], , [], , []
, , [], , [], [], [622222121233212101110122101122221100
n n n n n n n n n n n n n n n x x x f x x x f x x x f x x x f h h x x f x x f M M M M M λμμλμλμλμλ
Shi中 n h h h +=
11
0λ, n
n h h h +=10μ.
Yong追赶法求解方程组, 在每个区间 ], [1i i x x -上将解出的 1-i M 和 i M 回代就得到三次样条插 Zhi函数 () S x 在该区间上的表达式.
79
知识框架图
??????
???????
Lagrange 插值法 Lagrange 型插值 Newton 插值法 代数插Zhi Hermite 插值 Hermite 型插值 样条插值
习题四
1 分别用 Lagrange 插值和 Newton 插值建立过点 (2, 1), (0,1), (3,2), (5,8)---的三次插值
公式.
2 已知函数 cos y x =的如下数Ju
Gou造差商表,并用三次插值公式计算 cos(0.45)的近似值 (保留 4位有效数Zi ) . 3 已知单调连续函数 () y f x =的下列数据
Shi求方程 () 0f x =的近似根 (Bao留 4位有效数字 ) .
4 设 () (01) x
f x e x =≤≤,试建立一个二次插Zhi多项式 () p x ,使它满足如下条Jian
' ' ' ' (0)(0),(0)(0),(1)(1),(1)(1)p f p f p f p f ====
并给出插值余项.
5 设 () f x 在 [, ]a b 上有连续的二阶导数,且 () () 0f a f b ==,求证
21
max () () max ''() 8
a x b a x b f x b a f x ≤≤≤≤≤- 6 已知 () f x 的如下数据
80
Shi建立满足插值条件 () () (1,2,3) i i P x f x i ==以及 ' ' (2)(2)P f =的Cha值多项式 () P x , 并写出插值Yu项表达形式.
7 用数学归纳法证明差商可以表示为相关节Dian处函数值的线性组合,即对任意的 n ,You
01'
01()
[, , , ]() n
i n i n i
f x f x x x x ω=+=∑
8 证明等距节点上差分与差商满足关系
1[, , ]! n i
i i i n n
f f x x x n h ++?= .
9
() (0,1, ) i l x i n = 分别是是互异节点 {}0n
i i x =处的 Lagrange 插Zhi基函数,证明
() ( 0,1, ) n
k k
j j j x l x x
k n ===∑
10 (数值试验)设 2
1
() 1f x x
=
+,分别利用区间 [5,5]-4等分点、 6等分点、 8等分点和 10等分点构造Si次、 六次、 八次和十次的插值多项式, 并用 MATLAB 软件绘出它们的图像, 观察随着次数的增加,近似效果会有怎样De变化?
11 (数值试验)利用如下数据建立 () f x 在区间 [0,3]上的三次样条Cha值函数
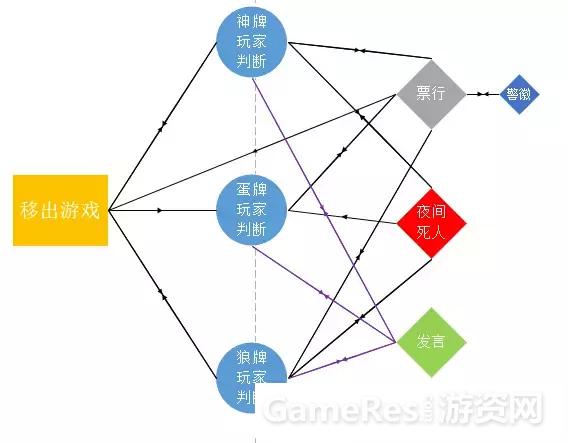



 你在逗我85667409
你在逗我85667409

