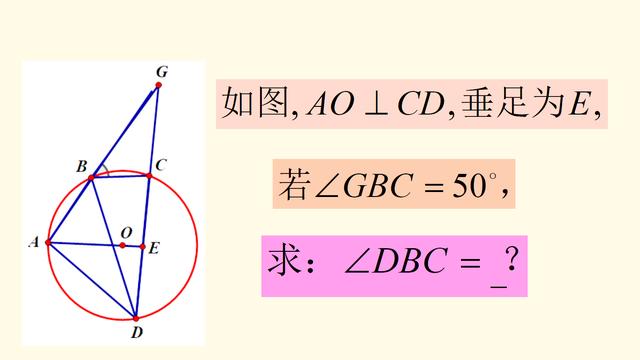
范文一:初三数学考试题
初三数学考试题
一 、选择题 (每一题4分 总共40分)
1、方程 的解为( )
A、无实数解 B、1或2 C、0 D、2 2、方程 化为 形式后,a、b、c的值为( )
(A)1,–2,–15 (B)1,–2,–15(C)1,2,–15 (D)–1,2,–15 3(若半径为7和9的两圆相切,则这两圆的圆心距长一定为( ). (A)16 (B)2 (C)2或16 (D)以上答案都不对
4(若点 A(-5,2m-1)关于原点的对称点在第一象限,则 m的取值为( )
(A) m <1 (b)="" m="">1/2 (C) m =1/2 (D) m ?1/2 5(如图,PA切?O于点A,PO交?O于点B,若PA=6,BP=4,则?O的半径为( )
(A) 5/2 (B) 5/4 (C)2 (D)5
6(已知两圆的半径分别为 R、 r,且圆心距为 d,若 ,则这两圆的位置关系为( )
(A)外离或外切 (B)相交或内切 (C)外切或内切 (D)内切或内含
7(若圆锥的母线长为 ,底面半径为 ,则圆锥的侧面积是( )
(A)6 (B)12 (C)18 (D)24
9、方程? ? ? ? 中,有解的方程有( )个。
(A)0 (B)1 (C)2 (D)3
10、若方程 的两根为x1,x2,下列表示根与系数关系的等式中,正确的是( ) (A) (B)
(C) (D)
11. 口袋中放有3个黄球和3个黑球,每个球除颜色外都相同.从中任意摸出两个球,则一个是黄球,一个是黑球的概率是( )
A B C D
二 、填空题(每一题5分 总共20分)
1 、已知方程 的一个根是1,则它的另一个根是________,m的值为_______。 2、已知x1、x2是方程2x2+3x,4=0的两个根,那么:x1+x2= ;x1?x2= ; ;x21+x22= ;
(x1+1)(x2+1)= ;
3、ax2+bx+c=0 (a?0) 的求根公式x,
4两圆的半径比是5:3,外切时圆心距是32cm,当两圆内切时,圆心距为________cm.
三(解答下列各题
1、解方程 :(每小题6分共12分)
x2,2x,3=0
2用公式法解方程(7分)
6=0 2x2 +3x,
12((11分)已知:如图47-3,?O1与?O2相交于A、B,若两圆半径分别为12和5, O1O2=13,求AB的长.
(2004、海口,15分)某水果批发商场经销一种高档水果 如果每千克盈利10元,每天可售出500千克,经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量将减少20千克,现该商场要保证每天盈利6000元,同时又要使顾客得到实惠,那么每千克应涨价多少元,
5(15分)、已知购买甲种物品比乙种物品贵5元,某人用款300元买到甲种物品10件和乙种物品若干件,这时,它得到甲、乙物品的总件数比把这笔款全都购买甲种物品的件数多5件,问甲、乙物品每件各是多少元,
范文二:初三数学考试题
一、选择题(1--6题2分,7--12题3分,共30分)
1、的倒数的相反数是( ) ,8
118,A( B(,8 C( D( 88
2、下列分解因式正确的是( )
322222 A( –a+a=–a(1+a) B(2a–4b+2=2(a–2b) C(a–4=(a–2) D(a–2a+1=(a–1)3、将图2-1围成图2–2的正方体,则图2-1中的红心“”标志所在的
正方形的是正方形是下文体中的( )
,(面CDHE ,(面BCEF ,(面ABFG D(面ADHG
25、在平面直角坐标系中,将抛物线先向右平移2个单位,yx,,4
再向上平移2个单位,得到的抛物线的解析式是( )
x2222 B( C( D(4、使分式 A(yx,,,(2)2yx,,,(2)2yx,,,(2)2yx,,,(2)2x,24、有意义的x的取值范围为 ( )
x,2x,,2x,,2x,2A( B( C( C(
211x>,,,420,,x,6、不等式组的解在数轴上表示为( )
A、 B、 C、 D、 7、甲队修路120 m与乙队修路100 m所用天数相同,已知甲队比乙队每天多修10 m,设甲队每天修路xm.依题意,下面所列方程正确的是
120100120100 A(, B(, xxx+10x,10
120100120100 C(, D(, xx+10xx,10
8、如图,在梯形ABCD中,AD?BC,E、F分别是AB、CD的中点,
则下列结论:
?EF?AD;?S?ABO=S?DCO;??OGH是等腰三角形;
?BG=DG;?EG=HF(
其中正确的个数是( )
A(1个 B(2个 C(3个 D(4个
ABCD9、如图4,正方形的边长为10,四个全等的小正方形的对称中
ABCDABCD心分别在正方形的顶点上,且它们的各边与正方形各边平行或垂直(若小正方形的边长为
yy010,x?,且,阴影部分的面积为,则能反映与之间函数关系的大致图象是( ) xx
x y y y y D A 100 100 100 100
x x x x C B O O O O 10 10 5 10 10 图4 A( B( C( D( 2210、如果关于x的一元二次方程有两个不相等的实数根,那么k的取值范围是( ) kxkx,,,,(21)10
1111,,,k,,A.k, B.k,且k,0 C.k, D.且k,0 4444
11、如图4,在矩形中截取两个相同的圆作为圆柱的上、下底面,剩余的矩
形作为圆柱的侧面,刚好能组合成圆柱(设矩形的长和宽分别为y和x,则
y与x的函数图象大致是( )
12、已知二次函数y=ax2+bx+c(a?0)的图象如图所示,有下列5个结论:
?abc,0;?b,a+c;?4a+2b+c,0;?2c,3b;?a+b,m(am+b)(m?1的实数)( 其中正确的结论有( )
A(2个 B(3个 C(4个 D(5个
二、填空题(每题3分,共18分)
313、5,π,–4,3.1415926这四个数中,最大的数是错误~未指定书签。_________________ 14、现有两个不透明的袋子,其中一个装有标号分别为1、2的两个小球,另—个装有标号分别为2、3、4的三个小球,小球除标号外其它均相同,从两个袋子中各随机摸出1个小球,两球标号恰好相同的概率是 。
215、点、是二次函数的图象上两点,则与的大小关系为 Ay(2,)By(3,)yyyyxx,,,2112121
(填“,”、“,”、“,”). ___________y2
22216、已知x = 1是一元二次方程的一个根,则 的值x,mx,n,0m,2mn,n
为 (
17、如图,三个边长均为2的正方形重叠在一起,O、O是其中两个正方12
形的中心,则阴影部分的面积是__________
18、如图9,给正五边形的顶点依次编号为1,2,3,4,5.若从某一顶点开始,沿正
五边形的边顺时针行走,顶点编号的数字是几,就走几个边长,则称这种走法为
一次“移位”。如:小宇在编号为3的顶点时,那么他应走3个边长,即从3?4?5?1为
第一次“移位”,这时他到达编号为1的顶点;然后从1?2为第二次“移位”.
若小宇从编号为2的顶点开始,第12次“移位”后,则他所处顶点的编号是____________. 三、解答题(本大题共8个小题,共72分(解答应写出文字说明、证明过程或演算步骤)
x12A,B,C,,,.19、已知将它们组合成或A,B,C的形式,请你从中任(A,B),C2x,x,x,242
选一种进行计算,先化简,再求值其中((本题8分) x,3
20、为更好地宣传“开车不喝酒,喝酒不开车”的驾车理念,某市一家报社设计了如右的调查问卷(单选).
在随机调查了奉市全部5 000名司机中的部分司机后,统计整理并制作了如下的统计图:(本题8分)
根据以上信息解答下列问题:
(1)补全条形统计图,并计算扇形统计图中m= ;
(2)该市支持选项B的司机大约有多少人,
(3)若要从该市支持选项B的司机中随机选择100名,给他们发放“请勿酒驾”的提醒标志,则支持该选项的司机小李被选中的概率是多少?
21、如图,在Rt?ABC中,?B=90?,BC=5,?C=30?.点D从点C出发沿CA方向以每秒2个单位3
长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t,0).过点D作DF?BC于点F,连接DE、EF.(本题8分)
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗,如果能,求出相应的t值;如果不能,说明理由.
(3)当t为何值时,?DEF为直角三角形,请说明理由.
22、如图,有一个可以自由转动的转盘被平均分成3个扇形,分别标有1、2、3三个数字,小王和小李各转动一次转盘为一次游戏,当每次转盘停止后,指针所指扇形内的数为各自所得的数,一次游戏结束得到一组数(若指针指在分界线时重转)((本题8分)
(1)请你用树状图或列表的方法表示出每次游戏可能出现的所有结果;
2(2)求每次游戏结束得到的一组数恰好是方程x-3x+2=0的解的概率
23、2013年4月20日,四川雅安发生7.0级地震,给雅安人民的生命财产带来巨大损失(某市民政部门将租用甲、乙两种货车共16辆,把粮食266吨、副食品169吨全部运到灾区(已知一辆甲种货车同时可装粮食18吨、副食品10吨;一辆乙种货车同时可装粮食16吨、副食11吨((本题9分)
(1)若将这批货物一次性运到灾区,有哪几种租车方案,
(2)若甲种货车每辆需付燃油费1500元;乙种货车每辆需付燃油费1200元,应选(1)中的哪种方案,才能使所付的费用最少,最少费用是多少元,
24、已知,在平面直角坐标系xOy中,点A在x轴负半轴上,
8点B在y轴正半轴上,OA=OB,函数y=? 的图象与线段ABx
交于M点,且AM=BM(
(1)求点M的坐标;
(2)求直线AB的解析式。
25、如图1,在?ABC中,?A=36?,AB=AC,?ABC的平分线BE交AC于E((本题10分) (1)求证:AE=BC;
(2)如图(2),过点E作EF?BC交AB于F,将?AEF绕点A逆时针旋转角α(0?,α,144?)得到?AE′F′,连结CE′,BF′,求证:CE′=BF′;
(3)在(2)的旋转过程中是否存在CE′?AB,若存在,求出相应的旋转角α;若不存在,请说明理由(
226、如图,已知抛物线y=x+bx+c的图象与x轴的一个交点为B(5,0),另一个交点为A,且与y轴交于点C(0,5)(
(1)求直线BC与抛物线的解析式;
(2)若点M是抛物线在x轴下方图象上的一动点,过点M作MN?y轴交直线BC于点N,求MN的最大值;
(3)在(2)的条件下,MN取得最大值时,若点P是抛物线在x轴下方图象上任意一点,以BC为边作平行四边形CBPQ,设平行四边形CBPQ的面积为S,?ABN的面积为S,且S=6S,1212求点P的坐标((本题12分)
范文三:初三数学考试题
初三数学期末考试题
一、选择题(有且只有一个答案是正确的)(每小题4分,共56分)。
1.平面直角坐标系内点(4,-7)关于x轴对称点的坐标是( )
A、(-4,7) B、(4,7) C、(-4,-7) D、(4,-7)
0 2.锐角A大于60,则有( )
A、 <><1><>< c、=""><><1><><1>
3.三角形的外心一定在该三角形内部的三角形是( )
A、等腰三角形 B、锐角三角形 C、直角三角形 D、钝角三角形 4.一次函数y=mx-n的图象如图,则下面结论正确的是( )
A、m<0,><0><0, n="">0
C、m>0, n>0 D、m>0, n<0>
25.已知方程2x+3=5 -3x,若设=y,则原方程可化为( )
2222 A、y+5y+6=0 B、y-5y-6=0 C、y-5y+6=0 D、y+5y-6=0
6.如图,?O是ΔABC的内切圆,D、E、F是切点,BC=8cm, ΔABC的周长是24cm, 则AE的长是( )
A、6cm B、4cm C、5cm D、8cm
7.已知sinα+cosα=m, sinα?cosα=n, 则m ,n的关系是( )
22 A、m=n B、m=2n+1 C、m=2n+1 D、m=1-2n 8.如果两圆只有两条公切线,则两圆的位置关系是( )
A、相交 B、外切 C、外离 D、内含
9.下列命题中,正确的是( )
A、在同圆中,等弦对等弧
B、在同圆中,等弧对等弦
C、三点确定一个圆
D、圆心角相等,它们所对的弧相等
00 10.在高为h的山坡上,测得山脚下一建筑物顶端与底部的俯角分别为30和60,用h表示这个建筑物的高是( )
A、h B、 h C、 h D、 h
11.如图,?O交ΔABC于B、C、D、E,圆心O在AB上,直线DF切?O于D,交AB于F,弦DG?AB于H,则下列结论中正确的个数是( )
22(1)DF=FE?FB (2)DF=FH?FO
2 (3)DH=EH?HB (4)AD?AC=AE?AB
A、1 B、2 C、3 D、4
12一矩形窗户,面积为4.8平方米,把它的宽y(米)表示成它的长x(米)的函数,则此函数的图象大致是( )
213.如果以y轴为对称轴的抛物线y=ax+bx+c的图象如图所示,那么代数式b+c-a与零的关系是( )
A、b+c-a=0 B、b+c-a>0 C、b+c-a<0 d、不能确定="">
2214.如果x,x是两个不相等的实数,且满足x-2x=1, x-2x=1,那么x?x等于( ) 12112212
A、2 B 、-2 C、1 D、-1
二、填空题(每小题4分,共16分)。
22 1.已知关于x的方程 (a-1)x-(a+2)x+1=0的两个实数根互为倒数,则a的值为_____________。
2.?O的半径是20cm,弦AB//弦CD,AB与CD间距离为4cm,若AB=24cm,则CD=______________cm。
3.如图所示,?O与?O相交于点A、点B,且AO,AO分别为?O,?O的切线,A是切点,112221若?O的半径r=3cm,?O的半径r=4cm,则弦AB=_____________。 1212
24.二次函数y=ax+bx+c的图象如图所示,则点()在直角坐标系中的第__________象限。
三、(第一小题4分,第2小题5分,共9分)。
00 1.计算:tan60+-2cos30.
2.已知:如图,过?O外一点B作?O的切线BM,M为切点,BO交?O于点A,过点A作BO的垂线,交BM于点P,BO=3,?O的半径为1,求:MP的长。
四、(每小题6分,共12分)。
1.解方程.
2.列方程或方程组解应用题。
甲、乙两城间的铁路路程为1600千米,经过技术改造,列车实施了提速,提速后比提速前速度增加20千米/时,列车从甲城到乙城行驶时间减少4小时,这条铁路在现有条件下安全行驶速度不得超过140千米/时,请你用学过的数学知识说明在这条铁路的现有条件下列车还可否再次提速。 五、(每小题5分,共10分)。
1.已知:如图AB是?O的直径,CD切?O于C,BD?CD于D,
CE?AB于E。
2 求证:CD=AE?EB。
0 2.已知在ΔABC中,BC=6,AC=6,?A=30,求AB的长。
六、(本题8分)。
在直角坐标系中,以x轴上一点P(1,0)为圆心的圆与x轴,y轴分别交于A、B、C、D四点,点C的坐标为
(0, ).
(1)直接写出A、B、D三点坐标;
(2)若抛物线过A、D两点,求这条抛物线的解析式,井判断点B是否在所求的抛物线上,说明理由。
七、(本题9分)。
已知AC,AB是?O的弦,AB>AC,
2 (1)如图1,能否在AB上确定一点E,使AC=AE?AB,为什么,
(2)如图2,在条件(1)的结论下延长EC到P,连结PB,如果PB=PE,试判断PB和?O的位置关系并说明理由。
参考答案:
一、1.B 2.A 3.B 4.B 5.B 6.B 7.C 8.A 9.B 10.D 11.D
12.D 13.B 14.D
详细解答:
6.提示:AE=AF,BD=BF,CD=CE,
?AE= (AE+AF)= (24-BC-BF-CE)=×(24-2BC)=4.
22222 7.提示:?sina+cosa=1, ? (sina+cosa)-2sinacosa=m-2n=1, ? m=1+2n.
13.提示:对称轴为y轴,?b=0, 由图可知,c>0, a<0, c-a="">0, ? b+c-a>0。
二、1. 2. 32 3. cm 4. 三
三、1. 2
2. 连结OM,
?BM是?O的切线,M是切点,?OM?BM,
在RtΔBOM中,BM= ==2 ,
?PA?AB,OA是半径,?PA切?O于A,
?PM=PA, 设PM=x,则PA=x,
在RtΔOMB中,sinB==
在RtΔPAB中,sinB= =, ?PB=3x,
? MB=x+3x=4x, ?4x=2,
x= 即MP=。 ?
四、1.解:原方程可化为
2 即 , 设, 则原方程可化为:2y-3y-5=0
解得y=-1, y= , 当y=-1时,, 12
2 去分母整理,得x+x+1=0
解这个方程,?Δ<0, 方程无解。="">
2 当y=时, , 去分母整理,得2x-5x+2=0
解得x=2, , 1
经检验,x=2, 都是原方程的根。 1
? 原方程的根是x=2, 。 1
2.解:设列车提速前速度为x千米/时,
则提速后速度为(x+20)千米/时,
依题意得:, =4
2 整理得:x+20x-8000=0,解这个方程得:x=-100, x=80, 12
经检验x=-100, x=80都是原方程的根, 12
但x=-100不合题意,舍去, ? x=80,
这时80+20=100,即列车提速后速度为100千米/时,
因为这条铁路的安全行驶速度不得超过140千米/时,
100<140, 所以列车在这条铁路现有的条件下还可以再次提速。="" 五、="">
1.证明:连结AC,BC,
0 ?AB是?O的直径,??ACB=90,
2 ?CE?AB于E,?CE=AE?EB,
?CD切?O于C,??BCD=?A,
00 ??A+?ACE=90,?BCE+?ACE=90,
??A=?BCE,??BCD=?BCE,
0 ??BDC=?BEC=90,BC=BC,
?ΔBDC?ΔBEC,?CD=CE,
2 ?CD=AE?EB。
2.解:
(i)当?B为锐角时,
作CD?AB于D,在RtΔADC中,
0 AD=ACcos30=6? =9,
CD=AC=3 ,在RtΔCDB中,
由勾股定理可得:BD=3,?AB=AD+BD=12。
(ii)当?B为钝角时,
作CD?AB的延长线于D,
在RtΔACD中,CD=AC=3 ,
0 AD=AC?cos30=6? =9,
在RtΔCBD中,由勾股定理可得:BD=3,
?AB=AD-BD=9-3=6。
六:分析:连结PC,根据P点、C点的坐标易求PC=2,则A(-1,0)、B(3,0),
又D与C关于x轴对称,?D(0,)。
2 第2问,将A、D两点的坐标代入到解析式y=x+bx+c中,求得b、c,然后再将x=3代入,
即可判定B点是否在抛物线上。
解:(1)A(-1,0),B(3,0),D(0,-).
(2)将A(-1,0),D(0,-)代入
2 y=x+bx+c中,得
解得
2 ?y=x+(1-)x-
当x=3时,
2 y=x+(1- )x-=9+(1- )×3- =12-4 ?0.
2?点B(3,0)不在抛物线y=x+(1- )x-上。 七、(1)在?O上取 ,连结CD交AB于点E,
2 则有AC=AE?AB,如图,连结BC,
??ACE=?ABC,?CAE=?CAE,
?ΔACE?ΔABC,
2 ?= 即AC=AE?AB
(2)连OB,OA,
? ,
? OA?CD,??EAO+?AED=90?,
? PB=PE,??PBE=?PEB=?AED,
又?ABO=?OAE,
??PBE+?ABO=90?,
?OB?PB, ?PB是?O切线。
范文四:初三数学月考试题
第 1页,共 6页
绝密★启用前
吴店中学初三月考数学试题
2017.12.21
学校 :___________姓名:___________班级:___________考号:___________
一、选择题(本大题共 12小题,每题 3分,共 36分) 1. 如图,在矩形 ABCD 中, AB=3, BC=2,点 E 为
AD 中点,点 F 为 BC 边上任一点,过点 F 分别作 EB, EC的垂线, 垂足分别为点 G, H, 则 FG+FH为 (?? )
A. 5
2B. 5
2 C. 310 D. 35 2. 将五个边长都为
3cm 的正方形按如图所示摆放,点 A 、 B 、 C 、 D 分别是四个正方形 的中心,则图中四块阴影面积的和为 (
?? )
A.
3cm2 B. 6cm2 C. 9cm2 D. 18cm2
3. 若一元二次方程 (2m+6) x2+m2? 9=0的常数项是 0,则 m 等于 (?? )
A. ? 3 B. 3 C. ±3 D. 9
4. 已知 m, n是方程 x2? 2x? 2016=0的两个实数根,则 n2+2m的值为于 (?? )
A. 1010 B. 2012 C. 2016 D. 2020 5. 如图, D, E为 △ ABC的边 AB, AC上的点, DE//BC,若 AD :
DB=1:3, AE=2,则 AC 的长是 (?? ) A. 10 B. 8 C. 6 D. 4 6. 若干桶方便面放在桌面上,如图是从正面、左面、上面看到
的结果,则这一堆方便面共有 (?? ) A. 7桶 B. 8桶 C. 9桶 D. 10桶
第 2页,共 6页
7. 已知点 (x1, y1) 、 (x2, y2) 、 (x3, y3) 在双曲线 y=1
x上,
当
x1<>
<>
2<>
时, y1、 y2、 y3的大小关系是 (?? )
A. y1<><>
B. y1
<>
<>
C. y3<>
8. 如图, A 、 B 是曲线 y=3
x经过 A 、
B 两点向 x 轴、 y 轴作垂线段,若 S阴影 =1,则 S1+S2=(?? )
A. 3
B. 4 C. 5 D. 6
9. 如图,点 P 为反比例函数 y=2
xPD⊥ x轴于点
D, △ POD的面积为 k ,则函数 y=kx? 1的图象为 (?? )
A.
B.
C.
D.
10. 在同一平面直角坐标系中,函数 y=kx+k与 y=k
x(k≠ 0) 的图象可能是 (?? )
A.
B.
第 3页,共 6页
C.
D.
11. 如图,一个斜坡长 130m ,坡顶离水平地面的距离为 50m ,那么这个斜坡与水平地
面夹角的正切值等于 (?? )
A. 5
13
B. 12
13C. 5
12
D. 13
1212. 拦水坝横断面如图所示,迎水坡 AB 的坡比是 1: BC=10m,则坡面 AB
的长度是 (?? )
A. 15
m
B.
20
C. 10 m D. 20m
二、填空题(本大题共 8小题,每题 3分,共 24分)
13. 如图,在菱形 ABCD 中, ∠ DAB=60° , AB=2,则菱形
ABCD 的面积为 ______ .
14. 如图, O 是矩形 ABCD 的对角线 AC 的中点, M 是 AD 的
中点,若 AB=3, AD=4,则四边形 ABOM 的周长为 ______ . 15. 如图,已知 E 点在正方形 ABCD 的 BC 边的延长线上,且 CE=AC, AE与 CD 相交
于点 F ,则 ∠ AFC= ______ .
16. 若规定两数 a 、 b 通过运算 ※ 得 4ab ,即 a※ b=4ab. 如 2※ 6=4×2×6=48. 若
x※ x+2※ x? 2※ 4=0,则 x 的值为 ______ .
第 4页,共 6页
17. 如图, 在平面直角坐标系中, 点 A 是函数 y=1
x(x>0) 图象
上一点, 过点 A 作 x 轴的平行线, 交函数 y=k
x(x>0) 的图 象于点 B ,连结 OA 、 OB. 若 △ OAB的面积为 12k 的值为 ______.
18. 如图, 在平面直角坐标系中, 点 A 是函数 y=kx
(x
<0)>
象上的点,过点 A 作 y 轴的垂线交 y 轴于点 B ,点 C 在
x 轴上,若 △ ABC的面积为 1,则 k 的值为 ______ .
19. 如图, 反比例函数 y=3x的图象与一次函数 y=x+2的图
象交于 A 、 B 两点 . 当 x ______ 时,反比例函数的值小于
一次函数的值.
20. 如图,在 △ ABC中, ∠ ACB=90° , AC=4, BC=3, O是
边 AB 的中点,则 sin ∠ OCB= ______ .
三、计算题(本大题共 3小题,每题 4分,共 12分) 21. 解方程:(x? 3)(x? 1) =3.
第 5页,共 6页
22. 计算:(3.14? π) 0+(? 1
2) ? 2+|1? ? 4cos45° .
23. 计算:tan30° cos60° +tan45° cos30° .
四、解答题(本大题共 6小题, 48分)
24. (8分 ) 。已知一元二次方程 (m? 3) x2+2mx+m+1=0有两个不相等的实数根 .
(1)求 m 的取值范围;
(2)当 m 在取值范围内取最小正偶数时,求方程的根.
25. (8分 ) 。受益于国家支持新能源汽车发展和 “ 一带一路 ” 发展战略等多重利好因素,
我市某汽车零部件生产企业的利润逐年提高, 据统计, 2014年利润为 2亿元, 2016年利润为 2.88亿元.
(1)求该企业从 2014年到 2016年利润的年平均增长率;
(2)若 2017年保持前两年利润的年平均增长率不变,该企业 2017年的利润能否超 过 3.4亿元?
26. (8分 ) 。 某商场以 80元 /个的价格购进 1000个保温杯 . 经市场调研, 保温杯定价为 100
元 /个时可全部售完,定价每提高 1元,销售量将减少 5个 . 未卖完的保温杯可以直 接退还厂家 . 要使商场利润达到 60500元,保温杯的定价应为多少元
第 6页,共 6页
27. (9分 ) 。已知反比例函数 y1=k
x
y2=ax+b的图象交于点 A(1, 4) 和点 B(m, ? 2) .
(1)求这两个函数的表达式;
(2)根据图象直接写出一次函数的值大于反比例函数的 值的 x 的取值范围.
28. (9分 ) 。已知:如图, △ ABC是等边三角形,点 D 、 E 分 别在边 BC 、 AC 上, ∠ ADE=60° .
(1)求证:△ ABD∽△ DCE;
(2)如果 AB=3, EC=2
3
DC 的长.
29. 卷面分 (共 6分 )
范文五:初三数学模考试题
山东省济南市长清区初三年级学业水平考试
2015年 5月 数 学 测 试 题
注意事项:
1. 本试题分第 I 卷 (选择题) 和第 II 卷 (非选择题) 两部分, 共 6页, 满分 120分。 考试用时 120分钟。答题前,考生务必用 0.5毫米黑色签字笔将自己的学校、班级、姓名、 考号填写在答题卡和试卷规定的位置上。 2.第 I 卷每小题选出答案后,用 2 B 铅笔把答题卡上对应题目的答案标号涂黑;如需改 动,用橡皮擦干净后,再选涂其他答案标号。
第Ⅰ卷(选择题 共 45分)
一、选择题 (本大题共 15个小题,每小题 3分,共 45分.在每小题给出的四个选 项中,只有一项是符合题目要求的.) 1. -2的绝对值等于 A .-2
B .- 1 2 C . 1
2
D . 2
2. 下列计算正确的是 A .
+
=
B . (ab 2
) 2
=ab4
C . 2a+3a=6a
D . a ? a 3
=a4
3. 如图,∠ 1=40°,如果 CD ∥ BE ,那么∠ B 的度数为 A . 160°
B . 140°
C . 60°
D . 50°
4. 若分式 1
x -1 x 的取值范围是
A . x >1
B . x <1 c="" .="" x="" ≠="" 1="" d="" .="" x="" ≠="">
5. 下列关于 x 的方程有实数根的是 A . x2﹣ x+1=0
B . x2+x+1=0
C . (x ﹣ 1) (x+2) =0
D . (x ﹣ 1) 2+1=0 6. 一种微粒的半径是 0.00004米,这个数据用科学记数法表示为
A . 4×106 B . 4×10﹣ 6 C . 4×10﹣ 5 D . 4×105 7. 一组数据, 6、 4、 a 、 3、 2的平均数是 5,这组数据的方差为
A . 8
B . 5
C .
D . 3.
8. 已知 是方程组 的解,则 a ﹣ b 的值是 A . ﹣ 1
B . 2
C . 3
D . 4
9. 一次函数 y =﹣ 2x +1的图象不经过下列哪个象限
A .第一象限
B .第二象限
C .第三象限
D .第四象限
10. 如图所示的立体图形,它的主视图是
A . B . C .
D .
11. 如图,直径 AB 为 6的半圆,绕 A 点逆时针旋转 60°, 此时点 B 到了点 B ',则图中阴影部分的面积是
A . 6π B . 5π
C . 4π
D . 3π
12. 如图,矩形 ABCD 中, O 为 AC 中点,过点 O 的直线分别与 AB , CD 交于点 E , F ,连 接 BF 交 AC 于点 M ,连接 DE , BO .若∠ COB=60°, FO=FC,则下列结论:① FB ⊥ OC , OM=CM; ②△ EOB ≌△ CMB ;③四边形 EBFD 是菱形; ④ MB :OE=3:2.其中正确结论的个数是 A.1
B.2 C.3
D.4
13. 如图 1, 在平面内选一定点 O , 引一条有方向的射 线 Ox ,再选定一个单位长度,那么平面上任一点 M 的位置可由∠ MOx 的度数 θ与 OM 的长度 m 确定, 有序数对(θ, m )称为 M 点的“极坐标”,这样建
B '
第 11题 图
立的坐标系称为“极坐标系”.在图 2的极坐标系下,如果正六边形的边长为 2,有一边 OA 在射线 Ox 上,则正六边形的顶点 C 的极坐标应记为
A . (60°, 4) B . (45°, 4) C . (60°, 2 ) D . (50°, 2 ) 14.如图,已知直线 a ∥ b ,且 a 与 b 之间的距离为 4,点 A 到直
线 a 的距离为 2,点 B 到直线 b 的距离为 3, AB=.试在直
线 a 上找一点 M ,在直线 b 上找一点 N ,满足 MN ⊥ a 且
AM+MN+NB的长度和最短,则此时 AM+NB=
A . 6 B.8 C.10 D.12
15. 如图, 四边形 ABCD 是边长为 1 的正方形, 四边形 EFGH 是边长为 2的正方形, 点 D 与 点 F 重合,点 B , D (F ) , H 在同一条直线上,将正方形 ABCD 沿 F → H 方向平移至点 B 与点 H 重合时停止,设点 D 、 F 之间的距离为 x ,正方形 ABCD 与正方形 EFGH 重叠部 分的面积为 y ,则能大致反映 y 与 x 之间函数关系的图象是
H
题图 15
2015年 5月初三年级学业水平考试
数 学 测 试 题
注意事项:
第 II 卷必须用 0.5毫米黑色签字笔作答, 答案写在试卷区域内相应的位置, ; 如需改动, 先划掉原来的答案,然后再写上新的答案;不能使用涂改液、胶带纸、修正带。不按 以上要求作答的答案无效。本考试不允许使用计算器.
第Ⅱ卷(非选择题 共 75分)
二、填空题(本大题共 6个小题,每小题 3分,共 18分) 16. 分解因式:3a 2-6a
17. 若 , a b 是方程 2
230x x --=的两个实数根,则 22a b +=_______ 18. 如图,在 □ ABCD 中, AB =6cm ,∠ BCD 的平分线交 AD
于点 E ,则 DE = cm
19. 体育测试中,某班某一小组 1分钟跳绳成绩如下:176, 176, 168, 150, 190, 185, 180(单位:个) ,则这组数据的中位数是 个
20. 如图 1,将正方形纸片 ABCD 对折,使 AB 与 CD 重合,
折痕为 EF .如图 2,展开后再折叠一次,使点 C 与点 E 重合, 折痕为 GH , 点 B 的对应点为点 M , EM 交 AB 于 N ,则 tan ∠ ANE= .
21. 已知在平面直角坐标系中放置了 5个如图所示的正方形 (用阴影表示) , 点 B 1在 y 轴上 且坐标是 (0, 2) , 点 C 1、 E 1、 E 2、 C 2、 E 3、 E 4、 C 3在 x 轴上, C 1的坐标是 (1, 0) ,B 1C 1∥ B 2C 2∥ B 3C 3, 以此继续下去,则点 A 2015到 x 轴的距离是
A
B E
D
(18题图)
三、解答题(共 7小题,共 57分,解答应写出文字说明,证明过程或演算步骤) 22.(本小题满分 7分) (1)计算:(﹣ 1) 2015+-() ﹣
1+
sin45°.
(2)解不等式组 32113x x +>-??
-<>
并把解集在数轴上表示出来。
23. (本小题满分 7分)
(1) 如图,在一次数学课外实践活动中,小文在点 C 处测得树 的顶端 A 的仰角为 37°, BC=20m,求树的高度 AB . (参考数据:sin37°≈ 0.60, cos37°≈ 0.80, tan37°≈ 0.75)
(2) 如图, AB 是半圆的直径, O 为圆心, AD 、 BD 是半圆的弦,且∠ PDA =∠ PBD 求证:直线 PD 是⊙ O 的切线 .
第 23题图
24.(本小题满分 8分 )
小明 7:20离开家步行去上学, 走到距离家 500米的商店时, 买学习用品用了 5分钟. 从 商店出来, 小明发现要按原来的速度还要用 30分钟才能到校. 为了在 8:00之前赶到学校, 小明加快了速度,每分钟平均比原来多走 25米,最后他到校的时间是 7:55.求小明从商 店到学校的平均速度.
25.(本小题满分 8分 )
李老师为了了解所教班级学生完成数学课前预习的具体情况, 对本班部分学生进行了为 期半个月的跟踪调查,他将调查结果分为四类, A :很好; B :较好; C :一般; D :较差.并 将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:
(1)李老师一共调查了多少名同学?
(2) C 类女生有 名, D 类男生有 名,将上面条形统计图补充完整;
(3)为了共同进步,李老师想从被调查的 A 类和 D 类学生中各随机选取一位同学进行“一 帮一” 互助学习, 请用列表法或画树形图的方法求出所选两位同学恰好是一位男同学和一位 女同学的概率.
(1)求直线与双曲线的解析式。 (2)连接 OA ,求 OAB ∠的正弦值。
(3)若点 D 在 x 轴的正半轴上,是否存在以点 D 、 C 、 B 构成的三角形与△ OAB 相似?若存 在求出 D 点的坐标,若不存在,请说明理由
27. (本小题满分9分 ) 如图 1,△ ABC 是等腰直角三角形,四边形 ADEF 是正方形, D 、 F 分 别在 AB 、 AC 边上,此时 BD=CF, BD ⊥ CF 成立.
(1) 当正方形 ADEF 绕点 A 逆时针旋转 θ(0°<><90°) 时,="" 如图="" 2,="" bd="CF成立吗?">
(2)当正方形 ADEF 绕点 A 逆时针旋转 45°时,如图 3,延长 BD 交 CF 于点 G . 求证:BD ⊥ CF ;
(3)在 (2)小题的条件下 , AC与 BG 的交点为
M
, 当 AB=4, AD=时,求线段 BG 的长.
28. (本小题满分9分 ) 如图, 抛物线 y=x 2+bx+c与 y 轴交于点 C (0, ﹣ 4) , 与 x 轴交于点 A ,
B ,且 B 点的坐标为(2, 0)
(1)求该抛物线的解析式.
(2)若点 P 是 AB 上的一动点,过点 P 作 PE ∥ AC ,交 BC 于 E ,连接 CP ,求 △ PCE 面积 的最大值.
(3)若点 D 为 OA 的中点,点 M 是线段 AC 上一点,且 △ OMD 为等腰三角形,求 M 点的 坐标.
长清区 2015年 5月初三年级阶段检测
数 学 试 题 答 案
一、选择题: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 ·· D D B
C
C
C
A
D
C
B
A
C
A
B
B
··
二、填空:16. 3(a-1)2 17. 10 18. 6 19. 176 20. 3/4 21. 3/22014 三、解答题:
22. ⑴解:原式 =-1+2-3+1……………… 2分 =-1 ……………… 3分
(2)由(1)得 x>-1,…… ..1分 由(2)得 x>-2…… 2分 x>-1…… 3分
数轴上表示正确 1分
23(1)解:如图,在直角 △ ABC 中,∠ B=90°,∠ C=37°, BC=20m ∴ tanC=
BC
AB
, …… 2分 则 AB=BC?tanC=20×tan37°≈20×0.75=15(m ) …… 3分 答:树的高度 AB 为 15m . 23. (2)解:连接 OD .
, 2. O B O D
P B D =∴∠=∠ ∴2P D A ∠=∠. ?????????(2分) 又 AB 是半圆的直径, ∴90ADB ∠=°. 即 1290∠+∠=°.
∴190P D A ∠+∠
=°. 即 . OD PD ⊥
∴PD 是⊙ O 的切线 . (4分)
24. 解 :设小明从家走到商店的平均速度为 x 米 /分,
则他从商店到学校的平均速度为 (x+25) 米 /分,根据题意列方程得 3025
30500=++x x
x 解这个方程得 x =
50
经检验 x =50是所列方程的根 .
50+25=75(米 /分) ,所以小明从商店到学校的平均速度为 75米 /分.
25. 解:(1) (6+4) ÷50%=20.所以李老师一共调查了 20名学生. (2) C 类女生有 3名, D 类男生有 1名;补充条形统计图
.
(3)由题意画树形图如下:
从树形图看出,所有可能出现的结果共有 6种,且每种结果出现的可能性相等,所选 两位同学恰好是一位男同学和一位女同学的结果共有 3种. 所以 P (所选两位同学恰好是一位男同学和一位女同学) =2
1
63 26. 解:(1) ∵直线 y=x+b与 x 轴交于点 C (4, 0) , ∴把点 C (4, 0)代入 y=x+b得:b=-4,
∴直线的解析式是:y=x-4; ........................................1分 ∵直线也过 A 点,
∴把 A 点代入 y=x-4得到:n=-1-4 n=-5
∴ A (-1, -5) , ........................................2分
把将 A 点代入 y=
x
m
(x <0)得:m=5, ∴双曲线的解析式是:y="">
5
; ........................3分
(2)过点 O 作 OM ⊥ AC 于点 M , ∵ B 点经过 y 轴, ∴ x=0, ∴ 0-4=y, ∴ y=-4,
初三年级数学试题 第 11 页 共 5页
∴ B (0, -4) ,
AO=26522=+, ....................................4分
∵ OC=OB=4,
∴△ OCB 是等腰三角形,
∴∠ OBC=∠ OCB=45°,
∴在△ OMB 中 sin45°=4OM OB OM =,
∴ OM=22, ..................................5分
∴在△ AOM 中, sin ∠ OAB=1326
22==OA OM ; ..................................6分 (3)存在;
过点 A 作 AN ⊥ y 轴,垂足为点 N ,
则 AN=1, BN=1,
则 AB=2,
∵ OB=OC=4,
∴ BC=24,
∠ OBC=∠ OCB=45°,
∴∠ OBA=∠ BCD=135°, .................................7分
∴△ OBA ∽△ BCD 或△ OBA ∽△ DCB , ∴ CD
BA CB OB =,
∴ 24242244==CD CD 或 ,
∴ CD=2或 CD=16, .................................9分 ∴点 D 的坐标是(6, 0)或(20, 0) . (也可以一种情况一问一分) 27、 解(1) BD=CF成立,理由:
∵△ ABC 是等腰直角三角形,四边形 ADEF 是正方形,
∴ AB=AC, AD=AF,∠ BAC=∠ DAF=90°,
∵∠ BAD=∠ BAC ﹣∠ DAC ,∠ CAF=∠ DAF ﹣∠ DAC , ∴∠ BAD=∠ CAF ,
初三年级数学试题 第 12页 共 5页
初三年级数学试题 第 13 页 共 5页
28. 解:(1)把点 C (0,﹣ 4) , B (2, 0)分别代入 y=x 2+bx+c中, 得 ,
解得
∴该抛物线的解析式为 y=x 2+x﹣ 4. ..............................3分
(2)令 y=0,即 x 2+x﹣ 4=0,解得 x 1=﹣ 4, x 2=2,
∴ A (﹣ 4, 0) , S △ ABC =AB ? OC=12.
设 P 点坐标为(x , 0) ,则 PB=2﹣ x .
∵ PE ∥ AC ,
∴∠ BPE=∠ BAC ,∠ BEP=∠ BCA ,
∴△ PBE ∽△ ABC ,
∴ ,即 , 化简得:S △ PBE =(2﹣ x
) 2.
S △ PCE =S△ PCB ﹣ S △ PBE =PB ? OC ﹣ S △ PBE =×(2﹣ x ) ×4﹣ (2
﹣ x ) 2
=
x2﹣ x+ =
(x+1) 2
+3
∴当 x=﹣ 1时, S △ PCE 的最大值为 3. ..............................6分
(3)△ OMD 为等腰三角形,可能有三种情形:(I )当 DM=DO时,如答图①所示. DO=DM=DA=2,
∴∠ OAC=∠ AMD=45°,
∴∠ ADM=90°,
∴ M 点的坐标为(﹣ 2,﹣ 2) ; .......................7分
(II )当 MD=MO时,如答图②所示.
过点 M 作 MN ⊥ OD 于点 N ,则点 N 为 OD 的中点,
∴ DN=ON=1, AN=AD+DN=3,
又△ AMN 为等腰直角三角形,∴ MN=AN=3,
∴ M 点的坐标为(﹣ 1,﹣ 3) ; ......................8分
(III )当 OD=OM时,
∵△ OAC 为等腰直角三角形,
∴点 O 到 AC 的距离为 ×4=,即 AC 上的点与点 O 之间的最小距离为 . ∵ >2,∴ OD=OM的情况不存在. .....................9分
综上所述,点 M 的坐标为(﹣ 2,﹣ 2)或(﹣ 1,﹣ 3) .
初三年级数学试题 第 14页 共 5页



 无毛刺的不锈钢管
无毛刺的不锈钢管

