范文一:电路微分方程解法
第七章 二阶电路
用二阶线性常微分方程描述的电路称为二阶电路,二阶电路中至少含有两个储能元件——当然含有两个储能元件的电路并不一定为二阶电路,比如两个电容(电感)串(并)联情况。
◆ 重点:
1. 电路微分方程的建立 2. 特征根的重要意义 3. 微分方程解的物理意义
◆ 难点:
1. 电路微分的解及其物理意义 2. 不同特征根的讨论计算
7.0 知识复习
一、二阶齐次微分方程的通解形式
ay ' ' +by ' +cy =0,其特征方程为:ap
2
+bp +c =0,特征根:p 1, 2=-
b 2a
±
b -4ac 4a
2
。
当特征方程有不同的实根p 1、p 2时,y =A 1e p 1t +A 2e p 2t 当特征方程有相同的实根p 时,y =(A 1+A 2t ) e pt
当特征方程有共轭的复根p 1, 2=-δ±j ω时,y =e -(δ+j ω) t =e -δt (A 1cos ωt +A 2sin ωt )
二、欧拉公式
e
j β
=cos β+j sin β
sin(ωt +β) =
e
j (ωt +β)
-e j 2
-j (ωt +β)
-j (ωt +β)
e
-j β
=cos β-j sin β
cos(ωt +β) =
e
j (ωt +β)
+e 2
7.1 二阶电路的零输入响应
7.1.1 二阶电路中的能量振荡
在具体研究二阶电路的零输入响应之前,我们以仅仅含电容与电感的理想二阶电路(即R=0,无阻尼情况)来讨论二阶电路的零输入时的电量及能量变化情况。
+
U 0
C L _
(a) -
_
C L 0
+
(d)
图8-1 L C 电路中的能量振
荡
设电容的初始电压为U 0,电感的初始电流为零。在初始时刻,能量全部存储于电容中,电感中没有储能。此时电流为零,电流的变化率不为零( u C =u L =L
di dt
≠0,∴
di dt
,这样电流将不断增大,≠0)
原来存储在电容中的电能开始转移,电容的电压开始逐渐减小。当电容电压下降到零时,电感电压也为零,此时电流的变化率也就为零,电流达到最大值I 0,此时电场能全部转化为电磁能,存储在电感中。 电容电压虽然为零,但其变化率不为零( i C =i L =I 0=C
du C dt
≠0,∴
du C dt
,电路中的电流≠0)
从I 0逐渐减小,电容在电流的作用下被充电(电压的极性与以前不同),当电感中的电流下降到零的瞬间,能量再度全部存储在电容中,电容电压又达到,只是极性与开始相反。
之后电容又开始放电,此时电流的方向与上一次电容放电时的电流方向相反,与刚才的过程相同,能量再次从电场能转化为电磁能,直到电容电压的大小与极性与初始情况一致,电路回到初始情况。
上述过程将不断重复,电路中的电压与电流也就形成周而复始的等幅振荡。
可以想象,当存在耗能元件时的情况。一种可能是电阻较小,电路仍然可以形成振荡,但由于能量在电场能与电磁能之间转化时,不断地被电阻元件消耗掉,所以形成的振荡为减幅振荡,即幅度随着时间衰减到零;另一种可能是电阻较大,电容存储的能量在第一次转移时就有大部分被电阻消耗掉,电路中的能量已经不可能在电场能与电磁能之间往返转移,电压、电流将直接衰减到零。
7.1.2 二阶电路的微分方程
二阶电路如下,其中电容电压的初始值为u C (0+) =u C (0-) =U 0,电感电流的初始值为
i L (0+) =i L (0-) =0。
图8-2 R 、L 、C 串联的二阶电路
根据该电路列写电路方程为-u C +u R +u L =0 其电路电流为:i =-C 因此:u R =Ri =-RC
du C dt dt
,u R =L
di dt =-LC
d u C dt
22
du C
所以,电路方程为:LC
d u C dt
2
2
+RC
du C dt
+u C =0
7.1.3 二阶电路微分方程的求解
方程LC
d u C dt
22
+RC
du C dt
+u C =0的特征方程为LCp
2
+RCp +1=0。特征根为:
2
p =-
R 2L
±
1?R ?
?-LC ?2L ?
其中:
p 1=-
R 2L R 2L
+
1?R ?
?-LC ?2L ?
1?R ?
?-LC ?2L ?
22
p 2=-
-
由特征根的性质(不等的实数、相等的实数或共轭的复数)就可以确定通解的具体形式。再据电路的初始条件即可得出通解中的待定系数。
7.1.4 二阶电路特征根的讨论
分别讨论特征根的情况。
一、过阻尼情况——非振荡放电过程 1.过阻尼的条件
1L 4L ?R ?
当 ,即R >2(R 2>)时,特征根p 1、p 2为不相等的负实数。 ?>
LC C C ?2L ?
2
此时固有频率为不相等的负实数, 2.过阻尼时的响应
当特征根为不相等的实数时,方程的解的形式为
u C (t ) =A 1e
p 1t
+A 2e
p 2t
其中:
p 1=-
R 2L R 2L
+
1?R ?
?-LC ?2L ?
1?R ?
?-
2L LC ??
22
p 2=-
-
而i =C 而
du C dt
,
du C dt
t =0+
=-
I 0C
,且电路的初始条件,i L (0+) =I 0,有
u C (0+) =U 0,i L (0-) =i L (0+) =0
同时
i =C
du C dt
,
du C dt
t =0+
=-
I 0C
=-
0C
=0
因此,初始条件为:
u C (0+) =U 0,
du C dt
t =0+
=0
代入电路方程u C (t ) =A 1e p 1t +A 2e p 2t 中,就可以解出其中的待定系数,得出
u C (t ) =
U 0p 1-p 2
(p 1e
p 2t
-p 2e
p 1t
)
i L (t ) =-C
du C dt
=
CU 0p 1p 2p 1-p 2
(e
p 1t
-e
p 2t
) =
U 0
L (p 1-p 2)
(e
p 1t
-e
p 2t
)
由此可见,u C (t ) 和i L (t ) 均为随着时间衰减的指数函数,电路的响应为非振荡响应。其中当电流的变化率为零的时刻t m 时电流达到最大值。
di L dt
=p 1e
p 1t
-p 2e
p 2t
=0
而:
t m =
1p 1-p 2
ln p 2p 1
3.过阻尼时的响应曲线
图8-3 非振荡放电过程的响应曲线
二、临界阻尼情况 1.临界阻尼的条件
1L 4L ?R ?
当 ,即R =2(R 2=)时,特征根p 1、p 2为相等的负实数p ;此时固?=
LC C C ?2L ?
2
有频率为相等的负实数,
2.临界阻尼时的响应
当方程的特征根相同时,u C (t ) =(A 1+A 2t ) e pt ,然后可以按照初值求取待定系数;也可以利用非振荡放电过程的解,令p 1→p 2=p =-
R 2L
=-α,取极限得出。
非振荡放电过程的解为:u *C (t ) =根据罗必塔法则:
U 0p 1-p 2
(p 1e
p 2t
-p 2e
p 1t
令p 1→p 2=p =-) ,
R 2L
取极限,=-α,
d (p 1e
u C (t ) =U 0lim
p 2→p 1
p 2t
-p 2e
p 1t
) =U 0(e
p 1t
dp 2
d (p 2-p 1)
dp 2
-p 1te
p 1t
) =U 0e
-αt
(1+αt )
i L (t ) =-C
du C dt
=
U 0L
te
-αt
由此可见,u C (t ) 和i L (t ) 也为随着时间衰减的指数函数,仍然为非振荡响应。其中
t m =
1α
3.临界阻尼时的响应曲线
临界阻尼时响应曲线的变化规律与过阻尼时的情况类似。
t 图8-4 临界阻尼情况的响应曲线
三、欠阻尼情况 1.欠阻尼的条件
1L 4L ?R ?
当 ,即R <2(r><)时,特征根p 1、p="">
LC C C ?2L ?
2
负数。
2.欠阻尼时的响应
?R ?
- 令α=,ω=?,则微分方程的特征根p 1=-α+j ω,p 2=-α-j ω。 LC 2L 2L ??
R
2
1
2
如图所示,设ω与α及ω0之间存在三角关系
α
即 ω0=
δ+ω
22
,β=arctg
ωα
则 α=ω0c o s β,ω=ω0sin β。 根据欧拉公式:
e
j β
=cos β+j sin β
sin(ωt +β) =
e
j (ωt +β)
-e j 2
-j (ωt +β)
-j (ωt +β)
e
-j β
=cos β-j sin β
cos(ωt +β) =
e
j (ωt +β)
+e 2
可将特征根写为:
p 1=-ω0e
-j β
,p 2=-ω0e j β
因此:
u C (t ) =
=
U 0p 1-p 2U 0-j 2ω
?e
??
(p 1e
p 2t
-p 2e
p 1t
)
[-ω
e e
j β(-α+j ω) t
+ω0e
-j β
e
(-α-j ω) t
]
=
U 0ω0
ωU 0ω0
ω
j (ωt +β)
e
-αt
-e j 2
-j (ωt +β)
???
=e
-αt
sin(ωt +β)
i L (t ) =i C (t ) =-C
du c (t ) dt
=
U 0ωL
e
-αt
sin ωt
由此可见,u C (t ) 和i L (t ) 均为幅值随着时间按指数规律衰减的振荡函数,电路的响应为衰减振荡响应。
3.欠阻尼时的响应曲线
4.无阻尼的情况
无阻尼情况是欠阻尼的一种特殊情况。当R =0时,α=0,ω=ω0=为
1LC
,β=
π2
,此时的响应
u C (t ) =U 0sin(ω0t +
U 0ω0L
π2
) C L
i L (t ) =sin ω0t =U 0
sin ω0t
由此可见,u C (t ) 和i L (t ) 均为正弦函数,其幅值不随时间衰减,电路的响应为等幅振荡响应,称为系统的固有频率,当二阶电路的激励为同频率的正弦函数时,称此时电路发生了谐振,其物理意义类似于机械系统的共振。
7.2 二阶电路的阶跃响应与冲激响应
7.2.1 二阶电路的阶跃响应
一、定义
二阶电路在阶跃激励下的零状态响应,称为阶跃响应。
(t )
L 图8-7 R L C 串联的二阶电路的阶跃响应电路
二、求解的步骤
二阶电路的阶跃响应的求取类似于一阶电路的阶跃响应的求取方法。其步骤为 1.计算电路的初始值
i L (0+) 、
di L dt du C dt
0+
u C (0+) 、
0+
2.列写电路微分方程
根据KCL 或KVL 定理列写将电路方程,将其整理成有关电容电压或电感电流(状态变量)的二阶微分方程。
3.计算电路方程的特解
因为是阶跃响应,所以电路方程的特解为常数A ,且A 可以根据初始值最后确定为阶跃激励的强度。
4.计算电路方程的通解
而电路方程的通解为齐次方程的解,因此根据其特征方程求得电路方程得特征根为s 当s 为两个不相等的实数p 1、p 2时,y =A 1e p 1t +A 2e p 2t 当s 为两个相同的实根p 时,y =(A 1+A 2t ) e pt
当s 为两个共轭的复根p 1、p 2时,p 1, 2=-α±j ω时,y =e (α+j ω) t =e -αt (A 1cos ωt +A 2sin ωt ) 。实际上,在此情况下(欠阻尼),可以直接设电路方程的通解为y =Ae -αt sin(ωt +?) 。然后用初始值确定其中的待定系数A 与?。
5.计算电路的初始值
原电路方程的解即为通解于特解之和,再根据电路的初始条件计算出各个待定系数。 这样即可得出电路方程的解。 三、响应曲线
下面给出过阻尼、临界阻尼、欠阻尼三种情况下电路方程的响应曲线,可以看出,三种情况下的稳态值相同。
7.2.2 二阶电路的冲激响应
一、定义
所谓“二阶电路的冲激响应”。实际上是零状态的二阶电路在冲激源的作用下所产生的响应,即为二阶电路在冲激源作用下,建立一个初始状态后产生的零输入响应。
二、解法
因为已知初始状态的二阶电路的零输入响应的求法在前面的章节中已经有详细的介绍,因此要求解二阶电路的冲激响应,关键在于求出冲激激励所产生的电路初始值。
(t )
L 图8-10 R L C 串联的二阶电路的冲激响应电路
7.4 状态方程
在电路系统中,以电容电压及电感电流为变量,列写出的微分方程称为“状态方程”,其中的电容电压及电感电流初始值即为方程的初始值。状态方程在动态系统的研究中具有十分重要的意义。
所谓状态变量,是一组数目最少的、能够确定网络所有变量的动态变量。前面我们介绍了电路方程的列写,实际上是用的是输入-输出方法,也就是选取我们需要研究的单个电路变量,列写它跟输入函数之间的微分方程关系,我们称它为“输入-输出法“。这种方法常常列写出高阶微分方程,其求解存在一些困难,而且一般每一次只能描述一个变量的情况;而列写电路方程的另一种方法是所谓的“状态变量法”,也就是先找出关于一组状态变量的一阶微分方程,然后找到该组状态变量跟激励函数的关系(也为一阶关系),称为“输出方程”。可见对于高阶电路的分析而言,状态变量分析法一方面为我们提供了所有动态变量之间的关系,另外也将求解高阶微分方程的问题转化成为两次一阶方程的求取。
电路的状态方程形式如下:
=Ax +Bw x
为电路中的状态变量向量的一阶导数,其中x x 为电路中的状态变量向量,w 为电路的激励向量(输
入向量),A 、B 分别为相应的系数矩阵。
电路的输出方程形式如下:
r =Cx +Dw
其中r 为电路中的待求响应(输出相量),x 为电路中的状态变量向量,w 为电路的激励向量,C 、D 分别为相应的系数矩阵。可见该方程组为一组代数方程组。
由此可见,状态方程即为有关一组状态变量方程组。 下面我们举例说明。 例1.
因为:
整理,得:
写成标准式: 例2.
因为:
整理,得:
写成标准式:
(t )
L 图8-10 例题1的电路
U L S =i di L R +u C +L dt
C du C dt
=i L
di L 1dt =-R L i L -
L u C +
1L U S
du C 1dt =
C
i L
?R ?i -
1?
L ??-??L L
??i ?1????u =??L ??+C ??
1?C
0??u L ?C ???
?0?U S ? i
(t ) L R
t ) 图8-12 例题2的电路
i u C L =
R +C
du C
2
dt
U R di L S =i L 1+u C +L
dt
du C 1dt
=
1C
i L -
R u C
2C
di L =-
R 1i 11dt
L
L -L
u C +L
U S
?1-
1?
例3.
因为:
整理,得:
写成标准式:
?i ?L
??C R C ??0?
2??i ?u ?=?
?L ?
?+?1?U C ??R 1??-
L
-
1??u ??S C L ??L ?
??
I R
R i (t ) 2 图8-12 例题3的电路
i =
U S -u C 1
R
1
u C 1=R 22C du C 2
dt
+u C 2
u -u C 1
C 1=(
U S R -C du C 11
1
dt
) R 2+u C 2
du C 11dt =
1R u C 1-
2C 2
R u C 2
2C 2
du C 2dt
=-
R 1+R 2R -
R 21R u C 12C 1
R u C 2+
1S
2C 1
L
U ?1
?u -
1?
C 1????=C R C ??u ?0
?
2C 1????u ?C 2??-R 1
??L
-1????u ?+1
C 2???R ?U S ?
1C L ?1
?
范文二:rlc串联电路教案
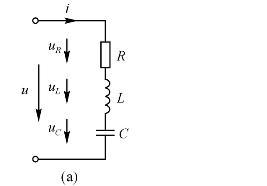
电阻、电感和电容的串联电路
执教者:顾彩凤 一、教学目的
1、掌握RLC串联电路的原理图
2、理解并掌握RLC串联电路端电压与电流的大小关系 二、教学重点
、掌握RLC串联电路的原理图 1
2、理解并掌握RLC串联电路端电压与电流的大小关系 三、教学难点
RLC串联电路端电压与电流的大小关系
四、教学课时
一教时
五、教学过程
1、复习引入新课:纯电阻、纯电感和纯电容电路
2、新授
1)RLC串联电路
a、概念及电路图
R , , , , u, ,,u, ,u, , , ,
i i
, , u
b、电流、端电压及总电压的解析式
2)RLC串联电路端电压与电流的大小关系 a、X>X,则U>U ,电压比电流超前Φ,电路呈电感性,称电感性电LCLC
路。
b、X
路。
c、X=X, 则U=U ,电压和电流同相,电路呈电阻性,称电阻性电路。 LCLC
,,,,, ,,,,, ,,,,,
(C)
3)学生练习
例题:在R-L-C串联电路中,已知电路电流I=4.4A,电源频率为50Hz,
电阻R=30Ω,电感L=445mH,电容C=32μF。
求:(1)电阻、电感和电容两端的电压;
(2)端电压和电流之间的相位差;
(3)判断此电路为何种性质的电路
3、小结
4、布置作业:
书本,143 3、(9) (10) 4、(2)
范文三:微分方程在RLC电路中的应用实践
微分方程在RLC 电路中的应用
Abstract
The relationship of RLC circuit and differential equation has been discussed.
This paper gives two traditional examples of the resolution of the RLC circuit. The pictures drawn by Matlab for the solution of the differential equation are also
contained in this paper.
关键词:RLC 电路、微分方程、Matlab
一、 RLC 电路与二阶微分方程
RLC 电路是一种由电阻(R )、电感(L )、电容(C )组成的电路结构。RC 电路是其简单的例子,它一般被称为二阶电路,因为电路中的电压或者电流的值,通常是某个由电路结构决定其参数的二阶微分方程的解。电路元件都被视为线性元件的时候,一个RLC 电路可以被视作电子谐波振荡器。这种电路的固有频率一般表示为:(单位:赫兹Hz )
fc=1
它是一种带通或带阻滤波器的形式,其Q 值可以由下式得到:
Q = fc
B= 2πfcL=1
wRRLC 电路的组成结构一般有两种:串联型和并联型。
由于RLC 电路通常是由电路结构决定其参数的二阶微分方程,因而完全可以用解微分方程的方法来求解RLC 电路中的各种问题。
二、 应用举例
例1 设有一个由电阻R ,电感L ,电容C 和电源E 串联组成的电路(简称R-L-C 串联电路),其中R 、L 、C 为常数,电源电动势是E= Emsinωt,这里E 及ω 也是常数(图2. 1)。求出R -L -C串联电路中电容C 上的电压Uc(t)所满足的微分方程。
解:设电路中的电流为i(t),电容器所带的电量为Q(t),
自感电动势为EL(t)。
由电学知识可知:
图2.1 RLC串联电路
i= dQdt ,UQdic= C , EL= ?Ldt
因而在R-L-C 电路中各元件的电压降分别为:
UR=Ri=RCUc′
UQc=
C
{UL= ?EL=Ldidt=LCUc′′
根据基尔霍夫电压定律电压定律,得UR+ Uc+ UL=E,将上述方程组代入该式,得:
LCUc′′+RCUc′+ Uc=E
即
Uc′′+ R′1EmLUc+ LCUc= LCsinωt
这就是串联电路中电容 C 上的电压Uc(t) 所满足的微分方程。
如果电容C 经充电后,撤去外接电源(即E = 0),
则上式成为:
URc′′+ ′
LU1c+ LCUc= 0
例2 在如图2.2所示的电路中,先将开关K 拨向A ,使电容充电,当达到稳定状态后再将开关拨向B 。设开关K 拨向A 的时间t>0时回路中的电流i(t)。已知E = 20伏,C = 0.5F, L=1.6H,R=4.8Ω;且i|t=0= 0,di25dt|t=0= 2。
解:在电路R-L-C 中各元件的电压降分别为:
UR=Ri
UQc=
C
UL= ?EL=Ldi{dt
根据基尔霍夫电压定律,得:UR+ Uc+ UL=E 图2.2 RLC暂态电路 将上述各式代入,得:Ldi1dt+Ri+ CQ=E
在上式两边对t 求导,因为i= dt,
因此,得:Ldt2+Rdt+ Ci=0,
即 dt2+Ldt+ LCi=0
将R = 4.8,L = 1.6,C = 0.5代入,得:
d2idi5+3+ i=0 2d2iRdi1d2idi1dQdtdt4
上述方程的特征方程为:
r2+3r+ 54=0
特征根为:r51= ?2 r12= ?2。
所以上述方程的通解为i= C51e?2+ C2e?12t。
为求得满足初始条件的特解,求导数得:
i′= ?5?51?1t
2C1e ? 2C2e
将初始条件 i|di25t=0= 0,dt|t=0= 2代入,得:
C1+ C2=0
{52C125
1+ 2C2= ?2
解得:C25251=? 4 C2= 4因此得回路电流为:
i= ? 25?
4e5t+ 25?14e
图2.3为电流i 的图象.当开关K 拨向B 后,这回路中的反向电流i ,先由0开始逐渐增大,达到最大值后又逐渐趋于零。
图2.3 电流图
三、 小结
例1是将一个具体的RLC 问题建立了微分方程数学模型,而例2中不仅建立了微分方程数学模型,还把微分方程的特解求了出来。
在利用微分方程寻求实际问题中未知函数的三个步骤中,关键是第一个步骤,即根据实际问题建立微分方程,确定初始条件。而建立微分方程的方法,主要是利用导数的几何意义或物理意义直接列出方程。然后求出所列微分方程的通解,并根据初始条件确定出符合实际情况的特解。
由上述例子和分析可知,微分方程在RLC 电路的求解中可以发挥重要的作用,对于一些复杂度不高的RLC 电路可以通过求解微分方程求出其所求值的具体表达形式。
参考文献
[1] 李瑞遐. 应用微分方程. 上海. 华东理工大学出版社,2005年
[2] 秦曾煌. 电工学(上册). 第六版. 北京. 高等教育出版社,2004年
范文四:10、rlc串联电路特性分析
1
《 RLC 串联电路特性分析》仿真实验
一、实验目的
1、学会计算 RLC 串联电路谐振频率 f 0;
2、通过仿真实验探讨 RLC 串联电路在不同工作条件下的性质,探讨串联谐振的特 征,探讨串联谐振电路的选频作用。 二、相关理论知识 (一) RLC 串联电路性质
) (C L X X j R Z Z -+=∠=? Z ――称为电路复阻抗
Z ―― 阻抗模(阻抗大小)
?――阻抗角(总电压与电流的相位差) L X ――感抗, L X L ω=
C X ――容抗, C
X C ω1=
当 X L >XC 时, ? > 0 , u 超前 i ,电路呈感性 当 X L < xc="" 时,="" ?="">< 0="" ,="" u="" 滞后="" i="" ,电路呈容性="" 当="" x="" l="XC" 时,="" ?="0" ,="" u.="" 、="" i="" 同相,电路呈电阻性="" (二)="" rlc="">
谐振定义:总电压和总电流同相。 谐振条件:C L X X = 谐振频率:LC
f π210=
串联谐振特征 :①阻抗最小, Z=R ; ②电流最大, R
U I =。
R
L
C 2
3
u
1
4
i
2
三、实训任务及要求
1、如图 RLC 串联电路,理论计算电路谐振频率 f 0
写出计算公式:
LC
f π210=
2、探讨 RLC 串联电路工作特性
用 Multisim 软件连接电路, 改变电源频率 f , 用数字万用表测量电流 I (有效值) , 用示波器观察电流及总电压波形 , 根据相位关系判断电路性质。
(1)
(2) 测量电流及波形: R
20Ω
L
100uH
C 101nF
2
3
u
1
4
3
根据上述数据表总结: 电路谐振频率 f 0= 。
f=f 0时,电流 , U 、 i 相位关系 ,电路呈 性。
f
f>f
0时,电流 , U 、 i 相位关系 ,电路呈 性。
(3)观察选频特性曲线
打开菜单工具:仿真→分析→交流分析, 设置输出项为电流, 点仿真观察选频特性曲 线:(将曲线截图)
3、电路如下,电源频率 f =5KZH , R=50Ω, L=10μH 。
(1)要使电路谐振,请计算 C =?
(2)怎样进行仿真验证?写出仿真方案及仿真结果。
范文五:rlc串联电路实验报告
篇一:RLC串联谐振电路。实验报告
二、RLC串联谐振电路 目的及要求:(1)设计电路(包括参数的选择)
(2)不断改变函数信号发生器的频率,测量三个元件两端的电压,
以验证幅频特性
(3)不断改变函数信号发生器的频率,利用示波器观察端口电压与
电流相位,以验证发生谐振时的频率与电路参数的关系 (4)用波特图示仪观察幅频特性
(5)得出结论进行分析并写出仿真体会。
二阶动态电路的响应(RLC串联)
可用二阶微分方程描述的电路成为二阶电路。此电路在输入为零值时的响应称为零输入相应,在零值初始条件下的响应称为零状态响应。 欠阻尼情况下的衰减系数? 为:??R
.
1
2L
.
其震荡频率?
d为:?d?;
RLC串联谐振电路条件是:电压U与电流I同相。
z?R?jX?R?j(?L?
1
1
?C
);
当?L?
?C
时,谐振频率为f?f0?
1;
在电路参数不变的情况下,可调整信号源的频率使电路产生串联谐振;在信号源频率不变的情况下,改变L或C使电路产生串联谐振是。电路的频率特性,电路的电流与外加电压角频率的关系称为电流的幅频特性。
串联谐振电路总阻抗Z=R,其值最小,如电源电压不变,回路电流I=U/R,其值最大;改变信号源的频率时,可得出电流与频率的关系曲线;
三.设计原理:
2
一个优质电容器可以认为是无损耗的(即不计其漏电阻),而一个实际线圈通常具有不可忽略的电阻。把频率可变的正弦交流电压加至电容器和线圈相串联的电路上。
若R、L、C和U的大小不变,阻抗角和电流将随着信号电压频率的改变而改变,这种关系称之为频率特性。当信号频率为
f=f0?现象,且电路具有以下特性:
(1)电路呈纯电阻性,所以电路阻抗具有最小值。 (2)I=I。=U/R
即电路中的电流最大,因而电路消耗的功率最大。同时线圈磁场和电容电
时,即出现谐振
厂之间具有最大的能量互换。工程上把谐振时线圈的感抗压降与电源电压之比称之为线圈的品质因数Q。
四.RLC串联谐振电路的设计电路图:
自选元器件及设定参数,通过仿真软件观察并确定RLC串联谐振的频率,通过改变信号发生器的频率,当电阻上的电压达到最大值时的频率就是谐振频率。设计RLC串联电路图如下图:
RLC串联谐振电路
当电路发生谐振时,XL?XC或?L?C1=2.2nF,L1=1mH,R1=510Ω,
3
根据公式f0?
1
?C
(谐振条件)。其中,
可以得出,当该电路发生谐振
时,频率f0?70KHz。RLC串联电路谐振时,电路的阻抗最小,电流最大;电源电压与电流同相;谐振时电感两端电压与电容两端电压大小相等,相位相反。
五.用调节频率法测量RLC串联谐振电路的谐振频率f0
在用Multisim仿真软件连接的RLC串联谐振电路,电容选用C1=2.2nF,电感选用L1=1mH,电阻选用R1=510Ω。电源电压us处接低频正弦函数信号发生器,电阻电压uR处接交流毫伏表。
保持低频正弦函数信号发生器输出电压us不变,改变信号发生器的频率(由小逐渐变大),观察交流毫伏表的电压值。当电阻电压uR的读数达到最大值(即电流达到最大值)时所对应的频率值即为谐振频率。将此时的谐振频率记录下来。
表1谐振曲线的测量数据表
R当频率为70KHz时:
图2 f0?70KHz时的波形图
观察波形,函数信号发生器输出电压us和电阻电压uR
4
相位不同,此时电路呈现电感性。 当频率f0?108kHz时:
图3f0?108kHz时波形图
观察波形,函数信号发生器输出电压us和电阻电压uR同相位,可以得出,此时
电路发生谐振,验证了实验电路的正确,与之前得出的理论值相等。因此证明实验电路的连接是正确的。 当频率为f0?150kHz时:
图 4 f0?150kHz时波形图
观察波形,函数信号发生器输出电压us和电阻电压uR相位不同,此时电路呈现出电容性。
六.用波特图示仪观察幅频特性。
按下图所示,将波特图仪XBP1连接到电路图中。双击波特图仪图标打开面板,面板上各项参数设置如图下图所示。打开仿真开关,在波特图仪面板上出现输出u0的幅频特性,拖动红色指针,使之对应在幅值最高点,此时在面板上显示出谐振频率f0?9.333KHz。
图5 波特图
七.结论与体会:
通过本次是我掌握好了RLC谐振电路的基本规律和它的调整方法,实验中测量谐振
频率的方法有:调节频率法、示波器法、电感电容法。本次实验选择的是调节频率法。本次实验用Multisim仿真软
5
件对RLC串联谐振电路进行分析,设计出了准确的电路模型,也仿真出了正确的结果。并且得到了RLC串联谐振电路有几个主要特征:
谐振时,电路为阻性,阻抗最小,电流最大。可在电路中串入一电流表,在改变电路参数的同时观察电流的读数,并记录,测试电路发生谐振时电流是否为最大。一个正弦稳态电路,当其两端的电压和通过的电流同相位,则称为电路发生谐振,此时的电路称为谐振电路。实现谐振的基本方法是:
角频率?0(或频率f0)不变,调节电感L值和电容C值电感L不变,调节角频率?0(或频率值和电感L值 ;
谐振时,电源电压与电流同相。这可以通过示波器观察电源电压和电阻负载两端电压的波形中否一样的相而得到。
f
)值和电容C值电容C不变,调节角频率?0(或频率f0)
篇二:RLC串联谐振电路电路的研究
实验六 RLC串联谐振电路电路的研究
一、实验目的
(1) 学习测定 RLC 串联电路谐振曲线的方法,加深对串联谐振电路特性的理解。
(2) 学习对谐振频率、通频带和品质因数的测试方法。
二、实验原理
(1) RLC 串联电路(图 4-7-1)的阻抗是电源角频率ω
6
的函数,即
显然,谐振频率仅与元件 L 、C的数值有关,而与电阻R和激励电源的角频率ω无关。
当ω<ωo时,电路呈容性,阻抗角φ<0;当ω>ωo时,电路呈感性,阻抗角φ<0。
(2) 电路处于谐振状态时的特性
图4-7-2图 4-7-3
? 由于回路总电抗XO=ωo-1/ωoC=0,因此,回路阻抗|Z0|为最小值,整个回路相当于
一个纯电阻电路,激励电源的电压与回路的响应电流同相位。
? 由于感抗ωoL容抗1/ωoC相等,所以电感上的电压UL’与电容上的电压UC’数值
相等,相位相差180。电感上的电压(或电容 上的电压)与激励电压之比称为品
质因数Q,即:
L和 C 为定值的条件下,Q 值仅仅决定于回路电阻 R 的大小。
?在激励电压(有效值)不变的情况下,回路中的电流I=US/R为最大值。
(3) 串联谐振电路的频率特性
?回路的响应电流与激励电源的角频率的关系称为电流
7
的幅频特性(表明其关系的图形
为串联谐振曲线),表达式为:
当电路的L和C保持不变时,改变 R 的大小,可以得出不同Q 值时电流的幅频特性
曲线(如图 4-7-2 ) 。显然,Q值越高,曲线越尖锐。
为了反映一般情况,通常研究电流比I/IO与角频率比ω/ωO之间的函数关系,即所谓通用幅频特性。其表达式为:
这里,IO为谐振时的回路响应电流。
图 4-7-3 画出了不同Q 值下的通用幅频特性曲线,显然,Q值越高,在一定的频率
偏移下,电流比下降得越厉害。
幅频特性曲线可以由计算得出,或用实验方法测定。
?为了衡量谐振电路对不同频率的选择能力,定义通用幅频特性中幅值下降至峰值的
0.707倍时的频率范围(图 4-7-3 )
为相对通频带(以B表示),即 B=ω2/ωO-ω1/ωO
显然,Q值越高,相对通频带越窄,电路的选择性越好。
?激励电压和回路响应电流的相角差φ与激励源角频率ω的关系称为相频特性,它可由
公式 :
8
计算得出或由实验测定。相角φ和ω/ωO 的关系称为通用相频特性,如图 4-7-4 所示。
谐振电路的幅频特性和相频特性是衡量电路特性的重要标志。
(4) 串联谐振电路中,电感电压
显然, UL与UC都是激励ω源角频率ω的函数,UL(ω)和UC(ω)曲线如图 4-7-5 所示。当Q>0.707时,UC和 UL才能出现峰值,并且UC的峰值出现在ω=ωC<ωO处, UL的峰值出现在ω=ωL>ωO处。Q值越高,出现峰值处离ωO 越近。
图 4-7-4图4-7-5
三、实验设备
(1) 示波器 1 台
(2) 信号发生器1 台
(3) 晶体管毫伏表 1 只
(4) 电感线圈 1 个
(5) 电容箱 1 只
(6) 电阻箱 1 只
四、实验内容
1、测量 RLC串联电路响应电流的幅频特性曲线的UL(ω)、UC(ω)曲线
实验电路如图 4-7-6 所示。确定元件R、L、C的数值之
9
后,保持正弦信号发生器输出电压 Us(有效值)不变,测量不同频率时的UR、UL和UC。
为了取点合理,可先将频率由低到高初测一次,注意找出谐振频率f0以及出现UC最大值时的频率fC和出现UL最大值时的fL。然后,根据曲线形状选取频率,进行正式测量。记录表格自拟。
2、保持Us和L 、C数值不变,改变电阻R的数值(即改变回路Q值),重复上述实验。
3、测量RLC串联电路的相频特性曲线。保持Us不变,用示波器测量不同频率时Us与UR的相角差(测量方法参见第 3 章中“示波器及其测量方法”有关部分)。记录表格自拟。
4、选做实验
将图 4-7-6 中电容换成另一值,测量其幅频特性。
图 4-7-6
五、注意事项
(1) 每次改变信号电源的频率后,注意调节输出电压(有效值),使其保持为定值。
(2) 实验前应根据所选元件数值,从理论上计算出谐振频率f0和不同Q值时的ωO、ωC、ω
L等数值,以便和测量值加以比较。
(3) 在测量UL 和UC时,注意信号源和测量仪器(晶体
10
管毫伏表或示波器等)公共地线的接。
六、预习与思考题
(1) 实验中,当RLC串联电路发生谐振时,是否有UR=Us和UC=UL?若关系式不成立,试分析其原因。
(2) 可以用哪些实验方法判别电路处于谐振状态,
七、实验报告
(1) 根据实验数据,在坐标纸上绘出不同Q值下的通用幅频特性曲线、相频特性曲线以及UL(ω)、UC(ω)曲线,分别与理论计算值相比较,并作简略分析。
(2) 通过实验总结 RLC 串联谐振电路的主要特点。
(3) 回答思考题。
篇三:RLC串联谐振电路实验报告 .
实验报告
院系:---------------- 年级:2010级 日期:20110428
学号:----------------------
实验名称:RLC串联谐振电路的研究
UO,f(f),UL,f(f),UC,f(f)三条幅频特性曲线如下所示
(图像由origin8.1非线性拟合)
其中输入电压Ui=1.5/?2V?1.06V,C=0.01μF,R=200Ω。
2.从第二张表可知,当电路发生串联谐振是,对应的频率f0=8931Hz,对应的电阻两端电压为U0max=0.644V。
11
通频带宽Δf=9835-1695=1695(Hz),其中,9835Hz和1695Hz对应的电阻电压为U0max/?2=0.455V。
3.Q值的计算:
方法一:由origin软件得出的数据得,当频率达到f0=8931Hz时, Q1=Uc/U=5.26/(1.5/?2)=4.9,Q2=UL/U=5.14/(1.5/?2)=4.8,Q1?Q2
方法二:Q=f0/Δf=8931/1695=5.30
4.R值对通频带宽和Q值的影响。
R值越小,Q值越大,谐振曲线越尖锐,通频带宽越窄。反之Q 值越小,谐振曲线越平缓,通频带宽越宽。
5.两种计算Q值的方法的比较。
方法一中,用电容或电感两端电路谐振时的电压计算Q值,容易受到电路其他部件的影响。比如,导线上的电阻和电感,和电感原件上的电阻对都有分压作用。另外,电容的充放电电压也会作用在电阻上面,导致实际测得的电阻并不精确。
方法二,利用图像计算Q值,误差主要由读数误差导致。并且,图像的拟合效果越接近真实的曲线,则误差越小。
6.谐振的时候,输出电压和输入电压不相等。原因在于,电感和电容上的电阻不可忽略,并且电容的充放电电压和电源电压一起作用在电阻两端。所以测量的结果小于电源电压。
12
7.串联谐振的电路的特性:
电阻,电感,电容两端的电压和电路的频率有关。当频率达到一定值的时候,电路呈现纯电阻状态,此时电阻两端的电压达到最大值,电感和电容两端的电压大小相等,方向相反,为电源电压的Q倍。保持C,L值不变,则电阻R越大,Q值越小。
8.心得体会。
通过这次实验,我初步了解了电路实验的方法,仪器的使用方法。通过本次实验,我进一步对串联谐振有了了解,知道串联谐振在现实中的电路可以产生很大的影响。比如通过L,C两端的电压跟频率有关的特性,可以利用串联谐振电路做成天线接收不同频率的信号。有时,为了防止L,C两端过高的电压对电路元器件造成损害,还应该防止串联谐振的发生,等等。
13



 八秒九七
八秒九七

