范文一:构成物质的基本粒子
构成物质的基本粒子
一、物质的构成
1、物质构成的体系
体积和质量都很 分子 构构分子 成成
物质 构成 构 成概念:带电的原子或原子团
阳离子 阴离子
例1. 下列对分子、原子、离子的认识,正确的是( )
A 、分子是保持物质的最小粒子 B、原子是最小的粒子,不可再分 C 、原子得到或失去电子后形成离子
D 、CO 2和CO 性质的差异主要是由于分子间的间隔不同
例2. 分析各组微粒结构示意图,与表示的意义一致的是 ( ) A .都属于阳离子 B .都属于阴离子
C .属于一种原子 D .属于一种元素
课内训练:
1、夏日的校园,百花盛开,阵阵花香,沁人心脾。花香四溢的现象说明( ) A. 分子是不断运动的分子是由原子构成的 C. 分子之间有一定的间隔 2、结构示意图
表示的微粒是( ) A .原子 B .阳离子
D .阴离子
3
下列叙述错误的是( )
A .铝原子结构示意图的最外层有3个电子
B .元素的正化合价数一定等于原子的最外层电子数
C .核电荷数分别为8和14的元素,组成化合物的化学式为SiO 2
D .同一周期中,原子的核外电子层数相同,最外层电子数从左向右逐渐增多 课堂检测:
1.与元素化学性质有密切关系的是原子的( )
A、原子数 B、中子数 C、电子数 D 、最外层电子数
2.下列符号既能表示一种元素,又能表示一个原子,还能表示一种物质的是( ) A 、 H B、Cu C、O 2+
2 D、Mg 3. 原子中一定含有的粒子是( )
A、质子、中子、电子 B、中子、电子 C、质子、中子 D、质子、电子 4. 某元素的原子最外层有2个电子,该元素( )
A、一定是金属元素 B、是氦元素 C 、一定是非金属元素 D、不一定是金属元素
5.能保持二氧化碳化学性质的最小粒子是 ( )
A.碳原子 B.氧分子 C.二氧化碳原子 D.二氧化碳分子 6.Al 和Al 3+
相同的是( )
A 、所带电性 B、核外电子数 C、化学性质 D、核内质子数
7.某些花岗岩石材中含有放射性元素氡,一种氡原子的质子数为86,中子数为136,这种氡原子的核外电子数为( )
A.50 B.86 C.136 D.222 8.物质的组成、结构和性质关系归纳错误的是( ) A. 核内质子数决定了元素的种类
B. 元素的化学性质与原子最外层电子数目关系密切 C. 原子是化学反应中最小的微粒,因此原子不可再分 D. 物质是由分子、原子、离子等粒子构成
9. 钛和钛合金被认为是21世纪的重要金属材料,它们具有熔点高、密度小、抗腐蚀性能好等优良性能,因此被广泛用于火箭、航天飞机、船舶和化工等。已知钛原子的质子数为22,中子数为26,则钛原子的核外电子数为 ( )
A. 48 B. 26 C. 22 D. 4
10. 学好化学,必须要熟悉物质的组成与分类。下图中分别表示质子数不同的两种原子,则下列各图示表示化合物的是 ( )
11. 在化学世界里没有生命的阿拉伯数字也变得鲜活起来,它们在不同的位置表示着不同的含义。下列化学符号中数字“2”表示的意义正确的是( )
A .Mg 2+
:一个镁离子带2个单位正电荷 B、CO 2:二氧化碳分子中含有氧原子
C.2H :2个氢元素 D、CaO +2
:氧化钙的化合价为+2价 12. 下列现象的微观解释中,不正确...
的是 ( ) A. 氢气和液氢都可做燃料 —— 相同物质的分子,其化学性质相同 B. “墙内开花墙外香” —— 分子在不断的运动 C. 水烧开后易把壶盖冲起 —— 温度升高,分子变大 D. 用水银温度计测量体温 —— 温度升高,原子间隔变大 13. 下列叙述错误的是 ( )
A.分子、原子和离子都能直接构成物质
B.原子中原子核与核外电子的电量相等,电性相反,所以整个原子不显电性 C.决定原子质量大小的主要是质子和电子
D.原子如果得到或失去电子就变成离子 14.某粒子(原子或离子)的结构示意图为 请回答下列问题: (1)该结构示意图中,x 表示 ,y 表示 。
(2)当y=1时,该粒子的名称为
(3)当x-y=10时,该粒子表示 (填“原子”“阳离子”或“阴离子”,下同)当x-y >10时,该粒子表示 ;当x-y <10时,该粒子表示 (4)x=16时,该粒子的符号可能为
(5)当y=O时,可能的粒子符号有
15.A 、B 、C 、D 四种元素,A 元素的原子核外只有一个电子,B 元素的原子得到2个电子以及C 元素原子失去一个电子后,所得粒子均与氖原子具有相同的电子层结构,D 元素的原子第三电子层比第二电子层少一个电子。
(1)写出上述四种元素的元素符号:A B C D (2)写出A 元素与B 元素、C 元素与D 元素组成化合物的化学式: ; 16. 请从H 、C 、O 、Na 等4种元素中选择恰当的元素,组成符合下列要求的物质,并将其化学..式.
填写在相应的空格上: ①能燃烧的固态非金属单质是 ; ②一种有毒的气态氧化物,可用于炼铁的是 ; ③三种元素组成的盐,其溶液呈碱性,还可以做洗涤剂的是 ; ④参与植物的光合作用,可以做农作物气体肥料的是 ;
。
17, 某粒子的结构示意图为(其中n ≠0),请回答下列问题。 (1)n 的最大值为 。
(2)若该粒子带两个单位的负电荷,则其对应的化学符号为 ;由+6价的该元素
形成的常见酸的化学式为 。
(3),若m – n =10,则该粒子对应的常见金属元素有 (写元素符号) 18. 有A 、B 、C 、D 4种元素。A 是地壳中含量最高的元素;B 是组成有机物不可缺少的元素;C 元素的原子核外有4个电子层,最外层电子数等于最内层电子数;D 元素的原子核内只含有1个质子。
(1)写出对应元素的符号:A___________、B___________、C_____________
(2)写出A 与B 元素形成的化合物与A 、C 、D3种元素形成的化合物反应的化学方程式: ____________________________________________________________
19,(1),在FeSO 4和Fe 2(SO 4)3的混合物中已知S 元素的质量分数为23%,则铁元素的质量分数为__________________。
(2),某醋酸溶液中,测得CH 3COOH 和H 2O 所含氧原子数目相等,则该溶液中溶质质量分数为____________。
范文二:1构成世界的基本粒子
1构成世界的基本粒子
书第1章 粒 子 简 介
科学家追求新发现、理解大自然的根本动力是好奇心,通过对自然的仔细
思考和实验而获得进步。为了对实验进行分析,必须首先记录实验结果。最
简单的装置就是人类本身的感观器官,但对于现代科学,这种“自然”的探测器
要么灵敏度不够,要么适用范围不广。以人眼为例,要产生视觉影像,需要至
少20个光子,而一个光电倍增管可以容易地观测单个光子;人眼观察的光谱
集中在可见光区(400~800??),即动态范围只有两倍,而自然界的电磁波频
率从市电、广播到微波、红外辐射、可见光、紫外光、?射线和γ射线,足足跨越
了23个量级!
由此可见,解决自然界的问题,大都需要精确的测量仪器或探测器,才能够
在各种动态范围获得确实的结果。通过发展测量方法和探测器技术,人类强化
和扩展了自身的感观能力。在许多情况下,需要采用新的、特定的探测器,而且
通常不止一种测量。时至今日,还没有一种多功能探测器能够同时测量所需的
所有参数。
为了深入研究微观领域的科学规律,人们需要“放大”器。放大的程度,或者
说可观测到的微观尺度,由探测方法相应的波长决定,例如若使用可见光去探
测,精度约为0.5μ?。当今粒子物理研究采用的“放大”器是各种加速器及其上
的探测器。由于微观粒子的波长和动量成反比(德布罗意关系),因而动量越高
的粒子能够探测的结构越精细。目前,人类可分辨的空间尺度可达10-17??,比
光学显微镜高了十万亿(1013)倍。而在宇观领域,为了研究宇宙的结构,需要探
测、记录的能量范围从约100μ??(宇宙微波本底辐射水平)直至10
20??(高能宇
宙射线)。
为了研究所有这些(与原子核和粒子物理相关的)问题,探测器需要对粒子的
各种参数诸如能量、动量、速度、时间和空间坐标进行测量,并需进一步鉴别粒子的
特性。这就需要多种不同探测技术的综合应用。
?1?
1.1 构成世界的基本粒子
在正式开始讨论粒子探测技术之前,首先需要给要研究的对象???粒子???
做一些界定。
当人们试图了解所处的宇宙(或世界)的各种现象以及其中的内在规律时,很
自然地就会提出两个基本的问题:“宇宙是由什么构成的”,以及“是什么使它们结
合(成宇宙)的”。这也是现代物理学的根本问题。人类对这个问题的认识经历了
很长的时间,并随着现代物理学的发展而逐渐深入、透彻。
自然界有着几乎无穷尽的各种各样的事物,人类很早就发现,这些事物虽
然形式多样,但都可以找到某些相同或类似的性质,因此逐渐意识到世界是由
一些共同的基本单元构成的。在这里我们讨论的“基本单元”一词,其含义是
该事物不具有内部结构(也就是说,不能分割为更小更“基本”的事物)。早在
古希腊时期,恩培多克勒(??????????)就认为世界是由地、气、水、火四种基本
元素构成的。在古代中国和印度,也有类似的思想(在中国,基本元素是金、
木、水、火、土,即五行;而在印度,则是空、气、火、水、土)。在公元前400年左
右,希腊学者德谟克里特(??????????)提出分割物质碎片有小到不可再分的观
念,并用原子(????)代表构成世界的最小单元。但由于客观条件的限制,在很
长的时期内人们无法通过实验证实这些想法。直到1900年左右,由于现代物
理学的迅速发展,人们才开始对真正意义上的原子有所认识。起初原子被设 想为一个疏松的球体,电荷随机分布在内部并不断移动。但很快地,人们就发 现原子可以按其化学性质进行分类(如元素周期表),这意味着存在更基本的 单元,这些基本单元按不同的组合方式构成了具有不同化学性质的原子。随 后的卢瑟福(??????????)散射实验则直接证明了原子存在内部结构,由一个
体
积很小但致密的核与其外笼罩的电子云构成,原子核带正电,而电子带负电。 紧接着人们又发现原子核是由带正电的质子和不带电的中子紧密结合而成 的。那么,是否质子和中子就是最基本的粒子呢?答案是否定的。到了20世 纪60年代,随着实验手段的发展,物理学家发现质子和中子内部存在着更精 细的结构,它们是由更小的单元???夸克(?????)???构成的。到目前为止,夸 ?2?
粒子探测技术 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
? ? ? ? ? ? ? ? ? ? ? ? ? ?
克、电子(及其他轻子)仍可看作几何上的点粒子,没有更进一步的内部结构, 因此我们认为它们就是基本粒子?。图1.1.1给出了从原子到夸克的空间尺
度
的变化。
图1.1.1 原子、原子核、质子和夸克、
电子的空间尺度(其中夸克和电子的大
小由于实验条件的限制只给出了上限)
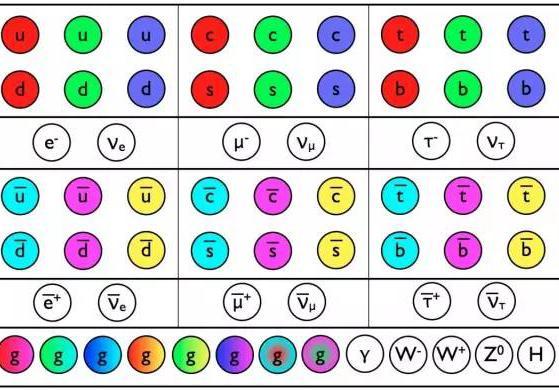
图1.1.2 基本粒子图表
随着加速器等有力工具的出现和发展,人们已经发现了几百种微观粒
子,它们绝大多数都不是基本粒子,而是由基本粒子通过一定的相互作用结
合而成。根据目前的理论(指的是标准模型[1],?????????????),从各种微
观粒子直到整个宇宙,构成它们的基本粒子和相互作用可以归结为以下简
单的几种:6种夸克,6种轻子,以及对应于4种相互作用的规范玻色子。如
图1.1.2所示。夸克是带有分数电荷的费米子,上(??)夸克、粲(?????)夸
克和顶(???)夸克都是带+2/3电子电量的粒子,而下(????)夸克、奇异
(???????)夸克和底(??????)夸克带-1/3电子电量。轻子则包括电子和电
子中微子、μ子和μ子中微子以及η子和η子中微子,电子、μ子和η子都带
有单位电子电量,而中微子都不带电。轻子均为费米子。此外,夸克和轻子
还存在相应的反粒子,正反粒子有相同的质量、自旋和同位旋,但电荷、重子
数、轻子数、奇异数、粲数等则相反。这些就是已知的所有基本粒子,更详细
的数据可参考文献[2]。
?3?
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 第1章 粒子简介
? 但随着物理理论的发展,人们对夸克和电子(及其他轻子)是否是最基本的粒子也存在怀疑???尽
管实验上还无法证明。
需要指出,由于夸克禁闭效应的关系,人们还没有直接观测到自由夸克。 不过,我们在本书中将要讨论的粒子探测,并不仅仅限于基本粒子,而是包括 了亚原子尺度的各种微观粒子。下面将分别加以介绍。
1.2 粒 子 的 分 类
根据粒子的性质和参与相互作用的情况等,可有不同的粒子分类方法。例如, 按照自旋可将粒子分为费米子(具有半整数自旋的粒子)和玻色子(具有整数
自旋
的粒子)两类。这里介绍按照粒子参与相互作用的性质来分类。这样可把粒
子分
为三大类:强子、轻子和场粒子。
强子
强子(??????)是参与强相互作用的粒子,由数个夸克(反夸克)组成。尽 管夸克带分数电荷,但组合后的强子电荷总是电子电量的整数倍。强子的种 类非常多,但根据其自旋是整数或半整数可以分为两大类,即介子(?????)和 重子(??????)。介子由一个夸克和一个反夸克组成,而重子由三个夸克构成, 例如π+介子由上夸克和反下夸克组成,质子(重子)则由两个上夸克和一个
下
夸克构成。习惯上,带有奇异数(即含有奇异夸克)的重子也称为超子 (???????)。
表1.1.1列出了一些常见的强子种类及其主要性质。
轻子
不同于夸克,轻子(??????)作为基本粒子可以自由存在。电子是稳定的,而μ
子和η子则不稳定,会很快衰变为质量更小的粒子。由于μ子质量比最轻的强
子???π介子???还要小,因此它只能衰变到电子和中微子,而η子则除了可以衰
变为μ子外还可能衰变为强子。
中微子是不带电的轻子,由于不参与强相互作用和电磁相互作用,它和物质的
反应截面极小,因此很难探测。绝大多数中微子都可以自由地穿过地球而不发生
任何相互作用。中微子的质量很小,事实上,在20世纪90年代发现中微子振荡效
应[3]之前,一般认为中微子与光子一样,其质量为零。由于宇宙中中微子的数目很
多,其不为零的质量(尽管很小)将会对宇宙学等领域产生显著影响。目前对中微
?4?
粒子探测技术 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
?5?
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 第1章 粒子简介
?6?
粒子探测技术 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
子的研究是基本粒子物理、宇宙学等方向的重要课题。
表1.1.2列出了所有的轻子种类及其主要性质,反粒子没有单独列出。
场粒子
除了夸克和轻子外,还有一类特殊的粒子,即场粒子(????????????),它们
实际上代表了各种基本粒子之间的基本相互作用。正是这些相互作用将基本
粒子组合在一起,或吸引、或排斥、或衰变、或湮灭,共同构成了现在的世界万
物。常见的相互作用有很多种,如摩擦、磁力、重力等等,但它们可以归结为四
种最基本的相互作用,分别是强相互作用、弱相互作用、电磁相互作用和引力
相互作用。一个基本粒子对另一个基本粒子存在作用力,或者换句话说,这两
个基本粒子之间通过交换场粒子从而发生相互影响。相互作用是通过场粒子
传播的,场粒子只作用于特定种类的物质粒子(如电磁相互作用的场粒子只作
用于带电粒子)。
强相互作用的场粒子(规范玻色子)是胶子,弱相互作用是?0和 ??中间
玻色子,电磁相互作用是光子,引力则是引力子。其中引力子由于引力作用强
度太低,还没有被实验观测到。表1.1.3列出了所有的场粒子种类及其主要
性质。
1.3 粒 子 的 寿 命
绝大多数粒子都是不稳定的,并很快衰变为质量较小的强子或轻子。单个粒
子何时衰变与其他粒子无关,是一个随机过程。但大量同种类粒子的衰变则显示
出一定的统计规律。在?到?+??时间段内衰变的粒子数-??应与时间间隔??
和?时刻尚未衰变的粒子数?成正比,即
-??=λ??? (1.1.1)
式中λ=1/η称为衰变常数,积分后有
?=?0?-λ? =?0?-?
/η (1.1.2)
λ具有时间倒数的量纲,相应的η具有时间的量纲,代表了粒子产生后到衰
?7?
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 第1章 粒子简介
?8?
粒子探测技术 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
变时为止平均存在的时间,是粒子的基本属性之一,称为粒子的寿命。在讨
论同位素衰变时,也常用半衰期η1/2来表述核素的寿命,它指的是不稳定核
素衰变到原来数目的一半时需要的时间,半衰期和寿命之间有简单的关
系式
η1/2=0.693η
粒子寿命与引起粒子衰变的相互作用类型有关,一般说来,弱衰变的寿命为
>10-14?,电磁衰变的寿命为10-20~10-14?,强衰变的寿命为10-25~10-20?。所
有强子中,只有质子和束缚在原子核内的中子是稳定的(自由中子不稳定,见表
1.1.1)。而轻子中也只有电子是稳定的。
某些类型的原子核也会衰变。不同于粒子衰变,可衰变的原子核相对容易
获得,并具有较长的寿命,因此在许多领域如工业、医学、化学等行业有广泛的
应用。
原子核的衰变主要通过以下几种方式,α(即氦核)衰变、β(即电子)衰变和γ衰
变。α衰变的过程可以表示为
?
??? ??-4?-2?′?-2+42?? (1.1.3)
目前已知有400多种核具有α放射性,其中绝大部分发射几种不同能量的α射
线,只有个别核素发出单能α射线。核素衰变产生的α射线能量通常在4~
9???之间。β衰变是原子核中的质子和中子相互转变时产生的,可以表示为以
下几种形式
?
??? ???-1?′?+1+β
++ν?
?
??? ???+1?′?-1+β
-+?ν?
?
???+?-???-1?′?+1+ν
?
?
??
(1.1.4)
它们分别代表β
+、β
-和电子俘获(??)衰变。已知的β放射性核素有一千多
种。β衰变产生的电子能量不是单一的,而是连续分布的。原子核衰变发射 α射线或β射线后,通常处于激发态,随即就会放出γ光子而跃迁到较低的 能级,所以γ衰变往往是伴随着α衰变或β衰变之后产生的。γ衰变的能量 是单一的。目前所知的γ放射性核素有两千多种。常见的放射性核素列在 附录中。
?9?
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
? ? ? ? ? ? ? ? 第1章 粒子简介
1.4 重 离 子
重离子一般指的是电荷数大于2倍电子电量的原子核或离子。某种元素的原
子核通常表示为????,其中?是元素的化学符号,?为质子数(即原子序数),?
为
中子数,?=?+?为核子数(即核的质量数)。因而对于重离子,有?>2。重离
子存在于宇宙线中,也可以通过将原子的核外电子剥离而产生。
重核裂变时产生核裂片,也叫裂变碎片,它也是重离子的一种。核裂片的质量
数一般在72到170之间,其分布比较复杂,与裂变重核的原子序数和激发能
量有
关[4]。例如慢中子引起的235?原子核分裂产物的质量分布显示两个明显的
峰,分
别叫轻碎片和重碎片,对应的平均质量数为96和139。
参 考 文 献
[1] ?????????.????????????????????????????????????[?].??????????????,1961,
22:579
588;????????.???????????????[?].????????????????????,1967,19:
1264
1266;??????.????????????????????????[?]//??????????.???????????
????????????????????????.?????????:??????????????????,1968;????????
?,???????????,???????.?????????????????????????????????????????[?].
???????????????,1970,2:1285 1292.
[2] ?????,????(?????????????????).??????????????????????????[?].?????????
????????,2006,33:1 1232;????://???.???.???/.
[3] ???????,????(????????????????????????????).?????8???????????????
????????????????1258??????????????????????????[?].????????????????????,
2001,86:5651 5655;???????,????(???????????????).????????????????
??????ν?+?
??+?+?-??????????????????????8???????????????????????????
?01?
粒子探测技术 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
? ? ? ? ? ? ? ? ? ? ? ? ? ?
???????????????????[?].????????????????????,2001,87:071301.
[4] ?????????,???????? ?.?????????????????????[?].??????????????
??????????????,1974,24:151 208.
习 题
1.强度为1??的60??(钴60)放射源的质量是多少?η1/2=5.26年。
2.放射性强度为10???的32?(磷32)经过30天,它的放射性强度变为多少?
η1/2 =
14.3天。
3.同位素82??的放射性强度在5小时后减弱了9.7%,衰变产物是稳定的元素,试确定它
的平均寿命和半衰期。
4.210??(钋210)是α放射性元素,137??(铯137)是β
-放射性元素,22??(钠22)是β
+放射性
元素,125?(碘125)是?壳层俘获衰变元素,问它们的衰变产物是什么?γ射线是什么同位素发
出的?它们的放射性能量是多少?
5.比较波长λ=500??的可见光、波长λ=0.1??的硬?射线和137??(铯137)的衰变γ
射线能量。
6.做甲状腺吸碘功能测量时,吸进2μ??的
131?(碘131),设测量的吸碘功能为20%,估计测
量时甲状腺在1秒钟内吸收的放射性能量(忽略γ射线的吸收)。如果甲状腺吸进的这些131?一
直保持没有排泄和增加,一个月后放射性强度还有多少?η1/2=8.04天。
7.一病人内服600????2???4,其中包含1500μ??的
32?,在第一昼夜排出的放射性有
540μ??,而在第二昼夜排出71.9μ??(测量是在采集放射物质后立刻进行
的)。试计算病人服用
??2???4后,两昼夜后尚留存于人体内的32?的百分比。η1/2=14.3天。
8.用延迟符合法研究μ子的衰变,在时间0~2μ?内记录了200次衰变,而在0~6μ?时间
内记录到310次衰变,若衰变服从指数规律,试计算μ子的平均寿命。
?11?
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 第1章 粒子简介
第2章 粒子探测的物理基础
粒子或辐射不能被直接观测到,只有通过它们与物质的相互作用才能间接探
测。不同类型的粒子,其相互作用过程也不相同,如带电粒子(如质子)和中性粒子
(如光子)在物质中的反应就大不一样。从最广泛的角度来看,任何一种(粒子与物质
的)相互作用机制都可以当作某种探测器的原理基础,因而相互作用过程的多样性就
决定了存在着大量探测不同粒子或辐射的装置。值得注意的是,即使对于同一种粒
子,在不同的能量范围内其主要反应机制也不尽相同,因此探测方法也会相应改变。
本章主要介绍粒子探测的一般性物理原理,作为后继章节的物理基础。一些特定
反应的物理机制将在讨论相应的探测器时再加以详细了解。涉及相互作用过程及其反
应截面等性质的公式表述时,一般将直接给出结果(但会对公式的物理含义做一些定性
的讨论),而不去追究其具体的物理推导过程。因为这些结果才是探测器直接需要的。
带电粒子同物质的主要相互作用形式是使物质中的原子电离和激发。对于相
对论性粒子?,辐射过程带来的能量损失也不可忽略。中性粒子需要先经特定的
相互作用产生次级带电粒子,再通过这些次级带电粒子进行探测。例如光子可以
经光电效应、康普顿散射和电子对产生生成带电粒子(电子),通过测量它们的电离
过程就可以探测这些次级电子了。
2.1 带电粒子和物质的相互作用
带电粒子穿过物质时可通过激发(该物质)原子中的束缚电子或电离过程损失
?21?
? 一般指该粒子能量较高,相对论效应起主导作用,β~1。
一定的动能,一般来说,电离过程起主要作用。激发过程可以表示为
??+??????????+??
????+γ
退激发的原子释放出低能光子,某些探测器可以测量到这些荧光光子。电离过程
则是通过散射将一部分入射粒子的能量传给原子中的电子,使之直接摆脱原子的
束缚从而形成电子 离子对。一次散射能够传递的最大动能取决于入射粒子的质
量? 和动量?。给定入射粒子动量
?=??=γ?0β?
其中γ为洛伦兹因子(=?/?0?2,?为粒子能量),β?=?为粒子运动速度,?0
为粒子静止质量。入射粒子传递给一个静止电子的最大动能为[1]
????=
2???2β
2γ2
1+2γ??/?0+(??/?0)2
=
2???2
?20+?2?+2???/?2
(2.1.1)
式中??是电子静止质量。注意上式讨论的是动能而不是总能量,这是因为该电
子已经存在,而不需要(能量)去产生它。在低能情况下
2γ??/?0?1
若入射粒子比电子重(??<?0)?,则公式(2.1.1)可以近似为 ????=2???2β
2γ2 (2.1.2)
例如,一个洛伦兹因子γ=10的μ轻子(?μ?2=106???),相应的总能量为 ?=1.06???,在一次散射中最多可以将约100???的动能传给一个电子 (???2=0.511???)。
对于除电子外其他入射粒子,在任意能量下,式(2.1.1)分母中的平方项 (??/?0)2均可以忽略,因而
????= ?
2
γ?0+?20/2??
(2.1.3)
对相对论性粒子而言,动能??????及????,所以有最大可传递能量 ?31?
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
? ? ? ? 第2章 粒子探测的物理基础
? 比电子重的最轻粒子是μ轻子,其质量也比电子大200多倍,因而总
有????0。
????=
?2
?+?20?2/2??
(2.1.4)
对于μ轻子,上式改写为
????= ?
2
?+11
单位是???。在极端相对论的情况下(???20?2/2??),所有能量可以一次传递 给电子。
如果入射粒子是电子,则以上式(2.1.2)和(2.1.3)的近似不成立。此时有 ????= ?
2
??+?/?2
=?-???2 (2.1.5)
即入射电子将全部动能传递给物质原子中的电子。这个结论和经典非相对论
运动
学中两个等质量的球体对心碰撞的结果是一样的。
2.1.1 电离和激发能量损失
能量损失率
前面的论述已经表明了电子在通过物质时一次散射传递的最大动能与其他
较
重的粒子(?0>??)相比有明显差别。我们首先讨论较重的入射粒子穿过物质 时的能量损失。贝特(?????)和布洛赫(?????)等人给出了入射粒子的平均能
量损
失率公式[2]
-
??
??=
4π???2????2?2 ?
?
1
β
2
1
2
??
2???2β
2γ2????
?2
-β
2-δ( )2 (2.1.6) 其中各参数的意义如下: ????入射粒子电荷量,以电子电量|?|为单位。
?,????所穿越物质的原子序数和原子量,?的单位是?/???。
?????电子质量。
?????经典电子半径 =
1
4πε0
?2
???2
,ε0( )为真空介电常数 。
?????阿伏加德罗常数(=6.022×1023/???)。
????平均激发能,取决于所穿越物质的性质。可近似描述为 ? = 16?0.9??(?>1)。?还与该物质所处的分子态有关,例如,原子态、分 ?41?
粒子探测技术 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
? ? ? ? ? ? ? ? ? ? ? ? ? ?
子态的气态氢和液态氢对应的平均激发能分别为15??、19.2??和 21.8??。?/?随物质元素原子序数变化的详细结果可参考文献[3]。 δ???密度效应修正参数。当粒子能量上升时,其自身电场分布逐渐集中到垂 直于粒子运动方向的平面内,场强增加,因而能够同更远处的物质发生 散射。这种“远程”散射效应带来的能量损失正比于??βγ(对数上升)。 然而,物质在此电场中发生极化,附加的极化电场限制了粒子自身电场 的扩展,从而有效地抑制了这种效应。在非常高的能量下,δ/2= ??(?- ω?/?)+??βγ-1/2,?- 为普朗克常数,?- ω?称为等离子体能量,是
一
个与具体物质有关的常数。正如其名称所表示的,密度效应在致密的物 质中更显著,如铅和铁等,而在正常气压下的气体中,只要能量不是非常
高,密度效应都可忽略。密度效应有很多的近似表述和参数化公式(可 参考文献[4]),这里从略。
式(2.1.6)叫做贝特 布洛赫(????? ?????)公式,平均能量损失率通常也称
为“阻
止本领”(?????????????),或简称为“能量损失”或“能损”。其中一个有
用的常
数是
?=4π???2????2=0.3071
???
?/??2
(2.1.7)
在公式的对数项中,分子部分的2???2β
2γ2正是式(2.1.2)给出的在低能情况下
的最大可传递动能。如果我们采用式(2.1.2)的近似和(2.1.7)的缩写,在入
射粒
子能量较低时????? ?????公式可改写为
-
??
??=
??2?
?
1
β
2 ??
???????
? -β
2-δ[ ]2 (2.1.8)
计算时,能损-
??
??
通常使用的单位是???
?/??2
,相应的??单位为?/??2,代表面质
量密度
??=ρ???
其中ρ为物质密度(单位:?/??3),??为长度(单位:??)。这样选取单位的好处 是能损在很大程度上与物质的具体性质无关。
????? ?????公式是对粒子穿越物质时因电离和激发过程损失能量的一种 近似描述,因而必然存在一定的适用范围。图2.1.1显示了带正电的μ轻子
在穿
越铜时的能量损失。粒子能量直至几百???时,公式(2.1.11)给出的误差仍小
于
?51?
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
? ? ? ? 第2章 粒子探测的物理基础
图2.1.1 μ+在铜内的能量损失与粒子动量和βγ的关系[5] 图中的竖带大致标出了几种不同近似的适用范围。在能量不太低和不太 高的情况下,能损由????? ?????公式描述
10%。然而对于能量很低的粒子,当其运动速度与原子中电子的速度相当时,
公式
不再适用。当粒子运动速度α??β?10
- (3 α= ?22ε0??~
1
137 )为精细结构常数
时,能损正比于β。例如慢速质子在硅介质中的能损为
-
??
???β=
61.2β
???
?/??2
在0.01<><0.05区间,目前尚无令人满意的理论解释,只能依赖一些唯象 的拟合公式。="">
对于β?α?,????? ?????公式均可适用?。在低能部分,能损近似正比于 1/β
2下降,并在βγ~4处达到一个分布很宽的最小值区域。对应于此最小值的
相
对论粒子称为“最小电离粒子”(??????????????????????????,或???)。在较轻的
物质(?/?~0.5)中,最小电离粒子的能损大致为
?61?
粒子探测技术 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
? 但能量很高时(如βγ>1000),辐射损失能量起主导作用,电离和激发能损只占总能量损失的很小
部分。
-
??
?? ????
2???
?/??2
表2.1.1列出了部分材料中最小电离粒子对应的能量损失。其中标准温度和气压
(???)即为0摄氏度和1大气压。可以看出随着物质原子序数的增加,最小电离时
的能损在逐渐减小,这主要是由于公式中?/?的影响。
表2.1.1 一些常见材料中最小电离粒子对应的平均能损(气体处于标准气压和20?下)
吸收材料 -
??
?? ???
???
?/??[ ]2 -???? ???
???[ ]??
氢气(?2) 4.103 0.344×10-3 氦气 1.937 0.242×10-3 锂 1.639 0.875 铍 1.594 2.946 碳(石墨) 1.745 3.952 氮气 1.825 1.473×10-3 氧气 1.801 2.055×10-3 空气 1.815 2.187×10-3 二氧化碳? 1.819 3.596×10-3 氖气 1.724 2.076×10-3 铝 1.615 4.361 硅 1.664 3.877 氩气 1.519 2.121×10-3 钛 1.476 6.701 铁 1.451 11.419 铜 1.403 12.571
锗 1.371 7.298
锌 1.264 9.240
氙气 1.255 3.706×10-3
钨 1.145 22.099
铂 1.129 24.217
铅 1.123 12.746
?71?
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
? ? ? ? 第2章 粒子探测的物理基础 续表
吸收材料 -
??
?? ???
???
?/??[ ]2 -???? ??? ???[ ]??
铀 1.082 20.997
水 1.991 1.991
合成树脂 1.929 2.276 混凝土(水泥) 1.711 4.278 石英(???2) 1.699 4.485
? 测量条件为标准温度(0?)和标准气压。
当βγ>4时,能量损失开始增加,这种增加来自公式(2.1.6)中括号内的对数
项,考虑到????~β
2γ2以及密度效应的修正后,能损上升近似正比于??βγ(忽略
密度效应修正时,正比于2??βγ),因此也称为相对论对数上升。产生对数上升的
主要原因来自粒子穿越物质时的远程相互作用(见前文公式(2.1.6)中密度效应解
释)和(小概率的)大动能转移散射过程,获得较高能量的散射电子称为δ电子或敲
出(????????)电子。在实际应用中,如果排除了这些δ电子事例,则能量损失的相
对论对数上升幅度减少,很快趋于饱和。
????? ?????公式描述的是由于电离和激发过程导致的能量损失,当粒子能
量很高时,辐射能量损失开始起重要作用。通过辐射过程损失的能量正比于入射
粒子的能量,因此在高能情况下(如?>1???),粒子损失能量主要来自辐射能损
的贡献。
图2.1.2显示了几种不同带电粒子(电子、μ轻子、π介子、质子、氘核和α粒子)
在空气中的能量损失情况,以及在不同物质中电离能损随粒子动量的变化。
注意由
于密度效应不同,气体(氦气)中能损的相对论上升幅度比液体和固体物质要大。
????? ?????公式给出的是能量损失的平均值,当粒子穿越薄的吸收体层
时,由于相互作用次数少,能量损失的统计涨落很大。在薄层物质,例如气体中,能
损的分布很不对称,更接近于朗道(??????)分布而非高斯(?????)或泊松
(???????)分布。朗道分布的一个近似形式如下
?(λ)= 1
2?π
????-
1
2
(λ+?-λ[ ]) (2.1.9)
其中λ代表与最概然能损之间的偏差
?81?
粒子探测技术 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
图2.1.2 带电粒子在不同物质中电离能损随粒子动量的变化
λ=Δ?-Δ?
ξ
Δ?为在厚度?的吸收层中的实际能损,最概然能损Δ?则是能损分布中最大
概率
处对应的能量损失,
Δ?=ξ??
2???2β
2γ2
? +
??ξ
?+?-β
2-( )δ
[6]
(2.1.10)
?=0.200,而ξ=(?/2)?
2(?/?)(?/β
2)???,?的单位是?/??2。
以电子穿越1??厚的氩气层为例。由式(2.1.10)可得ξ=1.9???,相应地, 可以计算出一个最小电离粒子在1??厚的氩气层中最概然能损为0.95???,
可
见比平均能损低了很多(2.121???,见表2.1.1)。最概然能损与平均能损的
差别
还可参考图2.1.3。
实际测量的能损分布通常都比朗道分布给出的结果要宽,特别是对很薄的吸 收层。但最概然能损式(2.1.10)仍然成立。 (对于非常厚的吸收层 ???????
2???2β
2γ )2 ,朗道分布的高端尾部大为收缩,能损分布可以用高斯分布近似。 能损的朗道起伏在很大程度上同大动能转移散射过程相关,入射粒子有可能 在单次电离过程中将相当大的能量传递给物质原子中的电子,以至于这种电
离出
的电子有足够的能量产生次级电离过程。如前所述,这种电子被称为δ电子
或敲
?91?
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
? ? ? ? 第2章 粒子探测的物理基础
图2.1.3 薄层吸收体中能量损失的分布(注意横坐标有两套单 位,?分别选取为物质厚度和面质量密度。容易看出最概然能损 与平均能损的差别)
出(????????)电子。δ电子的产生几率很小,其能谱由下式给出[1] ??
??=ξ
??
?2
(2.1.11)
式中要求????????,ξ定义同式(2.1.10)。
当??????时,?是一个与入射粒子自旋有关的量,大小约为1,例如对自旋 为1/2的粒子,?(?)=1-β2?/????,其他自旋情况下的公式可参见文献[1]。
只有在趋近最大可转移动能????时,自旋对?的影响才较为显著,且此时能谱
趋
近于零(??0),因而?也受到运动学约束的限制。
对式(2.1.11)积分,就可得到带电粒子通过路程?后,由于电离作用传给物质 的动能大于?的几率(未归一化)
?(>?)=?
?
?
ξ
??
?2
=ξ?
式中已假设了粒子能量远大于?,故积分上限取为无穷大。
当带电粒子一次通过期间,所涉及的最大能量转移的作用次数很多时,能损
分
?02?
粒子探测技术 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
? ? ? ? ? ? ? ? ? ? ? ? ? ?
布满足泊松(或高斯)分布,也就是说,?(>????)?1,即ξ/?????1,将之代入ξ 的表达式,并取?/??0.5,即得
β
4/(1-β
2)?0.074?
这个公式给出了电离过程分布满足泊松分布的条件(即物质路径?很长)。而
在朗
道分布的情况下,入射粒子在一次通过期间,涉及最大能量转移的作用次数
很少,
也就是要求ξ/?????1,即有
β
4/(1-β
2)?0.074?
这就是电离分布遵从朗道分布的条件(即物质路径?很短,如薄层气体)。例如 50???的非相对论性的质子(β~1/3,β
4/(1-β
2)~1/80),在通过1????-2闪烁
体时,电离损失基本遵从泊松分布。而1???的μ子通过10???? -2闪烁体时,电离
损失则遵从朗道分布(β
4/(1-β
2)~100)。
还要指出,泊松分布和朗道分布是ξ/?????1和ξ/?????1的两种极端情况, 处于它们两者之间的是瓦维洛夫分布,就更为复杂了,读者有兴趣的话可参
阅文
献[6]。
图2.1.4 μ子在硅吸收体中的贝特 布洛赫能损以及两个不同截断
能量下的能损(同时显示的还有当吸收体厚度较薄时朗道分布的最概
然能损Δ?(实际上是Δ?/?)。图中结果没有包括辐射引起的能损)
虽然在薄层吸收体中能损存在很大的朗道起伏,但实际应用中探测器观测到
?12?
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 第2章 粒子探测的物理基础
的起伏通常没有那么大。一般说来,探测器测量的是沉积在其灵敏体积内的那部
分能量,而这部分能量很可能不等于粒子损失的能量。例如,入射粒子将一部分能
量传递给δ电子,而δ电子再通过次级电离将其能量沉积在探测器的灵敏体积内,
但由于灵敏体积的大小有限,δ电子可能在沉积部分能量后就飞离了探测器的灵
敏区,因此测量的能损小于粒子的实际能损。
考虑到上述因素,实际上人们感兴趣的通常是转移动能?小于某个阈值????
的那部分能损。这种截断的平均能量损失率可表示为
-
??
?? ?<????
=??2??
1
β
2
1
2
??
2???2β
2γ2????
?2
-β
2
2
1+
????
?( )??? -δ[ ]2 (2.1.12) ?由式(2.1.7)定义。公式(2.1.13)和(2.1.6)类似,但又不完全相同。因为截
断
很大程度上消除了δ电子的影响,能损分布不再像式(2.1.9)那样有一个明
显的朗
道尾部;如前所述,在计及密度效应的贡献后(注意密度效应参数δ和δ电子
是两
个不同概念),电离和激发能损随能量增加而趋于饱和,这个饱和区叫费米坪,如图
2.1.4所示。
当粒子穿越多种元素构成的化合物或混合物质时,可以看作穿过多个按比例
分布的纯元素层,因此其电离和激发能损可由下式计算
??
??=????
??
?? ?
(2.1.13)
式中??为第?种纯元素的质量比例,
??
?? ?
为该元素的平均能量损失率。由于分
子结构的差异引起的电离常数(激发能)变化可能给式(2.1.11)带来微小修正,但
通常均可忽略。
至此,我们已详细讨论了重(质量比电子质量大)带电粒子穿越物质时因电离
和激发过程所引起的能量损失公式。而当入射粒子是电子时,其能损情况有所不
同,需要单独处理。这一方面是由于即使在很低能量下(???能区)电子因辐射过
程损失的能量也不可忽略;另一方面则是由于在电离过程中,入射粒子与物质原子
中的电子是全同粒子,其散射过程需要特殊处理。
对于电子的电离过程,由于散射后无法区分原初电子和次级电子,其能量传递
和式(2.1.1)不同。考虑一个电子在碰撞后获得?的动能,而另一个电子的动能
是?-???2-?(?为入射电子的总能量),根据全同粒子的特性,能量传递将在
?22?
粒子探测技术 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
0,1
2
(?-???2[ ]) 区间内变化,而不是[0,?-???2]。
此效应很容易在公式(2.1.6)中体现出来,将式中的????(以及2???2β
2γ2?
????)变为新的表达式即可。对于相对论电子,
1
2
(?-???2)可以近似为
1
2
?=
1
2
γ???2,取?=1,则电子的能损公式可近似为
-
??
??=
??
?
1
β
2 ??
γ???2
2? -β
2-δ
?[ ]2 (2.1.14) 其中δ?与之前的定义略有不同。在详细考虑入射重带电粒子和电子之间的
差别,
并计及电子 电子散射的运动学限制和自旋、屏蔽效应后,更精确的电子能损
公
式为
-
??
??= ??
?
1
β
2 ?? γ???2βγ-? 1
?2? +
1
2
(1-β
2)- 2γ-1 2γ2
+
1
16
γ-1( )γ
?
?
?
?
2
对正电子的处理是类似的,不同之处是入射粒子和散射电子的质量相同,但
不
是全同粒子。其能损公式如下
-
??
??= ??
?
1
β
2 ?? γ???2βγ-? 1
?2? -β
2
24
23+ 14
γ+1
+
10
(γ+1)2
+
4
(γ+1)[ ]? ?
?
?
?
?
3
由于正电子是电子的反粒子,那么还有更多一层的考虑。当正电子损失完能
量而
静止下来时,它将和一个电子发生湮灭,产生两个背对背发射的光子,在质心
系中
每个光子的能量都是0.511???。在飞行过程中正电子的湮灭截面为[7]
ζ(?,?)= ?π?2?
γ+1
γ2+4γ+1
γ2-1
??(γ+ γ2-? 1)- γ+3
γ2-?[ ]1
电离产额
入射带电粒子在物质中因激发和电离所损失的能量将产生沿粒子径迹分布的
电子 离子对。这里需要注意的是原初电离和总电离两个概念。原初电离是由入
射粒子通过电离过程直接产生的电子 离子对,而某些获得较多能量转移的电子(δ
电子)可以产生次级电离,所有的次级电离和原初电离合起来构成总电离。
产生一个电子 离子对需要的平均能量(? 值)超过物质的电离能,这是因为
?32?
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 第2章 粒子探测的物理基础
物质原子的内层电子也可参与到电离过程中,入射粒子传递能量的一部分可能因
原子激发而被消耗掉。对于相对论粒子,特定物质的 ? 值基本保持不变;在较低
运动速度时,? 值会略微有所增加。
对于气体,? 值约为30??,但气体的纯度对其影响很大。表2.1.2给出了部
分气体的? 值及最小电离粒子产生的原初电子 离子对数目(??)和总电离数
(??)等参数
[8](注意其中电离能?0 和上一节中的平均激发能?/? 是不同的概 念)。由于实验上很难区分原初电离和次级电离,因此??的具体数值存在一定
的
不确定性。总电离数??可以通过在探测器中沉积的总能量导出 ??=
Δ?
?
(2.1.15)
注意只有当粒子损失的能量全部沉积在探测器中上式才是正确的。 表2.1.2 一些气体的电离能?0,? 值,原初电离数??和总电离数?? (气体处于标准气压和温度下,入射粒子为最小电离粒子) 气体种类 密度ρ[?/??3] ?0[??] ?[??] ??[?? -1] ??[??-1]
氢 8.99×10-5 13.6 37 5.2 9.2 氦 1.786×10-4 24.6 41 5.9 7.8 氮 1.250×10-3 14.5 35 10 56
氧 1.428×10-3 13.6 31 22 73
氖 9.005×10-4 21.6 36 12 39
氩 1.782×10-3 15.8 26 29 94
氪 3.74×10-3 14.0 24 22 192 氙 5.858×10-3 12.1 22 44 307 二氧化碳 1.977×10-3 13.7 33 34 91
甲烷 7.17×10-4 13.1 28 16 53
丁烷 2.67×10-3 10.8 23 46 195
在固体探测器(如半导体探测器)中,入射粒子能损将产生电子 空穴对。在固
体硅和锗中产生一个电子 空穴对所需的能量分别是3.6??和2.85??,远低于表
2.1.2中气体的? 值,这意味着在固体探测器中产生的载流子(电子和空穴)数目
与气体中相比(其载流子为电子和离子)要大得多。因此,沉积相同的能量,固体探
?42?
粒子探测技术 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
测器测得的载流子统计涨落远比气体探测器小。
相应于一定的能量沉积,载流子对的产生是一个随机过程。假设平均有?对
载流子产生,我们可以简单地认为其统计涨落服从泊松分布,即??。然而实际情
况并非如此,载流子对数目的统计涨落一般要比泊松分布给出的值小??倍,??的
值与具体物质有关。此效应由法诺(????)首先发现[9],因而??被称为法诺因子,
它实际上来源于能量守恒定律对载流子产生过程的限制。关于法诺因子我们
在第
3章中还将详细介绍。
需要注意的是,固定能量沉积产生的总电离数起伏和在薄层吸收体内能损的
朗道起伏是完全不同的,后者没有能量守恒产生的附加限制,因而没有法诺因子的
贡献。一般来说,对于将全部能量沉积在探测器灵敏体积内的粒子而言,都需考虑
法诺因子。
表2.1.3列出了一些情况下的法诺因子,可以看出,它对能量分辨率的改善是
很大的。
需要指出,随着探测设备和电子学水平的提高,实际上法诺因子甚至比理论预
期的结果还要小,原因尚不清楚。
表2.1.3 一些常见探测器物质的法诺因子[10]
放 射 源 能 量 吸 收 体 ?
?射线 5.9??? 氩+10%甲烷 0.21
2.6??? 0.31
α粒子 5.03??? 0.18
5.68??? 氩+0.8%甲烷 0.19
质子 1~4.5??? 硅 0.16
2.1.2 多次散射
带电粒子穿过物质时会被原子核和电子的库仑势散射(对于强子,强相互作
范文三:构成物质的基本粒子
课题:构成的物质的基本粒子
【学习目标】
1、知道物质是由分子、原子和离子构成的,能初步判断物质组成与构成能从宏观和微观的角度描述物质的
组成与构成;
2、理解分子、原子、离子概念及相互联系和区别,能解释自然界中的一些化学现象;
3、理解元素性质与原子结构的关系及元素与原子的区别与联系;了解原子结构与核外电子排布的初步知识。
自主复习
1、构成物质的粒子 、 、 。
2、分子是 ;
原子是 ;
离子是 。
3、分子和原子的区别是 ;联系是 。
4、原子是由 构成的,原子核通常是 构成的。
5、在元素周期表中,原子序数等于 。
6、在原子中, 数 == 数 == 数。
7、在离子中,离子的电荷数 == 数 — 数;在阳离子中,质子数== 数 + 数;在阴离子中,质子数 == 数 - 数。
8、相对原子质量 ≈ 数 + 数。
9、元素的种类是由 数或 数决定的,元素的化学性质主要是由原子结构中的 数决定的。
本节归纳:
请同学们归纳出我们学过的常见物质类别它们由哪种微粒构成:
原子:
分子:
离子:
合作探究
1`、如图所示,把充满红棕色二氧化氮气体和无色氢气的集气瓶中间玻璃片抽走,使两瓶口密合在一起(不
要振荡),可观察到A 中两瓶气体的颜色很快趋于一致(两者不反应),而B 中需要长时间才能达到同样的
效果。观察对比实验现象,由此可得到那些结论?
【巩固练习】
1、保持氢气化学性质的粒子是( )
A 、 H B 、 H 20 C 、 H 2 D 、 2H
2、有人通过闻茶的方法就能判断出茶的产地。人们能够闻到茶香的原因是( )
A .分子之间有间隔 B.分子在不断运动
C .分子的质量和体积都很小 D.分子是由原子构成的
3、下列结构示意图所表示的粒子属于稀有气体元素的是( )
4、下列原子结构示意图所表示的元素中,属于金属元素的是( )
1 / 2
5. 下列四种粒子的结构示意图中,说法正确的是( )
① ② ③ ④
A .它们表示四种不同的元素 B.②表示的元素在化合物中通常显+2价
C .①③④表示的元素都是非金属元素 D.①④表示的是阳离子
5、航天飞船常用铝粉与高氯酸铵(NH4ClO4)的混合物作为固体燃料,高氯酸铵中Cl 元素的化合价为( )
A .+1 B.+3 C.+5 D.+7
6、1996年科学家在宇宙深处发现了 H 3 + 离子和H 3分子。请回答:
(1)1个H 3 + 离子中含有 个质子 个电子;
(2)H 3分子的原子的结构示意图是 ;
(3)H 3属于 (填混合物或单质或化合物)。
7、(1)向容积为250 mL的细颈玻璃仪器A 中加水至虚线处,再滴几滴红墨水,一段
时间后,A 中的现象是_____________ ,说明______________ 。
(2)继续向A 中加酒精至凹液面最低处正好与刻度线相切。塞紧玻璃塞,将A 中液体
倒转摇匀,重复2次。静置一段时间后,A 中的现象为______________ ,说明
____________。仪器A 细颈部的作用是____________________。
8、(1)历史上,道尔顿认为,原子是一个个简单的、不可分割的实心球体。现在你认为该观点填“正确”或“错误”)。
(2)现代化学上,氧、铝两元素的原子结构示意图分别表示为:
下图是元素周期表的一部分(数字表示相应元素的原子序数),请用元素符号将两种元素填入表中相应位置。
(3)上表中硫元素的每个原子需要得到 个电子形成相对稳定结构的离子,该离子与Na +形成化合物的化学式为 。
(4)亚氯酸钠(NaClO2) 是一种重要的消毒剂,其中氯元素的化合价为。
2 / 2
范文四:金刚石的密度
2010-09-24 10:17:25|??分类: 合成石 |??标签: |字号大中小?订阅
金刚石的密度有差异,普通金刚石晶体,最大的密度等于3.51554g/cm3;最小等于3.514479/cm3;平均密度等于3.51539/cm3。H型金刚石密度波动比I型金刚石小。一颗完整H型金刚石晶体,它的晶格常数a=0.35668nm,根据晶格常数计算的密度ρx=3.515159/cm3,而用浮游法测量时,其测量值p0=3.515279/cm3。这里测的是普通、无色、质纯、结晶好的金刚石。但是,结构不一,杂质含量不同,其密度也各不相同。
黑金刚石的密度,由于其多孔和含煤与石墨的混合物,变化于3.012~3.416之间。金刚石晶体的密度与其颜色有一定关系:
金刚石的特征与密度的关系见表。
在论述金刚石颜色的性质时曾指出,烟色、褐色和浅玫瑰淡紫色是后成的,且与滑移面上的缺陷有关。可以预料,这种形式晶体的密度比无色的要低。从测量结果可以看出,浅褐色金刚石的密度与无色金刚石相当,而深褐色的则明显的降低。“和平”岩管的烟色金刚石和南非的浅玫瑰淡紫色晶体的密度更低,在晶体表面上清楚地呈现滑移线,密度3.51523g/cm3。
续表
颜色为绿色斑点的金刚石其密度稍低于无色金刚石。用辐射方法将两颗无色金刚石人工地染成绿色的金刚石,并测量了它们的密度。辐射照射后发现其密度也有所降低。
根据密度的平均值(3.51516g/cm3),发现黄色金刚石较无色和烟褐色的密度小。在黄色晶体中,颜色最强的密度最小。过去认为,金刚石的黄色是由杂质铁、铬和钛引起的。最近证实,这颜色是由取代碳原子的氮杂质引起的,它导致晶格常数增大,因而密度降低。
密度的精确测定,改正了过去所认为的黄色金刚石密度比无色金刚石高的结论。
染成黄绿色、浅绿色和深绿色的半透明和不透明的有壳金刚石的密度,比各种颜色的普通透明金刚石低。壳层本身的密度最小,它为3.50869g/cm3。显然晶体上的壳层越厚,它的密度便越低。
按颜色挑选,从无色到完全黑色的巴拉斯(球粒状)金刚石,它的密度随颜色强度作有规律的变化,即随杂质量(石墨)而变化,无色巴拉斯的密度为3.51515g/cm3;黑色的为3.50884g/cm3。卡邦纳达为金刚石的隐晶体3.0g/cm3。
人造金刚石密度,随触媒类型不同而异。就是同一种触媒合成出来的金刚石,由于压力、温度、时间等热动力学条件的改变,同样具有不同的色泽和不同的密度值。
金刚石是最硬的物质,同时也是比较脆并容易劈开的物质。在突然冲击下,某些金刚石晶体确实容易劈裂,这与一系列因素有关,如存在很大的内应力、裂缝和其他缺陷等。在存在很大应力的情况下,晶体甚至能沿滑移面自己劈开。完好的晶体经得住很大的静荷载。无外观缺陷的金刚石晶体被劈开的压力在30~100MPa之间。但是,具有裂缝和其他缺陷的晶体在低得多的负荷下就劈开了。而巴拉斯,尤其是卡邦纳达那样的金刚石,具有很大的韧性,很难劈开
范文五:金刚石的成因
金刚石的成因
地球形成以来巳有46亿年的历史。地球历史的地质时代划分为:太古宙(25亿年以前),元古宙(25亿年-5.7亿年),显生宙(5.7亿年-现今)。显生宙又划分为:古生代(5.7亿年-2.5亿年),中生代(2.5亿年-0.65亿年),新生代(0.65亿年-现今)。
下图显示了地球的内部结构,三个同心的层─地核、地幔和地壳,地核主要是铁─镍合金,巨大的地幔夹在地核和地壳之间,且聚集着大量的镁铁硅酸盐物质,地壳是一个很薄的岩石圈外壳。地球的岩石圈厚度为60-150km。岩石圈的上部是地壳,大陆地壳的厚度为30-80km,由沉积岩、花岗岩、玄武岩和各种变质岩组成。岩石圈的下部是上地幔,由橄榄岩组成。
各国金刚石地质学家对金刚石的成因巳进行了广泛深入的研究。目前认为金刚石是在大陆岩石圈的某些块段特定的地质构造环境中才能形成。虽然含有金刚石的寄主岩石有多种,例如在一些橄榄岩体和榴辉岩体中含有金刚石, 在西伯利亚的碱性-超基性杂岩、西澳的超基性和碱性煌斑岩、叙利亚的碧玄岩爆发岩筒、摩洛哥的石榴石辉石岩、哈萨克斯坦的片麻岩、中国西藏的方辉橄榄岩等岩石中都发现过金刚石,但具有经济价值的含金刚石的寄主母岩只有金伯利岩和钾镁煌斑岩。因此,金刚石的原生矿床也只有金伯利岩型和钾镁煌斑岩型两种,且以金伯利岩型为主。大陆岩石圈上有一些刚性的地块,在地质构造上具有双层结构,即由基底岩系和盖层岩系组成地壳。
基底岩系通常是太古宙或元古宙形成的极其古老的褶皱变质岩系,盖层是显生宙各个地质时代形成的相对年轻的产状平缓的沉积岩系。这种地块在大地构造单元中称为“地台”。
具有经济价值的含金刚石的金伯利岩体都是在古老的稳定的地台上发现的,如南非地台、安哥拉-开赛地台、印度地台、西伯利亚地台、西澳大利亚地台、北美地台、南美地台、中国的华北地台等。 这些古老地台的基底岩系都是太古宙或早元古代(17亿年以前)形成的。其中南非、安哥拉-开赛、西伯利亚和西澳大利亚4个地台区是目前世界上最主要的金刚石产区,共发现近1200个金伯利岩体,其中具有经济意义的含金刚石的金伯利岩筒约80个。
科学家们认为,金刚石是在地质构造上处于长期稳定状态的地台区岩石圈底部形成的。 这种地区岩石圈加厚而且相对较冷,具备金刚石结晶所需要的特定的温、压条件(见下图)。同时岩石圈底部的上地幔深部的正常热结构必须有一个“小的扰乱”(即偏离正常地温程度不大的温度升高),才能使地幔橄榄岩层发生低程度的局部熔融产生金伯利岩岩浆。这种“小的扰乱”不会破坏较冷岩石圈的热结构,不会将结晶出的金刚石相转变成石墨,可使金刚石在金伯利岩浆中保存下来并被岩浆带到地壳上部或近地表形成金伯利岩型金刚石矿床。
科学家们推测, 金刚石形成可能有3种途径:(1)太古宙的粗大钻石是长期地质作用的产物,(2)太古宙下沉的大洋地壳转变成榴辉岩在伴随的升温中形成与硫化物矿物共生的粗粒金刚石, (3)金伯利岩岩浆喷发前在岩石圈底部上升的C、H、O 等流体的作用下形成微粒金刚石。多数具有经济价值
的金刚石都是在上地幔形成的,所以这些金刚石是寄主金伯利岩岩浆上升过程中的捕虏晶。



 小小果99561791
小小果99561791

