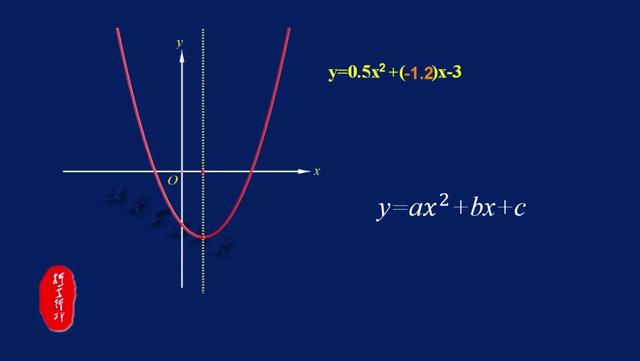
范文一:初中数学抛物线
初中数学抛物线
1、 左同右异:当抛物线y=ax2+bx+c(a≠0) 对称轴在Y 轴左侧时a
与b 同号;当对称轴在Y 轴右侧时a 与b 异号。
2、 左移加,右移减;上移加,下移减:当抛物线向左移动几个单
位时就在横坐标x 上加几个单位,当抛物线向右移动几个单位时就在横坐标x 上减几个单位。当抛物线向上移动几个单位时就在常数项c 上加几个单位,当抛物线向下移动几个单位时就在常数项c 上减几个单位。例如:y=3x2+2x-1向左移动2个单位,再向上移动5个单位后解析式为y=3(x+3)2+2(x+3)-1+5
3、 抛物线y=ax2+bx+c(a≠0) 与x 轴两交点间距离公式:∣AB ∣
=
?4ac ∣a ∣
范文二:初中数学抛物线题目
篇一:初中数学抛物线与几何专题训练及答案
全国各地中考试题压轴题精选讲座
抛物线与几何问题
【知识纵横】
抛物线的解析式有下列三种形式:1、一般式:y?ax2?bx?c(a?0);2、顶点式:y
=a(x—h) 2-,k;3、交点式:y=a(x—x 1)(x—x 2 ) ,这里x 1、x 2 是方程ax 2 +bx+c=0的两个实根。
解函数与几何的综合题, 善于求点的坐标,进而求出函数解析式是解题的基础;而充分发挥形的因素,数形互动,把证明与计算相结合是解题的关键。
【典型例题】
【例1】 (浙江杭州) 在直角坐标系xOy中,设点A(0,t),点Q(t,b)。平移二 次函数y??tx2的图象,得到的抛物线F满足两个条件:?顶点为Q;?与x轴相交于B,C两点(?OB?<?OC?),连结A,B。 (1)是否存在这样的抛物线F,
OA?OB?OC,请你作出判断,并说明理由;
1
(2)如果AQ?BC,且tan?ABO=对应的二次函数的解析式。
【思路点拨】(1)由关系式OA
【例2】(江苏常州)如图,抛物线y?x?4x与x轴分别相交于点B、O,
它的顶点为
2
2
2
3
,求抛物线F 2
?OB?OC来构建关于t、b的方程;(2)讨论
t的取值范围,来求抛物线F对应的二次函数的解析式。
A,连接AB,把AB所的直线沿y轴向上平移,使它经过原点O,得到直线l,设P是直线l上一动点.
(1)求点A的坐标;
(2)以点A、B、O、P为顶点的四边形中,有菱形、等 腰梯形、直角梯形,请分别直接写出这些特殊四边形的顶点P的坐标;
(3)设以点A、B、O、P为顶点的四边形的面积为S, 点P的横坐标为x,
当4??S?6?,求x的取值范围.
2
【思路点拨】(3)可求得直线l的函数关系式是y=-2x,所以应讨论?当点P在第二象限时,x<0、 ?当点P在第四象限是,x0这二种情况。
【例3】(浙江丽水)如图,在平面直角坐标系中,已知点A坐标为(2,4),直线x?2与x轴相交于点B,连结OA,抛物线y?x2从点O沿OA方向平移,与直线x?2交于点P,顶点M到A点时停止移动( (1)求线段OA所在直线的函数解析式; (2)设抛物线顶点M的横坐标为m,
?用m的代数式表示点P的坐标; ?当m为何值时,线段PB最短;
(3)当线段PB最短时,相应的抛物线上是否存在点Q,使?QMA的面积与?PMA的面积相等,若存在,请求出点Q的坐标;若不存在,请说明理由(
【思路点拨】(2)构建关于PB的二次函数,求此函数的最小值;(3)分当点Q落在直线OA的下方时、当点Q落在直线OA的上方时讨论。
【例4】(广东省深圳市)如图1,在平面直角坐标系中,二次函
数
与x轴交于A、B两点, y?ax2?bx?c(a?0)的图象的顶点为D点,与y轴交于C点,1
A点在原点的左侧,B点的坐标为(3,0),OB,OC ,
3
tan?ACO,(
3
(1)求这个二次函数的表达式(
(2)经过C、D两点的直线,与x轴交于点E,在该抛物线上是否存在这样的点F, 使以点A、C、E、F为顶点的四边形为平行四边形,若存在,请求出点F的坐标;若不存在,请说明理由(
(3)若平行于x轴的直线与该抛物线交于M、N两点,且以MN为直径的圆与x 轴相切,求该圆半径的长度(
(4)如图2,若点G(2,y)是该抛物线上一点,点P是直线AG下方的抛物线上 一动点,当点P运动到什么位置时,?APG的面积最大,求出此时P点的坐标和?APG的最大面积.
【思路点拨】(2)可先以A、C、E、F为顶点的四边形为平行四边形时,求F点的坐标,再代入抛物线的表达式检验。(3)讨论?当直线MN在x轴上方时、?当直线MN在x轴下方时二种情况。(4)构建S关于x的二次函数,求它的最大值。
【例5】(山东济南)已知:抛物线y?ax2?bx?c(a?0),顶点C (1,?3),与x
轴交
于A、B两点,A(?1,0)(
4
(1)求这条抛物线的解析式(
(2)如图,以AB为直径作圆,与抛物线交于点D,与抛物线对称轴交于点E,依次连接A、D、B、E,点P为线段AB上一个动点(P与A、B两点不重合),过点P作PM?AE于M, PN?DB于N,请判断
PMPN
是否为定值? 若是,请求出此定值;若不是,请说明理由( ?
BEAD
(3)在(2)的条件下,若点S是线段EP上一点,过点S作FG?EP ,FG分别与边(
PAEF
AE、BE相交于点F、G(F与A、E不重合,G与E、B不重合),请判断是否成 ?
PBEG立(若成立,请给出证明;若不成立,请说明理由(
PMAP
【思路点拨】(2)证?APM??ABE, ?
BEAB
PNPB
同理:(3)证PH=BH且?APM??PBH ?
ADAB再证?MEP??EGF可得。
【学力训练】
1、(广东梅州)如图所示,在梯形ABCD中,已知AB?
5
CD, AD?DB,AD=DC=CB,AB=4(以AB所在直线为x轴,过D且垂直于AB的直线为y轴建立平面直角坐标系(
(1)求?DAB的度数及A、D、C三点的坐标; (2)求过A、D、C三点的抛物线的解析式及其对称轴L(
(3)若P是抛物线的对称轴L上的点,那么使
?PDB为等腰三角形的点P有几个?(不必求点P
的坐标,只需说明理由)
2、(广东肇庆)已知点A(a,y1)、B(2a,y2)、C(3a,y3)都在抛物线y?5x2?12x上.
(1)求抛物线与x轴的交点坐标; (2)当a=1时,求?ABC的面积;
(3)是否存在含有y1、y2、y3,且与a无关的等式,如果存在,试给出一个,并加以证明;如果不存在,说明(来自:WwW.xltkwJ.cOm 小龙 文档 网:初中数学抛物线题目)理由.
3、(青海西宁)如图,已知半径为1的?O1与x轴交于A,B两点,OM为?O1的切线,切点为M,圆心O1的坐标为(2,二次函数y??x2?bx?c的图象经过A,B两0),点(
(1)求二次函数的解析式; (2)求切线OM的函数解析式;
(3)线段OM上是否存在一点P,使得以P,O,A为顶点的三角形与?OO1M相似(若存在,请求出所有符合条
6
件的点P的坐标;若不存在,请说明理由(
4、(辽宁12市)如图,在平面直角坐标系中,直线
y?与x轴交于点A,与y轴交于点C,抛
物线y?ax?
2
x?c(a?0)经过A,B,C三点( 3
(1)求过A,B,C三点抛物线的解析式并求出顶点F的坐标;
(2)在抛物线上是否存在点P,使?ABP为直角三角形,若存在,直接写出P点坐标;若不存在,请说明理由; (3)试探究在直线AC上是否存在一点M,使得?MBF的周长最小,若存在,求出M点的坐标;若不存在,请说明理由(
5、(四川资阳)如图,已知点A的坐标是(,1,0),点B的坐标是(9,0),以AB为直径作?O′,交y轴的负半轴于点C,连接AC、BC,过A、B、C三点作抛物线(
(1)求抛物线的解析式;
(2)点E是AC延长线上一点,?BCE的平分线CD交?O′于点D,连结BD,求直线BD的解析式;
(3)在(2)的条件下,抛物线上是否存在点P,使得?PDB,?CBD?如果存在,请求出点P的坐标;如果不存在,请说明理由(
x
7
篇二:中考数学抛物线压轴题
1. 如图1,抛物线C1:y=ax+bx+2与直线AB:y=x+交于x轴上的一点A,和另一点B(3,n)(
2
(1)求抛物线C1的解析式;
(2)点P是抛物线C1上的一个动点(点P在A,B两点之间,但不包括A,B两点),PM?AB于点M,PN?y轴交AB于点N,在点P的运动过程中,存在某一位置,使得?PMN的周长最大,求此时P点的坐标,并求?PMN周长的最大值;
(3)如图2,将抛物线C1绕顶点旋转180?后,再作适当平移得到抛物线C2,已知抛物线C2的顶点E在第四象限的抛物线C1上,且抛物线C2与抛物线C1交于点D,过D点作x轴的平行线交抛物线C2于点F,过E点作x轴的平行线交抛物线C1于点G,是否存在这样的抛物线C2,使得四边形DFEG为菱形,若存在,请求E点的横坐标;若不存在请说明理由(
2. (2013?桂林)已知抛物线的顶点为(0,4)且与x轴交于(,2,0),(2,0)(
(1)直接写出抛物线解析式;
(2)如图,将抛物线向右平移k个单位,设平移后抛物线的顶点为D,与x轴的交点为A、B,与原抛物线的交点
8
为P(
?当直线OD与以AB为直径的圆相切于E时,求此时k的值;
?是否存在这样的k值,使得点O、P、D三点恰好在同一条直线上,若存在,求出k值;若不存在,请说明理由(
3(如图,抛物线y=ax+bx+c与x轴交于点A、B,与y轴交于点C,OC=4,AO=2OC,且抛物线对称轴为直线x=,3(
(1)求该抛物线的函数表达式;
(2)己知矩形DEFG的一条边DE在线段AB上,顶点F、G分别在AC、BC上,设OD=m,矩形DEFG的面积为S,当矩形DEFG的面积S取最大值时,连接DF并延长至点M
,使
,求出此时点M的坐标;
(3)若点Q是抛物线上一点,且横坐标为,4,点P是y轴上一点,是否存在这样的点P,使得?BPQ是直角三角形,如果存在,求出点P的坐标;若不存在,请说明理由(
2
4(如图,抛物线y=ax+bx+c(a?0)与x轴交于A、B两点,其中A点坐标为(,1,0),线段AB=6,,M为抛物线的顶点( 2
9
(1)求抛物线的解析式;
(2)求?MCB的面积;
(3)若点D为线段BM上任一点(点D不与点B重合,可与点M重合),过点D作垂直于x轴的直线x=t,交抛物线于点E,交线段BC于点F(
?求当t为何值时,线段DE有最大值,最大值是多少,
?是否存在这样的点D,使得,若存在,求出D点的坐标;若不存在,则请说明理由(
5((2013?三明)如图,?ABC的顶点坐标分别为A(,6,0),B(4,0),C(0,8),把?ABC
2沿直线BC翻折,点A的对应点为D,抛物线y=ax,10ax+c经过点C,顶点M在直线BC
上(
(1)证明四边形ABCD是菱形,并求点D的坐标;
(2)求抛物线的对称轴和函数表达式;
(3)在抛物线上是否存在点P,使得?PBD与?PCD的面积相等,若存在,直接写出点P的坐标;若不存在,请说明理由(
6(如图,抛物线y=ax+bx,2经过A(4,0),B(1,0)两点(
(1)求出抛物线的解析式;
(2)若P是抛物线上x轴上方的一动点,过P作PM?x
10
轴,垂足为M,是否存在P点,使得以A,P,M为顶点的三角形与?OAC相似,若存在,请求出符合条件的点P的坐标;若不存在,请说明理由;
(3)在直线AC上方的抛物线上有一点D,使得?DCA的面积最大,求出点D的坐标(
2
7. (2011?历城区一模)已知:直角梯形OABC中,BC?OA,?AOC=90?,以AB为直径的圆M交OC于D、E,连接AD、BD、BE(
(1)在不添加其他字母和线的前提下,直接写出图1中的两对相似三角形(
_________ , _________ ;
(2)直角梯形OABC中,以O为坐标原点,A在x轴正半轴上建立直角坐标系(如图2),
2若抛物线y=ax,2ax,3a(a,0)经过点A、B、D,且B为抛物线的顶点(
?写出顶点B的坐标(用a的代数式表示) _________ ;
?求抛物线的解析式;
?在x轴下方的抛物线上是否存在这样的点P:过点P做PN?x轴于N,使得?PAN与?OAD相似,若存在,求出点P的坐标;若不存在,说明理由(
8((2008?崇安区二模)已知,如图,抛物线y=x+px+q
11
与x轴相交于A、B两点,与y轴交于点C,且OA?OB,OA=OC,设抛物线的顶点为点P,直线PC与x轴的交点D恰好与点A关于y轴对称(
(1)求p、q的值(
(2)在题中的抛物线上是否存在这样的点Q,使得四边形PAQD恰好为平行四边形,若存在,求出点Q的坐标;若不存在,请说明理由(
(3)连接PA、AC(问:在直线PC上,是否存在这样点E(不与点C重合),使得以P、
A、E为顶点的三角形与?PAC相似,若存在,求出点E的坐标;若不存在,请说明理由(
2
9((2012?衢州模拟)如图,已知抛物线y=ax+bx+c与x轴交于A、B两点,与y轴交于点C,D为OC的中点,直线AD交抛物线于点E(2,6),且?ABE与?ABC的面积之比为3:2(
(1)求这条抛物线对应的函数关系式;
(2)连接BD,试判断BD与AD的位置关系,并说明理由;
(3)连接BC交直线AD于点M,在直线AD上,是否存在这样的点N(不与点M重合),使得以A、B、N为顶点的三角形与?ABM相似,若存在,请求出点N的坐标;
12
若不存在,请说明理由(
2
篇三:初三数学抛物线练习试题
初三数学抛物线练习试题
学校:___________姓名:___________班级:___________考号:___________
一、选择题(题型注释)
1(教室的饮水机接通电源就进入自动程序,开机加热时每分钟上升10?,加热到100?后停止加热。水温开始下降,此时水温y(?)与开机后用时x(min)成反比例关系。直到水温降至20?,饮水机关机。饮水机关机后即刻自动开机。重复上述自动程序,若在水温为20?时,接通电源后,水温y(?)和时间x(min)的关系如图所示,为了在上午第一节课下课时(8:45)能喝到不超过40?的水,则接通电源的时间可以是当天上午的( )
A(7:10 B(7:20 C(7:30 D(7:50
2(若mn,0,则一次函数( )
与反比例函数在同一坐标系中的大致图象是
3(已知下列命题,其中真命题的个数是( ) ?若,则;
?对角线互相垂直平分的四边形是菱形;
?两组对角分别相等的四边形是平行四边形; ?在反比例函数
13
A(4个
4(函数中,如果函数值y1时,那么自变量x2( B(3个 C(2个 D(1个 的自变量x的取值范围在数轴上表示为()
二、填空题(题型注释)
5(如图,四边形是矩形,四边形是正方形,点在轴的负半轴上,点在轴的正半轴上,点的面积为4,且在上,点在反比例函数
的图像上,正方形,则值为____(
6(已知点(、(、(在双曲线上,那么、
、的大小关系是_(
三、解答题(题型注释)
7((10分)某公司经营一种绿茶,每千克成本为50元(市场调查发现,在一段时间内,销售量w(千克)随销售单价x(元/千克)的变化而变化,具体关系式为:w,,2x,240.设这种绿茶在这段时间的销售利润为y(元),解答下列问题:
(1)求y与x的关系式
(2)当x取何值时,销售利润最大,最大利润是多少,
8((8分)拱桥的形状是抛物线,其函数关系式为m时,水面的宽度为多少米,
,当水面离桥顶的高度为
9(2008年6月1日起,我国实施“限塑令”,开始有偿
14
使用环保购物袋. 为了满足市场需求,某厂家生产A、B两种款式的布质环保购物袋,每天共生产4500个,两种购物袋的成本和售价如下表,设每天生产A种购物袋x个,每天共获利y元.
(1)求出y与x的函数关系式;
(2)如果该厂每天最多投入成本10000元,那么每天最多获利多少元,
10(如图,已知直线与双曲线交于、两点,点横坐标为4(
(1)求值;
(2)直接写出关于的不等式的解集;
(3)若双曲线(4)若在轴上有点形,直接写出点、上有一点,轴上有点的坐标( 的纵坐标为8,求?,且点、、、的面积( 四点恰好构成平行四边11(某生态示范村种植基地计划用90亩,120亩的土地种植一批葡萄,原计划总产量要达到36万斤(
(1)列出原计划种植亩数(亩)与平均每亩产量(万斤)之间的函数关系式,并写出自变量的取值范围;(总产量=亩数平均每亩产量)
(2)为了满足市场需求,现决定改良葡萄品种(改良后平均每亩产量是原计划的1(5倍,总产量比原计划增加了8万斤,种植亩数减少了20亩,原计划和改良后的平均每亩产量各是多少万斤,
15
12(如图,抛物线经过点A(4,0)、B(1,0)、C(0,,
2)三点(求此抛物线的解析式;
16
范文三:初中数学抛物线教案
精品文档
初中数学抛物线教案
教学目标:
能够根据实际问题,熟练地列出二次函数关系式,并求出函数的自变量的取值范围。
注重学生参与,联系实际,丰富学生的感性认识,培养学生的良好的学习习惯
重点难点:
能够根据实际问题,熟练地列出二次函数关系式,并求出函数的自变量的取值范围。
教学过程:
一、试一试
1.设矩形花圃的垂直于墙的一边AB的长为xm,先取x的一些值,算出矩形
的另一边BC
2(x的值是否可以任意取?有限定范围吗?
3(我们发现,当AB的长确定后,矩形的面积也随之确定, y是x的函数,试写出这个函数的关系式,
对于1.,可让学生根据表中给出的AB的长,填出相应的BC的长和面积,然后引导学生观察表格中数据的变化情况,提出问题:从所填表格中,你能发现什么,对前面提出的问题的解答能作出什么猜想?让学生思考、交流、发表意见,达成共识:当AB的长为5cm,BC的长为10m时,围
1 / 20
精品文档
成的矩形面积最大;最大面积为50m2。
对于2,可让学生分组讨论、交流,然后各组派代表发表意见。形成共识,x的值不可以任意取,有限定范围,其范围是0 ,x ,10。
对于3,教师可提出问题,当AB=xm时,BC长等于多少m?面积y等于多少?并指出y=x就是所求的函数关系式(
二、提出问题
某商店将每件进价为8元的某种商品按每件10元出售,一天可销出约100
件(该店想通过降低售价、增加销售量的办法来提高利润,经过市场调查,发现这种商品单价每降低0.1元,其销售量可增加10件。将这种商品的售价降低多少时,能使销售利润最大?
在这个问题中,可提出如下问题供学生思考并回答: 1(商品的利润与售价、进价以及销售量之间有什么关系? [利润=×销售量]
2(如果不降低售价,该商品每件利润是多少元?一天总的利润是多少元? [10,8=2,×100=200]
3(若每件商品降价x元,则每件商品的利润是多少元?一天可销售约多少件商品?
[;]
4(x的值是否可以任意取?如果不能任意取,请求出
2 / 20
精品文档
它的范围, [x的值不能任意取,其范围是0?x?2]
5(若设该商品每天的利润为y元,求y与x的函数关系式。 [y= ]
将函数关系式y=x??????????? 将函数关系式y=化为: y=,100x2,100x,20D ???????? 三、观察;概括
1.教师引导学生观察函数关系式和,提出以下问题让学生思考回答; 函数关系式和的自变量各有几个?
多项式,2x2,20和,100x2,100x,200分别是几次多项式?
函数关系式和有什么共同特点?
本章导图中的问题以及P1页的问题2有什么共同特点,
让学生讨论、交流,发表意见,归结为:自变量x为何值时,函数y取得最大值。
2(二次函数定义:形如y=ax2,bx,c 的函数叫做x的二次函数,a叫做二次函数的系数,b叫做一次项的系数,c叫作常数项( 四、课堂练习
1.下列函数中,哪些是二次函数? y=5x,1 y=4x2,1
y=2x3,3xy=5x4,3x,1 (P3练习第1,2题。
五、小结
1(请叙述二次函数的定义(
3 / 20
精品文档
2,许多实际问题可以转化为二次函数来解决,请你联系生活实际,编一道二次函数应用题,并写出函数关系式。
六、作业:略
6. 二次函数的图象与性质
[教学目标]
会用描点法画出二次函数y?ax2的图象,概括出图象的特点及函数的性质( [教学过程] [新课引入]
我们已经知道,一次函数
y?2x?1,反比例函数
2
y?
3
x的图象分别
是 、 ,那么二次函数y?x的图象是什么呢,
2
y?x描点法画函数的图象前,想一想,列表时如何合理选值,以什么数
为中心,当x取互为相反数的值时,y的值如何,
2y?x观察函数的图象,你能得出什么结论,
[例题精讲]
例1(在同一直角坐标系中,画出下列函数的图象,并指出它们有何共同点,有何不同点,
4 / 20
精品文档
y?2xy??2x2
分别描点、连线,画出这两个函数的图象,这两个函数的图象都是抛物线,如图26(2(1(
共同点:都以y轴为对称轴,顶点都在坐标原点(
不同点:y?2x的图象开口向上,顶点是抛物线的最低点,在对称轴的左边,
曲线自左向右下降;在对称轴的右边,曲线自左向右上升(
2
y??2x2的图象开口向下,顶点是抛物线的最高点,在对称轴的左边,
曲线自左向右上升;在对称轴的右边,曲线自左向右下降(
回顾与反思 在列表、描点时,要注意合理灵活地取值以及图形的对称性,因为图象是抛物线,因此,要用平滑曲线按自变量从小到大或从大到小的顺序连接( 例2(已知y?xk
2
?k?4
是二次函数,且当x?0时,y随x的增大而增大(
求k的值;
求顶点坐标和对称轴(
5 / 20
精品文档
?k2?k?4?2
解 由题意,得?, 解得k=2(
?k?2?0
二次函数为y?4x2,则顶点坐标为,对称轴为y轴( 例3(已知正方形周长为Ccm,面积为S cm2( 求S和C之间的函数关系式,并画出图象; 根据图象,求出S=1 cm2时,正方形的周长; 根据图象,求出C取何值时,S?cm2(
分析 此题是二次函数实际应用问题,解这类问题时要注意自变量的取值范围;画图象时,自变量C的取值应在取值范围内( 解 由题意,得S
?
12
C(
16
描点、连线,图象如图26(2(2(
根据图象得S=1 cm2时,正方形的周长是4cm( 根据图象得,当C?8cm时,S?cm2( 回顾与反思
此图象原点处为空心点(
横轴、纵轴字母应为题中的字母C、S,不要习惯地写成x、y( 在自变量取值范围内,图象为抛物线的一部分( [当堂课内练习]
1(在同一直角坐标系中,画出下列函数的图象,并
6 / 20
精品文档
分别写出它们的开口方向、对称轴和顶点坐标(
y?3xy??3xy?2(函数y?
12
x
22
x的开口,对称轴是,顶点坐标是;
12
函数y??x的开口,对称轴是,顶点坐标
4
是(
3(已知等边三角形的边长为2x,请将此三角形的面积S表示成x的函数,并画出图象的草图(
6( 二次函数的图象与性质
[教学目标] 会画出y?ax2[教学过程] [例题精讲]
例1(在同一直角坐标系中,画出函数y?2x2与y?2x2
?k这类函数的图象,通过比较,了解这类函数的性质(
?2的图象(
描点、连线,画出这两个函数的图象,如图26(2(3所示(
抛物线教案
数科院 王东帅 06090102
教学目标
7 / 20
精品文档
1 知识与能力目标:让学生掌握抛物线的基本知识和学会对于知识的应用,更好的理解圆锥曲线的通性,学会研究抛物线的基本方法,为以后的学习做准备。
过程与方法目标:在学习的过程中,让学生了解有关于类比推理的思想方法,在以后的学习中能够加以应用。
情感态度和价值观:感受事物变化联系的特点,初步认识事物的内在联系与统一。
教学难点
1 抛物线的定义
抛物线的四种基本方程
抛物线性质的应用
教学方法
1 演绎法:使用PPT展示相关的知识 ,在黑板上板书主要的内容。 反馈法:在讲解完知识后,让学生做相关的例题和变式题,有问题的当堂讲解,当堂反馈。
教学时间:45分钟。
教学对象:全体学生
教学形式:讲授,互动
教学流程:
1 课前导入:由生活中的实例,如拱桥,篮球轨迹,导入本节课的教学内容——抛物线
知识回顾:回顾前几次课有关于椭圆和双曲线的基本
8 / 20
精品文档
知识,为了学习抛物线有关知识做准备,有利于学生对于知识的把握和理解。 知识讲解:通过类比推理,讲解抛物线的相关知识,如定义,方程,性质等。
反馈巩固:带领学生做与抛物线基本知识相对应的例题,然后由学生自己做变式题,最后我进行疑难解答。
布置作业,让同学在课后更好的学习和巩固相关知识。 附板书设计
抛物线
初中数学二次函数复习专题
〖知识点〗二次函数、抛物线的顶点、对称轴和开口方向 〖大纲要求〗
1( 理解二次函数的概念;
2( 会把二次函数的一般式化为顶点式,确定图象的顶点坐标、对称轴和开口方向,会
用描点法画二次函数的图象;
3( 会平移二次函数y,ax2的图象得到二次函数y,a2,k的图象,了解特殊与一般相互联系和转化的思想;
4( 会用待定系数法求二次函数的解析式;
5( 利用二次函数的图象,了解二次函数的增减性,会求二次函数的图象与x轴的交点
坐标和函数的最大值、最小值,了解二次函数与一元二次方程和不等式之间的联系。
9 / 20
精品文档
内容
二次函数及其图象
如果y=ax2+bx+c,那么,y叫做x的二次函数。 二次函数的图象是抛物线,可用描点法画出二次函数的图象。 抛物线的顶点、对称轴和开口方向 抛物线y=ax+bx+c的顶点是,对称轴是x??
b2a
,当a>0时,
抛物线开口向上,当a 1( 考查二次函数的定义、性质,有关试题常出现在选择题中,如: 已知以x为自变量的二次函数y,x2,m2,m,2额图像经过原点,
则m的值是
2( 综合考查正比例、反比例、一次函数、二次函数的图像,习题的特点是在同一直角
坐标系内考查两个函数的图像,试题类型为选择题,如:
如图,如果函数y,kx,b的图像在第一、二、三象限内,那么函数 y,kx2,bx,1的图像大致是
3( 考查用待定系数法求二次函数的解析式,有关习题出现的频率很高,习题类型有中
档解答题和选拔性的综合题,如:
已知一条抛物线经过,两点,对称轴为x, ,求这条
10 / 20
精品文档
抛物线的解析式。
3
4( 考查用配方法求抛物线的顶点坐标、对称轴、二次函数的极值,有关试题为解答题,
如:
已知抛物线y,ax,bx,c与x轴的两个交点的横坐标是,1、3,与y轴交点的纵坐3
标是, 确定抛物线的解析式;用配方法确定抛物线的开口方向、对称轴和顶点坐
2标.
5(考查代数与几何的综合能力,常见的作为专项压轴题。
习题1:
一、填空题:
,、已知,在第一象限,则点,在第 象限 ,
,、对于,,, ,当,,,时,,随,的增大而
,
,、二次函数,,,,,,,,取最小值是,自变量,的值是
,
,、抛物线,,,,的对称轴是直线,, ,、直线,,,,,,,在,轴上的截距是
11 / 20
精品文档
,
,、函数,, 中,自变量,的取值范围是
,,,,
,、若函数,,,,,,,,,,是反比例函数,则m的值为,、在公式
,,,
,,中,如果,是已知数,则,,
,,,
2
,、已知关于,的一次函数,,,,,,如果,随,的增大而减小,则,的取值
范围是
,,、 某乡粮食总产值为,吨,那么该乡每人平均拥有粮食,,与该乡人口数,的函
数关系式是 二、选择题:
,,、函数,, 中,自变量,的取值范围
,,, ,,, ,?,,?, ,,、抛物线,,,,,的顶点在
第一象限 第二象限 第三象限 第四象限 ,,、抛物线,,与坐标轴交点的个数为 ,, , ,
,,、下列各图中能表示函数和在同一坐标系中的图象大致是
12 / 20
精品文档
15(平面三角坐标系内与点关于,轴对称点的坐标为
1
16(下列抛物线,对称轴是直线,, 的是
2
12222
,,,,,,,2,,,,,,,2,,,,,,2
23,
17(函数,,中,,的取值范围是
1,2,
111
,?0 ,,,? ,,222
18(已知A,B两点,则经过A、B两点的直线是31
,,, ,,, ,,3, ,, ,,1
323
19(不论,为何实数,直线,,,,2,与,,,,,的交点不可能在
第一象限 第二象限 第三象限 第四象限0(某幢建筑物,从10米高的窗口A用水管和向外喷水,喷的水流呈抛物线如果抛物线的最高点M离墙1米,米,
3则水流下落点B离墙距离OB是
2米3米4米5米
13 / 20
精品文档
三(解答下列各题
1
21(已知:直线,,,,,过点A。求,的值;判断点B
2是否在这条直线上;指出这条直线不过哪个象限。
522(已知抛物线经过A,B两点,对称轴为,, ,
3
求这条抛物线的解析式;
试证明这条抛物线与X轴的两个交点中,必有一点C,使得对于,轴上任意一点D都
有AC,BC?AD,BD。
23(已知:金属棒的长1是温度,的一次函数,现有一根金属棒,在O?时长度为200;,,温度提高1?,它就伸长0.002;,。
求这根金属棒长度,与温度,的函数关系式; 当温度为100?时,求这根金属棒的长度;
当这根金属棒加热后长度伸长到201.6;,时,求这时金属棒的温度。
24(已知,1,,2,是关于,的方程,,3,,,,0的两个不同的实数根,设,,,1,, 求S关于,的解析式;并求,的取值范围;
当函数值,,7时,求,13,8,2的值;
14 / 20
精品文档
25(已知抛物线,,,2,,,9顶点在坐标轴上,求,的值。
,,、如图,在直角梯形,,,,中,?,,?,,,,?,截取,,,,,,,,,,,已知,,,,,,,,,,,,,,,求:
四边形,,,,的面积,关于,的函数表达式和,的取值范围; 当,为何值时,,的数值是,的,倍。
2
2
2
D
XGC
EXA
F
XB
,,、国家对某种产品的税收标准原定每销售,,,元需缴税,元,台洲经济开发区某工厂计划销售这种产品,吨,每吨,,,,元。国家为了减轻工人负担,将税收调整为每,,,元缴税元,),这样工厂扩大了生产,实际销售比原计划增加,,,。
写出调整后税款,与,的函数关系式,指出,的取值范围;
15 / 20
精品文档
要使调整后税款等于原计划税款的,,,,求,的值( ,,、已知抛物线,,,,,,,,,与,轴的交点为,,与,轴的交点为,,,
写出,,,,,三点的坐标;
设,,,,,,,,,试问是否存在实数,,使?,,,为,,?,若存在,求出,的
值,若不存在,请说明理由; 设,,,,,,,,,当?,,,最大时,求实数,的值。 习题2:
一(填空
3
1(二次函数=2+1图象的对称轴是 。
22(函数
,
。
3(若一次函数y=x+m+1的图象过一、二、四象限,则的取值范围是。(已知关于的二次函数图象顶点,且图象过点,则这个二次函数解析式为。
5(若y与x成反比例,位于第四象限的一点P在这个函数图象上,且a,b是方程x-x -12=0的两根,则这个函数的关系式 。(已知点P在反比例函数y=这个函数图象在第象限。( x,y满足等式x=是。
8(二次函数y=ax+bx+c+的图象如图,则点P
16 / 20
精品文档
2
2
2
kx
的图象上,其中a=m2+2m+3,则
3y?22y?1
,把y写成x的函数,其中自变量xy
-2
o
x
在坐标系中位于第 象限 -2
9(二次函数y=2+2,当x= 时,达到最小值 。 10(抛物线y=x2-x-m与x轴交于和两点,已知x1x2=x1+x2+49,
要使抛物线经过原点,应将它向右平移个单位。 二(选择题
11(抛物线y=x2+6x+8与y轴交点坐标
12(抛物线y= -12
2+3的顶点坐标
13
y=kx2+bx-1的图象大致是
14(函数y=
17 / 20
精品文档
x?1
y
B
y1
-1x
Cox
D-1
oxy
o
x )
x?x -且x?1 x?2且x?–1
15(把抛物线y=3x2先向上平移2个单位,再向右平移3个单位,所得抛物线的解析式是
22
=3- =3+2=3-2=3+16(已知抛物线=x+2mx+m -7与x轴的两个交点在点两旁,则关于x的方程x+m+5=0的根的情况是
有两个正根 有两个负数根有一正根和一个负根 无实根 17(函数y= - x的图象与图象y=x+1的交点在
第一象限 第二象限 第三象限 第四象限 18(如果以y轴为对称轴的抛物线y=ax+bx+c的图象,如图, 则代数式b+c-a与0的关系
18 / 20
精品文档
b+c-a=0 b+c-a>0 b+c-a 2
y
2
14
x+
2
2
Ox
x +6和y=x -,它们与y轴所围成的三角形的面积为
6102012
20(某学生从家里去学校,开始时匀速跑步前进,跑累了后,再匀速步行余下的路程。下图所示图中,横轴表示该生从家里出发的时间t,纵轴表示离学校的路程s,则路程s与时间t )
s
sss
oA
2
to
B
t
o
19 / 20
精品文档
C
t
o
D
t
三(解答题
21(已知抛物线y=ax+bx+c与x轴的两交点的横坐标分别是-1和3,与y轴交点的纵坐标是-32
;
20 / 20
范文四:初中数学抛物线专项练习
5、(2009年滨州)某商品的进价为每件40元.当售价为每件60元时,每星期可卖出300件,现需降价处理,且经市场调查:每降价1元,每星期可多卖出20件.在确保盈利的前提下,解答下列问题:
(1)若设每件降价x 元、每星期售出商品的利润为y 元,请写出y 与x 的函数关系式,并求出自变量x 的取值范围;
(2)当降价多少元时,每星期的利润最大?最大利润是多少?
如图,在平面直角坐标系中,OB ⊥OA ,且OB =2OA ,点A 的坐
标是(-1,2) .
(1)求点B 的坐标;
(2)求过点A 、O 、B 的抛物线的表达式;
(3)连接AB ,在(2)中的抛物线上求出点P ,使得S △ABP
=S △ABO .
如图,已知抛物线与x 交于A(-1,0) 、E(3,0) 两点,与y
(1) 求抛物线的解析式;
(2) 设抛物线顶点为D ,求四边形AEDB 的面积;
(3) △AOB 与△DBE
如图12,已知抛物线y =x +4x +3交x 轴于A 、B 两点,交y 轴交x 轴于点E ,点B 的坐标为(-1,0).
(1)求抛物线的对称轴及点A 的坐标;
(2)在平面直角坐标系xoy 中是否存在点P ,
与A 、B 、C 三点构成一个平行四边形?若存在,
请写出点P 的坐标;若不存在,请说明理由;
(3)连结CA 与抛物线的对称轴交于点D ,在抛物线上是否存在
点M ,使得直线CM 把四边形DEOC 分成面积相等的两部分?
若存在,请求出直线CM 的解析式;若不存在,请说明理由.
图2
范文五:初中数学抛物线压轴题举例
1. 已知抛物线y 1=x 2-2x +c 的部分图象如图1所示.
图1 图2
(1)求c 的取值范围;
(2)若抛物线经过点(0,-1),试确定抛物线y 1=x 2-2x +c 的解析式;
(3)若反比例函数y 2=k x 的图象经过(2)中抛物线上点(1,a ),试在图2所示直角坐标系中,画出该反比例函数及(2)中抛物线的图象,并利用图象比较y 1与y 2的大小.
2. 如图1,已知直线y =-1
2x 与抛物线y =-1
4x +6交于A ,B 两点. 2
(1)求A ,B 两点的坐标;
(2)求线段A B 的垂直平分线的解析式;
(3)如图2,取与线段A B 等长的一根橡皮筋,端点分别固定在A ,B 两处.用铅笔拉着这根橡皮筋使笔尖P 在直线A B 上方的抛物线上移动,动点P 将与A ,B 构成无数个三角形,这些三角形中是否存在一个面积最大的三角形?如果存在,求出最大面积,并指出此时P 点的坐标;如果不存在,请简要说明理由.
图1
图2



 兔族看门老王
兔族看门老王

