范文一:近自由电子近似理论
近自由电子近似理论
这是能带理论中一个简单模型。该模型的基本出发点是晶体中的价电子行为很接近于自由电子,周期势场的作用可以看作是很弱的周期性起伏的微扰处理。仅管模型简单,但给出了周期场中运动的电子本征态的一些最基本特点。
5.3.1模型与零级近似
这个模型的基本思想是:模型认为金属中价电子在一个很弱的周期场中运动(如图5-3-1),价电子的行为很接近于自由电子,又与自由电子不同。这里的弱周期场设为?V(x) ,可以当作微扰来处理,即: (1)零级近似时,用势场平均值代替弱周期场V(x);
(2)所谓弱周期场是指比较小的周期起伏[V(x)-V]=?V(x)做为微扰处理。
为简单起见,我们讨论一维情况。
V(r)
图5-3-1 单电子的周期性势场
零级近似下,电子只受到V作用,波动方程及电子波函数,电子能量分别为:
d20000-ψ+Vψ=Eψ22mdx
ikx
ψk0(x)=……………………………………(5-3-1)
2k20
Ek=+V
2m
由于晶体不是无限长而是有限长L,因此波数k不能任意取值。当引入周期性边界条件,则k只能取下列值:k=
2π
l,这里l为整数 Na
可见,零级近似的解为自由电子解的形式,故称为近自由电子近似理论。
5.3.1微扰计算
根据量子力学的微扰理论,可以知道:
零级近似
微扰理论重要公式
能量本征值 一级修正 二级修正
零级近似
2k2
E=+V
2m
Ek(1)=k?Vk
0k
Ek(2)=∑'
k'
k'?VkEk0-Ek0'
2
ψk0(x)=
电子波函数
一级修正
ikx
k'?VkE-E
0k
0k'
ψk(1)(x)=∑'
k'
k0'(x5-3-2) 5-3-3)
5-3-4)
5-3-5)
5-3-6)
首先计算能量的一级修正:
因此有能量的一级修正为零,必须根据(5-3-4)计算二级修正: 因为k'?Vk=k'(x)-Vk=k'(x)k=代入波函数表达式并按原胞划分,可得:
1L-i(k'-k)x1N-1(n+1)a-i(k'-k)x
k'?Vk=?eV(x)dx=eV(x)dx…………………………………(5-3-9)∑?0naLNa0
这里令x=ξ+na,则V(x)=V(ξ+na)=V(ξ),因此有:
1N-1-i(k'-k)naa-i(k'-k)ξ
k'?Vk=k'V(x)k=eeV(ξ)dξ……………………………………(5-3-10)∑?0Na0?1a-i(k'-k)ξ?1
整理上式为:k'?Vk=??eV(ξ)dξ?
?a0?N
下面分为两种情况讨论:
12π
(1)当k'-k=n?时,有
Na
所以二级修正为:Ek
(2)
(2)k'-k≠n?
所以,在周期势场的情况下,计入能量的二级修正后晶体中电子的能量本征值为:
E
(1)
k
=k?Vk=?ψ?Vψdx=?ψk0*[V(x)-V]ψk0dx
0*
k0k
L
=?ψV(x)ψdx-?ψk0*Vk0dx=V-V=0…………………………………………(5-3-7)
L
0*
k0k
L
?
L
ψk0*ψk0dx……………………………(5-3-8) 'V(x)
∑(e
N-1
-i(k'-k)an
)………………………………(5-3-11)
∑(e
00
k
N-1
-i(k'-k)an
?1a-in?2aπξ?
V(ξ)dξ?=Vn )=1,则设k'?Vk=??e
0?a?
n
2
2
=∑'
k'
k'?VkE-E
k'
2
=∑'
k'
2πn2
[k2-(k+)]2ma
-i(k'-k)Na
……………………………(5-3-12)
12π
时,有
Na
∑(e-i(k'-k)a)n=
N-1
11-e(2)'
=0,则有E=∑kN1-e-i(k-k)ak'
k'?VkE-E
k
0k'
2
=0
Ek=Ek(0)+Ek(1)+Ek(2)
n 2k2'
=+∑2……………………………(5-3-13)
2πn2mk'
[k2-(k+)2]2ma
2
5.3.3 重要结论 1、能带与禁带
在零级近似中,电子作为自由电子,其能量本征值Ek与k的关系曲线是抛物线,在周期势场的微扰下,Ek曲线在k=±
nπ
处断开,能量突变值为2n,如图5-3-2所示。在诸能带断开的间隔内不存在允a
l2π
而言,N很大,故k很密集,可以认为En(k)是k的准连续函数,这?Na
许的电子能级,称为禁带,禁带的位置及宽度取决于晶体的结构和势场的函数形式。
另一方面,对于波矢k=
些准连续的能级被禁带隔开而形成一系列能带1,2,3…。不难算出,每个能带所对应的k的取值范围都是2π/a,即一个倒格子原胞长度,而所包含的量子态数目是N,等于晶体中原胞的数目。
En(k)总体称为能带结构(n为能带编号),相邻两个能带En(k)与En+1(k)之间可以相接,重叠或是
分开,对于一维周期性势场来说属于分开情况,则出现带隙——禁带。
图5-3-2 近自由电子近似能带图示
2、能带的图示
从能量角度来看,可以将标志电子状态的波矢k分割成许多区域,在每个区域内电子能级E(k)随波矢k准连续变化并形成一个能带。波矢k的这样一些区域即为布里渊区。
根据图5-3-2,对应第一能带的k的取值范围称第一布里渊区或简约布里渊区,同理,对应第n个能带的k的取值范围则称为第n布里渊区。
函数En(k)与k的关系图称为能带表示图示,一般有三种不同的表示。
(1)简约布里渊区图示
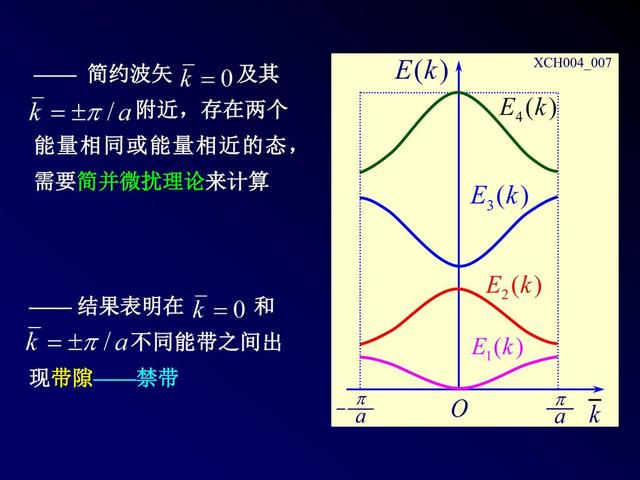
在这种表示中,k为简约波矢,即k限制在第一布里渊区内。E(k)是k的多值函数,为区分,将其按能量由低到高标记为E1(k),E2(k)…,图5-3-3为一维情况。这种图示的特点是在简约布里渊区表示出所有能带,可以看到能带结构的全貌,E(k)是k的多值函数,通常都采用这种图示。 (2)重复区图示
第一布里渊区的每个能带在整个k空间周期性重复,如图5-3-4所示。其特点:每个布里渊区都表示出所有的能带,E(k)是k的周期函数。 (3)扩展区图示
按能量由低到高的顺序,分别将能带k限制在第一布里渊区、第二布里渊区,…等等。一个布里渊区表示一个能带,如图(5-3-5)所示。其特点是:E(k)是k的单值函数,一个布里渊区表示一个能带。
图5-3-4 一维能带结构重复区图示
图5-3-5 一维能带结构扩展区图示
5.3.4 三维情况推广
三维晶格的情况可以用完全类似的方法进行讨论,这里只将一维情况推广到三维情况,给出必要的结果。 1、波动方程
? 22?-?+V(r)?2m?ψ(r)=Eψ(r)………………………………………………………………(5-3-14) ??
其中V(r)=V(r+Rm),而Rm=m1a1+m2a2+m3a3。 2、零级近似
0ψk(r)=
ik?r
…………………………………………………………………………………(5-3-15) 2k2
E=+V……………………………………………………………………………………(5-3-16)
2m
0k
其中k在周期性边界条件下取分立的值:
k=
ll1l
b1+2b2+3b3,…………………………………………………………………(5-3-17) N1N2N3
而-Ni/2≤li≤Ni/2(i=1,2,3)………………………………………………………………(5-3-18) 3、微扰计算
ψ
(1)k
=∑
k'
'
k'?VkE-E
0k
0k'
0k' ……………………………………………………………………(5-3-19)
Ek(1)=k?Vk=0……………………………………………………………………………(5-3-20)
E
(2)
k
=∑
k'
'
k'?Vk
00Ek-Ek'
2
…………………………………………………………………(5-3-21)
式中求和号上的撇表示不包括k'≠k的项。而k'?Vk则为:
?Vn(k'-k=Gn)
k'?Vk=? ……………………………………………………………(5-3-22)
'0(k-k≠G)?n
4、简并微扰
和一维情况类似,对于状态k和k'=k+Gn,其零级能量相等,ψk和Ek趋于∞,导致结果的发散。
(1)
(2)
2 2 1
这时的条件可具体写为:k=k+Gn或Gn?(k+Gn)=0
2
式(5-3-22)的几何意义是:在k空间从原点出发所作的倒格矢Gn的垂直平分面的方程,即在倒格矢垂直平分面上及其附近的k,应采用简并微扰理论(这里简并微扰计算从略),其计算结论同一维情况,即能带函数En(k)是在布里渊区边界处断开,发生能量突变,突变值为2n。
范文二:71 近自由电子模型
固体物理导论 第 7 章 能带 7.1 近自由电子模型 近自由电子近似 单电子近似
下,晶体电子的薛定谔方程 2 2 H V r E 2mV r 为电子所处的周期性势场,满足 V
r Rl V r V r 随空间位置的变化不太强烈时,可把 V r 的空间起伏看作是对自
由电子情形的微扰,这种假设称为近自由电子近似 1 固体物理导论 第 7 章 能带
7.1 近自由电子模型 7.1. 1 一维周期势的微扰计算 在一维情况下,电子的薛定谔方
程及周期势 2 d2 2 V x x E x 2 m dx V x la V x a 晶格常量,l 任意整数由
于 Vx 是周期函数,可以展开成傅里叶级数 2π 2π V x Vn e V0 Vn e in x in x a a n
n0 平均势场,可令 V00 2固体物理导论 第 7 章 能带 7.1 近自由电子模型 2π V x Vn e in x a n0势场为实数, V x V x因此势场的傅里叶分量满足 Vn V n系统
哈密顿量及薛定谔方程可写为 H H H 0 H H E 0 2 2 2π d H Vn e in x H 0 a 2 m dx 2 n0 3 固体物理导论 第 7 章 能带 7.1 近自由电子模型 H0 为自由电子的哈密顿
量,其本征函数为自由电子的本征函数 1 ikx LNa 一维晶体的 H E 0 0 0 0 x 0 k e L 长度,N 原胞数k 满足自由电子的色散关系,即能量本征值为 2k 2 E 0 k 2m周
期性边界条件 2π k0 x L k0 x k s s Z L 4 固体物理导论 第 7 章 能带 7.1 近自
由电子模型 2π H Vn e in x a n0 可看作微扰,可得一级微扰能量 L E k H kk k0 Hk0 dx 1 0 2π 2π 1 1 Vn e ikx e e dx Vn e L in x Na in x a ikx a dx n0 L 0 n0 L 0当 n?0
时,上式积分为 0,因此 E 1 k 0 所以必须计及二级微扰 5固体物理导论 第 7 章
能带 7.1 近自由电子模型二级微扰能量为 H kk 2 E 2 k 0 k E k E 0 k 其中
2π 1 L ikx in a x ikx k Hk dx Vn e e L H kk 0 0 e dx 0 L 0 n0 2π 1 L i n a k k x
Vn e dx L 0 n01当 k’-k?2n/a 时,由于 k2s/L s?Z 上式积分为02当 k’-k2n/a 倒格矢
时,上式积分的值为 L H kk Vn k k 2 nπ / a n0 6 固体物理导论 第 7 章 能带
7.1 近自由电子模型二级微扰能量对 k’ 的求和可转化为对倒格矢求和 H kk 2 Vn 2E 2 k 0 2 E k E k n 2 2 0 2π 2 k k k n 2m 2m a由此得到计及二级微
扰后的能量为 E k E 0 k E 2 k 2 2 Vn 2 k 2 2m 2 2 2π 2 n k k n 2m 2m a
7 固体物理导论 第 7 章 能带 7.1 近自由电子模型 一级微扰波函数为 H kk 1 0 k 0 E k E 0 k k k 2π ik n x a Vn e 2 2 2 2π 2 L n k k n 2m 2m a考虑了一级修正
后的波函数 2π in x eikx Vn e a k k0 k1 1 2 2 L 2 2π 2 n k k n 2m 2m a 8固体物理
导论 第 7 章 能带 7.1 近自由电子模型 注意:得到的上述微扰能量和波函数的适
用性要求 k 2与 k n 2 π/a 2 的差别较大。 如果这两者相差甚微,将导致修正能量
Vn 2 E 2 k 2 2 2 2π 2 n k k n 2m 2m a发散,结果是没有意义的。这时以 k 和 k
n2π/a标志的自由电子的状态接近简并,必须采用简并微扰论来处理 9固体物理导论
第 7 章 能带 7.1 近自由电子模型 7.1. 2 能隙由来 2π 2 π 如果 k n k 2 即 k n a a则二级微扰能量发散,因此 k 在 –n/a 附近,即 π k n 1 为小量 a时,应以 0 Ak0 Bk 作为零级波函数,并将其 0作为薛定谔方程的近似解,有 H 0 H Ak0 Bk E Ak0 Bk 0 0 2π π k k n n 1 a a 10固体物理导论 第 7 章 能带 7.1 近自由电子模
型 H 0 H E k0 A H 0 H E k B 0 0分别对上式乘以 k 和 k 并对一维空间积分,得
0 0 E E 0 k A V n B 0 Vn A E E 0 k B 0其中利用到 的正交归一性 0 k k0 k kk 0以及 k0 H 0k0 E 0 k k0 Hk0 H kk 0 k0 Ek0 E k Hk0 Vn 0 k0 Hk
V n 0 11 固体物理导论 第 7 章 能带 7.1 近自由电子模型 E E 0 k A V n B 0 Vn A E E 0 k B 0关于 A、B 的齐次方程具有非零解的条件 E E 0 k Vn 0 V n Vn Vn E E k 0 1 2因此 E E 0 k E 0 k E 0 k E 0 k 2 4 Vn 2 E Tn 1 2 Vn 2
4Tn2 2 2 π 2 其中 Tn n 2m a 12固体物理导论 第 7 章 能带 7.1 近自由电子模型 E Tn 1 2 Vn 2 4Tn2 2由于 为小量,上式第二项用泰勒展开到一阶项 2Tn 2 E k Tn Vn Tn 1 Vn 2Tn E k Tn Vn Tn 12 Vn π π 2 π 2 k n 1 k n /n 2 a a a nπ 2 nπ 2 E k an bn k E k cn d n k a a an bn cn d n 0 13固体物理导论 第 7 章 能带 7.1 近自由电子模型 nπ 2 nπ 2 E k an bn k E k cn d n k a a
上式说明,在 k-n/a 附近,电子的色散具有抛物线的形式,而且 Ek 要么大于 anTnVn,要么小于 cnTn-Vn,即存在 2Vn 范围的能量禁区,这就是能隙 对于 k 与-n/a 相距稍远的范围,已可适用非简并微扰论,电子的能量与自由电子的能量相差无几 14固体物理导论 第 7 章 能带 7.1 近自由电子模型 能带图 粗线:扩展布里渊区图式 粗线在倒空间延拓-细线 细线:周期布里渊区图式 -/a/a 之间: 约化布里渊区图式 在约化区内,电子能 量表示成若干能带, 能带之间为带隙 在每个能带中,有确定的色散关系 Enk, n 为能带的标记 15 固体物理导论 第 7 章 能带 7.1 近自由电子模型 nπ 2 nπ 2 E k an bn k E k cn d n k a a k-n/a 正是布里渊区的边界,电子能量不连续发生在布里渊区边界处 在一维的情形,这就对应于禁带的出现,禁带的宽度是周期势傅里叶分量的两倍,表明禁带的出现是电子在周期场中运动的必然结果 2π H Vn e a in x n 弱周期场:在近自由电子近似中,上式可作为微扰 的条件是傅里叶分量的绝对值远小于波矢为相应布里渊 区边界处的自由电子的动能 Tn 2 nπ 2 2m a 16固体物理导论 第 7 章 能带 7.1 近自由电子模型 禁带形成的物理 2π in x eikx Vn e a k k0 k1 1 2 2 L 2 2π 2 n k k n 2m 2m a 入射波 散射波 在波矢偏离布里渊区边界较远的情形,上式是电子波函数较好的近似。其实可将上式理解为一波矢为 k 的自由电子入射晶体的结果,第一项为入射波,第二项为散射波,散射波的幅度都很小,对入射波的干扰甚小,于是电子态与自由电子相差甚微(即近自由电子) 17固体物理导论 第 7 章 能带 7.1 近自由电子模型 当入射的自由电子波矢接近布里渊区边界 –n/a 时,与其波矢相差为倒格矢 2n/a 的散射波幅度甚大,与入射波的干涉会形成驻波,这正是 0 Ak0 Bk 0的含义,第二项正代表这一大幅度的散射波。从而具有这样的能量的电子波不能进入晶体,不能在晶体中运动,正是禁带的意义所在。事实上,由 kn/a 可得,2an,这正是一维的布拉格条件 18 固体物理导论 第 7 章 能带 7.1 近自由电子模型 7.1. 3 三维情况 在三维情况下,将周期势展开成傅里叶级数 V r VG e V0 VG e iG r iG r G G 平均势场,可令 V00 求和不包括 G 0其中 G 为任意倒格矢 G h1b1 h2b2 h3b3系统的哈密度量及薛定谔方程可写为 H H H H H r E r 0 0 2 H 0 2 H V r VG eiGr 2m G
19 固体物理导论 第 7 章 能带 7.1 近自由电子模型 H0 的本征函数是自由电子波函数 1 ikr k k k k 0 0 k 0 e V V 为晶体体积 正交归一相应的本征值为 2k 2 E 0 k 2m一级微扰能量 E k H kk k Hk dV 1 0 0 1 iGr VG e dV VG G 0 0 G V G
20
范文三:53 三维近自由电子近似及Brillouin区
5.3 三维近自由电子近似及Brillouin 区
一.三维简立方晶格中的近自由电子近似计算 1. 前提有V Na
3
晶体为立方体
边长为
L
r k
体积为V
L 3
原胞数N 晶格常数a
r r i k r ?r r
r 由Bloch 定理知电子的波函数ψ(r ) =u k (r ) e
r
由Born-Karman 边界条件[u k r (r ) 自然满足]?ψk r
(0, y , z ) =ψk r (L , y , z ) ?
?ψk r (x , 0, z ) =ψk r (x , L , z )
?ψr (x , y , 0) =ψr (x , y , L )
k ?k
e i k x L =1 等
r 2πn y 2πn x 2πn z
得k x =, k y =, k z = 量子数n x , n y , n z 为整数状态k 点
L L L r 8π38π3在k 空间均匀分布平均每个点占有体积=
V Na 3
r
2. 在k
空间作倒格子
r 2π→r r 2π→02π→00
(1).倒格子基矢b 1=i , b 2=j , b 1=k 仍为简立方格
a a a 8π3
子倒格子原胞体积?*=3
a
8π38π3
(2).每个倒格子原胞所含的状态点数3÷=N
即原胞数3
a Na (3).考虑电子自旋置
(1).零级近似 E (2).微扰修正
′r k r =0, E k (r 2) = E k (r 1) =H k
方俊鑫书用H ′
2r r
k k ′(0) r k
每个倒格子原胞所含的电子状态数2
N
r
3. 用近自由电子近似法计算在k 空间即倒格子空间电子能量跃变位
r 2
k =2m
2
r r
r i k ?r
, ψ(r ) =Ae
(0) r k
r r k ′≠k
∑E
′r ′k r H k
(0) r k
2
(注法
r r r
黄书用H ′= r r k ′k ) ?E k (r 0 ′ 模方一样) v r ≠0的条件′ H k ′k r r r r r r r r 2π→2π→2π→000 k ′=k ?(n 1i +n 2j +n 3k ) =k ?(n 1b 1+n 2b 2+n 3b 3) =k ?G n a a a r 其中n 1 n 2 n 3为整数不同时为零G n 为倒格矢 531 发生简并的条件 E =E r r r ?k ′=k ?G n 联立?r 2r 2 ?k ′=k r 2r r 2r 2r r r 2 解之 k =(k ?G n ) =k ?2k ?G n +G n r r r r r G n 121r k ?G n =G n 即 k ?=G n 22G n r (3).结论电子能量跃变的k 所满足的方程面 具有一般性 自注 二.Brillouin 区 (0) r k ′(0) r k r 2r 2 即k ′=k r 为原点到倒格点G n 连线的中垂 有个别情况不成立 但反之 1. 定义及作法 r 在k 空间即倒格子空间选取某一倒格点为原点作由原点出发的所有倒格 r r 矢的垂直平分面某一k 点和原点的连线若与n 个平面相交则此k 点所在的区域为第(n +1)布里渊区 作法 2.性质 P.176 包含原点的那一个区域为第一布里渊区刚好把第n 布里渊区的外表 面覆盖起来的所有小区域的总和为第n +1布里渊区 r (1). 对任一布里渊区中的任一k 态格矢的对应点 (2). 各布里渊区的体积都相等 (3). 每个布里渊区含N 等于倒格子原胞的体积 r 原胞数个k 态点即2N 个电子状态 在其中电子的能量准连续 其他各区都是由若干小区域 都能在其他布里渊区中找到相差一个倒 (4). 每个布里渊区对应一个能带组成 (5). 除第一布里渊区是一个连通小区域以外 r (6). 把各布里渊区通过平移倒格矢就都可以进入第一布里渊区k 只取第 r 一区的值不同能带的能量用脚标区别标记成E α(k ) 这样的第一布里渊区称为简约布里渊区 三. Brillouin 区的作法举例 1. 二维正方格子 r r r r (1).正格子基矢a 1=a i , a 2=a j r 2πr r (2).倒格子基矢 b 1=i =b i , a (3).作倒格子点 ±b , 0 在倒格子空间0, ±b 连线的中垂线 r r b 2=b j 倒格子还是正方格子 第一类 倒格 作原点倒格点和四个最近邻 第一类线 由它们围成的正方形因不 532 受后面各类线的影响线渊区 即是第一布里渊区 ( 书P.177图 4-10 第二类倒格点 ±b , ±b 连线的中垂线 第二类 即是第二布里 再作原点和四个次近邻 它们和第一类线围成的四个小块因不受后面各类线的影响方书上P.234画出了前四个布里渊区 王书P.193 图 注意并不是每多画一类线就增加一个布里渊区关键是看外面的线对里面 [展示自画图] r r r r r r a 1=a i , a 2=a j , a 3=a k r 2πr r r r r r b 1=i =b i , b 2=b j , b 3=b k a 作原点和六个最近邻倒格点±b , 0, 0 ±b , ±b , 0王书 P.195 图 ±b , 0, ± b 自画图 0, ±b , 0, 的区有无影响 2. 简立方格子 (1)正格子基矢 (2) 倒格子基矢 倒格子还是简立方格子 (3)0 在倒格子空间0, 0, ±b 连线的中垂面 这六个平面围成的立方体就是第一布里渊区 再作原点和十二个次近邻倒格点±b , ±b 连线的中垂面 区的六个小区域 就是第二布里渊区 这十二个面和原来的六个面所围成的包围第一布里渊 3. 体心立方格子 r a r r r r a r r r r a r r r 正格子基矢a 1= (?i +j +k ) , a 2=(i ?j +k ) , a 3=(i +j ?k ) 222r 2πr r r r r r r r r r (j +k ) =b (j +k ) , b 2=b (i +k ) , b 3=b (i +j ) 倒格子基矢b 1=a 倒格子是面心立方格子作原点和十二个最近邻倒格点±b , ±b , 00, ± b 布里渊区 0, ±b , ±b 连线的中垂面 这十二个面围成的十二面体 王书 P.195图 ( 书P.179图4-12 )[模型] ±b , 就是第一 4. 面心立方格子 r a r r r a r r r a r r 正格子基矢a 1= (j +k ) , a 2=(i +k ) , a 3=(i +j ) 222 倒格子基矢 r 2πr r r r r r r r r r r r r b 1=(?i +j +k ) =b (j +k ) , b 2=b (i ?j +k ) , b 3=b (i +j ?k ) a 倒格子是体心立方格子作原点和八个最近邻倒格点±b , ±b , ±b 的中垂面中垂面八面体 这六个平面截去前面八面体的六个顶角使之成为十四面体就是第一布里渊区 ( 书P.179 图4-13 )王书 P.198图 连线 这八个面围成一个封闭八面体再作原点和六个次近邻倒格点连线的 亦称截角 533 作业 P.5824.8 [ 第(3)问可不做 ] ; 一平面正交晶格 矩形原胞的边长为a 1=2A 和a 2=4A o o 补充题画出它 的第一和第二布里渊区 534 一维周期场电子运动的近自由电子近似 摘要: 布洛赫定理,是从周期场所具有的平移对称性出发,得出了在周期势场中运动的电子波函数的普遍形式,但不能给出某一晶体电子波函数的具体形式,也不能获得电子能谱——能带结构的表达形式。要获得这些知识,必须求解公式。这是一个比较困难的问题,为此,我们先讨论能带理论中的一个简单模型——近自由电子近似。这个模型适用于周期场较弱的情况,故也叫弱周期场近似。由于周期场的周期性起伏很弱,它可以看成自由电子情况稳定势场的微扰,此时晶体中的价电子行为就很接近自由电子,故也叫自由电子近似。这个模型虽然简单,但是却能给出周期场中运动电子本征态的一些最基本特点。 关键词:能带理论;周期场;微扰;近自由电子近似 一维周期场中电子运动的近自由电子近似 这是一个一维的模型,通过这个模型的讨论,可以进一步了解在周期场中运动的电子本征态一些最基本的特点。 图1中画出了一维周期场的示意图。所谓近自由电子近似是假定周期场的起伏比较小,作为零级近似,可以用势场的平均值代替V(x)。把周期起伏 [V(X)- 〕做为微扰来处理。 图1一维周期场 零级近似的波动方程为 它的解便是恒定场中自由粒子的解 (1) (2) 上式在归一化因子中引入晶格长度L=Na,为原胞的数目,a是晶格常数(原子间距)。引入周期性边界条件可以得到k只能取下列值 很容易验证波函数满足正交归一化条件。 (3) (4) 由于零级近似下的解为自由电子,所以称为近自由电子近似。按照一般微扰理论的结果,本征值的一级和二级修正为 (5) 波函数的一级修正为 (6) 其中微扰项 具体写出 为 (7) 其中前一项,按定义就等于平均势场,因此能量的一级修正为0。 和 都需要计算矩阵元 ,由于k和k两态之间的正交关系 , 现在我们证明,由于V(x)的周期性,上述矩阵元服从严格的选择定则。将 按原胞划分写成 对不同的原胞n,引入积分变数 并考虑到V(x)的周期性 就可以把前式(7)写成 (8) 现在区分两种情况: (1) ,即k和k相差 式内各项均为1, 因此 , ,在这种情况下,显然,(8)式中的加 (2) 成 (9) ,在这种情况下,(13)式中的加式可用几何级数的结果写 K和k又可写成{见(4)式 } 因此,上式中的分子 同时,分母由于 ,所以不为零,在这种情况下,矩阵元(8)恒为零。 综合以上,我们得到,如果 ,则 , 否则 (10) 很容易看到,上式中以Vn表示的积分实际上正是周期场V(x)的第n个傅立叶系数。 根据这个结果,波函数考虑了一级修正(8)式后可以写成 : (11) 连加式的指数函数,在x改变a的整数倍时,是不变的,这说明括号内为一周期函数。这类似于布洛赫函数的形式:可以写成一个自由粒子波函数乘上具有晶格周期性的函数。 根据(10),二级微扰能量可以写成 值得特别注意的是,当 也就是 时,趋向 趋于 (12) (13) (14) 整数倍时,E (2) k , n表任意一个整数,也就是说,当k 为 。很显然,该结果是没有意义的。它只说明,以上的微扰论方法,对于 在(14)式附近的k是发散的,因此不适用。 总结: 在零级近似中,电子作为自由电子,其能量本征值 Ek k=± nπa Ek 与k的关系曲线是抛 2n 物线,在周期势场的微扰下,曲线在处断开,能量突变值为。 在诸能带断开的间隔内不存在允许的电子能级,称为禁带,禁带的位置及宽度取决于晶体的结构和势场的函数形式。 另一方面,对于波矢 k= lN?2πa 而言,N很大,故k很密集,可以认为 En(k) 是k的准连续函数,这些准连续的能级被禁带隔开而形成一系列能带1,2,3…。不难算出,每个能带所对应的k的取值范围都是2π/a,即一个倒格子原胞长度,而所包含的量子态数目是N,等于晶体中原胞的数目。 En(k) 总体称为能带结构(n为能带编号),相邻两个能带 En(k) 与 En+1(k) 之 间可以相接,重叠或是分开,对于一维周期性势场来说属于分开情况,则出现带隙——禁带。 参考文献: [1].固体物理学[M],上海科学技术出版社,方俊鑫,路栋,1981. [2].固体能带理论[M],复旦大学出版社,谢希德,1998. [3].固体物理学[M],上海科学技术,蒋平,2003. [4].材料科学导论[M],化学工业出版社,冯瑞,2002. 导读:就爱阅读网友为您分享以下“一维周期场电子运动的近自由电子近似”资讯,希望对您有所帮助,感谢您对92to.com的支持! 一维周期场电子运动的近自由电子近似 摘要: 布洛赫定理,是从周期场所具有的平移对称性出发,得出了在周期势场中运动的电子波函数的普遍形式,但不能给出某一晶体电子波函数的具体形式,也不能获得电子能谱——能带结构的表达形式。要获得这些知识,必须求解公式。这是一个比较困难的问题,为此,我们先讨论能带理论中的一个简单模型——近自由电子近似。这个模型适用于周期场较弱的情况,故也叫弱周期场近似。由于周期场的周期性起伏很弱,它可以看成自由电子情况稳定势场的微扰,此时晶体 1 中的价电子行为就很接近自由电子,故也叫自由电子近似。这个模型虽然简单,但是却能给出周期场中运动电子本征态的一些最基本特点。 关键词:能带理论;周期场;微扰;近自由电子近似 一维周期场中电子运动的近自由电子近似 这是一个一维的模型,通过这个模型的讨论,可以进一步了解在周期场中运动的电子本征态一些最基本的特点。 图1中画出了一维周期场的示意图。所谓近自由电子近似是假定周期场的起伏比较小,作为零级近似,可以用势场的平均值代替V(x)。把周期起伏 [V(X)- 〕做为微扰来处理。 图1一维周期场 零级近似的波动方程为 它的解便是恒定场中自由粒子的解 (1) (2) 上式在归一化因子中引入晶格长度L=Na,为原胞的数目,a是晶格常数(原子间距)。引入周期性边界条件可以得到k只能取下列值 2 很容易验证波函数满足正交归一化条件。 (3) (4) 由于零级近似下的解为自由电子,所以称为近自由电子近似。按照一般微扰理论的结果,本征值的一级和二级修正为 (5) 波函数的一级修正为 (6) 其中微扰项 具体写出为 (7) 其中前一项,按定义就等于平均势场,因此能量的一级修正为0。 和都需要计算矩阵元,由于k和k两态之间的正交关系 , 现在我们证明,由于V(x)的周期性,上述矩阵元服从严格 3 的选择定则。将 按原胞划分写成 对不同的原胞n,引入积分变数 并考虑到V(x)的周期性 就可以把前式(7)写成 (8) 现在区分两种情况: (1) ,即k和k相差 式内各项均为1, 因此 ,,在这种情况下,显然,(8)式中的加 (2) 成 (9) ,在这种情况下,(13)式中的加式可用几何级数的 4 结果写 K和k又可写成{见(4)式 } 因此,上式中的分子 同时,分母由于 ,所以不为零,在这种情况下,矩阵元(8)恒为零。 综合以上,我们得到,如果 ,则 , 否则 (10) 很容易看到,上式中以Vn表示的积分实际上正是周期场V(x)的第n个傅立叶系数。 根据这个结果,波函数考虑了一级修正(8)式后可以写成 : (11) 5 连加式的指数函数,在x改变a的整数倍时,是不变的,这说明括号内为一周期函数。这类似于布洛赫函数的形式:可以写成一个自由粒子波函数乘上具有晶格周期性的函数。 根据(10),二级微扰能量可以写成 值得特别注意的是,当 也就是 时,趋向 趋于 (12) (13) (14) 整数倍时,E (2) k , n表任意一个整数,也就是说,当k 为 。很显然,该结果是没有意义的。它只说明,以上的微扰论方法,对于 在(14)式附近的k是发散的,因此不适用。 总结: 在零级近似中,电子作为自由电子,其能量本征值 6 Ek k n a Ek 与k的关系曲线是抛 2n 物线,在周期势场的微扰下,曲线在处断开,能量突变值为。 在诸能带断开的间隔内不存在允许的电子能级,称为禁带,禁带的位置及宽度取决于晶体的结构和势场的函数形式。 另一方面,对于波矢 k lN 2 a 而言,N很大,故k很密集,可以认为 En(k) 是k的准连续函数,这些准连续的能级被禁带隔开而形成一系列能带1,2,3…。不难算出,每个能带所对应的k的取值范围都是2π/a,即一个倒格子原胞长度,而所包含的量子态数目是N,等于晶体中原胞的数目。 En(k) 总体称为能带结构(n为能带编号),相邻两个能带 7 En(k) 与 En,1(k) 之 间可以相接,重叠或是分开,对于一维周期性势场来说属于分开情况,则出现带隙——禁带。 参考文献: [1].固体物理学[M],上海科学技术出版社,方俊鑫,路栋,1981. [2].固体能带理论[M],复旦大学出版社,谢希德,1998. [3].固体物理学[M],上海科学技术,蒋平,2003. [4].材料科学导论[M],化学工业出版社,冯瑞,2002. 百度搜索“就爱阅读”,专业资料,生活学习,尽在就爱阅读网92to.com,您的在线图书馆 8范文四:一维周期场电子运动的近自由电子近似
范文五:周期信号 基波近似 一维周期场电子运动的近自由电子近似



 谁能给我想要的幸福
谁能给我想要的幸福

