正方形的面积,边长×边长 正方形的周长,边长×4 正方形 S=a×a 边长 (a) C=4a 2 S=a
长方形的周长,(长+宽)×2 宽(b) 长方形的面积,长×宽 长方形 C=(a+b)×2 S=a×b C=2(a+b) 长(a)
平行四边形的面积,底×高 高(h) 平行四边形 S=a×h 周长等于一周四条边的长度 S=ah 底(a)
三角形的面积,底×高?2 高(h) 三角形 S=a×h?2 周长等于一周三条边的长度 S=ah?2 底(a)
上底(a)
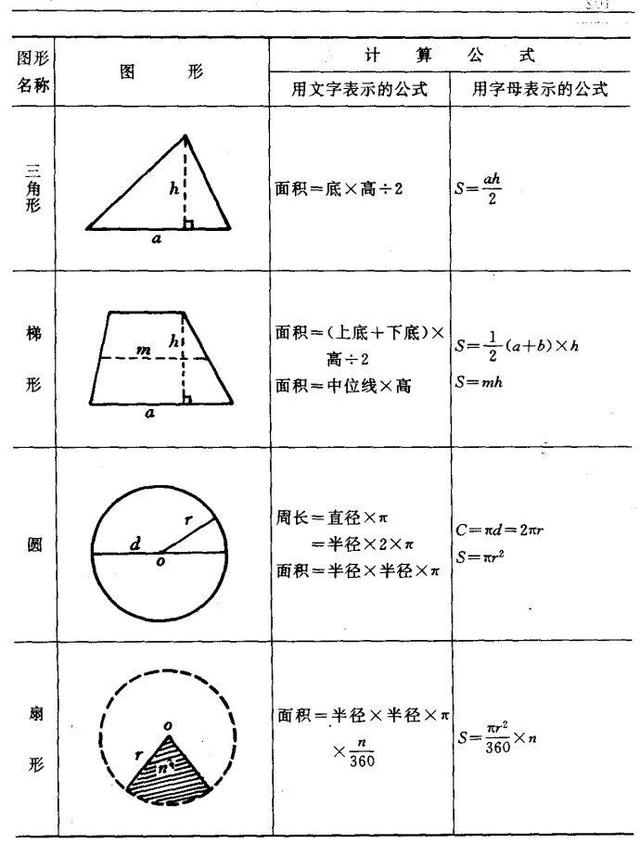
梯形的面积,(上底+下底)×高?2
梯形 高(h) S=(a+b)×h?2 周长等于一周四条边的长度
S=(a+b)h?2 下底(b)
多边形公式
内角
正n 边形的内角和度数为:(n -2)×180度;
正n 边形的一个内角是(n-2)×180°÷n.
外角
正n 边形外角和等于n·180°-(n-2)·180°=360°
所以正n 边形的一个外角为:360÷n.
所以正n 边形的一个内角也可以用这个公式:180°-360÷n.
中心角
任何一个正多边形,都可作一个外接圆,多边形的中心就是所作外接圆的圆心,所以每条边的中心角,实际上就是这条边所对的弧的圆心角,因此这个角就是360度÷边数。
正多边形中心角:360÷n
对角线
在一个正多边形中,所有的顶点可以与除了他相邻的两个顶点的其他顶点连线,就成了顶点数减2(2是那两个相邻的点)个三角形。而正多边形的顶点数与边数相同,所以用边数减2个三角形。三角形内角和:180度,所以把边数减2乘上180度,就是这个正多边形的内角和对角线
对角线数量的计算公式:n(n-3)÷2。
面积
设正n 边形的半径为R ,边长为an ,中心角为αn ,边心距为r n ,则αn=360°÷n,an =2Rsin(180°÷n),r n=Rcos(180°÷n),R^2=r n^2+(an÷2)^2,周长pn=n×an,面积Sn=pn×rn÷2。
对称轴
正多边形的对称轴——
奇数边:连接一个顶点和顶点所对的边的中点,即为对称轴;
偶数边:连接相对的两个边的中点,或者连接相对称的两个顶点,都是对称轴。 正N 边形边数为N 。
正N 边形角数为N 。
正N 边形对称轴数都为N 条(如三角形有奇数条边,N=3,有三条对称轴;正方形有偶数条边,N=4,有四条对称轴)
多边形染色公式
【公式】用红、黄、蓝三色给边长互补相等的五边形染色问题 用红、黄、蓝三色给边长为3,4,5,6,7的五边形的各边染色,要求相邻两边不许同色,共有多少种不同的染法
--------------
公式:Sn =2^n+2*(-1)^n
n=5
则 S5=2^5+2*(-1)^5=30
-------------------------------------------------------------
设把n 边形分成边B1,B2,…,Bn. 开始时,可以给B1涂以任何一种颜色. 所以B1有3种染法. B1染后,B2的染法有2种(涂上B1以外的2种颜色). B3染色方法也有2种,这是因为B3可以与B1同色. ,后面的都是可以这样看,一直到Bn 都是2种(先不考虑Bn 和B1相同),染色方法的总数为3×2^(n-1)种.
现在我们来考虑 当Bn 和B1同色的情况有多少种. 设有某一种染法使Bn 与B1同色,n-1个多边形时同色不相邻的染法. 因此,多边形数为n 时,染法的总数为S(n). 于是得到函数方程
S(n)+S(n-1)=3*2^(n-1)
推导这个函数 对S(n)*(-1)^n 可得到
(-1)^n*S(n)-(-1)^(n-1)*S(n-1)=-3*2^(n-1) 采用递归做法 结合上面的
公式
可以得到 S(n)=2^n+2*(-1)^n
给个例题:
一个不规则的10边形, 现在有红,黄,兰 三色来给10条边涂色(三种颜色都要用上), 要求相邻两边不同色。 有多少种方法?
公式推理太麻烦,考试直接PASS ,做下题
思维活一点,5边形,相邻边异色,共3中颜色,每种颜色最多职能用到2次,否则临边有同色,配色方案只有1,2,2一种方法(不知道题意是否要求每种颜色必须用到)(同理,加入6边形,则可以存在最多用到3次的颜色,否则也会出现临边同色)
理解这一点的话就好做了! 根据1,2,2的配色方案:
(1) 红色用到1次,黄蓝各用2次 先定红色,任选1边(5条边有5种选法), 已经选好的红色有两个临边分别为黄,蓝(或者蓝,黄--又是2种选法,不存在红色的两个临边都为黄或者蓝,否则剩下的两边相邻且颜色相同)
所以得到红色用到1次的涂法有 5*2共10种 同理蓝色用到1次10种,黄色用到1次10种 共30种
逻辑清楚的话,一看就懂。 太机械的话,只有慢慢推公式了 希望有人可以分享
多边形面积公式
多边形面积公式
平行四边形面积 = 底 × 高
字母表示 s = a × h
平行四边形的底 = 平行四边形面积 ÷ 高
a= s ÷h
平行四边形的高 = 平行四边形面积 ÷ 底
h= s ÷a
三角形面积 = 底×高÷2
s = a × h ÷2
三角形的底 = 面积×2÷高
a = s × 2÷h
三角形的高 = 面积×2÷底
h = s × 2÷a
梯形的面积 =(上底+下底)×高÷2
S = (a+b ) ×h ÷2
梯形的上底 = 梯形的面积×2÷高-下底
a = s×2÷h -b
梯形的下底 = 梯形的面积×2÷高-上底
b = s×2÷h -a
梯形的高=梯形的面积×2÷(上底+下底)的和
h= s×2÷(a+b)
多边形周长的计算
多边形周长的计算
例1
计算下列图形的周长(单位:厘米) 。
思路分享:(1)将图中右上缺角处的线段分别向上、向右平行移动到虚线处(见左下图) ,这样正好移补成一个正方形,所以它的周长为25×4=100(厘米) 。
(2)与(1)类似,可以移补成一个长方形,周长为 (10+15) ×2=50(厘米) 。
【我的解疑】
1. 下图是一块小麦地, 已知条件如图中所示. 这块地的周长是米。
3. 求下图上“凹”形的周长. 单位:厘米
50
2. 下图“十”字的横与竖都长6厘米. 问“十”间的周长是厘米。
4. 下图是一块地, 四周都用篱笆围起来, 转弯处都是直角. 已知西边篱笆长17米, 南边篱笆长23米. 四周篱笆长米。
23
17
例1 在一张纸上画出由四个边长为3厘米的正方形拼凑或组合成的图形(重叠的线段只算画一次) 。显然,这个图形有多种多样的画法,下列各图是其中的一部分画法。在所有的这些画法中,
(1)哪种画法画出的线段总长最长?有多长? (2)哪种画法画出的线段总长最短?有多长?
思路分享:画的线段重叠部分越少,画的线段就越长。反之,重叠部
分越多,画的线段就越短。因此,类似图1那样画的线条最长,共画了3×4×4=48(厘米) 。右图画的线条最短,共画了(3+3) ×6=36(厘米) 。
【我的解疑】
1. 下图是一个公园的平面图,A 是公园的大门. 问:小明从A 门进公园, 不重复地沿道路走公园一圈, 他走了多少米?
2. 下图是某建设物的设计图, 如图所示(单位:米) 现根据需要在它周围绕电线一圈, 试求需电线多少米?
1
4 1 1 3
2 1 4
1 3
240
A
3. 用15个边长2厘米的小正方形摆成如下图的形状, 求图形周长是多少厘米?
转载请注明出处范文大全网 » 五年级多边形面积周长计算公式



 内涵女神苏晴儿爷
内涵女神苏晴儿爷

