范文一:数轴上任意两点间的距离公式
数轴上任意两点间的距离公式
(2002南京中考数学试题)阅读下列材料:点A、B在数轴上分别表示数a和b,A、B两点之间的距离为AB。
当A、B两点有一点在原点时,不妨设A点在原点,如图1, AB,OB,b,a,b;当A、B两点都不在原点,如图2,点A、B都在原点的右边,
AB,OB,OA,b,a,b,a,a,b;
如图3,点A、B都在原点的左边, AB,OB,OA,b,a,,b,(,a),a,b;
, A点和B点在原点的两边, AB,OB,OA,a,b,a,(,b),a,b。 如图4
综上所述,数轴上A、B两点之间的距离AB,a,b。
回答下列问题:
(1) 数轴上表示2和5的两点之间的距离是 ,数轴上表示-2和-5的两点之
间的距离是 ,数轴上表示1和-3的两点之间的距离是 ;
AB,2(2) 数轴上表示x与-1的两点A和B之间的距离是 ,如果,那么
x为 ;
x,1,x,2(3) 当代数式取最小值时,相应的x的取值范围是 。
A B
图1 O
A B
图2 O
A B
图3 O
A B
图4 O
范文二:【doc】数轴上任意两点间的距离公式
中小学教育资源站(http://www.edudown.net),百万免费教育资源当下来,无须注册~
数轴上任意两点间的距离公式
(2002南京中考数学试题)阅读下列材料:点A、B在数轴上分别表示数a和b,A、
ABB两点之间的距离为。
AB,OB,b,a,b当A、B两点有一点在原点时,不妨设A点在原点,如图1, ;当A、B两点都不在原点,如图2,点A、B都在原点的右边,AB,OB,OA,b,a,b,a,a,b;
AB,OB,OA,b,a,,b,(,a),a,b如图3,点A、B都在原点的左边, ;
AB,OB,OA,a,b,a,(,b),a,b如图4, A点和B点在原点的两边, 。
AB,a,b综上所述,数轴上A、B两点之间的距离。
回答下列问题:
(1) 数轴上表示2和5的两点之间的距离是 ,数轴上表示-2和-5的两点之
间的距离是 ,数轴上表示1和-3的两点之间的距离是 ;
AB,2-1的两点A和B之间的距离是 ,如果,那么(2) 数轴上表示x与
x为 ;
x,1,x,2(3) 当代数式取最小值时,相应的x的取值范围是 。
A B
图1 O
A B
图2 O
A B
图3 O
A B
图4 O
中小学教育资源站http://www.edudown.net
中小学教育资源站(http://www.edudown.net),百万免费教育资源当下来,无须注册~
中小学教育资源站http://www.edudown.net
范文三:[总论]数轴上随便率性两点间的距离公式
数轴上任意两点间的距离公式
(2002南京中考数学试题)阅读下列材料:点A、B在数轴上分别表示数a和b,A、B两点之间的距离为。 AB
当A、B两点有一点在原点时,不妨设A点在原点,如图1, ;当A、AB,OB,b,a,bB两点都不在原点,如图2,点A、B都在原点的右边,;AB,OB,OA,b,a,b,a,a,b
如图3,点A、B都在原点的左边, ;如图4, AB,OB,OA,b,a,,b,(,a),a,bA点和B点在原点的两边, 。AB,OB,OA,a,b,a,(,b),a,b
综上所述,数轴上A、B两点之间的距离AB,a,b。 回答下列问题:
(1) 数轴上表示2和5的两点之间的距离是 ,数轴上表示-2和-5的两点之间的距离
,数轴上表示1和-3的两点之间的距离是 ;是
AB,2(2) 数轴上表示x与-1的两点A和B之间的距离是 ,如果,那么x
为 ;
x,1,x,2(3) 当代数式取最小值时,相应的x的取值范围是 。
A B
图1 O
A B
图2 O
A B
图3 O
A B
图4 O
范文四:数轴上任意两点间的距离公式[1]
数轴上任意两点间的距离公式
(2002南京中考数学试题)阅读下列材料:点A 、B 在数轴上分别表示数a 和b ,A 、B 两点之间的距离为AB 。
当A 、B 两点有一点在原点时,不妨设A 点在原点,如图1, AB =OB =b =a -b ;当A 、B 两点都不在原点,如图2,点A 、B AB =OB -=b -a =b -a =a -b ; 如图3,点A 、B 都在原点的左边, =-=b -a =-b -(-a ) =a -b ;如图4, A 点和B 点在原点的两边, =OB +=a +b =a +(-b ) =a -b 。
综上所述,数轴上A 、B 两点之间的距离AB =a -b 。
回答下列问题:
(1) 数轴上表示2和5的两点之间的距离是 ,数轴上表示-2和-5的两点之间的距离
是 ,数轴上表示1和-3的两点之间的距离是 ;
(2) 数轴上表示x 与-1的两点A 和B 之间的距离是 ,如果AB =2,那么x
为 ;
(3) 当代数式x ++x -2取最小值时,相应的x 的取值范围是 。
范文五:初中数轴两点距离公式 两点间距离公式的应用
导读:就爱阅读网友为您分享以下“两点间距离公式的应用”的资讯,希望对您有所帮助,感谢您对92to.com的支持!
两点间距离公式的应用
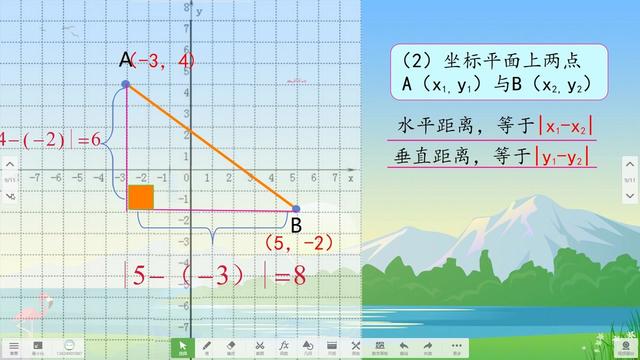
A(x1,y1)、B(x2,y2)两点间的距离公式表示为d(P1,P2),
一、求函数的值域
有些带根式的函数,在求其值域时,联想到两点间的距离公式,利用函数的几何意义可
例1解:?y
1
? 函数y(-1,1)、B(1,1)的距离之和, 由三角形的三边关系可知 | PA | , | PB | ? | AB |,当P点在线段AB上时,取得等号。
而易求得| AB | ,,?y 。
?
二、证明不等式
有些不等式的证明难以下手,但是若与两点间的距离公式联系起来,进行恰当的变形后就可以找到证明的思路。 例2、已知x1,0,x2,0
x
则 | OA | | OB | | AB |
| OA | ,| AB |,即
对于三点共线问题,有若干种证法,当然也可以用两点间的距离公式来进行证明。三点确定三条线段,若其中两条线段
2
的长度之和等于第三条线段的长,则此三点必共线。
例3、求证:A(1,5)、B(0,2)、C(2,8)三点共线。
| AB | | BC |
| AC | ? 有,从而A、B、C三点共线。
四、证明平面几何问题
有些平面几何问题借助于两点间的距离公式会很容易的得证。
例4、已知AO是?ABC中BC边上的中线。
2222证明:| AB | , | AC | ,2(| AO | , | OC |)。
分析:取BC边所在的直线为x轴,边BC的中点为原点,
建立如图所示的直角坐标系。
设
3
B(-a,0),O(0,0),C(a,0),A(m,n),其中a,0. 则由两点间的距离公式得
222222| AB | , | AC | ,( m + a ) + n
+ ( m - a ) + n ,) 22222| AO | , | OC | ,m + n + a,
2222? 证得| AB | , | AC | ,2(| AO | , | OC |)。
五、求曲线的轨迹方程
在求曲线方程的时候,好多的题目都涉及到两点间的距离公式,及公式的变形、化简。 1例6、已知动点P到定点A(0,-1)的距离与到定直线y = -9的距离的比为,求动3点P的轨迹方程。 122?,化简整理得9x + 8y – 72 = 0. 解:设P(x,y)223?动点P的轨迹方程是9x + 8y – 72 = 0.
以上是笔者在教学过程中对于两点间的距离公式的一点心得体会,只要在平时的学习过程中做一个有心人,处处、时时留心,经常地反思、总结自己做过的每一个题目,努力地从中悟出点东西来,那么,每一个同学的成绩会取得很大的
4
进步的~
百度搜索“就爱阅读”,专业资料,生活学习,尽在就爱阅读网92to.com,您的在线图书馆
5
转载请注明出处范文大全网 » 数轴上任意两点间的距离公式



 用户65181654
用户65181654

