范文一:平均场理论
第三章 多体理论:(I)平均场理论
平均场理论是量子多体理论的零级近似,是进一步近似的出发点, 也是最重要, 最流行的量子多体理论, 因而成为量子多体理论的基础。平均场理论所包含的物理概念-平均场概念,是量子多体理论的精华, 这一概念具有客观意义,是微观多体世界的最重要的属性的深刻反映。
§3-1 量子力学多体问题[1]
A.量子多体系统与量子多体问题
量子力学问题,绝大多数是量子多体系统的问题,这包括:1. 量子多体系统结构的研究,如原子、分子、原子核的结构,固体的结构及其电磁性质。2.量子多体系统碰撞与反应过程的研究,如原子、分子碰撞、原子核碰撞与反应截面的计算。3. 量子多体系统衰变性质的研究,如原子、分子的发光,原子核的α、β、γ衰变与裂变。
量子多体系统的分类:
按照粒子的种类,量子多体系统分为:① 费米子系统,② 玻色子系统,③ 费米子—玻色子混杂系统。上述系统各自对应的例子:①如原子,分子中的电子系统,原子核系统,固体中的电子系统; ②如固体中的声子系统,光子系统; ③如固体中电子——声子系统,激光与原子相互作用系统。
按照微观粒子相互作用的强弱,多体系统可分为:1弱作用或弱耦合系统,如电磁作用与弱作用系统;2.强作用或强耦合系统,如原子核系统,电子强耦合系统。
非相对论量子多体理论的任务是从多体相互作用和多体薛定格方程出发,计算多体系统的各种性质。
B.量子多体理论:微观理论和等效理论
量子多体理论可分为: 从第一原理出发的微观多体理论和从等效相互作用出发的唯象或半唯象理论(等效理论和模型理论)。
由于量子多体问题的复杂性,除少数量子多体问题(如氢原子问题)外,绝大多数量子多体系统很难从第一原理出发求解,合理的近似成为求解量子多体问题的关键,其中平均场理论是最成功的近似理论,成为处理量子多体问题的其他各种理论方法的出发点,也是建立各种等效相互作用理论的基础。
C.微扰理论和非微扰理论
平均场理论本身就是非微扰的。在平均场近似的基础,可以得到零级近似的
?,系统的H?可以写成 哈密顿量H0
?=H?+V (3-1) H0res
平均场近似是最简单的非微扰理论,它通过自洽场方法把相互作用的主要部分包括到平均场之中,使得剩余相互作用Vres变得比较微弱,因而可以用微扰论方法求解。 基于平均场的微扰论在原子物理和原子核物理的某些问题的处理中相当成功。
但是, 对于另一些问题,特别是核物理中的问题和固体物理中的强关联问题,
对剩余相互作用Vres作微扰处理仍不能得到好的结果,这就需要发展处理Vres的非微扰理论,这是第4、5两章要研究的问题。
§3-2 平均场理论:最简单的非微扰理论和处理多体问题的出发点
[2-3]
A.平均场理论的基本思想
存在相互作用的多粒子系统,每个粒子都受到周围其他粒子的作用,这些周围粒子的相互作用的迭加并对其粒子密度分布(粒子云)的平均,在零级近似下,将产生一个平均势场。这个平均势场是一个单体算符,只依赖于受作用的这个粒子的坐标,但不是外界施加的外场,而是其他粒子对这个粒子相互作用迭加平均的结果。这个平均场一般随时间变化,但在定态极限下,它是静态的。对于全同粒子系统,特别是费米子系统,由于多体系统波函数或密度矩阵中存在着交换项,平均场相应地也包含一个非定域的交换项,它与动量相关势场等效。对于带自旋的粒子,平均场还包含自旋一轨道力。
?包含一体算符(只依赖一个粒子对于二体相互作用的多体系统,哈密顿量H
的坐标)的动能项和二体算符(只依赖两个粒子的坐标)的相互作用项。而平均场是单体算符,它虽然可以包含二体相互作用的主要效应,但不能完全代替二体相互作用项,只能是对二体相互作用的单体近似。这些不能用平均场概括的二体相互作用,称为剩余相互作用Vres 。 因此,考虑了平均场以后,系统有一个由平均场
?(又称独立粒子近似下的哈密顿量)单体算子组成的哈密顿量H,还有一个平均0
场不能包括的二体剩余相互作用Vres。系统总的哈密顿量应为二者之和,?=H?+V。H?产生平均场支配下的系统的独立粒子运动,类似于外场作用H0res0
? 破坏独立粒子运动, 把这些独立粒下产生的独立粒子运动;而剩余相互作用Vres
子运动耦合起来,产生各种各样的多体关联,以至于集体运动。
多体系统中粒子-粒子相互作用产生平均场的过程, 对于定态问题, 是一个非线性的自洽反馈的过程:具有确定量子态的各个粒子对某个粒子相互作用的迭加并对这些粒子的密度分布求平均后,产生了一个单体平场场;这个单体的平均场反过来又产生出各个粒子的确定的量子运动;即所有粒子的量子状态决定了平均场,而平均场又产生出各个粒子的量子运动,这样就形成一个非线性的反馈过程。对于定态, 这个过程必须达到自洽:产生平均场U的各粒子的量子态ψα应当是平均场产生的量子态,产生各量子态的平均场应当是各量子态生成的平均场,即ψα→U→ψα或U→ψα→U。
总之,平均场理论的基本思想是:1)多体系统各粒子对某一粒子相互作用的迭加和平均,产生一个平均场;2)这个平均是单体算符,包括非定域(动量有关)项和自旋-轨道力;3)产生平均场的过程是一个非线性反馈的过程;对定态问题, 还要求自洽; 4)平均场是对多体系统相互作用的非微扰的零级近似,对多体系统的正确描述应当是平均场加剩余相互作用;5)平均场产生多体系统的独立粒子运动,而剩余相互作用要破坏这种独立粒子运动,引起量子态跃迁,产生粒子之间的多体关联,导致集团运动和集体运动。
B.平均场近似:时间有关的Hartree-Fock理论(TDHF)与Hartree-Fock理论(HF)
如上所述,在平均场近似下,剩余相互作用被略去,系统的哈密顿量成为单体算符,各个粒子在平均场中彼此独立地运动, 粒子之间通过平均场相互联系, 互通信息。因此,平均场近似又称独立粒子近似。与外场中的独立粒子运动不同,平均场近似下的独立粒子运动的量子态和产生这些量子态的平均场必须有互为因果的反馈关系。因此,自洽平均场是随多粒子系统各粒子的量子态的变化而变化的,不像外场是固定不变的。
1.时间有关的平均场近似:TDHF
在时间有关的平均场近似下,每个粒子都有随时间变化的独立的量子态, 因r此可以假定系统中A个粒子占据A个时间有关的单粒子态?α(r,t),满足正交归一化条件
α|?β=δαβ (3-2)
对于费米子系统,多体系统的波函数应当是反对称化的;在独立粒子近似下,它应当是A个粒子的波函数的乘积的完全反对称化组合,即应是一个Slater行列式,
1ΦA(1?A)=(?1)pP?α1(1)?α2(2)L?αA(A) ∑A!p
?α1(1)?α1(2)L?α1(A)
?α2(1)?α2(2)L?α2(A)1 (3-3) det=LA!
αA(1)?αA(2)L?αA(A)[]
例子:2粒子系统
2
在独立粒子近似(即平均场近似)下,时间有关的薛定格方程
?ψA?ψ (3-4) =H ihA?t
应当限制在独立粒子近似波函数ΦA这个子空间内求解:
ψA?ΦA (3-5)
?ΦA?Φ (3-6) ih?HA?t
在二体相互作用情况
2AA?p1i?=∑H+∑V(ij) (3-7) 2m2i≠ji=1
时间有关薛定格方程的推导:
(1)严格解:时间有关的薛定格方程(3-4)可用作用量变分极小原理得到。 定义作用量
??|ψ=ψ*(ih??H?)ψdxdt I[ψA]=∫dtψA|ih?HAA∫A?t?t
考虑ψ*A在整个Hilbert空间的变分, 由作用量变分极小得
δψ?I[ψA]=0 (3-8) AΦ2(1,2)=1[?1(1)?2(2)??1(2)?2(1)]
??)ψdxdt=0 ?HA?t
由于δψ*A任意,被积函数必为零, 因此得时间有关的薛定格方程,
??)ψ=0 (3-9) (ih?HA?t
(2) 独立粒子近似解:若把变分限制在独立粒子近似确定的子空间(Slater行列式ΦA)内进行, 则得到TDHF方程。 步骤如下:
限制变分子空间到ΦA:
ψA?ΦA(1LA) (3-10)
在这个子空间计算作用量:
??|Φ (3-11) I[ΦA]=∫dtΦA|ih?HA?t
?12p???=∫dt{∑∫?α'(1t)ih?α'(1t)d1?∑∫?α′(1t)?α′(1t)d1
'?t2mα′α
1???∑∫?α?α'(1t)?β′(2t)??α'(2t)?β′(1t)]d1d2} ′(1t)?β′(2t)V(12)[2α′β′
其中di=dxi, (it)=(xi,t)。在这个子空间对作用量变分: ?δψ∫A(ih
δ?*αI[ΦA]=0 (3-12)
??α(1t)p12?∫δ?α(1t)ih?td1dt?∫δ?α(1t)2mα(1t)d1dt?
?∑∫δ?α(1t)?β′(2t)U(12)(?β'(2t)?α(1t)??β'(1t)?α(2t))d2d1dt=0*?
β′
由于δ?*α任意,得到TDHF方程:
?2??αpih??α?∑∫d2?β?(2t)U(12)[?β(2t)?α(1t)??β(1t)?α(2t)]=0 ?t2mβ
?2??αp??ih=?α+UTDHF(1t)?α(1t)=hTDHF?α (3-13a) ?t2m
TDHF 的单粒子哈密顿量为
2?p??h+UTDHF=TDHF (3-13b) 2m
时间有关的平均场为
?U?β?(2t)U(12)[?β(2t)?α(1t)??β(1t)?α(2t)] (3-13c) TDHF?α=∑∫d2
β
?U TDHF中的第一项是平均场的直接项,为定域势; 第二项是交换项, 为非定域势。
上述方程称为时间有关的Hartree-Fock方程(TDHF),是一组时间有关的平均场方程。求解这一方程组是初值问题(而非本征值问题),通常用迭代的方法求解,即给出t=t0的初始条件?α(t0)(对所有α=1,2,….A),通过上式计算?U(t),然后从TDHF方程计算?(t+Δt),如此迭代下去,得到任意时刻tTDHF0α0
的解?α(t)。
由TDHF方程可以证明(用迭代法证明),若初始时刻的?α正交归一,
=δαβ (3-14a) 则任意时刻的解也正交归一
=δαβ (3-14b)
即TDHF方程的时间演化保持单粒子态的正交归一性不变。
2.定态极限:HF方程
在定态极限下,令 rr?α(r,t)=e?iεαt/h?α(r) (3-15)
代入TDHF方程(3-13a),左边为
re?iεαt/hεα?α(r)
右边动能项为
e?iεαt/h?2rp?α(r) 2m
势能项中的时间因子exp[iεβt/h]与exp[?i(εα+εβ)t/h抵消后剩下exp[iεαt/h] ,两边消去这个时间公因子后,得到
?2p??)?=ε? (3-16a) hHF?α=(+UHFααα2m
??=∑d2??(2)U(12)[?(2)?(1)??(1)?(2)] (3-16b) UHFαβαβα∫β
β
这就是著名的Hartree-Fock方程。这是一组A个粒子的本征态?α和本征能量εα的非线性的自洽场方程,求解HF方程是本征值问题(而非初值问题); ?α,εα 和UHF三者要自洽确定,即(?α,εα)→UHF→(?α,εα)。
HF方程也可以从定态能量泛函变分得到( 把函数的自变量换成函数, 函数就变成泛函, 因此泛函就是函数的函数-自变量是函数)。 设多体系统的定态波函数ΦA 由A个粒子的时间无关的量子态的Slater行列式组成;这A个粒子的波r?对Φ的能量平均值泛函, 函数?(r) 是待定的。 计算HαA
?21*p?E=E[?α]=<φa|h|φa>=∑∫d1?α(1)?α(1)+∑∫d1d2?*α(1)?*β(2) 2m2αβα
U(12)[?α(1)?β(2)??α(2)?β(1)] (3-17)
考虑归一化条件,
<φa|φa>=∑∫d1?*α(1)?α(1)=A (3-18)
α
(3-17)是A个待定波函数?α的泛函(称能量泛函),求E[?α]的在(3-18)条件下的变分极值问题,即
δ?*αE[?α]=0,........δ?*α=0
或按拉格朗日乘子方法,可把约束条件(3-18)纳入泛函变分,
δ?*αI[?,ε]=0,............I[?,ε]=E[?]?ε<φa|φa> (3-19)
可得HF方程,
2?p??=(?)?=ε?. h+UHFαHFααα2m
这时, εα是作为拉氏乘子出现的。
从HF方程也可以证明,HF方程在迭代求解中,保持单粒子态?α的正交归一性,即
=δαβ
在迭代的每一步都应保持。
此外,TDHF和HF方程还保持系统的某些对称性:如系统开始时, 自洽场是球对称的,则自洽过程中始终是球对称的。
3.TDHF和HF方程的数值求解
TDHF和HF方程是非线性的偏微分方程,比较复杂,一般只能数值求解。对各类典型的物理问题,都有比较成熟的求解程序。现把数值求解的主要问题和基本步骤做一简要的介绍,以有助于大家学习与使用有关程序。
对TDHF和HF方程求解:1)首先要选取适当的单粒子态表象{ηα},这一表象能用有限数目的基矢很好的模拟(逼近)有关物理问题中平均场中的单粒子态,使得表象{ηα}的基矢的数目尽可能少,既能减少计算量,又能得到足够精确的结果。{ηα}表象的基矢最好是解析的,以简化许多积分计算。在原子物理中,通常选取类氢原子表象;在原子核物理中,通常选取谐振子表象;在固体物理中,情况比较复杂,有各种表象的选取以适合不同的情况。应当指出, 任何完备因而基矢数目无限的单粒子态表象都是平等的(等价的), 然而计算只能在有限数目的因而是不完备的单粒子态表象中进行, 这就产生了前面阐述的工作表象的选择问题。 2)表象选定以后,就要把待求的单粒子态按表象的基矢展开,把关于?α的微分(积分)方程化为展开式系数的代数方程求解。近年来,随着有限元方法的发展,人们也在坐标空间求解平均场方程;把时空离散化分成网格,然后把微分方程化为网格上的差分方程求解。无论那种解法,都要处理计算量(基矢数目)与精度之间的矛盾,巧妙的计算方法在于用尽可能少的基矢(或网格)得到尽可能精确的结果, 这就需要物理洞察力和计算经验。
求解TDHF方程的步骤是:1)给定单粒子态的初始条件?α(t0),2)计算自洽场UTDHF(t0),3)用TDHF方程计算下一时刻t0+Δt的单粒子态?α(t0+Δt),
4)重复2)、3)两步直到所需要的时刻t=t0+nΔt,求得?α(t),5)上述计算过程或者在一定表象的基矢中进行,或者在时空网格上进行。
求解HF方程的步骤:1)从物理考虑设定一组合理的单粒子本征态初值{?0α,ε0α),2)计算UHF[?0α],3)从自洽场方程计算出下一轮的{?1α,ε1α}, 与{?0α,ε0α}比较后,对{?1α,ε1α}向收敛方向作适当调整, 4)用调整后的{?1α,ε1α}重复2)、3)两步计算,一直到{?nα,εnα}与{?n?1α,εn?1α}自洽并达到所要求的精度。上述计算可以在选定表象下进行,也可以在空间网格上进行。
C.玻色子系统的平均场理论
相互作用的玻色子系统的平均场理论,可以仿照费米子系统那样建立。这时,多体系统的波函数,应当是A个粒子的波函数的乘积的对称化组合。由于波函
数的完全对称性,与费米子系统不同,同一单粒子态?α,可以填充一个以上的粒子,因而单粒子量子态?α的数目可以小于粒子的数目(对费米子系统二者必须相等)。从平均场理论求得的玻色子系统的状态一般不是系统的基态,处于较高能级的玻色子,可以向低能级状态跃迁,不管这些状态是否填充有粒子。因此,在平均场近似下,玻色子系统的基态是所有粒子都填充最低能级的玻色-爱因斯坦凝聚态。由于这个最低能级粒子数很多,可以达到宏观可观察的程度,因此玻色-爱因斯坦凝聚是宏观可观测的量子现象——称宏观量子现象,超导、超流都是这类现象。
由于玻色子不遵守Pauli原理,即使平均场产生了单粒子能级,玻色子多体系统不会产生稳定的壳层结构。因此,壳层结构是费米子系统所特有的。
D.平均场理论的意义
平均场理论是相互作用的多粒子系统的非微扰理论,是独立粒子运动模型的微观理论基础,是进一步处理量子力学多体问题的出发点。
对于费米子多体系统,平均场理论的物理后果是:
1.原子中电子运动出现壳层结构,从而导致原子化学性质的周期性。
2.原子核中的质子与中子的运动, 由于平均场存在而出现壳层结构,原子核的基态性质出现由幻数表征的周期性与稳定性。
3.对于具有规则晶体结构的固体,电子所感受到的周期性的平均场使固体中的电子的运动具有能带结构,导致固体的导电与绝缘。
因此,费米子系统的平均场理论,是原子和原子核壳层结构模型的微观理论基础,也是固体能带论的微观理论基础。下面将介绍这方面的内容。
§3-3 原子的平均场理论:原子的壳层结构[4]
A.原子中电子的运动,类氢原子和电子—电子库仑相互作用修正
从核电荷为Z的类氢原子,可以计算出电子运动的能级与波函数:
E(z)En(z)=?0
2,ψnlm (3-20) n
上式中的E0是把氢原子的E0的核电荷数从1变为Z的结果,玻尔半径自然应做相应的改变(变小)。ψnlm是氢原子波函数,但要用与Z有关的玻尔半径。
对于主量子数n,l取值为l=0,1.2,.....n?1,每个l有(2l+1)个m值,每个ψnlm有两个自旋态。所以对能级En,简并的状态数为Dn=2∑(2l+1)=2n2。由此可
l=0n?1
以计算出每个能级所能填充的电子数:
n=...1,..2,...3,.......4,.........5,..........6,..... Dn=2,..8,...18,....32,........50,........72,..
因此,略去电子—电子之间库仑相互作用以后,电子在原子中的填充按照上表形成不同的能壳,每个能壳的能量为En,电子数为Dn,这就是从类氢原子得出的原子的壳层结构图象。这纯粹是类氢原子中原子核的库仑外场对电子作用的量子力学结果,壳层结构的出现与单体势场中的独立粒子运动和泡里原理有关。然而,实际上电子—电子之间存在着库仑相互作用,它是二体相互作用,会破坏类氢原子中电子的独立粒子运动,有可能导致壳层结构的破坏。事实表明,原子的壳层
结构和由此产生的化学周期性并没有被破坏,只是有若干修改。这暗示,考虑电子—电子相互作用以后,原子中电子的单体平均场仍然近似地存在,因而需要对类氢原子的单体势场作某些修改,加进电子产生的自洽平均场。
原子中存在着平均场有以下的原因:
1)原子核(特别是Z大的原子核),提供了一个很强的外在的势场中心,即原子核的库仑场。
2)电子之间的相互作用是长程的、不很强的库仓相互作用,它们的迭加和对电子密度平均,能产生一个相当光滑的平均场,迭加在核势场之上。
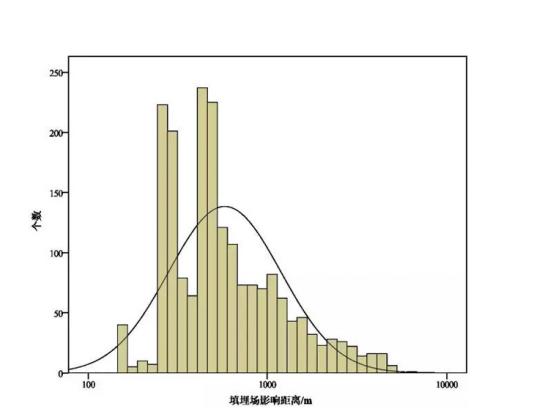
3)对基态和低激发态原子,特别是满壳外只有一两个电子的原子,由于Pauli原理的限制,满壳以下能级之间的跃迁由于Pauli原理受到完全抑制,电子之间的剩余相互作用只能导致电子向满壳外的能级跃迁。由于不同壳层之间能级差比剩余相互作用强度大,向满壳外能级的电子态的跃迁也受到部分抑制(能量标度原理)。因此, 在原子的基态和低激发态,Pauli原理的阻塞效应和壳层之间大的能级差抑制了二体剩余相互作用对平均场和壳层结构的破坏作用,使平均场仍是好的近似,壳层结构得以保持(见图3-1)。
总之,考虑电子一电子之间库仓相互作用以后,原子中电子的运动仍具有较好的自洽平均场,它迭加在原子核的库仓场之上,产生了适当修正的壳层结构。
图3-1 Pauli阻塞效应和壳层之间大的能级差抑制了剩余相互作用,
导致平均场的有效性
B.原子的平均场理论[4]
从历史上看,量子多体系统的平均场理论和壳层模型是发源于原子物理的,HF理论也是根据原子物理的需要发展起来的。
原子物理的平均场理论的特点是:1)原子核与电子相比其巨大的质量提供了一个天然的势场中心,2)核电荷(特别是Z大的核电荷)提供了一个很强的外场(库仓场),3)电子—电子之间的库仓相互作用是精确知道的、长程的,它们产生的自洽平均场导致对类氢原子势场的修正,壳层结构不会发生根本性的变化。上述特点使得原子物理的自洽平均场仅对类氢原子势场作一定的修正,壳层结构不会发生根本性的变化. 因此, 原子物理的自洽平均场理论特别成功。下面建立原子物理的自洽平均场的HF方程。
原子系统的哈密顿量为
222ZZ?pZe1ei?=∑()+∑ (3-21) ? Hri2i≠j|ri?rj|i=12μ
按照上一节的一般理论,可以得到原子中电子运动的自洽场(HF)方程,
??=ε? (3-22a) hHFααα
?为 其中单电子的哈密顿h?2Ze2?p?h=?+UHF (3-22b) 2μr
2e??(1)?(1)=∑d2?(2)[?(2)?(1)??(1)?(2)] (3-22c) UHFαβα∫β|r2?r1|βα
β
?是电子一电子库仓相互作用产生的自洽场对核势场?Ze2/r的修正。显然,UHF
求解上述自洽场方程,可以得比类氢原子的解更接近实际的解。
C.原子平均场理论的改进,能量密度泛涵方法
随着原子光谱数据精度的提高,对原子平均场理论的要求越来越高;近代的原子平均物理论已经超越了HF近似,通过能量密度泛函或平均场密度泛函的方法,不但较简便的包括了平均场的交换势,而且在不同程序上包括了HF平均场近似所忽略的多体关联效应。为了说明能量密度泛函方法,考虑平均场对密度的积分(平均场所对应的势能),
r*rrrrrrre2??UHF(r)?α(r)?α(r)dr=∫UHF(r)ρ(r)=∑∫∫drdr' ∫∑|r'?r|ααβrrrrrrrr[?*α(r)?*β(r')?α(r)?β(r')??*α(r)?*β(r')?α(r')?β(r)]
rre2rrrrrrrr=∫∫drdr'[ρ(r,r)ρ(r′,r')?ρ(r,r')ρ(r',r)] (3-23) |r?r'|rr其中,电子密度矩阵ρ(r.r')为 rrrrrrr ρ(r,r')=∑?*α(r)?α(r'), ρ(r)=ρ(r,r) (3-24)
α
r?rr这表明平均场对应的能量∫drU(r)ρ(r)可以表示成单粒子密度矩阵的泛函。更HF
一般的理论证明: 多体系统基态的能量是单粒子密度的泛函,§3-6将详细介绍这一理论。
从U=U[ρ]出发,从多体理论一般考虑和具体物理考虑,假定U[ρ]的特定形式,不但可以模拟平均场的交换势,而且可以包括一些多体关联效应,使平均场近似更臻完善。
§3-4 原子核的平均场理论:原子核的壳层结构[5]
A. 原子核中核子的独立粒子运动与幻数的存在
在量子核子动力学(QND)的理论框架内,原子核是由质子、中子组成的费米子多体系统,质子和中子统称核子;质子之间存在着长程的库仓斥力,核子之间存在着短程的核力。核力是强相互作用,总体表现为很强的吸引力,但在极小距离也表现出斥力。
与原子系统不同,原子核系统不存在大质量的势场中心。然而,令人惊奇的是,实验表明原子核存在着类似于原子壳层结构那样的幻数:当质子数Z或中子数N等2、8、20、28、50、82、126等幻数时,原子核表现得特别稳定,类
似于原子中的惰性气体。这暗示,当质子数或中子数等于幻数时,它们刚好填满一个壳层, 原子核特别稳定。在幻数上加一个核子,它的运动表现出很好的独立粒子特征,其状态可以用一个具有很好量子数的波函数来描述。按原子物理的经验,幻数、壳层结构和独立粒子运动的存在,表明原子核中也存在平均场,正是这种平均场导致独立粒子运动和壳层(幻数)的出现。
B. 原子核的平均场理论:TDHT和HF近似
对于不存在大质量势场中心的原子核,核子-核子相互作用能产生平均场的主要原因是Pauli原理和能量标度原理对剩余相互作用的抑制作用。核子是费米子,在平均场近似下,对基态原子核,核子从最低能级逐一往上填充至某一最高能级εF,这一最高能级称费米能级。质子和中子填充各自的能级,它们的费米能级一般是不同的。由费米能确定的动量空间(或其它量子数空间)的表面称费米面。对于基态原子核,费米面以下的能级全部被核子填满,对于幻数原子核,费米面以上的能级处于下一壳层,其间的能量差较大。剩余相互作用会破坏核子的独立粒子运动,引起核子从一个量子态向另一个量子态的跃迁。费米面以下的状态全部被填满,由于Pauli原理,向这些已被填充的量子态的跃迁是被禁止的;唯一可能的是向费米面以上空着的能级跃迁。对于幻数核,这种跃迁需要较高的能量,如果剩余相互作用的强度小于两个壳层之间的能量差,这种跃迁也被大大的削弱。因此,Pauli原理抑制了费米面以下核子在不同量子态之间的跃迁,而个壳层之间的能量差大和剩余作用强度小造成的能量标度不同,削弱了核子向费米面以上的量子态的跃迁。剩余作用在两个方面受到抑制,导致原子核,特别幻数核有较好的平均场和独立粒了运动。
在量子核子动力学(Qnantum Nucleon Dynamics-QND)的框架内,对于二体相互作用,原子核系统的哈密顿量可写成
2AA?p1i?=∑H+∑v(ij) (3-25) 2i≠ji=12M
这里我们已引进了同位旋τ?i,其第三分量τ?3像自旋算符σz那样具有两个不同的本征态。我们用本征值为“+”的状态描述中子,为“-”的状态描述质子,这样就把质子和中子看作同一种粒子(核子)的两种不同状态,正像电子有自旋向上、向下两种状态一样。当然,把质子与中子看作同一种粒子的两种状态只是一种近似,略去了它们某些性质(如质量)的微小差别。事实,这种处理在许多场合是r方便的、很好的近似。在这种近似下核子的坐标包括空间坐标r、自旋坐标sz和r同位旋坐标τ3(x=(r,sz,τ3))。
与电子系统不同,核子之间的相互作用(核力)是十分复杂的,目前还没有精确的表达式。因此,核力不清楚是原子核多体问题的基本困难之一。为了解决这一困难,人们有两种做法:
1.根据自由空间(真空)中核子-核子散射的数据,构造出自由空间的唯象核力,然后运用多体理论(如Brueckner理论)考虑核介质对核子一核子相互作用的修正。
2.基于核子一核子相互作用的一般性质和多体理论的一般结论,假定密度有关的等效的核子一核子相互作用,其中包括若干参数,用大量的原子核的基态性质去确定这组参数。 这类核力中最著名的叫Skyrme力,其局域相互作用为: rrrrrr vskyrme=t1δ(r?r')+t2δ(r?r')δ(r?r'') (3-26)
e和库仓相互作用。 μ|r?r'|
有了核力v(ij)之后,就可以进行原子核的TDHF或HF计算。基于Skyrme力的HF计算相当成功,可以再现大部分原子核的的基态性质。
在HF近似的基础,进一步考虑剩余相互作用中的短程对力,在准粒子近似下,可以建立起准粒子的平均场理论,即HFB理论.
C.原子核平均场理论的唯象形式一壳层模型
基于等效核力的HF近似,仍可以看作微观的平均场理论。这一理论`计算量大,一般只能得到数值结果,物理图象不够直观。为了简明直观地表现平均场理论的物理图象,人们通常选用简单的单粒子势场去模拟自洽平均场。最常用的是带自旋——轨道力的谐振子势。对球形核,平均场单粒子哈密顿量可选为
2rrr2?p122? h=+Mωr+Cl?s+Dl (3-27) 2M2
从这种单粒子哈密顿量,可以求得核子能级的解析结果。适当选取ω,C,D等参数,可以给出原子核的幻数。这种基于唯象平均场的理论,称为原子核的壳层模型,是Mayor-Jensen首先采用的核结构模型,并因此获得诺贝尔奖。
D.原子核的相对论性平均场理论
上述基于QND的原子核的平均场理论是非相对论性的,可以推广到相对论情况。因为在相对论性能量,核子—核子碰撞会产生各种介子,核子也会发生内部激发而成为一般的重子,所以相对论性原子核多体理论是必须包含介子和一般重子自由度的量子多体理论。参与强作用的介子和重子统称强子,所以描述相对论性原子核多体问题的理论框架应当是量子强子动力学(QHD-Quantum Hadron Dynamics)。QHD比较成熟而常用的理论是Walecka模型。当前在Walecka模型的框架内,已建立起相对论性的原子核的平均场理论。在这个理论中,核子按照包含自洽平均场的Dirac方程运动,平均场是由介子场产生的,而产生介子场的源又是核子的各种密度和流。这样,核子与介子场就成为一个耦合的自洽系统。
原子核的相对论性平均场理论比非相对论平均场理论取得了更大的成就,不但能解释非相对论平均场理论已解释了的所有现象,而且还说明一些前者不能说明的问题。由于相对论性平均场理论基于QHD,它使原子核平均场理论向QCD靠近了一步,成为当前原子核平均场理论研究和发展的主流。
此外, Skyrme力还包括长程Yukawa势vukawa=v0
rr?μ|r?r'|
§3-5 晶体的平均场理论:固体的能带结构[6-7]
预备知识
I.晶体:由相互作用形成的原子或离子在空间具有周期性点阵结
构的固体
原子或离子在空间的位置叫格点
晶体对称结构的最小单元叫元胞 r 元胞可用三个格矢ai(i=1,2,3)描述,格矢形成斜交系基矢
rrr元胞的体积为:Ω=a1?(a2×a3) (A1)
晶体由元胞的多次重复形成 r 晶体在格矢ai(i=1,2,3)的任意整数次平移下
3rrR=∑niai是不变的 (A2)
rr 倒格矢Ki:是与格矢基矢ai对偶的基矢,二者构成双正i=1
交系的基矢, 其定义为
r2πrr K1=(a2×a3), Ωr2πrrK2=(a3×a1), (A3) Ωr2πrrK3=(a1×a2) Ωrr由(A1)和(A3)可证:互为对偶的倒格矢Kj和格矢ai
正交归一化: rr ai?Kj=2πδij (A4)
II.晶体空间结构的对称性
晶体的对称性由其背景的周期性空间点阵结构的对称群-空间群决定
空间群(费德罗夫群):(1)离散的平移群:
晶体的离散平移群是一般空间平移变换群的离散子群:
rrrai???rT=e (i=1,2,3),a是格矢 aii
(2)晶体的点群(保持晶体一点不动的变换)是
O(3)群 [ SO(3)转动群+反射] 的离散子群。
(3) 平移群+点群:构成晶体点阵空间的空间群(费德罗夫群),它决定了自然界的晶体只能有230种晶系结构。这再一次表明了时空和背景的对称性在一定程度上决定了自然界事物的某些普通而基本的属性。
A.固体的量子力学多体问题
具有晶体结构的固体由点阵上的离子和在离子之间运动的电子组成。中性晶体的点阵离子的电荷总量等于其间运动的电子的电荷总量。晶体的哈密顿量为
?=H?+H?+V? (3-28a) HeNeN
其中电子的哈密顿量为,
2r2?1e2?=∑ H?ri+∑ (3-28b) e2m2i≠j|ri?rj|i
其中第一项是电子的动能, 第二项是电子-电子之间的库仑相互作用势能。 原子核(离子)的哈密顿量为,
2rrr?12??? HN=TN+VN=∑?Ri+∑VN(Ri?Rj) (3-28c) 2M2i,jii
其中第一项是原子核(离子)的动能, 第二项是离子-离子之间的相互作用势能。 离子与电子相互作用势能为 rr?V=V(R eN∑eNi?rj) (3-28d)
i,j
(3-28c,d) 中对离子的处理存在着复杂性和技巧: 通常把晶体上原子核外的电子分为内壳电子和外壳电子, 这种划分有一定的物理考虑和人为性; 把内壳电子和原子核作为一个整体看作离子, 仅对外壳电子进行能带论计算, 这样就可以减少计算中电子的自由度, 减少计算量, 但却增加了计算离子-离子之间和离子-电子之间的相互作用势能的复杂性; 当然, 也可以对原子核外所有的电子进行能带论计算, 这时离子就是原子核, 离子-离子之间和离子-电子之间的相互作用变得十分简单-都是库仑相互作用, 但却增加了计算中电子的自由度, 使计算量大大增加。能带论计算的物理技巧就在于恰当地定义离子和准确地计算离子-离子之间和离子-电子之间的等效相互作用。
晶体的定态薛定格方程为 rrrr? HΨα(r,R)=EαΨα(r,R) (3-29) rrr表示所有电子的坐标的集合,R表示所有原子核的坐标的集合。
B.电子运动与原子核运动的分离:Born-Oppenheimer近似。
由于晶体中原子核运动极为缓慢(慢变量),而电子运动极为迅速(快变量),因此在考察电子运动时,可以对原子核运动取绝热近似:在原子核坐标不变r&(R→0)的情况下,求解电子运动的本征方程, vrrrrrr? H0(r,R)Φn(r,R)=εn(R)Φn(r,R) (3-30a)
rrr???H0=He(r)+VeN(r,R) (3-30b) r?厄密,其本征矢组成正交完备系, 其中原子核的坐标R被看作参数。由于H0
<φn|φm>=δnm (3-30c)
rrrr固体系统的总体波函数Ψ(r,R)可以按Φn(r,R)展开, rrrrrα Ψα(r,R)=∑χn(R)Φn(r,R) (3-31)
nrα展开式系数χn(R)是原子核坐标的函数, 它描述离子的运动。把(3-31)代入 rα(3-29)式,从左边乘以<φn|,>
rrrrrr2r2ααα[∑??Ri+εn(R)+Cn(R)]χn(R)?∑Cnn'(R)χn'(R)=Eαχn(R) (3-32a) 2Miin'≠n
其中
rrrrrr2r2?Cn(R)=?Φn(r,R)|?∑R|Φn(r,R)?r+VN(R) (3-32b) 2Mii
rrrrr2
Cnn′(R)=?Φn(r,R)|∑|2?RirΦn'?r??Rri2Mi
rrrr2r2+<φn(r,r)|∑?ri|φn'(r,r)>r (3-32c) 2Miirrr上面的积分是对电子的坐标进行。Cn,Cnn'是原子核运动(用动能算符?R表示)
引起的电子运动波函数的变化(见(3-32b))以及电子运动状态的跃迁(见(3-32c))对离子势能的贡献。在绝热近似下,电子运动状态跃迁项Cnn'可以忽略,原子核(离子)的运动方程化为
rrrr2r2αα[∑??Ri+εn(R)+Cn(R)]χnμ(R)=Eαnμχnμ(R) (3-33) 2Mii
其中μ表示原子核运动中不同于量子数(α,n)的其他量子数。 (3-33)式就是晶体中离子运动的晶格动力学方程, 在谐振近似下简化为晶体点阵绕平衡点振动的声子的运动方程。
电子的运动方程(3-30a)明显写出后为
rrrrrrre22r2[∑??ri+∑+∑VeN(ri?Rj)]Φn(r,R)=εn(R)Φn(r,R) (3-34) 2mii≠j|ri?rj|i,j
这一方程可以进一步简化为束缚在原子核周围的电子的运动方程(局域电子的运动方程)和在点阵之间运动的电子(非局域电子或巡游电子)的运动方程。
C.巡游电子运动方程的平均场近似:能带结构
对于束缚在原子核周围的电子的运动,可以像处理原子问题那样,运用原子的平均场近似, 但要考虑周围电子环境和离子环境的影响;对于晶体点阵共有的巡游电子的运动的处理,是一个新问题,是本小节研究的对象。在绝热近似下,把电子运动与原子核运动分离之后,电子运动的方程仍然是很复杂的。电子受原子核的电磁作用,彼此之间又存在库仑相互作用。对于具有晶体结构一类的固体,原子核(或由它形成的离子)是作为晶体点阵骨架而周期性规则排列的。在低温情况下,它们基本上处于点阵的平衡位置而发生偏离平衡位置的微小振动。在零级近似下,可以认为原子核(离子)处于由晶体结构决定的点阵的平衡位置。它们对电子产生一个由晶体结构决定的周期性势场,这个势场原则上可以从晶体结构和点阵离子的电子结构给出。这样一来,晶体中巡游电子的运动就成为周期性外场中的库仑电子气体的量子多体问题。对这一问题的零级近似,自然是把电子看成是在周期性外场和电子自身的自洽平均场中运动的独立粒子,这就是周期性外场中库仑电子气体的HF近似,其运动方程为
2rrrr2?ψ(r)=[? h?+U(r)]ψ(r)=Enkψnk (3-35) nkrnk2mr其中U(r)包含周期性外场和电子的自洽场,而周期性外场由晶体点阵离子产生,
r其空间周期矢量Rl由晶体结构决定;在晶体周期外场的影响的诱导下,电子的
自洽场也具有相同的周期结构,因此
3rrrrrU(r+Rl)=U(r), Rl=∑Rliai (3-36)
rrrrRl??r?r=eai为基本晶格矢量。设相应于Rl的离散平移群元为PR,从晶体的周期性li=1
有,
?]=0 (3-37) ?r,h [PRl
这表示晶体中电子的平均场哈密顿量具有由晶格矢量所决定的离散的平移不变性。离散平移群是一般平移群的子群,自然也为阿贝尔群,只有一维不可约表示。 rrrrr?r的本征矢。r(r)为其本征矢,r(r)=?r(r)ur(r),r(r) 现求P设令 其中ψψ?Rlkkkkkr描述非局域性, ukr(r)(主要)描述局域性和周期性, 则
rr?rrrr?rψ(r?r?(r P)=P)Pu(r)=p(k)?(r)u(r) (3-38a) kkkRlRlkRlkr由于?kr(r)描述电子在整个晶体内的运动且具有离散平移不变性,它应是离散平
r?r的本征态,而ur(r移算子P)具有周期性,因此有 Rlkrrrr?r?(r)=?(r+R)=p(k)?(r) (3-38b) PRkklklrrrr?ru(r P)=u(r+R)=u(r) klkRlk
(3-38c) r?kr(r)的解为
rrrrrik?Rlik?r ?k(r)=e,p(k)=e (3-39a)
因此有布洛赫波函数 rrrrrrrik?r ψk(r)=euk(r), uk(r+Rl)=uk(r) (3-39b) r把ψkr(r)代入电子的本征方程(3-35),考虑到电子受离子的束缚作用,还会产生其他激发能级与量子数,故有 rr?u(r)=Eu(r) (3-40a) Hknknknk
2r2rr22r?ik2?=?+???+ (3-40b) HU(r)kk2mm2mr这表明对于一个k,电子可以很多能级Enkr。
由周期条件: rrr unk(r+Rl)=unk(r)
rrr U(r+Rl)=U(r) rr并考虑Rl与正交的波矢Km(倒格矢)的条件, rr Km?Rl=2πδml (3-41)
?r的本征矢其本征值相同: 因为 易证ψrr也是Pnk+KmRl
r=eψnkr+Kmrrri(k+Km)?runk+Km
rrnk+Km所以, 由(3-39b)有 rrri(k+Km)s?Rl?ψPrψrr=eRlnk+Km=errik?Rlr (3-42) ψnkr+Km
?r的简并态ψrr的任意线性迭加, 由(3-42)可证, PRlnk+Km~r=Cψrr (3-43) ψ∑Kmnk+KnkKmm
?r的本征矢且与ψr有相同的本征值eik?Rl, 也是PRlnk
?rψr=eik?Rlψr (3-44) PRlnknkr由于量子数(n,k)是巡游电子量子态ψnkr的完备集,具有相同量子数的态是唯一
~r=Cψr也是巡游电子本征方程的解并具有相同的本征能量。 把的,因而ψnknkrrrr
(3-43) 代入电子的本征方程(3-35),有
~r=CEEnkψ∑Kmnk+Kmψnkr+Kr=Enk∑CKmψnkr+Kr (3-45) nkKmmKmm
由于CKm的任意性,必有
Enk=Enk+Km (3-46) rr因此,Enk是以Kn为周期的连续函数。由函数论可知, 以Kn为周期的连续函数
Enk)。
1
2
k
图3-2 固体中巡游电子的能带结构
r~r(r由(3-43), 可知ψ)可有下述两种分解 nkrrrrrrrri(k+Km)?rik?r~ ψnk(r)=eunk(r)=eunk+Km(r) (3-47)
s。 代入电子的本征方程(3-35),同样得Enkr=Enkr+Kn
计算电子的平均场时,要用ψnkr或unkr去计算HF的自洽场,故关于unkr 和Enkr的本征方程是HF自洽场方程。
上述理论分析表明, 晶体的能带结构和布洛赫波的产生, 是巡游电子在晶体的周期性自洽平均场中运动的结果。巡游电子为整个晶体所共有, 它们既受离子的局域电场的控制, 又受晶体共同平均场的控制, 其运动包含局域性和非局域性两个分量, 这两个分量的竞争决定了能带的宽窄等性质: 局域性强导致窄能带, 而非局域性强导致宽能带。
D.固体平均场理论的改进
固体平均场理论的改进在两方面进行,一是选择尽可能好的表象基矢对unkr展开,以期在尽可能小的子空间内求得尽可能精确的解。由此,发展出各种解法,如正交平面波法(OPW)、赝势法、元胞法,缀加平面波法(APW),瓦尼尔表象,以及线性丸盒轨道法(LMTO-Linear Muffin-Tin Orbit)等; 这方面的改进成为固体能带论专著的主要内容。由于巡游电子的运动存在两个分量--由格点离
子束缚势场产生的在格点附近的定域分量和由晶体周期势场产生的在整个晶体内分布的非定域分量,表象的基矢也必须包含定域分量和非定域分量及其光滑连接。这是晶体平均场理论—能带论的困难之处和繁杂之处。
第二方面是改进平场势场以期更好的反映交换势并包括某些多体关联效应; 基于能量密度泛函的各种近似就属于此类。
§3-6. 平均场理论的改进:密度泛函理论与局域密度近似[8-9]
本节介绍平均场理论的第二个方面的改进: 平均场理论中自洽平均场的改进, 其目标是在平均场中尽可能多地包括非定域交换势和多体关联效应, 这是通过密度泛函理论与局域密度近似来实现的。下面介绍这方面的内容。
A. 量子多体系统基态的性质:能量最低、能量泛函对波函数变分极小
设量子多体系统的哈密顿量为
?=T?+U?+V? (3-48a) H
?, 和外场V?表为 ?,库仑相互作用U其中动能T
2r2r?1e2?=∑?=∑,...V?=∑v(r T?ri,...Ui), (3-48b) 2m2i≠j|ri?rj|ii
系统的本征方程为
?Φ=EΦ, (3-49) Hnnn
其中本征波函数Φn是正交完备的, 而本征能量从小到大排列,
E0<><><><>
{E0,Φ0}是基态,假定它是非简并的(即E0?Φ0一 一对应)。任一状态Φ'可以按{Φn}展开,
Φ'=∑cnΦn,
n=0∑|cnn|2=1 (3-50)
Φ'对应的能量泛函为, rrr?|Φ'>=<φ'|t?+u?|φ'>+drE[Φ']=<φ'|h∫ρ'(r)v(r)>
=∑|cn|2En
n
其中,单粒子密度 rrrrrrrrrrrrρ'(r)=A∫dr2dr3....drNΦ'*(r,r2,r3...rN)Φ'(r,r2,r3...rN) (3-51b)
rrr?|Φ'>=dr<φ'|v∫ρ'(r)v(r)>
显然,因为基态能量E0最低,其能量泛函的变分应为极小。事实上,设
Φ'=Φ0+δΦ',δΦ'=δ∑cnΦn,(δ为无限小量) (3-52)
n=1
E0[Φ']=E0[Φ0]+δ2∑|cn|2En, (3-53)
n=1
δE0[Φ']=E0[Φ']?E0[Φ0]=<δ∑cn*enφ*nδφ'> (3-54)
n=1
得
δE0[Φ']|Φ'=Φ=δ∑cn*EnΦ*n|δ=0=0。 (3-55) δΦ'n=10
r由于Φ0可产生唯一的ρ0(r},而基态Φ0又是非简并、唯一的,故对一个确定的r系统, ρ0(r}与Φ0之间是一一对应的, rρ0(r)?Φ0
B. Hohenberg-Kohn 定理 r 定理一:不计自旋的全同费米子系统的基态能量是单粒子密度ρ'(r)的唯一泛函。 rr?,..H?',其基态波 用反证法证明。设不同的外场v(r),v'(r)对应的哈密顿量为Hrr函数为Φ0,..Φ'0,相应的单粒子密度为ρ0(r),..ρ'0(r),其能量泛函为,
?|Φ>,..E'=<φ'|h?'|φ'>, (3-56) E=<>
?,..H?'有下列关系, 且H
??H?'=V??V?'。 (3-57) H
倘若 rrρ0(r)=ρ'0(r), (3-58)
则由真正基态波函对应的能量最小可知
?|Φ'>= <><φ'|h'|φ'>=E'+drρ(r)[v(r)?v'(r)]>E (3-59a) 000∫00
?'|Φ>= <φ0|h0rrrr?+v?'?v?|φ>=E+dr<φ0|hρ(r)[v'(r)?v(r)]>E'0 (3-59b) 00∫0
上两式相加得,
E0+E'0>E0+E'0 (3-60) rrrr这显然是矛盾的。因此,不同的外场v(r),v'(r)对应的单粒子密度ρ0(r),..ρ'0(r)必rr定不同,v(r)与ρ0(r)是一 一对应的: rrv(r)?ρ0(r)。 (3-61) r由于ρ0(r}与Φ0之间是一一对应,而Φ0决定了基态的全部性质,因此, r单粒子密度ρ0(r)是系统的基本变量,决定系统基态的全部性质。
rr定理二:基态能量E0[ρ]当单粒子密度ρ(r)=ρ0(r)时取极小值,即
δE0[ρ]|ρ=ρ0=0。 (3-62) δρrr证明:由ρ0(r)?Φ0可知,Φ0是ρ0(r}的泛函, rΦ0=Φ0[ρ0(r}]; (3-63) 由 (3-55) 知
δE0[Φ]|Φ=Φ0=0 (3-64) δΦ
可得
δE0[ρ]δE[Φ]δΦ[ρ]|ρ=ρ0=0|ρ=ρ0=0。 (3-65) δρδΦδρ
r因此, 定理二给出计算基态单粒子密度ρ0(r)的途径。
C. Kohn-Sham方程
根据上述定理,多体费米系统的基态能量泛函可表为, rrrrre2rrρ(r)ρ(r') E0[ρ]=T[ρ]+∫drv(r)ρ(r)+∫∫drdr'+Exc[ρ], (3-66) 2|r?r'|
其中,第一项是动能泛函,第二项是外场项,第三项是库仑相互作用的平均场近似下的直接项,Exc[ρ]包含库仑相互作用的平均场近似下的交换项和平均场近似下忽略了的多体关联项,它包含非定域(或动量相关)成分。剩下的问题是:(1)如何确定ρ?(2)如何确定T[ρ]?(3)如何确定Exc[ρ]?
第一、二两个问题由Kohn-Sham解决:他们假定T[ρ]可用无相互作用系统的动能泛函Ts[ρ]表示,而把修正项(包含非定域或动量相关成分)放到Exc[ρ]中去。其中 rr*r ρ(r)=∑ψi(r)ψi(r) (3-67)
i
2rrr*r?Ts[ρ(r)]=∑ψi(r)?2ψi(r)。 (3-68) 2mir这样一来,基态能量泛函E0[ρ]对ρ的变分极值问题就变成对ψi(r)在归一化条
件
<ψi|ψi>=1
下的变分极值问题:
δψ*(E0[ψi,ψi*]?∑εi<ψi|ψi>)=0 (3-69) ii
由此得
δE0[ψi,ψ*i]?εiψi=0, (3-70) *δψi
或
rr?2r2(?+VKS[ρ])ψi(r)=εiψi(r) (3-71) 2m
rr(r')δE[ρ]ρ (3-72) VKS[ρ]=v(r)+e2∫dr'+xc
|r?r'|δρ
方程(3-67), (3-71),(3-72)是著名的Kohn-Sham方程,是HF平均场方程的改进,在原子物理和凝聚态物理领域中有广泛的应用,Kohn因此获得诺贝尔奖。 剩下的问题是找出合理的Exc[ρ]。
D.Exc[ρ]的局域密度近似 其中,
知道Exc[ρ]才能求解K—S方程。Exc[ρ]是非定域的,给寻找它带来困难。r为此,Kohn-Sham对Exc[ρ]作了局域假定:假设Exc[ρ]是ρ(r)的局域泛函。 在局域泛函的范围内找出合理的Exc[ρ],需要理论的探索和经验的启示,这是运用密度泛函处理实际问题的关键。通常最简单的做法是: 对于均匀电子系统, 电子密度是常数, 容易求得其能量泛函, 然后取其泛函形式, 只是把电子密度变
成随坐标变化的局域密度。 密度泛函理论在凝聚态问题的应用和发展,都与Exc[ρ]的寻找和改进有关。这里有大量的工作成果,详细情况可参考有关文献。 E. Car-Parrinello 的从头算分子动力学(Ab Initio Molecular Dynamics) (CP-AIMD)[10]
Car-Parrinello的从头算分子动力学是一种巧妙设计的赝动力学, 它把定态本征值问题变成趋向平衡态极小值的时间有关的动力学问题。首先大胆构造下述赝动力学的拉格朗日泛函,
M&2μν2μr&i|2+∑l&ν?E0[{ψi},{Rl},{αl}] (3-73a) L=∑∫dr3|ψ+∑l22i2Ωlν
和相应的作用量
I=∫L(t)dt (3-73b) 其中, 把单电子波函数{ψi}, 形状-应力-体积等约束变量{αν}看作广义赝坐标, {μ,μν}是相应的赝惯性参数, 系统的能量E0由在一定的形状-应力-体积变量{αν} 的约束条件下的(3-66)式给出。 C-P运动方程由作用量I的变分极小给出: r*分别对ψi,..Rl,..αν变分, 就可得赝动力学方程,
δE0r+Λψ(r,t), (3-74a) ∑ikk*δψi(r,t)k
&&=??E, (3-74b) (2) 离子运动方程: δRI=0→ MlRlR0
δE&&ν=?0, (3-74c) (3 约束方程: δψI=0→ μναδαν
因为(3-74)式是二阶微分方程, 需要坐标和速度的初始条件:{ψi,Rl,αν}和
&,α&,α&i,R&ν}。 通过改变速度初始条件{ψ&i,R&ν},可以降低系统的温度T使得加{ψllr&&i(r,t)=?(1) 电子运动方程: δψ*I=0→ μψilli*r&&&&&&i,R速度(ψl.αν) 趋于零, 因而得到电子在约束条件下的定态本征方程(即带约束的电子的K-S方程和离子的平衡方程):
δE0r(1) 电子定态方程: ?+Λψ(r∑ikk,t)=0, (3-75a) δψi*(r,t)k
(2) 离子平衡方程: ?RlE0=0, (3-75b)
(3) 约束平衡方程: δE0=0. (3-75c) δαν
实际计算中, 不会完全趋于平衡. 对平衡态的偏离可以用赝动能K来度量:
M&2μν2μr&i|2+∑l&ν, (3-76) + K=∑∫dr3|ψ∑l22νi2Ωl
当K→0时, 得K-S方程的精确解。
F. 时间有关的Kohn-Sham方程[11]
在高压凝聚态物理研究中, 在高速原子碰撞中, 在超强激光脉冲与团簇相互 作用中, 电子和离子的组态会发生剧烈的变化, 描述这种动力学变化过程最可行 的近似是时间有关的平均场近似及其改进-时间有关的Kohn-Sham方程.
首先, 要把K-S静态能量泛函推广为时间有关的作用量泛函, 假定作用量泛函为
rr?1r2*rI[ρ]=I{ψiσ}=∑∫drdtψiσ(r,t)[i+?)ψiσ(r,t)?V[ρ{ψiσ}]. (3-77) ?t2miσ
作用量变分极小得时间有关的Kohn-Sham方程: r2?ψiσrr? δψ*I=0→ i={?+Uσ[ρ](r,t)}ψiσ(r,t), (3-78) iσ?t2m
时间有关的Kohn-Sham势包括离子势, 外电磁(激光)场, HF平均场和交换-关联势:
δV[ρσ]rrrrUσ[ρ]==vion(r,t)+vext(r,t)+vHF(r,t)+vxcσ[ρσ](r,t). (3-79) δρσ(r,t)
其中 rrρ=∑ρσ=∑∑ψiσ*(r,t)ψiσ(r,t). (3-80)
σσirρ(r',t)rvH=e2∫r'3 (3-81) |r?r'|
δEvxcσ=exc (3-82)
rEexc[ρσ(r,t)]是把定态的关联-交换势推广到时间有关的情况。上述时间有关的K-S方程被成功地用于描述强激光场与团簇相互作用的非线性电子动力学现象. δρσ
§3-7 散射与反应问题的平均场理论--光学模型[12]
前面讲述的是结合态问题的平均场理论,给出的单粒子态的本征能量是负的,不连续的(对晶体, 是不同能带的间断性);粒子是束缚在原子、原子核或晶体中的。对于两个多体系统的碰撞,可能发生散射或反应。这是另一类更为复杂的量子多体问题,其特征是能量为正而且可连续变化。对这类问题的处理,也可以建立碰撞和反应问题的平均场理论,作为更精确处理问题的出发点。
A.原子碰撞和原子核碰撞问题
两个原子或两个原子核发生碰撞,入射粒子(炮弹)和靶粒子都是量子多体系统,有内部结构,可以发生不交换能量的弹性散射,引起内部激发的非弹性散射,以及炮弹和靶粒子交换粒子或发射粒子、内部结构发生重组变化的反应过程。随着碰撞能量的增加,弹性散射代之以非弹性散射和反应过程,变得越来越重要。在许多情况,上述几类过程同时存在并且相互耦合。这是一个非常复杂的过程,必须借助合理近似以简化问题,才能得到一些定量的结果。幸好,无论是原子,还是原子核,其内部不同的运动模式都有各自的能标,即特征能量尺度。不同的运动模式其特征能量尺度常常相差很大,例如分子和原子核的转动,振动以及单粒子激发,它们的能标从小到大依次排列,彼此差别很大。因此,对于一定的碰撞能量E,其激发能比E大很多的运动模式就不可能激发,因而被冻结起来。因此,随着碰撞能量从小到大逐步增加,内部运动的(相应的自由度的)解冻是逐步进行的。在低能碰撞中,弹性散射和少数内部自由度(粒子)参与的反应过程是主要的,这时,平均场理论就是一个很好的近似,这就是碰撞问题中的光学模型。
B.光学模型
光学模型是建立在低能碰撞的平均场理论的基础之上的,它基于粒子作为物质波与光波的类比而引入的。入射粒子德布洛依波在靶粒子附近的传播,类似于光波在一块不均匀介质中的传播;粒子的弹性散射类似于光的折射;反应过程中入射粒子(或其特性)的消失类似于光在介质中被吸收。光学模型中的势场有实rrr部、虚部,U(r)=V(r)+iW(r);与之对应的光学介质的折射系数也有实部与虚rrr部,n(r)=nr(r)+ini(r)。 实部决定散射与折射过程,虚部决定吸收过程。这一直观的物理模型得到十分有用的结果,这一问题将在第六章中详细介绍。
参考文献:
I. 量子多体理论
1. A. L. Fetter and J. D. Walecka, Quantum Theory of Many-Particle System,
McGraw-Hill, New York, 1971.
II. Hartree-Fock理论
2. D.R. Hartree, Proc.Cam.Phil.Soc. 24 (1928)89.
3. V. Fock, Z.Phys. 61 (1930)209.
III. 原子结构理论
4. P.O.Loewdin, Quantum Theory of Atoms, Molecles and the Solid State, Academic Press, New York, 1966.
III. 原子核结构理论
5. 徐躬耦,杨亚天,《原子核理论-核结构与核衰变部分》,高等教育出版社,1987。
IV. 固体能带论
6. 谢希德, 陆栋, 固体能带论, 复旦大学出版社, 1998.
7. 李正中, 固体理论(第二版), 高等教育出版社, 2002.
V. 密度泛函理论
8. P. Hohenberg and W. Kohn, Phys.Rev. B136 (1964)864.
9. W. Kohn and L.J.Sham, Phys.Rev. A140 (1965)1133.
VI. C-P理论和时间有关的密度泛函理论
10. K. Car and M. Parrinello Phys.Rev.Lett. 55(22)(1985)2471。
11. F. Calvayrac, P.-G. Reinhard, E. Suraud, C. A. Ullrich, Phys.Reps.
337(2000)493-578; F. Calvayrac, P.-G. Reinhard, E. Suraud, Phys.Rev. B52(1995)R17506;
K. Yabana and G. F. Bertsch, Phys.Rev. B54(1996)4484;
F. Calvayrac, P.-G. Reinhard, E. Suraud, Ann.Phys.255(1997)125.
VII. 核反应光学模型
12. 徐躬耦,王顺金,《原子核理论-核反应部分》,高等教育出版社,1992。
范文二:范德瓦尔斯方程的分子平均场理论推导
第28卷第2期2009年2月大 学 物 理COLLEGE PHYSICSVo.l28No.2
Feb.2009
范德瓦尔斯方程的分子平均场理论推导
詹士昌
(杭州师范大学微流控芯片研究所,浙江杭州 310016)
摘要:利用气体分子动理论和分子平均场理论,导出了真实气体物态方程)))范德瓦尔斯方程,并与统计力学严格的理论推导结果作比较,得到了反映真实气体分子作用域大小的一个较为具体的参考值.
关键词:真实气体;范德瓦尔斯方程;分子平均场理论;作用半径
中图分类号:O441.1 文献标识码:A 文章编号:1000-0712(2009)02-0003-03
1873年,荷兰物理学家范德瓦尔斯在他的博士
论文5论气态和液态的连续性6中,提出了著名的真实气体物态方程,即范德瓦尔斯方程
p+
VM
VM-=RT
(1)
间相互作用势的简化模型球模型)作为近似,即
],
u(r)=
-u0
[2]
(仅存在吸引作用的刚
当r[r0
r0r
6
,当r>r0
(2)
式中,R为普适气体常量,VM为气体摩尔体积,a、b则分别是考虑了分子吸引力和分子固有体积影响的修正常量.在这个方程中,范德瓦尔斯考虑了气体分子所固有的体积以及气体分子间相互吸引力的影响,从而实现了将理想气体状态方程推广到真实气体情况下的修正.范德瓦尔斯当时在推导修正项a/2
VM时,所采用的是颇为简单而巧妙的唯象分子场的思想
[1]
,得到的仅是一个经验性的定性的结论,精
[2]
确的结论必须用统计力学的系统理论严格导出.
本文利用气体分子动理论和分子平均场的概念,导出了描述真实气体状态关系的范德瓦尔斯方程标准形式,得到了与统计力学方法相仿的修正常数a;并与统计力学的结论作比较,求出了反映真实气体分子吸引作用域大小的一个较为具体的参考值,这对深入理解理想气体物理模型的微观机制有重要的指导意义.
图1 苏则朗气体分子作用势模型
由图1可见,按苏则朗的分子间相互作用势的刚球模型,气体分子间相互作用势存在一个最小值,此时的分子间距离r0即为分子的有效直径,其数量级大约为10
-8
cm.当分子之间的距离r大于r0后,
分子之间呈现引力作用,但分子之间的引力作用只在一个极小的范围内存在.如果令rc表示引力存在的最大距离,则当r大于rc时,两分子之间的吸引作用微小得足以忽略不计,此rc便是分子的作用半径,其数量级约在10
-7
1 物理模型和分子平均场假设
真实气体与理想气体的本质区别在于气体分子间的相互作用力不能忽略,即真实气体的物理特性直接与分子间的相互作用直接相关.
虽然分子间相互作用势的最佳形式是1924年由列纳德-琼斯所提出的经验模型
[3]
~10
-8
cm之间.
可见,一对仅有吸引作用的刚球分子之间,其实际的作用范围为r0~rc.
图2所展示的是在气体容器壁附近厚度约为rc的薄层区域内,某一气体分子A在向容器壁碰撞过程中所受其他分子的作用情况.它将受到以其
,但在进行理
论计算时,为处理上的便捷,通常都以苏则朗的分子
收稿日期:2008-02-25;修回日期:2008-08-29
基金项目:全国优秀博士学位论文作者专项基金(:200320)、国家自然科学基金(10674039)和浙江省自然科学基金(R405097)资助项目.
)),男,,,.
4大 学 物 理 第28卷
为中心,以r0,rc为半径的半球形壳层之内所具有的其他分子如:B、C、D等的吸引作用.由于分子A的离去,必然导致它与半球形壳层作用域内各分子间所存在吸引势的增加,从而导致分子A的平均动能减小
.
根据气体分子动理论的压强公式pVM=
2
mN#3A
(7)
vT,当考虑气体分子固有体积的影响后,应有
212
pVM-=AmvT
32 综合式(6)及(7)可得232PAu0-r0p+
VM-VM
N3A
2vF2
VM-=
(8)
mvF2
进一步考虑到气体宏观温度的微观本质=
图2 A分子向器壁碰撞时受其他分子的作用情况
3R
kT,以及玻尔兹曼常量的定义关系k=,则式2NA(8)变为
2PAu0-r0p+
VM-VM
2
3
VM-=RT(9)
2
半球形壳层作用域内所具有的分子数目为
Nc=
33Prc-Pr033
NA3 rc-r0
3VM
2
NAVM
=
(3)
在上式的方括号内修正项的分母中,显然若以VM代替(VM-b)VM所引起的误差极小.为此上式可写成更简洁的形式为
a
VM-=RT(10)2
VM
上式即为描述真实气体状态关系的范德瓦尔斯方程
p+
的标准形式.
式中,NA为阿伏伽德罗常量.由于处于半球形壳层作用域内的所有分子都对分子A存在一定的吸引势的作用,即它是在这些分子所产生的平均吸引作用势场中运动的.因此,分子A与半球形壳层作用域内每一个分子的分离,都将使它有一定的动能损失$Ei,其值在0~u0范围内,作为平均场近似,不妨设
$E=3$Ei4=
u0
2
(4)
3 关于真实气体物态方程中修正常量a的进一步讨论
由上述关于真实气体物态方程的气体分子动理论和分子平均场理论导出过程可以得到,式(10)中的修正常量a为
2P23Au0rc-r09
[2]
而修正常量a的统计力学精确解为
a=ac=
23
ur3A00
(11)
2 真实气体物态方程的气体分子动理论和分子平均场理论推导
设分子A在气体中原来的运动速率为vF,由于其他分子平均引力势场的作用,当它到达容器壁表面时运动速率减为vT,根据能量守恒定律有
22
mvF-vT=Nc$E= 22
NAu023rc-r0(5)3VM2对于大量并以各种速度向容器壁碰撞的分子总体来
说,其共同效果应该对式(5)两边取平均,即
11
mvF-vT= 2(12)
比较式(11)、(12)不难看出,两个结果极其相
仿.
如果简单使a=ac,可以得到真实气体分子相互吸引作用的半径rc约为
rc=4r0=1.587r0(13)
上述关系,对于正确认识理想气体这一物理模型的适用条件,以及深刻理解该物理模型的微观机制有着极为直观和可量化的意义.
参考文献:
[] ,.[M].:
第2期
版社,1978:63-67.
詹士昌:范德瓦尔斯方程的分子平均场理论推导 5
[3] 黄昆,韩汝琦.固体物理学[M].北京:高等教育出
版社,1988:63-70.
[2] 汪志诚.热力学#统计物理[M].北京:高等教育出
版社,1980:296-303.
DerivationofVanderWaalsequationbymolecularmeanfieldtheory
ZHANSh-ichang
(MicrofluidicChipInstitute,HangzhouNormalUniversity,Hangzhou,Zhejiang310012,China)
Abstract:Byusingthemolecularmotionandmolecularmeanfieldtheories,thispaperderivesthestateequa-tionofrealgas,.ie.,theVanderWaalsequation.Moreover,incomparisonwiththeprecisesolutionaboutthestatisticalmechanics,amaterialreferencedataapplyingimplytothemolecularfunctionaryregionsofrealgasisob-tained.
Keywords:realgas;VanderWaalsequation;molecularmeanfieldtheory;functionaryradius
(上接2页)
[9] EdmondsAR.Augularmomentuminquantummechanics
[M].
2nded.
Princeton,
NJ:
PrincetonUniversity
Press,1996.
[10] LandauLD,LifshitzEM.Quantummechanics[M].
3rded.Oxford:Pergamon,1977.
SymmetrypropertiesofClebsch-Gordancoefficients
LINQiong-gui
(DepartmentofPhysics,SunYat-SenUniversity,Guagzhou510275,China)
Abstract:ThefreedomintheClebsch-Gordancoefficientsforthecouplingbetweentwoangularmomentaa-llowedbyitsdefinitionisdeterminedbytheSchurs'lemma.ThenthesymmetrypropertiesoftheClebsch-Gordancoefficientsareobtainedbyusingtheirorthonormalityandphaseconvention.
Keywords:Clebsch-Gordancoefficients;symmetryproperties;angularmomenta
范文三:伊辛模型的平均场近似是错误的理论
平均场近似对伊辛模型自发磁化的研究也是一错误的理论
马丙现
(郑州大学物理工程学院,450052)
摘要:本文分析了伊辛模型的平均场近似计算方法,结果表明:这也是一错误的数学方法,而正是这些数学错误导致了对称性的破缺,从而得出伊辛模型可以自发磁化的结论。 关键词:统计力学,伊辛模型,自发磁化,相变 PACC :0570F,0570J
The research of the spontaneous magnetization of the Ising model by the mean field approximation
method is also a wrong theory
Ma Bingxian
(Physics Engineering college, Zhengzhou University. 450052)
Abstract: This article has analyzed the average field approximattion calculation method of the Ising model, finally indicated: This also is a wrong mathematics method, and just right these wrong mathematics method causes symmetry broken , thus obtained the conclusion that spontaneous magnetization of the Ising model is possible.
Key word: The statistical mechanics, the Ising model, the spontaneous magnetization, critical phenomena
PACC :0570F,0570J
《热力学定律之殇》[1]一书指出,热力学定律是伪定律,建立在热力学定律基础之上的热力学和统计力学不是一个科学严密的理论体系,存在许多逻辑缺陷和数学错误;书中指出,虽然平衡态统计力学对计算处于平衡态的均匀系统的热力学性质时取得了一些有价值的结果,但本质上,等概率原理并不正确,不能处理相变问题。
伊辛模型是一被物理学深入讨论的模型,这一模型的求解过程之中也隐藏着统计力学本身的局限性。在《热力学定律之殇》一书第十章中,用简单对称性分析得出了没有外磁场时伊辛模型的磁矩的系综平均与温度没有关系,且总是为零;并分析了布拉格威廉斯近似推导过程的数学错误,指出正是由于其数学错误导致了对称性破缺,从而得出了伊辛模型可以自发磁化的结论。
本文将分析教科书上被广泛引用的平均场近似对伊辛模型自发磁化的研究,最后我们仍将看到,平均场近似对伊辛模型自发磁化的研究也是一个错误的理论,并且也是这些数学错误导致了对称性的破缺,从而得出了伊辛模型可以自发磁化的结论。
1.伊辛模型及其平均场近似理论[2]
设有N个自旋,处于晶格格点位置上,每个自旋只能取向上或向下两个态,并只考虑近邻之间的相互作用,这样的系统称为伊辛模型,其哈密顿量为
H=?J∑sisj?μB∑si (1)
i=1
N
其中si代表第i个格点位置的自旋,si取值为+1或?1,分别对应于自旋向上或向下。
∑
表示对一切可能的近邻对求和,J为与交换积分成正比的耦合常数。这里只讨论J>0
的情形,即只讨论铁磁情形。式(1)中第二项代表在外磁场B中的塞曼能,μ为与自旋相应的磁矩。H不再当算符处理,是一种准经典模型。
这一模型正则系综的配分函数为
Q(T,B)=
s1=±1s2=±1
∑∑"∑e
sN=±1
?H?HkT
=∑e
{si}
(2)
∑
{si}
代表对一切可能的位型{si}求和,每一自旋有两个可能取值,故位型集合(可能状态
集)中
{{s}}共有2
i
N
个位型{si}
自由能
F(T,B)=?kTlnQ(T,B) (3)
对于磁场B≠0系统磁矩的表达式可用
M=μsi=?=μ∑si==
伊辛模型的平均场理论将式(1)改写为
?F
(4) ?B
但对于磁场B=0的系统,磁矩的计算只能用一般的表达式
1
μ∑si)e?H(∑Q{si}
1?H({si})Mse{}()∑i
Q{si}
(5)
N
1
H=?J∑Jijsisj?μB∑si (6)
2i,ji=1
式中当自旋和自旋为近邻时,,否则为零;对指标独立求和而乘以因子。作用于自旋的
力为
?
?H
=μB+∑Jijsj (7) ?sij
上式右方第一项代表外磁场,第二项代表近邻自旋对自旋的作用。这种作用被看作等效
于第i个自旋受到一个等效磁场
Bi=B+
1
μ
∑J
j
ij
sj (8)
的作用。
平均场理论认为近邻自旋的取向可能不断发生变化,是涨落不定的,上式的平均值为
i=B+
1
μ
∑Jijj=B+
j
1
μ
Ji (9)
在最后一步考虑了系统的平移不变性而令j=i;z是近邻自旋数。这一理论认为i与i无关,因而认为i也与i无关,从而把上式写为
=B+
1
μ
(10)
作为平均场近似中作用于各个自旋的等效磁场。它把近邻自旋对某个自旋的作用用平均场
1
μ
代替而忽略其涨落。这样就把相互作用的自旋系统化为近独立的自旋系统。
在平均场近似下,式(2)的配分函数为
Q(T,B)=
s1=±1s2=±1
∑∑"∑e
sN=±1
N
μβ∑si
i
=∏∑eμβi
i
si
(11)
=[Z1]
其中
Z1=eβμ+e?βμ
由此计算系统磁矩为
=?
?F?lnQ?lnQ1
=kT=kTN?B?B?B
(12)
?μ?eβμ?e?βμ=Nμβμ=Nμtanh??=Nμ?βμe+e?kT?
其中
?μ?
=tanh??
?kT?
在无外磁场时,有
=tanh(βJ)
在温度降至Tc=
Jz
以下时,此方程有非零解,即体系自发磁化。 k
2.平均场近似过程的数学错误与对称性破缺
1)在系综理论中,计算系统配分函数是对系统的所有位形(微观态)求和的,系综中某一系统的能量是这一系统位型的函数,即
H=H({si})
当位形确定时,即对一确定的微观状态,任何一个格位上的自旋粒子的取向是完全确定的,因此,在系综理论中,在计算配分函数之前对处于特定位型的系统的 Bi=B+
J∑μ
j
1
ij
sj进
行系综平均或进行时间上的平均都是不合理的。实际上,如果令i=B+bi,其中
bi=
J∑μ
j
1
ij
sj,相当于其它格点对某一格点的作用用一等效磁场代替而没有平均的含义。
2)除体系处在完全有序的位形,处于一般位型的体系不具有平移不变性;同时,对不
同的位型同一格位上的i也不同,即
i=i({si})
或
bi=bi({si})
也即等效磁场是位型和格位的函数。平均场近似把处于所有位型的所有格位上的自旋粒子所受环境作用的等效磁场看成具有形式=B+
1
μ
的匀强恒定的磁场(在计算配分函数时
对不同位型不同格位按相同平均值进行计算)是完全错误的。
3)在系综理论下,考虑到系综分布对系综平均的偏离(系综理论中的涨落),可以求等效磁场的平均,由于位型集合
{{s}}和位型集合{{?s}}是同一集合,且
i
i
b({si})=
1
μ
∑Jijsj=?
jij
J(?s)=?b({?s}) ∑μ
ij
j
i
j1
H({si})=?Jsisj=?J(?si)(?sj)=H({?si})
?H{s}?H{?s}e(i)=e(i)
因而
?H{s}kT
i=∑bi({si})e(i)
{si}
=
1????H({si})?H({?si})?
bsebse+?{}()?∑i({i})?∑ii
2?{?si}??{si}?
1????H({si})?H({si})?=?∑bi({si})e?∑bi({si})e?2?ss{}{}?i?i?=0
由于配分函数求和中的各个单项是指特定的位型,因而,不能把i代入配分函数进行计算。
i已经是系综平均,在外磁场为零时,我们直接由isiμ对i求和得到总磁矩的系综平均
=∑isiμ=∑0?siμ=0
i
i
可见,总磁矩的系综平均通过等效磁场的系综平均去计算应该是零,无自发磁化。
4)数学错误导致外磁场为零时对称性的破坏 我们知道,在外磁场为零时,体系处在总磁矩大小相等而方向相反的两个可能状态上的概率是相等的;也即在没有外磁场时,可能态空间中状态对M与?M的分布是对称的。
平均场近似错误地把等效磁场写为=B+
1
μ
这一形式,导致在B=0时对任何位
型存在同一平均场=
1
μ
,从而破坏了位型集合对M与?M的分布的对称性,最终得
出自发磁化的结论。
3.通过一维伊辛模型对上述分析的说明
对有N个磁性粒子的一维伊辛模型,若满足周期性边界条件,其可能的位型图示如下:
a
b
c
d
e
f
通过图示可以看出,虽然对体系处于位型a、f时物理性质具有平移不变性,但处于另一些位型如位型d时,体系不具有平移不变性,从而得不出i与i无关;通过图示还可以看出是与位型相关的,例如:我们具体计算位型a、f
?
?Ha
=μB+∑Jijsj=μB+2J ?sij?Hf?si
=μB+∑Jijsj=μB?2J
j
?
a=B+
1
μ
1
2J (13)
f=B?
μ
2J (14)
显而易见,位型a和位型f的同一格点的等效磁场不相等,即a≠f。由这些分析可以看出,把参与平均的所有位型的系统的所有格点上的自旋粒子受到的其它格位自旋粒子的作用等效为一相同的磁场是完全错误的,即平均场理论中得出并使用=B+
1
μ
这一值去计
算系综平均是完全错误的。
在外磁场为零时,我们考虑位型a、f两个系统磁矩的统计平均: 由于
Ha=?J∑sisj=?NJ
Hf=?J∑sisj=?NJ
所以位型a参与平均的概率
1?Ea
eQ
kT
和位型f参与平均的概率
1?Ef
eQ
kT
相等
af=
1?HkT
Mae?Ha+Mfef
Q1?H (15) =Nμe?Ha?Nμef
Q=0
((
)
)
而根据平均场近似,
Ha=?μ∑sai=Jz∑sai=Jz∑(?sfi)=?Hf (16)
i=1
i=1
i=1
NNN
根据正则分布,位型a参与平均的概率
1?Ha
eQ
kT
和位型f参与平均的概率
1Ha
eQ
kT
不再相
等,其中位型f参与平均的概率远远大于位型a参与平均的概率,也就是对称性破缺,这时
Maf=
1?HkT
Mae?HakT+Mfef
Q1=Nμe?HakT?NμeHa (17) Q
1
≈?NμeHakTQ≠0
()
()
由此可见,平均场近似中自发磁化也是由于人为的数学错误造成了对称性破缺的结果,在等概率原理为基础的平衡态统计力学的框架下,正确的数学推导得不出自发磁化得结论。 4.平衡态统计理论的局限性在伊辛模型相变问题上的表现
在没有外磁场时,可能态空间中状态对M与?M的分布是对称的,而这种对称性不随温度变化而变化,现有统计理论的框架下,任何正确的理论计算都不应该得到自发磁化的结论[1]。布喇格-威廉斯近似方法(与维数无关)得到自发磁化的结论是由错误的计算引起的[1],同样本文讨论的平均场近似得到自发磁化的结论也是由错误的计算引起的,这些“错误”的本质相当于做统计平均时将对M与?M对称分布的状态集替换为对M与?M不对称分布的状态集。
不能自发磁化与实验事实不符,这些说明了现有统计力学的统计表达存在严重的问题,我们对求统计平均的状态集合的理解存在偏差。可能状态集合随宏观条件的变化而变化,相变前所使用的可能状态集合中原来等概率的状态,它们出现的概率在相变后不再相等,做理论计算时需要由描述者做相应调整。
在已有的统计理论中,一维伊辛模型为求解所做的周期性假设没有对可能态空间做本质调整,在已有的错误理论体系中是一正确结论,但与实验事实相比,和一般分析中所作的结论一样是一错误的理论结果。而与实验相符的正确结论由一些研究者以“错误理论计算”这样一种方式在不经意对参与平均的可能状态空间调整后得到。
现有物理学关于伊辛模型的讨论归结为两类:错误的理论基础加上错误的理论计算得出正确的结论;错误的前提加上正确的理论计算得到错误的结论。通过伊辛模型的讨论,我们看到依据等概率原理为基础的平衡态统计力学根本无法研究相变问题
参考文献:
[1]马丙现 2009 热力学定律之殇(郑州:郑州大学出版社)
[2]汪志诚 2000 热力学与统计力学 (北京:高等教育出版社)p380
范文四:多体理论(III)超越平均场近似地非微扰理论(可编辑)
第五章 多体理论: III
超越平均场近似的非微扰理论:
密度矩阵理论和Green 函数理论 ?5-1 纯态与混合态、多体系
统的关联等级描述[1-3] 前面两章介绍的以平均场近似为中心
的量子多体理论,都是基于多体系统的 状态用一个波函数来描述
的,而这个波函数服从薛定格方程。这种以波函数和薛 定格方程为
基础的、对多体系统的描述是量子力学的描述。本章要介绍超越量子 力学描述的量子统计力学的描述。 A (纯态与混合态 从量子统计力学的观点看,用一个波函数描述的系统的状态称为纯态,这样 的系统称为纯粹系综。在一般情况下,一个量子系统需要用几个或一系列波函
数 ,ψ ,ψ Lψ??? 来描述,每一个状态以一定的几率w w w , L ???出现,但它们不 1 2 n
1 2 n 能迭加产生一个新的量子态,这样的量子状态称为混
合态,这样系统称为混合的 系综。 如把一个量子系统放在一个热
槽中,由于受热槽的影响,这个系统的本
E ?kT 征态, E ψ 会以 n 的几率出现,这些几率w 不是由量子力学定律决定 w e ? n n n n 的几率,而是由
统计热力学定律 所谓正则系综 决定的几率,因而是经典
性的 的几率。 对于混合系综,前面两章描述纯粹
系综的量子力学方法显然是不够的,必须 寻求新的描述方法。本章
介绍的密度矩阵理论和 Green 函数理论正好适合对混
合系综的描述. 因为纯粹系综是混合系综的特例 (w0 1 ,
其他wn 0 ),密度矩 阵描述和 Green 函数描述自然也适
合描述纯粹系综,因而与使用波函数的量子 力学描述是等价的。
B (多体系统的关联等级理论[3] 除了适应描述混合系综即量
子统计力学的需要外,发展密度矩阵理论和 Green 函数理论还有别
的原因。其中之一是,这两种理论都蕴含着按粒子数从少 到多的关
联等级描述的可能性。前面已指出,剩余相互作用要破坏粒子的独立量
子运动,造成粒子间的关联。这种关联按粒子数多少有二体关联,三体关联直至
n-体关联等不同等级的多体关联。密度矩阵理论和 Green 函数理论能很好地描
述 粒子之间因相互作用、相互影响而形成的多体关联,而且能发展
成为描述各个不 同等级的多体关联的关联等级理论,在适当的等级
截断之下,它不仅包含平均理 论,而且还包含各种高阶关联的非微
扰理论。这正是处理强耦合系统所特别需要 的,因而具有特殊的吸
引力。 ?5-2 密度矩阵理论:多体关联密度矩阵动力学[2,3]
A (密度矩阵与冯-诺意曼方程 考虑具有二体相互作用的费米
子系统,其哈密顿量为 A 1 A + ? ? ? ? H h i v ij
+ ,H H 5-1 ?
? 1 2 ? i i j 1 ?h2
2 ?
h ? + U r 5-2 2m 而与时间有关的多体薛定格方程
为 ?ψ A x ? ih H x ψ A 5-3a ?t 其共轭方程为 * ?ψ A'
x ′ ? ′ * ?ih
H x x ψA 5-3b ?t x 5 3 a ×5 3? b 由?ψ ? x ? × ψ ′ 得 A
A , x
x ′ ?ρ
A ? ′ ′ ?
H x x x i x x H x h , ρ , ρA ? A ' 5-4 ?t 式 5-4 称为冯-诺意曼方程,是A 个粒子的量子系统的密度矩
阵 ,x x, t xt x
t ′ ? ′ ρ
ψ ψ
5-5 A A A ′
?
,xρx, t ρ 所满足的运动方程。 A 是密度矩阵算符(统计算符) A 在坐标表象的矩 阵元, 其中 是矩阵的行列指标, 与通常矩阵
的行列指标不同的是他们取连 ,
x' x 续值。密度矩阵写成算符形式后,冯-
诺意曼方程也可简练地写成算符形
式 ?
?ρA ? [? ? ? ? ] ? H ?ih Hρ L ρ ρ 5-6 A A H
A ?t
? ?
? ρ LH 是对应于H 的冯-诺意曼算符 或
量子刘维算符 , A 用 Dirac 符号的抽象表示 为 ?
| ρ |ψ ψ 5-7 A A A 在 X~表象中的矩阵元为 ,xρ'x,
t ? ′ ′ ? ′
| | x | xψ xψ| ρ 5-8 A A A A A A
ψ x ′ 可证冯-诺意曼方程(5-4 )与薛
定格方程 5-3 等价: 以 A 右
乘(5-4 )并对 ′ d dx 积分得(用到归一化条件不变,
ψ| )
A A dt ? ? ?
? ?
, H i | x t |ψψ ψ ψ ψi |
|ψ , H x t h ? ? A ? A A A A
A ? ?t
? ?t ?
? ?
ψ,x t ψ,x t
ψ,x t 由于 A 的任意性,算子
ih ?H 作用在任意的 A 上还等于 A
是
?t
? ? 不可能的,因此,必有 i
hH ? xt 0ψ ,方程才能成立。这就从冯-诺意
曼
方 ?t 程得到薛定格方程。(也可从规范变换来论证)
冯-诺意曼方程可以推广到混合系综的情况,这
时, ? & ρ| ψ w |ψ
w 1, w 0 5-9 ? ? A n n n n n n
n ?? ρA ? ? ? ? ? ?
H ih H ρ L ρ
ρ ? A A
H A
5-10 ?t 其中 ? H | E |ψ ψ ψ |ψ δ
5-11 n n n
n m nm 冯-诺意曼方程 5-10
右乘以|ψ 消去公因子w 后,得 n n 2 ? ?
w ? ?
m ?
?
?
ih H | ψ ψ ψ |ψ ψ| | ψih ψ
| | H |
? ? n ? m m n n n
n ? ?t
w ?t
? m
n ? 同样的理由导致 ? ? i h| ?H 0 ψ ?t
n 由于混合态的分布几率w
是外部引进的、与时间无关的,冯-诺意曼方程描述的 n
?
是混合系综的动力学演化, 即由ψ x,t )的量子
动力学演化引起的ρ t 的动力 n
A ?
学演化。在ρA 中 ψ,x t 是量子力学动力学量,而w
是外来的统计量。 n n B、约化密度矩阵及其运动方程
引进 n-体约化密度矩阵 1 ′ ′ ′
Tr ′ ′ ′
12 1Lnn;1 2LA L1 nρn LA + +
12 ;1 2 Lρn Ln A n
n1... A+
A !n ? 1 ' ' dx dx x x x x x Lx x ... Lx L
ρ L ; 5-12 ? n+1 A A 1 n n +1 A 1 n n +1 A
A !n ? 其中 Sp tr 求迹运算, 包括对连续
变量的积分和对不连续变量的求和。令单粒 子
一体 密度矩阵 , x x ,ρx x ′
ρ ′ , 1 其对角元素 表示多体系统在 x 点的粒子密度; 二体密度
矩阵ρ 的对角元 ,ρx x 2 x;x ρx x 表示粒子在x 和x
点出现的联合密度,其余以此类推。从 5-9 式 2 1 2 1
2 1
2 ? 可见, ρ 的对角元出现的量子力学波函数的相位角由于波函复共轭运算正
好相 n 消, 只有 ? ρ 的非对角元体
现出多粒子系统的量子力学波函数的全部信息: 相位 n 和振幅,包含着物质波的相干性信息。因此,
量子力学波函数作为物质波的动
力 ? 学信息主要包含在ρ 的非对角元之中,它们真正体现出量子力学关联。 n 对ρA 的运动方程求迹,可以得到ρ
的运动方程, 它们是:
n 一体密度矩阵运动方
程: ?ρ ′
11
[? ′ ′ ′ ? ] ′ ′ ′ ′ ′ ′ i h h ? Tr v + ? v 1 1 12h 11 12ρ,1 211 ρ
12,1 2 1 2 [ ρ2
ρ2 ] ?t
2 ?
, h] ρ [ Tr+, [v ]ρ 2 5-13 2
二体密度矩阵运动方程: ?ρ2
[? ? ] [ ] + 2 , + ih h 13+ h1 23Tr , v ρ v ρ
5-14 2
3 ?t 3 …………………
n-体密度矩阵运动方程: ?ρn ih .......... 5-15 ?t 上述ρ 的运动方程叫BBGKY 系列,是链条式的耦合的非线性的运动方程组系 n 列,与冯-诺意曼方程等价;但它优点是, 把
描述多体系统的总体性质ρA
的运动 , ρ , ρ ρ
Lρ 等一系列部分粒子集团的性质的运动方程,ρ
方程,分解成描述 1 2
3 n
n 所描述的 n 个粒子集团子结构正好包含量子
多体系统的 n-体关联。BBGKY 系列 的缺点是
没有提供一个合理而系统的截断方案,因而这个众多(几乎无限)的运 3 动
方程组系列不能截断求解。克服这一缺点的努力导致关联密度矩阵动力学的建 立。 C(多体关联密度矩阵动力学[3-5] 对约化密度矩阵ρ 作集团展开: n
n?1
ρ ASρ ρ +C c ρ ρ
5-16
n ?n pp? n 1 1 p 1
其中Cn 是 n 体关联, A 是反对称化运算, S 是对
称化运算。 以ρ2 为例, 有
12,1 2 11 22 12,1ρ2 ′ ′ ASρ
ρ′ ′ +C ′ ′
2
2
′ ′ ′ ′ ′ ′
5-17 .................. 11 22 12 21
ρ 12,1 2ρ ρ ρ ? +C2 c ρ 通过集团展开, ρ 的运动方程就变成C 的运动
方程 (其中1 ) n n & i h Tr v AS[ , ]
Cρ +[ , ρ ρρ+ ] h 2
5-18
&
h i C h h C v AS C Tr v[ 1 v 2 ,
AS] [+, ] + [ + +13 ρρ 23 ,+ ρρρ +ρ
C+ C ] 2 2 2
2 3 L 5-19
………………………………………………………… &
h
5-20
i C ........................... n 其
中[.....] 表示连接项,该项中每个函数因子中的变量是重复相联的(对应于
场
L 论
中连接的 Feynman 图形)。 上述方程构成了关联密度矩阵动力学的基本方程,其特点是: 1(从ρ 中分离出连接的部分,像场论中的不可约连接图形,避免了信息的 n 重
复; 2 (是非线性的耦合的运动方程, 既体现各阶多体关联
的相对独立性, 又体现 出它们之间的耦合与关联; 3 (因为多体关联C 随 n 的增加而迅速减小,上述方程组本身
提供了一个自 n 然
而合理的截断方案; 4 (对每一种截断近似,都导致一组封闭的非线性非微扰的耦合的运动方程。 D 、二体关联密度矩阵动力学及其应用 二体关联密度矩阵动力学方程组由假定三体以上的关联为零而得到,它们是
h& i h T v [AS, ]
C[ρ 12+ , ρ ρρ+ ]
5-21a r 2 & i C h h C v AS C T[ v 1
2v , ]ASh[ 12+ , ] ++[ +13 ρρ 23 ,+
ρρρ ρ + C ] 2 2 2 r
2 L 5-21b
这是耦合的、非线性的、非微扰的、包含ρ和 C2
的封闭的运动方程组,是超越 平均场近似 TDHF 的运动方程,已获得广泛的应用。 1. 平均场近似:TDHF 和 HF 令C 0,从二体关联密度矩阵动力学方程得到平均场近似的方程, 2
& i [h , ] T [v
12 ,AShρ +] ρ r ρρ
5-22
这是密度矩阵形式的 TDHF 理
论。
?
ρ
因为 是厄密的,可以通过幺正变换对角化,在其本征表象
中,
? | ρ ψ n |ψ 5-23 α? α α α 4 填充状态|ψ 的几率n
满足, α
α n A ,.......?0 n ? 1 5-24 ? α
α α
|ψ 是正交、归一、完备的单粒子态,
α ψ ψ δ ψ ,.... ψ ||
| I 5-25 α β αβ ? α α α ? 显然|ψ 是ρ 的本征态,其本征值为n
α
α ? ρ ψ| ψ ψn |ψ | | δ n ψ | n
ψ 5-26 ? ′ ′ ′ ? ′ ′ α α α α α αα α α ' α
α ′
′
α α
一般情况下,0 ? 1 ?n ,因此 α ? 2
2 ? | | | ψ|
ρ|| | ψ n ρ ? | 5-27 ? α
α x α
TDHF 近似为独立粒子近似,每个粒子有确定的量子态,即填充几率必须为
n 1或 0, α
这样 ? ?
2 ?1, 填充 ? ρ ρ nα ? 5-28
0, 不填
充 ?
? 因此,TDHF 的ρTDHF 为 ?
|ρ ψ |ψ 5-29 TDHF ? α
α
α ? ? 把ρTDHF 代入ρ 的运动方程,按照从冯.诺意曼方程到薛定格方程类似的推
导,可
得 ?ψα ? ? ih h+ U TDHF ψα
范文五:相对论平均场理论对重核中结团现象的研究
第30卷增刊Ⅱ2006年12月
高能物理与核物理
HIGH
ENERGY
PHYSICS
AND
NUCLEAR
PHYSICS
Vol.30,Supp.Ⅱ
Dec.,2006
相对论平均场理论对重核中结团现象的研究
王士虎
1)
郭建友
合肥
230023)
(安徽大学物理与材料科学学院
摘要用相对论平均场理论结合结团模型对重核结团现象进行了研究.首先将原子核分为两个部分,然后用相对论平均场模型对原子核的核子按束缚能的高低来分布,结果获得了与实验相一致的结团.这表明相对论平均场模型也适用于重核结团现象的研究.关键词相对论平均场重核结团
1引言
重核结团的研究中占据很重要的地位.自从
[1]
2理论框架
相对论平均场理论(RMF)
[15,16]
是一个相当成功
Sandulescu等预言重的结团自发裂变以来,人们陆续发现了很多重的结团自发裂变现象(14C,
28
20
[2]
的理论,它解决了原子核领域的很多难题,我们在这里同样是用它来解决重核结团的.首先,我们给出相对论平均场理论(RMF)的拉格朗日密度:
L=iγμ?μ?m?gσσ?gωγμ?gργμτρμ?
?
O,
24
Ne,
Mg,
32,34
Si···),导致了对重结团结构的关注.目
[4]
[5]
[3]
[15,17—20]
前人们建立了许多结团模型,如统一模型,超非对称裂变模型分析(ASAFM),有效液滴模型(ELDM),密度依赖的结团模型(DDCM)
[6—11]
等.
[12]
除此之外,人们建立了既包括结团的描述又包括平均场的描述的费密子的分子动力学方法(FMD)反对称分子动力学方法(AMD)等
[14]
[13]
1?τ11μ32eγμAμΨ+?σ?μσ?m2σσ?222111
g2σ3?g3σ4?ωμνωμν+344112μ
mσωωμν+c3(ωμωμ)2?241μν11μρρμν+m2ρμ?AμνAμν,ρρ424
?
,
等,也已经可以很
好地解决轻核结团结构的模型.最近,P.Arumugam
用相对论平均场模型(RMF)给出的分布密度也对轻核结团结构给出了一个清晰的物理图象,并且与实验结果很好的符合.但是,由于有些重核中存在较强的自旋–轨道耦合,他们无法用由相对论平均场模型(RMF)给出的分布密度得到这些重核中的结团结构
[14]
(1)
其中Ψ是核子的Dirac旋量,对应的质量为m.ω和ρ分别是isoscalar-scalar和isoscalar-vector介子.σ是isovector-vector介子.光子场A提供了原子核中的电磁属性.相关张量如下:
ωμν=?ων??ωμ,Aμν=?Aν??Aμ,
ρμν=?ρν??ρμ?2gρρμ×ρν,
μ
ν
μ
ν
μ
ν
.
本文根据结团放射性的理论中的一些基本假设(原子核分成子核和结团两部分,这两部分与单个原子核具有相似的物质密度分布)
[6—11]
将原子核分成了内(2)(3)(4)
外两部分,利用相对论平均场模型(RMF)对这两个部分结合能进行了计算,很自然的导出了重核结团结构.通过对目前已知的大部分具有重核结团放射性的重核进行计算,发现与实验符合的比较好.
将拉格朗日密度代入Euler-Lagrange方程,我们很快得到核子的场方程.由于我们只涉及到原子核的基态
1)E-mail:wshihu@yahoo.com.cn
87—89
88高能物理与核物理(HEP&NP)第30卷
性质,我们可以设介子场和光子场是静态的经典场,核子在经典场中做独立运动.
3
计算细节
对于参数的选择,我们对原子核采用了较好的
符合重核性质的一组参数NL3.值得注意的是,对关联对重核的定量计算是十分重要的,所以我们采用了简洁而有效的固定能隙的BCS(Barden-Cooper-Schrie?er)方法处理对关联:?=12
.将对相互作用
作为微扰项,对不成对的核子采用泡利阻塞的办法处理.在这里,我们采用变形轴对称谐振子基展开的办法(主壳Nb=Nf=20),参数β2由核电四极矩Q给出.这里的Q为
Q=Qn+Qp=
9
5π
AR2β2,(5)
其中R=1.2A1
fm,输入的形变参数β的初值选取任意合理的值.
我们以如下方式考虑要解决的问题.先假设将某个原子核分成两部分,则这两部分应可视为两个新的独立的原子核(当然这时原子核不一定稳定)
[6—11]
.由
于原子核之间是弱关联而原子核内部是强关联,所以两个原子核之间的作用对于原子核内部的强关联而言只是微扰.而任意系统在无外界能量激发下基态的粒子总是向更高结合能处迁跃,所以两个新原子核的最外层核子的迁跃运动仅仅取决于两个原子核最外层结合能的高低.当任意一个原子核的最外层不再俘获或失去核子时,两个原子核就稳定了.此时,比较小的原子核就应该是分裂出来的结团.而原子核内部的结合能可以根据相对论平均场模型(RMF)计算,所以我们用相对论平均场模型(RMF)可以算出这2个原子核的核束缚能(大核用形变核计算,小核用球形核计算).由此可以确定可能出现的结团以及结团的结构.更复杂的问题也能依此解决.
为简化问题,实际计算中可以先假设分裂出一个质子.又由于对力的存在,2个核子在一起时的结合能比单个核子高,因此实际计算中考虑以2个核子为一个基本单位:
S2p=EB(Z?2,A?2)?EB(Z,A),(6)S2n=EB(Z,A?2)?EB(Z,A),
(7)
其中EB(Z,A)是质子数为Z,质量数为A的核束缚能.与此同时,我们还将实验所得出的结合能与之进行了
比较.
4
结果及讨论
我们知道结团要形成,必须它本身比较稳定.中
子数目的范围随质子数而定,而质子数是可以连续变化的.所以,为了减少计算量我们首先来看看中子数随质子数改变的情况.由于纵坐标是能级差,所以当某一点为负值,而它的右面为正值时该点代表的结团既不俘获新的核子,其最外层核子也不被别的核俘获(注:由于每个原子核里都有4He结团,所以有些原子核省略了,纵坐标的值是大核最外层中子或质子的结
合能减去小核最外层中子或质子的结合能).
图1
Numericalrelationsbetweenneutronsandprotonsinsmallparts——
224Ra.
图2Numericalrelationsbetweenneutronsandprotonsinsmallparts——224Ra.
从图1,2可知,224
Ra中有4He结团(这点我们在
其他原子核的分析中可以看到,因为每个原子核都一样,所以我们省略了)还有18O?4He=14C结团.其中,我们注意到16C对最外层的两个核子的束缚极极小,
增刊Ⅱ王士虎等:相对论平均场理论对重核中结团现象的研究89
在小结团受到大结团作用时(该作用相对结团内部作用来说极小)会失去两个中子.所以就不考虑20O时最外层质子的情况.
子核的结构获得更深入的了解.由于本理论只涉及到结合能的计算,在具体应用中几乎不存在限制条件.
但是,我们也注意到某些核子的分析结果与实验存在一定差距.这有可能是由于原子核衰变时使α结团发生了分裂,也有可能是由于(RMF)的误差.该理论的成功说明考虑了BCS的RMF可以对重核的结团结构作出较好的描述,这也为结团现象的研究开辟了一条新的途径.
5结论
我们通过以上分析可以看到大部分本文所讨论的
原子核都符合重核的结团放射性实验的数据.更进一步得到了重核内部的结团结构.这样,我们可以对原
参考文献(References)
1GreinerW.Z.Phys.,1994,A349:315
2SandulescuA,PoenaruDN,GreinerWetal.Sov.J.Part.Nucl.,1980,11:528
3RoseHJ,JonesGA.Nature(London),1984,307:2454PoenaruDNetal.Z.Phys.,1986,A325:435
5DuarteSBetal.At.DataNucl.DataTables,2002,80:235
6XUChang,RENZhong-Zhou.Phys.Rev.,2003,C68:034319
7XUChang,RENZhong-Zhou.Phys.Rev.,2004,C69:024614
8RENZhong-Zhou,XUChang,WANGYong-Qinetal.Nucl.Phys.,2004,A738:318
9XUChang,RENZhong-Zhou.Nucl.Phys.,2005,A753:174
10XUChang,RENZhong-Zhou.Nucl.Phys.,2005,A760:
303
11RENZhong-Zhou,XUChang,WANGZai-Jun.Phys.Rev.,
2004,C70:034304
12FeldmeierH,SchnackJ.Rev.Mod.Phys.,2000,72:65513Kanada-En’YoY,HoriuchiH.Prog.Theor.Phys.,2001,
142(Suppl.):205
14ArumugamP,SharmaBK,PatraSK.Phys.Rev.,2005,
C71:064308
15SerotBD,WaleckaJD.Adv.Nucl.Phys.,1986,16:116SerotBD.Rep.Prog.Phys.,1992,55:1855
17GambhirYK,RingP,ThimetA.Ann.Phys.,1990,198:
132
18SugaharaY,TokiH.Nucl.Phys.,1994,A579:55719PandaPK,PatraSK,ReinhardtJetal.Int.J.Mod.
Phys.,1997,E6:307
20GmucaS.Nucl.Phys.,1992,A547:447
RelativisticMeanFieldStudyofClusteringinHeavyNuclei
WANGShi-Hu1)
GUOJian-You
(DepartmentofPhysics,AnhuiUniversity,Hefei230039,China)
AbstractTheclusteringphenomenoninheavynucleiisdiscussedinthispaperwithintherelativisticmean?eld(RMF)approach.TheclusterscanbeobservedinexperimentsareobtainedthroughthecalculatednucleonbindingenergydistributionsaccordingtotheRMFtheoryaftertheatomicnucleusisdividedintotwoparts,insteadoftheusualmethodofanalysistothecalculatednucleondensitydistributionsbecauseofthestrongerspin-orbitcoupleinheavynuclei.TheresultsindicatethattheRMFtheoryiswellsuitedforthestudyofclusteringinheavynuclei.KeywordsRMF,clusteringinheavynuclei
1)E-mail:wshihu@yahoo.com.cn



 秋心伊始
秋心伊始

