利用等厚干涉测金属细丝的直径

范文一：利用等厚干涉测金属细丝的直径

利用劈尖干涉测定细丝直径

09物理学: 罗有仁谢青春王晶

指导老师:王兴华

摘要: 干涉和衍射是光的波动性的具体表现。等厚干涉又是光的干涉中的重要

物理实验。而作为等厚干涉的具体应用—— 利用劈尖干涉法测定细丝直径 ,是

一项很好的设计性实验。

关键字: 读数显微镜;钠光灯;空气劈尖;等厚干涉;条纹一、实验目的

1、观察了解等厚干涉的原理和现象;

2、进一步学会使用读数显微镜;

3、学习用等厚干涉测细丝的直径。

二、实验仪器

读数显微镜、钠光灯、空气劈尖

三、实验原理

设细丝直径D，空气劈尖的长度L，则X处第K级暗纹产生的条件为 D

,,, (=0、1、2…) ,2，，21,e，,，,,

22X 第K级暗纹(即从顶点算起，第几条暗纹)对应的劈L

图一:等厚干涉原理尖厚度为

, (1) e,k

, (n取1) (2) ,D,n

x相邻暗条纹间距 (3) ,x,

eD由图二可知，相似比 (4) ,

,L由(1)、(3)、(4) (5) ,D,,

,x2

K条 D D N条 e N条 D , x

图二 L

图三图四

,L若劈尖中段N 条暗纹长度为， ,D,N,

,2x

,L 则 (取N=60) (6) D,N,

22,， (7) u(L)(L)(L)uuBA

22,， (8) u(l)((l))((l))uuAB

22,D,D (9) ,，u(D)(u(L))(u(l))

,L,l

四、实验内容及要求

1、点燃钠光灯，将由待测金属细丝和玻璃片所组成的空气劈尖置于显微镜下平台P上，调钠光灯使入射光经,45半反镜G反射后投射到劈尖N上，再由N反射经G进入显微镜。应保证有足够的光强反射到显微镜中。

2、仪器调整

(1)调视度。旋转目镜，使叉丝成像在目镜平面上，此时叉丝最清晰。

(2)调视差。目测，用调焦手轮将显微镜筒下移至接近劈尖处，在缓慢升起镜筒，使劈尖干涉条纹成像在物镜焦平面上，此时在目镜中看到的条纹最清晰。 (3)使整个劈尖位于显微镜的移动测量范围内，且干涉条纹与叉丝平行。

3、实验测量

(1)测。移动显微镜，使竖叉丝对准视场中清晰暗纹，每隔60条读取一次坐l

标，则为两次相邻坐标差，共测6组。 ,

(2)测。移动显微镜从劈尖第一级暗纹(与棱边重叠，并含与其中)到细处，L

读取两端坐标，则为两坐标差，共测5组。 L

4、数据记录

计算、L、d的平均值及D的总不确定度、相对不确定度，并表示实验结果。 ,

,7利用劈尖干涉法测细丝直径用表 mm (5 893 ,5) ，10,,

单位mm 棱边的位置细丝的位置 xxxx0Nnn，bNxx,,n，bnxxL,,N0l1 14.511 25.562 40.119 60 2.381 42.500 11.051 2 16.641 27.038 40.111 60 2.218 42.329 10.397 3 18.650 28.427 40.108 60 2.379 42.487 9.777 4 20.531 29.762 40.096 60 2.223 42.319 9.231 5 22.312 31.050 40.090 60 2.385 42.475 8.738 平均 40.1048 60 9.8388

5、数据处理

S(L),0.0117mm,40.1048mmL

,L D,N,,0.07206mm

,S(L)

(L),S(),,0.005228mmuLA

0.004,0.00231mm, (L)uB3

22,，= u(L)(L)(L)0.007786mmuuBA

S(l),0.0.917335mml,9.8338mm

,S(l)

(l),S(),,0.41024mm ulA

0.004,0.00231mm, (l)uB3

22= ,，u(l)((l))((l))0.16833mmuuAB

,DN,NL,D,,3,3,, ; ,,,,1.797，10,7.32，10

lll,2,L2l

22,,DD,3 ,，,mmu(D)(u(L))(u(l))1.23，10

,L,l

实验结果报告:

金属细丝的直径: D,(0.072,0.001)mm

四、注意事项

1、钠光邓波长,=589.3nm。电源接通后，要等实验完成后再关，以免频繁开光

损坏钠光灯。

2、读数装置读数方法与千分尺相同，=0.004mm ,仪

3、回避空程误差。移动显微镜要缓慢，切不要移过头再返回对准，以免产生空

程误差。测,时，要沿一个方向测好所有数据，显微镜中途不要回头。 4、视差调整中，显微镜筒必须是自上而下移动，不能上下调整，以免碰坏物镜

与劈尖。

五、测量方法研究与误差分析

(1) 靠近细丝附近 ,由于条纹偏密 ,测得的条纹间距偏小 ,则测量值 D 偏大。 (2) 靠近棱边处 ,由于劈尖制作不够规范 ,导致干涉条纹粗而弯曲 ,使测得的条

纹间距偏大 ,从而造测量值 D 偏小。

(3) 在棱边与细丝之间选一段清晰的直条纹进行多次重复性测量 ,可以减小测量

误差，但这样做人为因素影响较大。

(4) 在棱边与细丝之间 ,尽量靠近棱边一侧 ,在条纹清晰 ,平直的较长区域内 ,

连续测量多组数据。

(5)因为测量细丝直径的实验公式 ,是在忽略入射角对光程差影响的近似条件下

导出来的 ,并且又仅适用于等间距的干涉条纹。而在实际测量中干涉条纹间

距不相等 ,这样就造成理论上的系统误差。

六、参考文献

[1]赵凯华,钟锡华.《光学》上册,北京大学出版社,1982.

[2]赵凯华,钟锡华.《光学》下册,北京大学出版社,1982.

[3] 杜义林.《实验物理学》,中国科技大学出版社,2006.

范文二：细丝直径的测量

细丝直径的测量

摘要：本次实验为细丝直径的测量，由于细丝利用普通的测量工

具很难准确测量，误差很大，所以此次实验是利用等厚干涉原理，即由同一光源发出的平行单色光垂直入射分别经过空气劈尖所形成的空气薄膜上下表面反射后，在上表面相遇时产生的一组与棱边平行的，明暗相间，间隔相同的干涉条纹，由此来测量细丝的直径，使数据更加准确，本次试验就是利用干涉原理制作劈尖测量发丝的直径。

关键词：干涉原理空气劈尖直径光程差

引言：本次实验是利用空气劈尖根据光的干涉原理测量发丝的直

径，干涉和衍射是光的波动性的具体变现，利用光的等厚干涉由同一光源发出的平行光，分别经过劈尖间所形成的空气薄膜上下表面反射后产生干涉现象，形成明暗相间的条纹，使用显微镜观察明暗条纹间的距离，由此来计算发丝的直径

实验原理：

当两片很平的玻璃叠合在一起，并在其一端垫入细丝时，两片玻璃片之间就形成了一层空气薄膜，叫做空气劈尖。在同一光源发出的单色平行光垂直照射下，经劈尖上下表面反射后将会产生干涉现象，在显微镜观察可发现明暗相间的干涉条纹，如图所示

实验内容与步骤：

实验仪器：读数显微镜 45度反射镜 2片光学玻璃钠光灯发丝 1 将发丝夹在2片光学玻璃的一端，另一端直接接触，形成空气劈尖。将劈尖放在读数显微镜的载物台上。

2 打开钠光灯，调节45度反射镜，使光线平行垂直射入充满视野，此时显微镜的视野由暗变亮。

3 调节显微镜物镜的焦距使视野内明暗相间的条纹清晰，调节显微镜目镜焦距以及叉丝的位置是否对齐和劈尖放置的位置，

4 找出一段最清晰的条纹用读数显微镜读出两条明条纹或暗条纹之间的距离，同一方向转动测微鼓轮测量出5组明或暗条纹的间距。 5 使用游标卡尺测量出劈尖内细丝到较远一端的距离L 6 根据公式和测量的数据计算出细丝的直径和不确定度

数据处理与实验结果表达式：

S=(0.212+0.220+0.216+0.218+0.220)÷5=0.2172mm L=45.2mm D=?=

L λS 2

45. 2

0. 2172

589. 3?10

-6

=0.061mm

U l =0.01mm

U s =t

∑(S

n =1

-S ) 2

n (n -1)

=2.78?0.00665=0.0185

U l 2U S 2

U r =() +() =0. 00029=0.017

L S

U D =D ?U r =0.013?0.017=0.0221 最后结果为

D=D ±U D =0.061±0.0221mm U r =

U D D

?100%=1.61%

结束语

本次试验让我们学习到了光的等厚干涉原理，利用这一原理我们学会了如何测量细丝的直径，使我们受益匪浅，实验过程中我们应当多次测量，因为实验过程中存在较大误差，应该仔细认真以免读数发生错误。

参考文献

《大学物理实验》张彦纯机械工业出版社《大学物理学》杜秀国白晓明机械工业出版社

范文三：利用激光衍射原理测细丝直径

河南科学No.5 Vol.30 第 30 卷第 5 期

2012 年 5 月 HENAN SCIENCE May 2012

文章编号:1004-391(82012)05-0568-03

利用激光衍射原理测细丝直径

李芳菊，耿森林

(渭南师范学院物理与电气工程学院，陕西渭南 71400)0

摘要:根据夫琅禾费衍射理论和巴比涅互补原理，推导出细丝直径的表达式，设计了用激光衍射法测细丝直径的

实验，由测量的数据，计算出了三种粗细不同细丝的直径，通过与其他传统方法比较，对于直径越小的细丝，此方法

具有测量精度高、非接触、无损伤的优点.

关键词:夫琅禾费衍射; 单缝衍射; 激光衍射; 巴俾涅原理

中图分类号:O 436,1文献标识码:A

Measurementof Fine)wireD iameter by Laser Diffraction

Li Fangju， Geng Senlin

(School of Physiscs and ElectronicEngineerin g，Weinan NormalUniversit yWeinan， 71400，0ShaanxiChi na) Abstract: According to the theory of Fraunhofer diffraction and Babinet principle，the fila mexpentr ession of diameteri s derived and the experiment which can measufrinee the)wi re diameters with laser diffracis tion designed. Based on measudatred a ，the fine )wire diameterswith three different thicknessare c alculated, The method，which was compared with tr aodittheriona l methods，has the advantages porfe chigh ision， non )contact and non)harm for thef ine)wires whose diameters wesmarllee r,

Key words: Fraunhoferdif fraction; singles lit diffraction; laserdif fraction; Babinetp rinciple

在工业生产和科学实验中，经常遇到尺寸小于1 mm的细丝直径的测量问题. 传统测量细丝直径的方法通常有两种:细丝称重法和游标卡尺或者螺旋测微器手工测量. 细丝称重法即就是将一定长度的细丝称重后，把丝细看成均匀细长的圆柱体，然后根据材料密度求出细丝直径. 但此方法的缺点是浪费材料、花费时间多、精度不高，而且不能测量细丝某一处的直径，是一种间接测量法. 游标卡尺或者螺旋测微器手工测量法具有测量方便、花费时间少的优点，但缺点是对于直径是微米数量级的细丝由于机械压力往往卡断细丝或者使细丝变形、测量误差大 . 一般的光学测量细丝直径的方法有:光学成像法、光学显微镜法等，如果采用

[1-3]一般的光学仪器测量，由于光的衍射现象，所以被测细丝越细，测量误差就越大. 而采用光学衍射测量法则可以达到精度高、速度快、非接触、无损伤、容易实现动态测量、使用方便且易于微机联接实现自动化测量等优点，在保证产品质量的同时，可以提高劳动生产效率. 因此，用光学衍射法测量细丝直径不失为一种有效的方法，且此测量方法在工业生产和科学实验中有重大意义、易于推广应用.

1巴比涅原理

如图 1 所示，若有两个衍射屏和， ??1 2

其中一个衍射屏的开孔部分与另一衍射屏的 + = 不透明部分准确对应，反之亦然，则称这对衍

射屏为互补屏 . 设 U(p)和 U(p)分别表示由 1 2 ? ? 12

图 1 互补屏 ?和?在观察平面上 p 点产生的衍射光场 .1 2

Complementaryshe ltering screnes Fig,1

收稿日期: 2012-03-21

基金项目: 陕西省教育厅项目(11JY051)9;渭南师范学院科研培育项目(11YKP014)

2 2 x + f ′ kλ 姨k d= ，(4x k

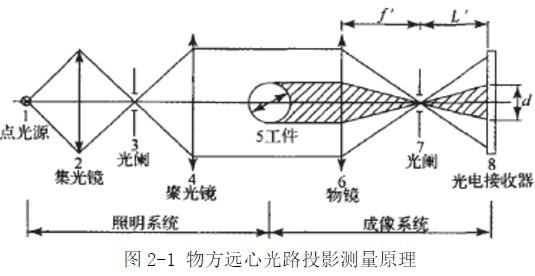
式中:x为 k 级暗条纹的位置;λ 为光波波长;f 为透镜焦距 . ′k

x平行激光束k d θ 被测细丝f ′

图 2 互补法测量细丝直径原理图

Fig,2 Sche me of using Babinet principle to measure the fine diameter

2 细丝直径测量及分析

生活中经常可见到直径小于 0,5 mm的细丝，实验中选取细导线里的小铜丝和直径小于0, 5 mm的铁丝

这两种材料无论在表面粗糙程度上还是在用途上都具有普遍性、代表面广、易测量的特点，所以选它们较为

6 -合理 . 选择了三种粗细不同的细丝，此外还有发丝 . 实验所用光源为 He)Ne激光，λ=632.8×10mm，透镜

焦距 f ′=400 mm . 其中，1 号细丝和发丝的测量结果如表 1:3 所示 .

1)1 号细丝

表 1 衍射法测量数据

Data measurde by diffraction method Tab,1 mm

测量次数及结果 ?1 级暗纹位置细丝直径误差1 2 3 4 5 6

x6.860 6.910 6.865 6.870 6.815 6.815 10.518 0.93% x5.860 5.895 5.870 5.905 5.850 5.890 -1

河南科学第 30 卷第 5 期 570 - -

表 2 螺旋测微器测量数据

Tab,2 Data measurd bye screw-threadm icrometer mm 测量次数及结果读数及 0 刻度修正细丝直径误差1 2 3 4 5 6

x 0.476 0.470 0.477 0.478 0.471 0.469 0.490 0.60% 0 刻度修正 -0.016 -0.020 -0.017 -0.016 -0.019 -0.015

2)发丝直径

激光衍射法测量发丝直径表 3

The diameter of a single measuredhair by laser diffraction Tab,3 mm

测量次数及结果 ?1 级暗纹位置细丝直径误差1 2 3 4 5 6

x5.845 5.844 5.854 5.805 5.803 5.844 10.068 0.03% x2.170 2.103 2.112 2.115 2.170 2.119 -1

衍射法测量效果及结论3

对 1 号:3 号细丝及发丝的测量结果经分析可知，在测量1 号、2 号、3号细丝的直径时，光的衍射法测量误差逐渐缩小(从 0,93,缩小到 0,03,)，而接触法或螺旋测微器的测量误差始终不变(保持在0,60,左右).

由此可得出:在光的相干性较好的条件下，细丝的直径越小，光的衍射法测量结果误差就越. 小当然，这种测量方法也有它的局限性 . 首先它只能用于测量很细的线径，一般在 0,5 mm以下，而且要求测量误差小，精度较高的场合 . 其次它需要相干性好、亮度高的光源. 尽管如此，衍射法测量细丝直径仍不失为一种有效的方法，它可以应用在在线加工中，测量结果可直接控制生产线，使细丝的直径受到自动控. 制这对目前电子工业中大量生产的金属细丝、光导纤维等有重要的意义.

参考文献:

,1,韩力，卢杰，李莉, 动态激光衍射法测细丝直径,J,, 物理实验，2006，26(4):12, -

,2, 苗润才，李芳菊，董军，等, 低频表面波对细激光束的衍射效应,J,, 光子学报，2007，36(5):877-880 ,

苗润才，朱峰, 激光衍射法测量液体薄膜厚度的研究,J,, 激光技术，2007，31(5):537539 ,-,3,

吕乃光. 傅里叶光学,M,, 2 版. 北京:机械工业出版社200，7, ,4,

(编辑张继学)

范文四：细丝直径的测量2

细丝直径的测量

班级：电气一班姓名：毛帅学号：140090106

摘要：

设计性实验是高校实验教学的重要内容, 其中最关键的环节是实验方案的设计。本文列举了细丝直径测量设计性实验的几种测量方案。本次设计性实验是：利用劈尖干涉测量自己的发丝直径。

劈尖干涉在生产生活中有很多应用，例如：利用劈尖干涉原理制成干涉膨胀仪，已测量样品的膨胀系数，用劈尖干涉测薄膜的厚度或者检查光学表面的平整度。

关键词：

细丝，膨胀系数，物理实验一、前言

利用劈尖干涉测量自己的发丝直径，根据薄膜干涉原理，用两个很平的玻璃板间产生一个很小的角度，就构成一个楔形空气薄膜，

用已知波长的单色光入射产生的干涉条纹，可以测量头发丝的直径。

二、实验原理

当两片很平的玻璃叠合在一起，并在其一端垫入细丝时，两玻璃片之间就形成空

气薄层（空气劈）。在单色光束垂直照射下，经劈上、下表面反射后两束反射光是相干的，干涉条纹将是间隔相等且平行于二玻璃交线的明暗交替的条纹。

相邻两暗纹（或明纹）对应的空气厚度

为干涉条纹总条纹

S 为相邻两暗条纹的间距，用读书显微镜测量（5次测量）

589. 3?10-6mm

Λ 为钠光波长，λ =

已知入射光波长λ，测出N 0和L , 就可计算出细丝（或薄片）的直径D 。

三、实验方法：

实验仪器：钠光灯读数显微镜劈尖装置

1、将细丝（或薄片）夹在劈尖两玻璃板的一端，另一端直接接触，形成空气劈尖。然后置于移测显微镜的载物平台上。

2、开启钠光灯，调节半反射镜使钠黄光充满整个视场。此时显微镜中的视场由暗变亮。

调节显微镜目镜焦距及叉丝方位和劈尖放置的方位。调显微镜物镜焦距看清干涉条纹，并使显微镜同移动方向与干涉条纹相垂直。

3、用显微镜测读出叉丝越过条暗条纹时的距离l, 可得到单位长度的条纹数

N 0。再测出两块玻璃接触处到细丝处的长度L. 重复测量五次，根据式

D =N 0L (λ/2) 计算细丝直径D 平均值和不确定度。

四、实验数据处理：

实验测量数据

单位（mm ）

L=35.40mm

D 平均=589.3*35.4*10-6/2*0.246=0.042 Us=0.147 Ud=0.025 S 平均=0.246 Ur=1.9%

五、结束语

经上网查证，人头发丝一般是0.05-0.07mm 之间，与实验数据相差不大，说明本次试验比较成功。实验中可能会存在误差，测量误差，读数误差。偶然误差等等。排除这些误差，实验相对会可以精确。

六、参考文献

[1].汪晓元. 大学物理教程. 北京邮电大学出版社,2005,162～164

[2]姜华，一种测量金属细丝直径的新方法[J]，青海大学学报（自然科学版），2006

[3]高鹏，物理设计性试验研究[J].中国电力教育，2006

范文五：劈尖干涉测细丝直径中测量点的选择

1003 , 1251( 201034) , 0035 , 03: 文章编号

劈尖干涉测细丝直径中测量点的选择

,曲铁平李凤岐

( ,110159)沈阳理工大学理学院辽宁沈阳

摘要: 劈尖干涉测量细丝直径,采用钠光灯作为光源。实验中,干涉条纹的清晰度随

; ,测量点的变化而变化将空气劈尖的等厚干涉原理与干涉条纹的反衬度相结合研究劈

。,尖干涉条纹清晰度的变化原因结果表明测量点应选在劈尖棱边干涉级次较低的位 ( n , 100) 。置级次

: ; ; ; 关键词劈尖干涉细丝直径干涉条纹的反衬度测量点

:O436.1 :A 中图分类号文献标志码

Seleciton of Measurement Point for Determining Filament Diameter by Wedge

QU Tieping,LI Fengqi

( ShenyangLigo ng Univeirtsy ,Shenyang 11015,Chi9na )

Abstract: The reason why the clarityo f w edgien terference fringes varied at differentp osi- tions w as explained with equal thicknesisn terference principleo f air w edge and contraosf t interference fringes( It w as pointed out that the measurement point shouldbe selectednear the

edge of w edeg,w here thein terference order w as low (

Key words: w edgein terferenc; efilament diameter; contrast; measurempoentint

利用劈尖干涉测定细丝直径作为等厚干涉的

,。具体应用是一项很好的设计性实验由于此试 1 实验原理及方法

,验可以加深对等厚干涉理论的理解培养

,: 综合能力因而很多学者对此实验及其实际应用空气劈尖用两块光学平板玻璃组成将两块 ,1 , 5,。进行了系统研究劈尖干涉实验通常采用钠 ,,光学平板玻璃叠在一起一端插入一细丝在两玻

,。光灯为光源条纹的清晰度随测量点不同会发生璃板间形成空气劈尖 ,6,,,待测细丝直径为明显变化影响测量精度但对这一现象的解释还

。未见报导本文用干涉条纹的反衬度对这一现象 L n??Δλ D = 2l ,,进行理论分析指出测量点的合适位置对劈尖干

: L ; n 式中为棱边到细丝处的总长度Δ为记录的 ,涉实验具有指导作用并为研究钠光干涉提供

; l n 。条纹数为 Δ条干涉条纹对应的间距。参考

用钠光灯作为光源,通过 JXD-250 型读数显

2013 , 08 , 28: 收稿日期

: ( 1960—) ,,,: (作者简介曲铁平男副教授研究方向基础数学与物理实验

36 沈阳理工大学学报33 第卷

,,微镜观察干涉条纹用数码相机拍摄不同级次的干涉条纹的叠加导致不同级次的条纹清晰度不

干涉条纹图像。同。 ,7,劈尖干涉光程差近似为

2 结果及讨论 λ δ = 2d + 2

式中,λ 为入射光波长,d 为干涉条纹所在处对应干涉级次 n 分别为 20、180 及 350 各级干涉

的劈尖厚度。当 δ = ( 2k + 1 ) λ/ 2 ( k = 0,1,2, 1 。条纹的数码照片如图所示

…) 时,形成第 k 级暗条纹,其对应的劈尖厚度为

d =k /2。λ

,由于钠光的两条谱线波长 λ?λ因而二者的1 2

( 2d = k= k) ,干涉条纹除特殊点 λλ外不重叠导1 1 2 2

d 。致干涉条纹的反衬度随劈尖厚度而变化

,8,干涉条纹的反衬度

I, I ma x minE = I+ I ma xmin

: I; I; 式中为光强极大值为光强极小值反衬 ma xmin

度 E 反映的是干涉条纹的清晰度,其值介于 0 , 1

之间,E 越大条纹越清晰。

劈尖干涉测量细丝直径实验中,劈尖厚度为

d ,( ) 时波长为 λ与其对应的角频率为 ω的谱线 1 1 ,7,产生的两相干光的位相差为

4 dπ = 1 λ 1

A sin( t) ,令劈尖上表面反射光为 ω则下表面 1

反射光为 A sin( ωt + ) ,二者干涉后结果为 1 1

X= Asin( ωt) +A sin( ωt + ) = 2Asin( ωt + 1 1 1 1 1

/2) cos( /2) =A sin( ωt + /2) 1 1 1 1 1

其振幅 A = 2A cos( /2) 1 1

1 2 2 2 =A = 4A cosI光强 1 1 2

,同理对波长为 λ的谱线有 2

4 dπ = 2 λ 2

2 2 21 图不同级次干涉条纹的数码照片 I = 4A cos2 2

1 ,图显示不同级次干涉条纹的清晰度发生 ,为简化计算上述推导中已假定两条谱线的明显变化: 级次 n = 20 附近的条纹非常清晰,级次 A ( 与实际情况基本相符) 。反射光振幅皆为

n = 350 ,n = 180 附近的条纹非常模糊而级次附近的,7,,,由于 λ ? λ 两条谱线之间无干涉总光 1 2 。条纹的清晰度介于前二者之间出现这一变化的强 I 应为二者各自干涉后光强的线性叠加。

, 根本原因是钠光灯所发光并非严格的单色光而 2 1 2 2 2 I = I+ I= 4A cos +c os =1 2 ,是包含波长非常接近的两条谱线其波长分别，， 2 2 = 589. 0nm = 589.6 nm。为 λ和 λ通过劈尖干涉形1 2 1 1 2 ( 1 +c os) + ( 1 +c os) 4A =1 2 , , 成的干涉条纹是这两个不同波长的谱线形成的 2 2

3 : 37 第期曲铁平等劈尖干涉测细丝直径中测量点的选择

+ , dE 2 1 2 1 2 的增大 , 的绝对值增大。这一结论与干涉Δ4A 1 + cos cos = ，， dΔ 2 2

n 20、180 350 级次分别为及级干涉条纹的数码 Δ 2 Δ + 4A 1 +c os cos 2 , , ，， 2 2 。照片所显示的结果完全一致

4( , ) dπλλn 0 491 , 由于当级次由逐渐增加到时反衬 2 1 = , =,式中 Δ 是劈尖厚度为 1 2 λ λ1 2 E 1 0,度由逐渐减小到对应的干涉条纹由清晰

d 时两不同波长钠光各自对应的位相差的差值。 ,逐渐变为完全消失所以测量点应选在劈尖棱边

λ 21。一端 983 , 1,,d = ?故随的变化速度由于 2 , Δ λλ 1 2

,I d 远大于 Δ 的对应值因而总光强随变化的部 3 结论 ΔΔΔ 2 + + cos 4Acos cos 是以分调 2 2 ，，，，，， 2 2 2 ,利用劈尖测量细丝直径时劈尖棱边干涉条 Δ 2 1 +cos ,,I= 4A幅的余弦函数其最大值 1,; 纹级次较低的位置反衬度约为条纹最清晰当 ma x ，， 2

350( 干涉级次增加到对应空气薄膜厚度为 2 Δ1 ,,I= 4Acos 其反衬度为最小值 min ，， 0. 1031mm) 4364,,0. 时反衬度已减小到条纹变 2

。( 得非常模糊因而测量点应选在棱边附近级次 I, I ma x minE = = n , 100) ,。避免选在待测细丝附近 I+ I ma xmin

Δ Δ 2 2 4A1 +cos cos ,4A1 , ，，，， 22 Δ :参考文献 = cos Δ 2 2 Δ 2 cos cos 4A1 ++4A1 ,，，，， 2 2 ,1, ,,,( 张兰霞解顺强王冀霞等劈尖干涉实验的误差分 1 不同级次干涉条纹反衬度的理论值如表所 ,J,( ( ) ,2009,12:析及改进中国校外教育基教版示( 取 λ = 589. 3nm。) 147 , 148(

1,2, ( ,J,( 表不同级次干涉条纹的反衬度刘金龙劈尖干涉条纹定域的解析研究物理与

,2008,18( 4) : 54 , 57( 工程 Δn d / mm E

,3, ,,,( 张国林唐军杰邵长金等劈尖干涉条纹变形原因 0 0 0 1 , 320 0. 040730. 9980 π 5. 893 ×10 ,J,( ,2003,16( 2) : 14 , 16(的研究大学物理实验 , 20. 3666180 π 0. 8387 5. 304 ×10 ,4, ,,( 冯颖宋瑞丽王连加利用劈尖干涉测定细丝直径的实 350 0. 4364 0. 1031 0. 7125π 491 0 0. 1447 ,J,( ,2003,23( 2) : 46 , 49(验研究东北电力学院学报 π ,5, ,,( 花世群骆英洪云基于等厚干涉原理的液体折射

,J,( ,2006,3( 31 1 ) : 1542 ,率测量方法中国激光 , 1 ,,n 0从表可以看出当 Δ π 时随级次由 1546(

491,d 0 逐渐增加到相应的劈尖空气薄膜厚度由 ,6, ( ,M,( : ,李志超大学物理实验北京高等教育出版杜 0. 1447mm; 0 ,逐渐增加到 Δ 由逐渐增加到 π干 2001(

E 1 0,n 涉条纹的反衬度则由逐渐减小到且随着 ,7, ,( ,M,( : ,母国光战之令光学北京人民教育出版社

1979( ,E 。E 的增加的减小速度越来越快这是由于随

,8, ,( ,M,( : 吴强郭光灿光学合肥中国科学技术大学出 Δ 的变化率为

,2003( 版社 dE 1 Δ = , sin dΔ 2 2 ( : ) 责任编辑赵丽琴 dE 00,, 当 ?Δ ?π 时小于或等于且随着 dΔ

转载请注明出处范文大全网 » 利用等厚干涉测金属细丝的直径