答案:B.
解析:由于乘法与除法是同级运算,所以运算顺序从左往右依次进行.()·()÷(-)=()·()·=-.故选B.
2.(-)2n的值是( ).
A. B.- C. D.-
考查目的:分式的乘方及幂的乘方、积的乘方运算法则.
答案:C.
解析:∵是偶数,∴.故选C.
3.如果()2÷()2=3,那么8 4等于( ).
A.6 B.9 C.12 D.81
考查目的:分式的乘方、除法混合运算及代数式的求值等相关知识.
答案:B.
解析:∵
B.
二、填空题 =3,∴.选
4.一箱苹果价的 倍.(用含千克,售价元;一箱梨子千克,售价、的代数式表示) 元,?则苹果的单价是梨子单考查目的:重点考查运用分式的除法解决实际问题能力. 答案:. 解析:由题意可知苹果的单价是元/千克,梨子的单价是元/千克,则苹果的单价是梨子单价的倍.
5.化简()2·()·()3的结果为 .
考查目的:重点考查分式的乘方与分式的乘法混合运算能力.
答案:.
解析:.
6.计算()2÷()·(- )3的结果为 .
考查目的:重点考查分式的乘方与分式的乘除法混合运算能力.
答案:.
解析:.
三、专心解一解(解答应写出文字说明、演算步骤或证明过程)
7.计算:÷·;
考查目的:重点考查分式的乘除法混合运算能力.
答案:.
解析:. 8.先化简求值. ÷[()·()],再任选一对你喜欢的、的值代入考查目的:重点考查分式的乘除法混合运算能力.
答案:化简结果为,求值结果不唯一.
解析:
取值时要注意
≠0,≠0,≠0,≠0.否则算式无意义. .
分式的乘方乘除加减混合运算
能掌握分式?乘方的运算?法则,能运用分式?的乘除、乘方法则进?行混合运算?。
经历分式乘?方的法则的?推导过程,理解乘方与?乘法的关系?,体会混合运?算的算理
进一步培养?学生观察、类比、讨论、交流、化归的数学?思想,感受知识的?应用价值。
理解并掌握?乘方的法则?,并应用于分?式的运算中?。
对分式乘方?法则的理解?。
活动流程 活动内容和?目的 (一)激情导学 通过小测达到两个目的?,一是温习旧?知识,?
通过两题加减混合运算?题的检测,归?二是渗透本节课要探究?的分式混合?运算内?纳出分式加减混合运?算的算理和?方法? 容,来观察学生的自主学习?的表现。?
充分应用知识迁移,归纳出分式?乘方法则,?(二)合作探究 培养学生的自主探究,善于应用旧?知识进行?
探究分式乘方的法?则 拓展延伸,以及交流意?识?
以老师的讲带动学生的?思维,达到师生互??
动的目的。
(三)启思点拨 学生归纳总结本节课的?主要内容,交流在探?
一讲一练,通过例题,掌握方法 索混合运算的?过程中的心?得体会,不断?积累
数学活动经验??,教师通过作业了解学生?学习?(四)差异评价 情况,调整下一步的教学。?
提问的方式?,让学生进一步加深本节?所?
学内容。
分式乘除乘问题与情境方混合运算? ?题。(课堂小测)。(放课件)?师生行为 设计意图
教师组织学生?通过小测达到?
小测,测后学两个目的,一?
生同桌互改,?是温习旧知?
然后请部分学?识;二是渗透学生做完后?思考以下问题(课件展示)? 生上讲台?板本节课要探究??(1)分式乘除混合运算的基?本步骤是什?么,? 演,老师与学的分式混合运?(2)在分式的乘除混合运算?中,应该注意些?什么,? 生共同?纠正,算内容,来观(3)怎样的结果才是最简的?结果,? 并通过小测温?察学生自主学?
故知新,重点习的表现。?
谈一谈混合运?
算的方法。? 我们学过乘?方的意义以及分式乘法?的法则,下面我们根?? 据乘方的意义和分式乘?法法则填空?(课件展示)? 教师提出上面?通过一组精心?
问题后并板?设计的填空?
书,巡视、观题,让学生应
察学生的思维?用所学知识,?
动态,适时启发现并归纳总?
发学生,并引?结出分式乘方?
导学生归纳出?的法则,进一?
乘方的法则。? 步培养学生自?
学生思考上述?主探究,善于?n个 问题,充分利应用旧知识进?
用知识迁移,?行拓展延伸,?
即乘法法则推?以及交流意?
导出结论,然?识。
后与同伴共同?
合作,归纳出
分式乘方法则?
是分式乘方要??
把分子、分母请一个同学?来总结一下上面的规律?:(老师板?分别乘方。? 书) 老师引导:通
俗的记忆“?商
的乘方等于乘?
方的商”?。 例1:计算 以教师的
讲带动学生的??巩固:计算: 思维,达到师
生互动的目?
教师引导学生?的。
分析例题(?1)由浅深入的练?
(2)(3),习,进一步帮
启发引导学生?助学生理清在??例2:计算 通过例题,掌?运算过程中需?
握方法(板演要注意的地?
过程) 方,提高学生巩固:计算 学生参与的计算能力。?
教师的分析,?通过练习,教
不断向教师提?师及时了解学?
出问题,从而生对本节知识?
归纳出运算方?掌握情况,对?
法和注意点。? 教学进度和方?例3:计算: 练习巩固题,?法进行调整,?
学生演板,其并对有困难的?
余学生都独立?学生给以个别?
练习,在学生指导。
练习的过程?让学生经历运?巩固:计算: 中,教师要深用知识解决问?
入小组帮助和??题的过程,给?
指导学生。 学生获得成功?
的体验,激发?
学生的学习兴?
趣。 小结布置作业? 教师通过提问?以期获得学生?作业:课本第22页第?3题。 的方式让学生?的反馈信息,?
巩固本节所学?作为后面教学?
内容,加深印?进度和方法适?
象,布置作业,当调整的依据?
学生课后独立?
完成。
分式的乘方,乘除,加减混合运算
分式的乘方,乘除,加减混合运算
课型:新授 班级:_______________ 姓名:________________ [学习目标] 1、熟练掌握异分母的通分运算;
2、掌握异分母分式加减乘除法的法则,并会运用法则进行异分母分式加减乘除法的计算。 3、能够掌握分式加减乘除乘方法则来解决混合运算的实际问题。
[学习重点]能分析运算顺序, 并能熟练地运用各种法则进行分式的混合运算。 [学习难点]分母是多项式的分式的混合运算
学习过程] [
一、预习看书21--22页,自学例题8并做好练习题
二、完成下列练习:
1、式与数有相同的混合运算顺序,先______再________最后______;同一级运算,则应该________________;有括号,可先________________;也可运用运算律等简化运算。
11132、计算 (,,),x32xxx
方法一:原式= [通分] 方法二:原式= (乘法分配律)
三、基础训练:,先独立思考,再合作交流,展示讲解。,
4、 见教材27页第6题
5、 见学习指要第4页3训练一3题、训练二1、2、3、
你预习后还存在的问题:__________________________________________________
_______________________________________________________________________
小组评价:_________________________________________组长签字:________ 四、合作探究,解决问题:
22x2x,3xy,2y,,4、已知:求的值是( ) 22y72x,3xy,7y
284207A B C D 103103103103
11x,y,(,x,y)3、计算: (思考怎样做会更快更简单) 2xx,y2x
五、达标检测:
6、阅读理解:
1
a,21,21,aa,1
,,,,a,2a,1,, ,,,,,,,,a,1a,11,aa,1
,,,,,a,2,a,1
,,1
(,) 上述计算过程中,从_______步开始出现错误;
(,) 错误的原因是___________________________________________________;
(,) 本题正确解法是:_______________________________________________
222,,2x,1yy,,2,,(1,),7、计算:(1) (2) ,,,,2,,x,1x,16x4x,,,,
25222xxx96aba2a,,,,,(3)、 (4)、 ,,,,,,,,,322bx3x3x5b2ab,,,,,,
六、学习后的的评价:
小结本节课你学到了什么:
异分母分式的加减法法则:
一般步骤:
注意事项:
你自己对本节学习后的评价_____________(很好、较好、一般、差)
理由:_________________________________________________________________
小组评价:_________________________教师评价:___________________________
2
分式的乘方,乘除,加减混合运算
分式的乘方,乘除,加减混合运算
[学习目标] 1、会异分母的通分运算;
2、牢记异分母分式加减乘除法的法则,并会运用法则进行异分母分式加减乘除法的计算。 3、会用分式加减乘除乘方法则来解决混合运算的实际问题。
[学习重点]能分析运算顺序, 并能熟练地运用各种法则进行分式的混合运算。 [学习难点]分母是多项式的分式的混合运算
[学习过程]
一、预习看书21--22页,自学例题8并做好练习题
二、完成下列练习:
1、式与数有相同的混合运算顺序,先______再________最后______;同一级运算,则应该________________;有括号,可先________________;也可运用运算律等简化运算。
11132、计算 (,,),x32xxx
方法一:原式= [通分] 方法二:原式= (乘法分配律)
三、基础训练:,先独立思考,再合作交流,展示讲解。,
4、 见教材27页第6题
5、 见学习指要第4页3训练一3题、训练二1、2、3、
你预习后还存在的问题:__________________________________________________
_______________________________________________________________________
小组评价:_________________________________________组长签字:________ 四、合作探究,解决问题:
22x2x,3xy,2y,,4、已知:求的值是( ) 22y72x,3xy,7y
284207A B C D 103103103103
11x,y,(,x,y)3、计算: (思考怎样做会更快更简单) 2xx,y2x
五、达标检测:
6、阅读理解:
1
a,21,21,aa,1
,,,,a,2a,1,, ,,,,,,,,a,1a,11,aa,1
,,,,,a,2,a,1
,,1
(,) 上述计算过程中,从_______步开始出现错误;
(,) 错误的原因是___________________________________________________;
(,) 本题正确解法是:_______________________________________________
222,,2x,1yy,,2,,(1,),7、计算:(1) (2) ,,,,2,,x,1x,16x4x,,,,
25222xxx96aba2a,,,,,(3)、 (4)、 ,,,,,,,,,322bx3x3x5b2ab,,,,,,
六、学习后的的评价:
小结本节课你学到了什么:
异分母分式的加减法法则:
一般步骤:
课堂感悟:
2
分式的乘方
编写人:王丽卿 审核领导:王秋芬
学习目标
1、牢记分式乘方的运算法则,并能根据此法则进行熟练无误地运算。 、通过分析、归纳,自己总结分式乘方规律,培养分析归纳能力。 2
教学分析
重点:准确熟练地进行分式的乘方运算。
难点:准确熟练地进行分式的乘方运算。
教学过程
一、复习
n1(首先复习整式乘方的概念:a是什么意思,a表示什么,n表示什么,
mnm+nmnmnnnn2(再复习乘方运算的性质:aa=a;(a)=a;(ab)=ab(接着提出问
板书课题() 的内容:分式的乘方((
3(复习分数的乘方法则,
4(最后复习分式乘法法则。
二、新授
1(由乘方的定义和分式乘法法则得到:
注意:其中a表示分式的分子,b表示分式的分母,且b?0( 2(总结乘方法则:分式的乘方,等于把分式的分子、分母各自乘方,写成公式是:(可用小黑板或投影仪显示)
3(自学例题:
3
222nnn注意:分母(3y)=3?y,用到了整式乘方运算性质:(ab)=ab( 在此例中:根据分式的符号法则,可以把分母中的符号移到分式前,再按(-1)的奇次方为负,偶次方为正来确定符号,这里仍应指出乘方运算的性质: mnmn(a)=a(
此例提醒学生注意符号及约分(做完后,提问:若x=2、y?0,或x=2、y=0,或x=0、y=1时,原式的值是多少,很可能学生答为-32,-32,0(此时必须指明:第一个结果是正确的;第二个、第三个结果是错误的,因为分式的大前提是分母不为零(这样可以加深学生对分式概念的理解(
三、练习
课后练习(找四名学生到前面板演,其他学生在下面做练习() 四、小结
1(重述分式乘方法则(
2(分式的分子或分母带符号的n次方,可按分式符号法则,变成整个分式的符号,然后再按-1的偶次方为正、奇次方为负来处理(当然,简单的分式之分子分母可直接乘方(
3(注意熟练、准确运用乘方运算法则及分式乘除法法则(
4(注意混合运算中应先算括号,再算乘方,然后乘除,最后算加减( 测试:习题A:7、B:3、4。及基础训练:同步练习。
课后感:
4
分式的乘方及乘除混合运算
第2课时 分式的乘方及乘除混合运算
要点感知1 分式的乘除混合运算,先将除法统一为______,然后再计算.
预习练习1-1 计算:
2x 3x ÷2. . x -2x -4x +2
a n a n
要点感知2 分式的乘方是把分子、分母分别_____.即() =n ,其中n 是正整数. b b
2x 2
2-y 23) =_____,() =_____. 预习练习2-1 计算:(3y 2x 3
要点感知3 分式的乘方、乘除混合运算,应先_____,再_____.要注意先确定运算结果的符号,以及乘除同级运算顺序是_____.
x 2-y y 2÷.() 的结果是( ) 预习练习3-1 计算y x x
A.-x x 2
B.- y y C. x x 2D. y
知识点1 分式的乘除混合运算
1. 计算: 2x 2y 5m 2n 5xym . ÷(1); 3mn 24xy 23n
(3)(2)a +2a -11. ÷; a 2-1a 2+4a +4a +23x 2x ÷. ; 4x -316x 2-94x +3 (4)1x -1÷(x +2). . x -1x +2
知识点2 分式的乘方运算
2. 计算: y 2(1)(-) ; x 2 2a 2b 3(2)() ; c 5ab 33(3)() . -3c 2
知识点3 分式的乘方、乘除的混合运算
m 2-n 2n -m 2m +n .() ÷(2); 2(m -n ) nm m x 2-y 22x 3) ÷(x +y ) 2.() . (3)(xy x -y 3. 计算: 13b 2b (1)(-) ÷(-2) 3÷() ; ab 2a a
4. 下列分式运算,正确的是( )
m 4n 3m A. 5. 3= n m n
5. 计算1÷3x 33x 3B. () = 3 4y 4y 2a 24a 2C. ( ) =22a -b a -b D. a c ad ÷= b d bc 1+m 2.(m-1) 的结果是( ) 1-m
B.-m 2+2m-1 C.m 2-2m-1 D.m 2-1 A.-m 2-2m-1
6. 计算:4a 2b ÷(
7. 计算: 2a 2a ) ·3=_____. b b
2x +y 2x +y 2xy 326x 2a 2a 3x -22x 2-44÷) ÷3; (2)(-) ·(-) ÷(-ab); (3)(1)() ÷2. ·(x-y); (4)(x -y x 2-2xy +y 2-z 2y b b x x +2x
x 2-1x +11-x 8. 计算:2,下列解答过程是否正确?若正确,请写出每一步的依据;若不正确,请指出错÷. x -2x +1x -1x +1
误的原因,并纠正.
解:原式=
(x +1)(x -1) x +1÷(-1) =. (x -1) 21-x
1122ab 23ab 3229. 先化简,再求值:() ÷(2) a=-b=. ·[],其,2(a -b ) 23a +b a -b 2
10. 小明在做一道化简求值题:
x 2-2xy +y 2x -y . 2, 他不小心把条件x 的值抄丢了,只抄了y =-5,你说他能算出这道题的正确结果吗?(xy-x) ÷xy x 2
为什么?
word 版习题
b 4a 3+ab 2-2a 2b b 2-a 2
. ÷11. 已知a +10a+25与|b-3|互为相反数,求代数式232的值. (a -b ) b ab +b 2
挑战自我
x 4+112. 已知x -5x+1=0,求的值. 2x 2
参考答案
要点感知1 乘法
预习练习1-1 2x 2
. 3
要点感知2 乘方
预习练习2-1 4x 4y 6
-9 9y 28x
要点感知3 乘方 乘除 从左至右
预习练习3-1 A
11x 1m -n 3x 2y 48a 6b 3125a 3b 9a 8b 2
1.(1).(2).(3).(4).2.(1).(2).(3).3.(1).(2).(3). -2y 2(x +2) 2xy 2-y 3a +1mn 22x 2c 327c 62
4.D 5.B 6.a a x -21-x 2y 9
7.(1)4.(2)-9.(3)(x-y)2.(4).8. 不正确,正确答案为. 9.-6. b x x +13z
10. 原式=-y.∵分式的值与x 的值无关,∴他能算出这道题的正确结果,是5. 11.-
45. 12.23. 8
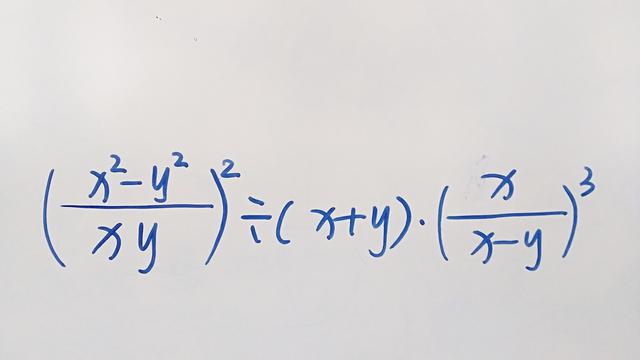
转载请注明出处范文大全网 » 分式的乘除及乘方混合运算



 蜜蜂家的超粉
蜜蜂家的超粉

